基于全线程树数据结构的笛卡尔网格高效生成技术

陈浩，毕林，华如豪，周清清，唐志共，袁先旭,*

1.中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000

2.中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

随着CFD在工程实际中的深入应用，模拟中所面临的的几何外形也越来越复杂。在CFD计算中，网格生成需要频繁的人机交互，并且生成的网格质量严重依赖用户经验。有研究表明，网格生成过程占据了CFD周期中总用时的70%以上，是制约CFD效率的主要瓶颈。如何减少网格生成人工干预，提高高质量网格生成自动化水平，成为当前网格技术领域的研究热点之一。

通常使用的网格大体上分为3类：贴体结构和非结构，以及非贴体的笛卡尔网格。贴体结构网格利于附面层特征的模拟，具有较高的质量，但针对复杂外形生成要分多块进行，要考虑不同块之间的过渡是否光滑。这在拓扑结构复杂时不易生成，即使是对网格生成有经验的人员，仍然需要大量的时间。非结构网格与之相比，生成难度降低，自动化程度提高，但是黏性特征的捕捉能力却不足，并且非结构网格还存在存储量较大、不利于高阶高精度格式应用的限制。笛卡尔网格方法相对前两种方法，可以完全自动化生成，而且其自适应加密和粗化十分方便，使得网格的质量较好，能够较准确地捕捉流动结构特征。因此，自适应笛卡尔网格方法吸引了很多学者关注。

但是笛卡尔网格方法也有其不足，它的非贴体特性导致在与壁面相交处会产生大小、形状差异比较大的单元，从而为壁面附近的高精度模拟带来不便。为了降低这种不足带来的负面影响，尤其是对于黏性流动模拟，一般采用混合网格方法、切割或融合网格方法以及浸入边界方法等壁面处理方式。其中，前两者实际上是把非贴体的壁面网格转换成贴体的形式，提供了一种可行的选择，但是其壁面处理的难度也大大增加，降低了笛卡尔网格的灵活性。很多学者采用具备简单性和灵活性的浸入边界方法，并通过提高壁面网格加密程度或借助于壁面函数的方式，提高黏性流动的模拟精度。

此外，为了方便自适应，笛卡尔网格通常采用四叉树或八叉树数据结构。虽然这种数据结构存储量较少，但很多信息需要通过临时计算的方式获取，从而导致计算量较大。如果采用非结构网格的数据结构，虽然方便调用网格信息，但存储量会较大。Khokhlov提出的全线程树数据结构给出了一种较好的选择，其在叉树数据结构的基础上充分利用闲置的内存节点，重新组织网格的存储信息和连接方式，方便相邻单元的检索，以减少计算量。但目前其尚未得到推广应用，需要进一步发展。

通常，在相同的模拟精度时，笛卡尔网格量会明显高于贴体结构网格的数目。对于复杂外形的流动模拟，尤其是在非定常情况下，网格量会进一步增加，从而更加凸显笛卡尔网格面临的计算量和存储量的问题，使得网格生成耗时明显增加，不可忽略。很多学者通过大规模并行技术来应对上述难题，但是高性能计算平台并未普及，研究人员仍然需要在个人计算机上完成CFD数值模拟工作。

针对以上问题，有必要构建一种高效的三维自适应笛卡尔网格生成方法，减少大规模网格量时的网格生成时间，以提高笛卡尔网格方法对复杂外形和复杂流动问题的实用性。

1 自适应笛卡尔网格生成流程

自适应笛卡尔网格的加密方式主要分为两种：各向同性和各向异性，本文讨论的是各向同性的方式，即在三维情况下，网格被分割成8个相同的子单元。为了提高网格的生成效率，本文发展或应用了很多技术方法，如采用全线程树的笛卡尔网格数据结构、基于KD树的物面数据结构、辅助判断网格类型的染色算法等，具体的生成流程如下：

读取基于STL(STereo Lithography)格式的外形数据文件，构造物面离散三角形网格的KD树，方便后续步骤快速检索。

根据外形的几何尺寸设定计算域，并设定网格步长，划分均匀的初始离散网格。

通过FTT数据结构建立笛卡尔网格的信息存储和网格间的连接方式。

判断笛卡尔网格与物面的相交关系。

通过射线相交方法，结合染色算法，判断笛卡尔网格相对物面的位置关系(内部或者外部)。

将与物面相交的笛卡尔网格单元进行一定次数的加密，并将曲率变化较大的位置进一步加密，直至网格的密度达到了能够准确描述几何外形特征的程度。

对于分割得到的新出现的网格，通过步骤4和步骤5判断网格与物面相交与否，以及网格中心点相对物面的位置。

判断新出现的网格与相邻单元的层次差是否小于1，对不满足的邻居单元进行加密，确保网格的质量。

进行一定步数的计算，根据流场解特征进一步自适应，并重复步骤8。

2 笛卡尔网格数据结构

笛卡尔网格的数据结构主要分为3种：结构式、非结构式和叉树式，为了便于自适应操作和节省内存存储，一般采用叉树结构居多。叉树数据结构本质上是一种分层式数据结构，不同层之间的划分依据是网格的大小，而决定网格位置的是其所处的上一层单元，也就是父单元，同样的，该单元也可以作为父单元划分得到数个子单元,叉树不同层级的父子单元通过指针建立访问和联系的方式。由于本文工作针对三维外形，所以以八叉树为例，如图1所示。

图1 基于八叉树数据结构的网格分割Fig.1 Cell subdivision using octree data structure

采用叉树数据结构的优势之一是自适应的易操作性，但也有不足之处，就是网格信息查询和调用的计算量偏大。例如，网格单元的相邻单元没有预先存储，需要在调用的时候，通过查询算法获得。此外，叉树结构的存储也存在一定的内存浪费，因为叶子节点的网格单元，其分配的子单元指针并没有指向，实际上是闲置的，在网格规模很大时，这部分浪费的内存不容忽视。针对上述不足，Khokhlov提出了全线程树数据结构(Fully Threaded Tree，FTT)。这种数据结构是传统的叉树数据结构的改进版本,它将叉树数据结构中叶子节点闲置的指针利用起来，指向邻居单元的父单元，从而构建快速访问邻居单元的“线程”。

FTT在最初提出时，限于当时的硬件水平，存储信息较少。在本文工作中，通过增加关键信息的存储，对该数据结构进行改进，以减少网格生成过程中的计算量，进而提高效率。

本文选择存储的信息是与空间网格单元相交的各个物面网格单元的序号，其对网格生成的效率有着重要影响。自适应网格生成过程中一个计算量很大的操作是判断网格是否与物面相交。传统的方式中，网格类型判断过程中父和子单元是独立判断的，使得空间网格单元与各个物面单元间相交信息需要重复计算。事实上，与子单元相交的物面网格肯定与父单元相交，遵循这个规律，如果能把与父单元相交物面进行动态存储，那么子单元再进行相交判断时候只需要在与父单元相交的网格面这样一个较小的范围内进行搜索，能够极大地降低计算量，从而提高网格单元类型判断和自适应生成的效率。

基于上述思路，利用FTT按照如图2所示方式构建数据结构。图中，父单元-子单元、子单元-父单元以及邻居单元-邻居单元之间的指针分别用不同颜色的箭头表示，通过Oct来组织，每个Oct包含8个单元。每个单元有一个与之关联的物理状态矢量，以及一个指向包含其子单元的Oct指针，如果没有的话，指向NULL。每个Oct包含网格单元的层次OctLv、网格中心点坐标(,,)、指向父单元的指针OctPr以及指向各个方向邻居的父单元的指针数组OctNb(6)。本文增加了存储与网格单元相交的各个物面网格单元的序号的动态数组OctTC(∶)。所有单元存在目标空间网格单元相交的物面网格单元时，动态数组就会被分配内存，并将所有相交物面网格单元的序号逐个存储。在完成子单元的计算后，父单元的存储数组会被释放内存。

图2 全线程数据结构中单元和Oct的关系Fig.2 Relationship between cells and Oct in FTT

大体上来说，采用传统的邻居单元查找方式平均遍历的树层数约为2，而如果采用FTT结构，平均遍历层数则约为1/2，在搜索邻居的时间上可以节省大约75%。在内存占用方面，采用传统的叉树数据结构，要存储完上述信息，每个单元需要8 words的内存，采用FTT方式，每个单元需要2 words的内存，相对于传统方式明显降低。

由于增加了相交信息的存储，每个单元内存占用会有所增加。当物面离散网格数目为，空间网格数目为，在考虑相邻单元对于相交物面的重复记数的情况下，由相交信息存储所引起的平均每个Oct的内存增加量约为2/words，或者每个单元的内存增加量约为/(4) words。排除极特殊的情况，一般空间网格量明显多于物面网格数，即/，所以平均每个单元的内存增加不大于1/4 words，整体上的内存占用仍然在一个较低的水平。

3 初始网格生成

在进行流动计算前，首先需要根据几何外形的尺寸设定计算域。根据数据文件里几何构型各个离散面元的信息，可以确定所有面元各个顶点坐标的最小和最大值，从而建立几何最小的方形包围盒[(,,), (,,)]，如图3所示。计算域[(,,), (,,)]应完全包含整个几何外形。

图3 计算域和几何包围盒Fig.3 Computational domain and geometry bounding box

计算域的大小设定除了需要考虑几何尺寸外，还有来流的情形和流场的结构特点，这就得根据具体情况设定。需要说明的是，本文工作是针对封闭的几何外形计算外部流动的问题，其他情况(如圆管流动)的网格生成方法与本文的工作原理类似。

在完成上述工作之后，就可以划分初始的计算网格。首先需要确定大小合适的初始网格尺寸，既需要保证基本的流动分辨率，又不能太小导致初始网格量太大。这里对计算域均匀离散：

(,,)=(,,)

(1)

式中：、、为3个坐标轴方向的离散单元尺寸，为设定的初始网格边长。

沿笛卡尔坐标轴各个方向的网格数目分别为

(2)

式中：、、分别是沿各个坐标轴方向计算域的长度。

4 网格类型判断

对于本文的笛卡尔网格生成技术而言，很重要的一项工作是判断网格类型。按照网格中心点对于封闭的物面的位置(内部或外部)，分为物体外部网格点和物体内部网格点。按照相交关系，又分为物面相交单元、物面内部单元和物面外部单元。这是后续进行网格自适应生成和浸入边界处理的基础。

4.1 判断网格点类型

4.1.1 射线相交方法

在建立几何包围盒后，不难发现，网格中心点在包围盒外时，肯定是物面外部的点。该算法的计算量很小，可以帮助快速确定包围盒外部的网格点的类型，但是包围盒内部的网格点类型仍然需要通用的判断方法。很多学者通过简单而且高效的射线相交方法进行上述工作。通常情况下，在要判断的目标点选定任意方向的射线之后，就可以通过计数射线与封闭的物面相交的点数，来判断网格点相对于物面的位置，即相交数目为奇数时，点在内部，偶数时则在外部。然而在使用射线相交方法时，可能存在射线恰好经过外形拐点的情况，导致判断的结果出现错误，如图4所示。图中，和代表目标点，和分别代表经过目标点的射线，代表几何外形，∂代表几何边界，1和2即为经过拐点的射线。

图4 基于射线相交方法判断点在多边形内外Fig.4 Illustration of point inside or outside polygon using ray-casting method

针对上述问题，提出了一种新的鲁棒的判断算法，与射线相交方法相配合，可以准确识别射线经过外形拐点的不同情形。这种方法是通过判断这些线段或面是在射线的同侧还是异侧，若是前者的话，在射线与物面相交点计数时需要在拐点处计数增加1，若是后者的话，则正常计数，本文将这种算法称为奇异性判断算法。

首先以二维情况为例，通过图5和图6说明。在图5中，射线以待判断的目标点为起始点，经过离散线段之间的拐点，两条以为端点的线段分别为和。当满足：

(3)

图5 射线经过拐点示意图：A和B在射线同侧Fig.5 Illustration of ray passing inflection point: A and B on same side of ray

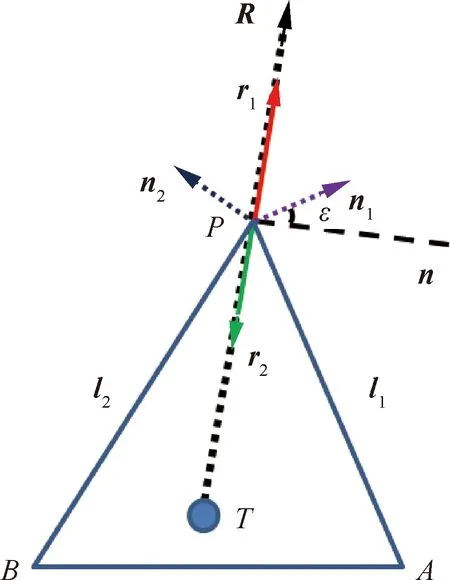
图6 射线经过拐点示意图：A和B在射线异侧Fig.6 Illustration of ray passing inflection point: A and B on different sides of ray

和均在射线的同一侧。其中为以为起点，方向与相同的矢量，则为与之方向相反的矢量。如图5所示。射线与线段对应的向量以及射线的反向矢量与线段对应的向量的夹角分别为和，显然，两条线段分别对应的外法向为和。若=0°或=0°，则射线与其中一条线段重合一定的长度，本文采用重新选择射线方向的处理方式，避免上述重合情况出现。

在图6中，拐点处的线段和在射线的不同侧。这种情形应满足的公式为

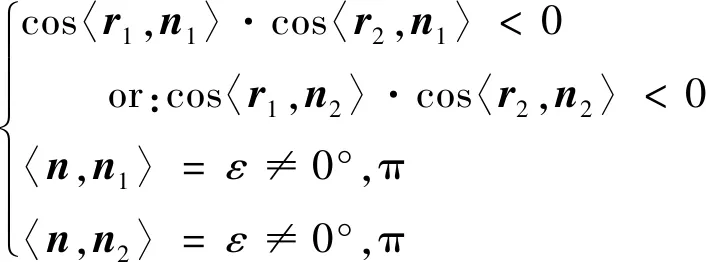
(4)

若〈,〉或〈,〉=0°,π,则同样的,射线与其中一条线段重合一定的长度,需要通过重新选择射线方向的方式进一步判断和处理。

在三维外形的情形下，可以通过选取特定切割平面的方式，通过平面与离散三角形的相交线，转换成二维情况进行计算。

在图7中，射线起点为，经过位于3个离散面上的拐点。此时选取不经过点的任意一条边上任意一点(除了端点)，本文选取的是点，将其与射线上的任意一点(除了起点)以及起点组成切割平面，该平面会切割这些离散三角形得到切割线和。在该切割平面内，就可以按照前面二维的方式来判断射线与离散面之间的位置关系。

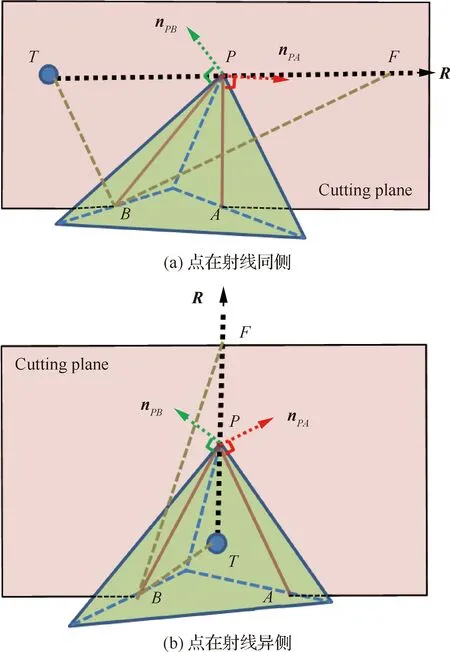
图7 通过切割面将三维问题转化为二维Fig.7 Conversion of 3D problem to 2D by cutting plane passing ray

4.1.2 物面网格快速查找方法

在采用射线相交方法进行判断时，需要计算多个点乘和叉乘，当空间网格和物面网格量比较大时，整体计算量还是很大的。实际上网格类型的判断占据了整个网格生成过程的大部分时间。虽然前面采用几何包围盒进行了过滤，可以缩短一定的判断时间，但十分有限，有必要发展高效的网格类型判断方法。为此，一些学者采用ADT(Alternating Digital Tree)数据结构来存储物面网格，以缩小可能相交的物面单元的检测范围，从而提高射线相交判断的效率。

设空间网格数目为，物面离散单元(线段或三角形)数目为，对于三维构型，是(10)～(10)，而一般是(10)～(10)。在不采用任何优化算法的情况下，即射线相交判断时是逐个物面单元进行计算，此时的时间复杂度为(·)。在采用ADT结构后，可以将相交计算的时间复杂度降低到(·lg)。然而传统的ADT所构建的二叉树的平衡性往往受物面单元的分布密度影响，导致查询效率不稳定。为此，采用其改进版本—KDT结构，其更容易构造平衡优质的二叉树。

KDT是一种多维的二叉树结构，树中的每个节点都是一个-维节点，且每一层都和某个维度相关。其在构造时，需要将当前层的相关点进行排序，然后取中值点，接着确定经过该点与相关维度垂直的平面，以剖分空间搜索区域。由于是以每次排序后得到的中值点作为剖分位置，而不是ADT中的在区域等分点进行划分，因此可以保证多层叉树的平衡性。

下面以一些物面网格点为例，比较两种数据结构的操作复杂度。如图8所示，这些点在数组中存储为：/* A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q */。如果遍历操作的话，需要1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17=153次。

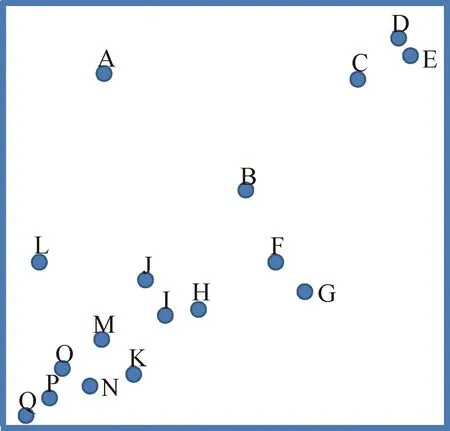
图8 随机排布的网格点Fig.8 Randomly distributed grids

对于ADT叉树结构而言，如图9所示，遍历操作需要1+2+2+3+3+3+4+4+4+4+5+5+5+6+6+7+8=72次。

图9 ADT结构示意图Fig.9 Illustration of ADT

而对于KDT叉树结构而言，如图10所示，遍历操作需要1+2+2+3+3+3+3+4+4+4+4+4+4+4+4+5+5=59次，相对ADT构建了更为平衡的叉树结构，操作的复杂度明显降低。

图10 KDT结构示意图Fig.10 Illustration of KDT

对于物面离散三角形网格构建KD树的主要流程如下：

建立三角形物面网格的空间包围盒，包围盒与坐标轴方向一致，对应着三角形的最大分布空间，可以表示为(,)，其中：

(5)

为三角形网格单元的序号;为空间维度。

构建叉树节点与空间域的对应关系。取三角形的中心点c(=1,2,…,)排序后的中值点作为剖分面经过的点，比较各轴向方向上中心点坐标的方差，最大者对应的方向为剖面的法向，由上面信息即可以确定区域的划分面。

节点的左、右节点对应的空间区域分别记作(,)、(,)，具体为

图11 定义三角面元的坐标范围Fig.11 Definition of coordinate limits for triangular elements

(6)

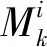
(7)

从根节点开始，通过循环划分，可以将二叉树节点与划分的空间区域逐一对应。

按照步骤2中的对应关系，将物面包围盒逐个插入节点。

(8)

则插入父亲节点的左侧，成为左子节点。如果满足：

(9)

则插入父亲节点的右侧，成为右子节点。

完成上述工作之后，进行射线相交判断时就可以利用构建的KD树，快速查找相交的物面网格，主要步骤如下：

将射线与根节点对应的包围盒进行相交判断，满足相交条件则进行步骤2，否则确定目标点为几何外部的点。

基于KD树进行筛选，逐层缩小检索范围，直至到叶子结点那一层。

判断射线与相交的叶子节点对应的包围盒内的三角形相交情况。

4.2 网格与物面相交判断方法

前面的工作是基于射线相交方法对网格中心点的类型(内部点或外部点)进行判断，这不足以开展网格自适应加密，还需要确定空间网格是否与物面相交。

最原始的方法是对各个网格顶点分别判断网格点的类型，如果同时在内部(或者外部)，则与物面不相交，否则与物面相交。上述方法虽然简单，但是计算量较大。一些学者通过ADT或KD方法直接确定网格与物面的相交情况，可以极大提高网格单元相交判断的效率。其思路是将笛卡尔网格对应的空间区域作为目标区域，在叉树中快速检索与之相交的物面三角形包围盒，进而判断笛卡尔网格与包围盒内的三角形相交与否。这与前面基于KD树的射线相交的快速判断类似。

对于网格与三角形的相交判断，可以归为两类：

1) 三角形整个包含于笛卡尔网格内，这种情况的判断只需比较三角形的包围盒与笛卡尔网格的空间关系，计算量很小，可以很快获得。用(LC, RC)表示笛卡尔网格对应的空间域，当满足以下关系：

LC≤,LC≤

=1,2,…,

(10)

三角形在笛卡尔网格内部,其中为待判断的笛卡尔网格总数。

2) 三角形与笛卡尔网格面相交，如图12所示，可以分解成线段与笛卡尔网格面的相交判断。

图12 笛卡尔网格与三角面元相交示意图Fig.12 Illustration of intersection of Cartesian grids and triangles

4.3 染色算法辅助网格类型判断

在确定笛卡尔网格与物面相交与否后，需要判断非相交网格单元是在物面内部还是外部。若按照4.1节中的方式，则通过射线相交方法对网格中心点位置进行判断，进而获得网格是在内部还是外部的信息。对于封闭的几何外形，可以通过染色算法进一步提高与物面不相交的网格单元类型判断的效率。这种算法是通过查询目标网格的相邻单元(非物面相交单元)的类型，直接给予其相同的网格类型，看起来就像被邻居单元 “染色”了，故称为染色算法。在本文采用的FTT数据结构下，染色算法具有很好的适用性，因为邻居单元查找很便捷。这相对于传统的射线相交方法，计算量会大大减少。

如图13所示，在使用染色方法时，首先要确定染色源，可以取入口边界的第1个网格单元，其必然为物体外部网格，然后与其相邻的单元只要不与物面相交，则同样为外部网格。这种判断方式是面向与物面不相交的网格单元，可以在很快的时间内确定这些单元是在物面内部还是外部，见表1。

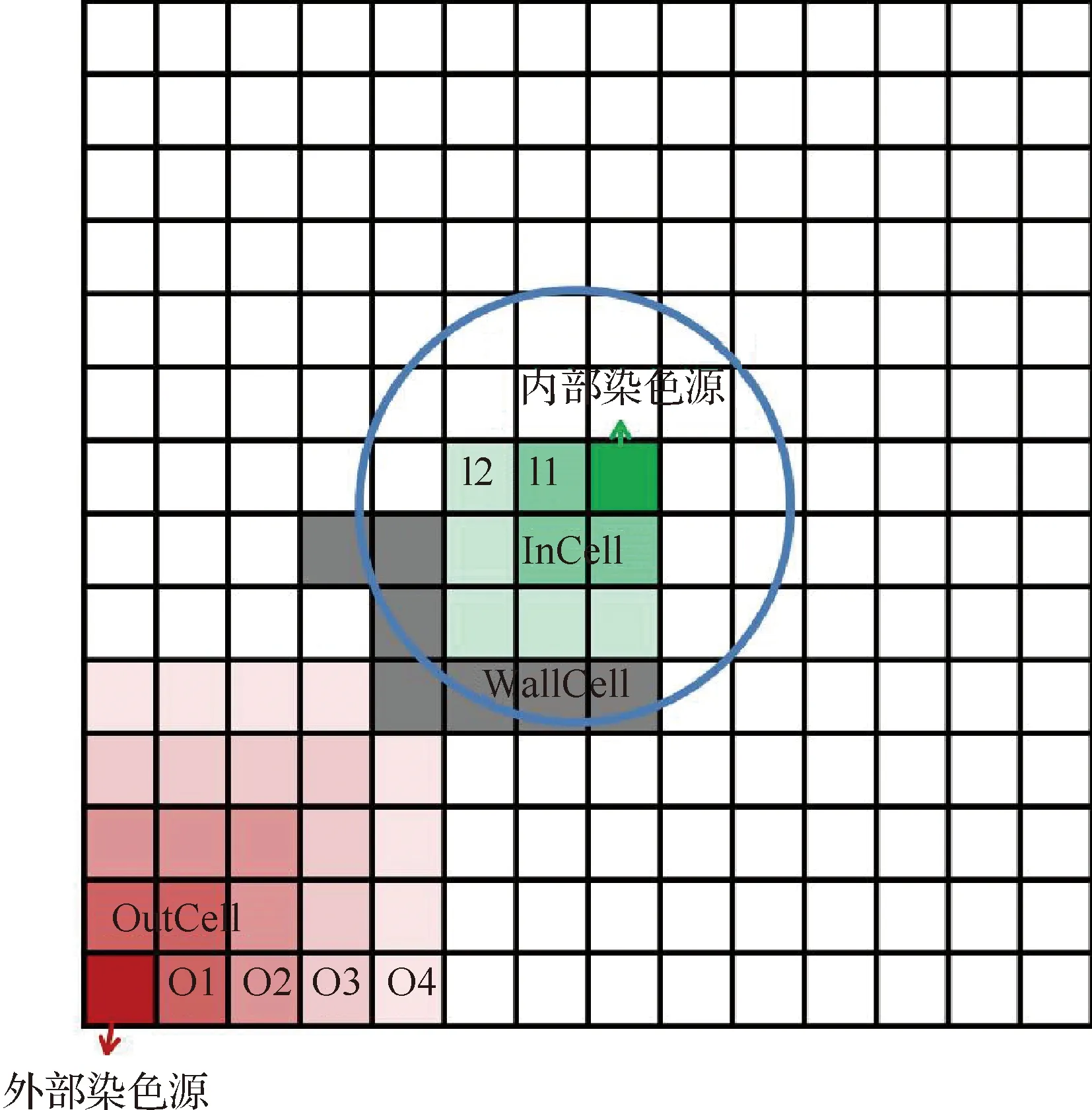
图13 染色算法Fig.13 Painting algorithm

表1 染色算法与传统方法确定网格单元类型对比Table 1 Performance of painting algorithm vs traditional means for determining cell types

5 几何自适应加密

很多学者都探索和建立了可靠的笛卡尔网格几何自适应加密方法。其基本思路是：

1) 将物面相交笛卡尔网格和过渡层网格初步加密特定的次数，具体次数需要根据初始网格和几何外形的尺寸确定。

2) 将物面曲率变化较大的位置进一步加密，主要是通过比较与目标网格相交的相邻物面网格单元法向矢量变化角度，当大于一定阈值时即进行加密。

本文采用上述方式开展几何自适应加密。在加密过程中，需要注意的是，有些区域的网格可能并不合理或质量不高，影响网格对应叉树结构的平衡性以及流场计算的精度和稳定性。例如，在加密一定次数后，相邻网格单元在数据结构中的层次之差大于1，如图14所示。

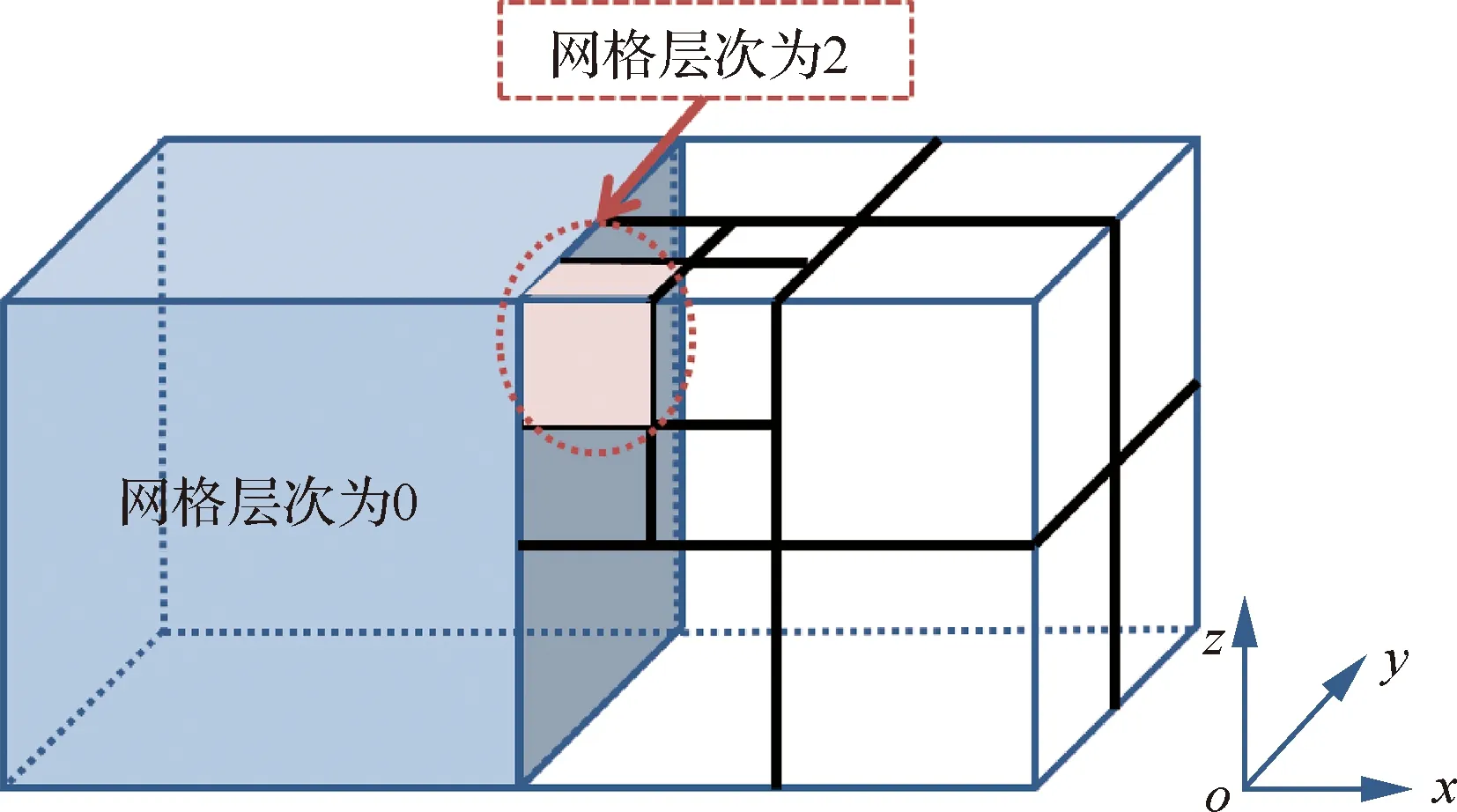
图14 相邻单元层次差大于1Fig.14 Level difference between adjacent cells larger than 1

针对上述情况，在网格加密过程中需要建立一个检测算法，识别上述情形，并对质量差的网格进行加密。本文通过查询目标单元在各个方向上的邻居单元，比较各个邻居单元与目标单元的层次差，当大于1时即对该邻居单元加密，直至层次差等于1。

6 流场解自适应

在完成几何自适应之后，就得到了初始计算网格，但其分辨率对于流动结构的精细捕捉还是不足的，需要基于流场解进行自适应加密，使网格的分布更合理、更有利于刻画流动特征结构。

本文对流动的数值求解基于NND格式对Navier-Stokes方程进行空间离散，时间推进则采用Runge-Kutta方法。为了保证对激波、剪切层、旋涡等多种流动结构的捕捉能力，采用一种综合判据——速度的散度和旋度相结合方式。该判据既可以通过速度的散度捕捉激波，又可以基于速度的旋度捕捉涡旋和剪切层等特征，相对于单一判据具有明显的优势。该判据可表述为

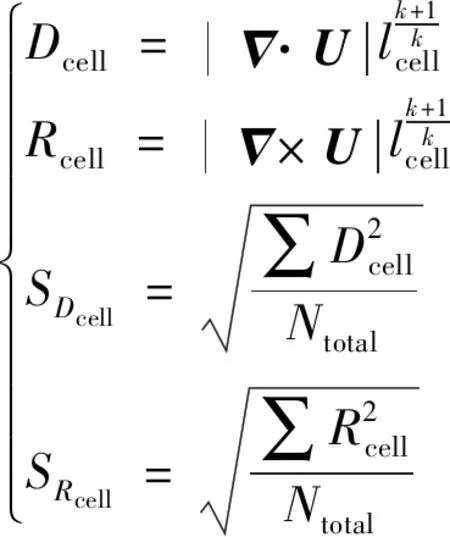
(11)

(12)

式中：、、、为经验系数，在不同的流动问题中并不相同。由于各类流动问题主导特征不同，上述各量在决定网格加密或粗化时起到的作用不同，因而系数设置并不统一。后续研究工作中，将对笛卡尔网格流场自适应判据系数的自动化配置进行研究，进一步提高笛卡尔网格方法的自动化水平。

7 结果和讨论

7.1 圆球算例

表2显示了在CPU为intel core i7-8700，3.2 GHz 台式机上的圆球算例测试结果，网格如图15所示。采用相同的初始网格，固定的几何加密次数为7次，物面网格数目是变化的。虽然物面网格数目不同，但每个单元的CPU时间很接近。这得益于对几何三角形面元构建的KD树结构，使得物面网格密度对于每个单元平均的计算耗时影响不大。

表2 圆球算例网格单元生成类型对比Table 2 Mesh generation after refinement around sphere surface with variable facets

图15 几何自适应网格Fig.15 Geometric adaptive refinement mesh

对本文流场自适应技术进行测试，自适应网格和云图如图16所示。其中来流马赫数=1.5，球半径为=0.5。网格几何自适应加密次数AMR=5，流场自适应加密次数为4。经过几何自适应后笛卡尔网格数目为196 186，经过流场解自适应后网格数目为567 324。

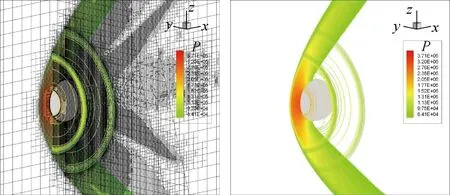
图16 流场自适应网格和云图Fig.16 Adaptive mesh and contour of flow features

激波距离球体驻点的距离计算公式为

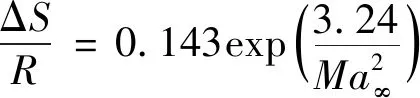
(13)

在来流马赫数为1.5时，上述理论计算值Δ=0302，基于本文方法得到的计算值为 Δ=0310，与理论值相差2.65%，具有较高的吻合度，证明本文数值方法可以对激波位置进行较好的预测。

在平面上，激波形状公式为

=

(14)

是钝体最高点曲率半径，其通过与来流马赫数的关系确定：

(15)

通过式(13)～式(15)可以确定激波形状曲线，如图17所示，与本文数值模拟云图结果对比可以看出，本文结果和理论值能够较好的吻合，对激波位置能够较好的捕捉，证明了本文流场自适应方法和数值格式的可靠性。注意到，本文结果相对理论值仍有细微的偏离，主要是因为流场自适应过程中，细化网格的流场值需要通过粗网格的值插值得到，粗网格分辨率不足和插值计算都会带来一定的误差。

图17 激波位置对比Fig.17 Comparison of shock wave positions

7.2 复杂构型算例

对三维复杂构型的算例进行测试和评估，如图18～图20所示。表3为网格生成算例,物面网格数目从翼身组合体构型的43 128到导弹构型的51 094。表3的第2列和第3列分别为物面三角形数目和加密后的笛卡尔网格数目，第3和第4列分别为在串行时总的CPU时间和每个单元在生成过程中花费的CPU时间。

表3 网格生成复杂构型算例Table 3 Mesh generation tests of complex configurations

图18 导弹构型自适应网格Fig.18 Adaptive mesh of missile

图19 机翼-副翼构型自适应网格Fig.19 Adaptive mesh of wing-aileron configuration

图20 翼身组合体构型自适应网格Fig.20 Adaptive mesh of wing-body configuration

综合各个算例的数据可以看出，本文构建的三维自适应笛卡尔网格生成技术效率很高，这主要归功于以下几个方面：第一，采用的FFT数据结构使得邻居查询遍历层数少，更快捷；第二，通过构建的物面网格单元的KD树结构，使得确定网格单元的位置所需要查找的物面网格的范围极大地缩小；第三，染色算法可以帮助快速确定与物面未相交的单元是在物面内部还是外部。值得注意的是，射线相交和网格与物面相交占据了主要的网格生成CPU时间。KDT结构的应用，可以将潜在的与射线或网格相交的面单元缩小到一个很小的数目。采用该方式，可以查询的复杂度是(·lg)而不是(·)。因此，每个单元生成需要的平均CPU时间受物面网格分辨率和空间网格数目的影响不大。

8 结 论

本文发展了一个面向三维构型的自适应笛卡尔网格生成技术，具备通用性和高效性。为了提高网格生成的效率，采用了几个有效的方法。首先，使用FTT数据结构作为笛卡尔网格数据结构，而不是传统的八叉树数据结构，使得邻居查询更快捷，同时内存利用率更高。对于物面网格的组织方式则是采用平衡性相对传统ADT更好的KDT，尽可能的缩小物面单元查询检索的范围，提高确定网格或射线与物面相交与否的计算效率。网格点在物面内外的确定主要是采用射线相交方法，同时结合染色方法帮助快速确定与物面不相交的单元在物面内部或外部。为了保证射线相交方法的鲁棒性，本文构建了识别经过拐点的射线的判断算法，帮助准确的相交计数。此外，对于基于速度散度和旋度点的三维综合判据进行了发展，经算例测试，显示了较高的可靠性。

通过几个三维的几何构型测试了本文方法，并且得到了鲁棒高效的结果。在接下来工作中，可以通过在一些步骤引入基于GPU的并行加速进程，进一步提高计算效率，缩短网格生成时间。