随机派系网络模型统计性质研究

周志毅，杨翔宇，李子健，丁益民

(湖北大学物理与电子科学学院， 湖北 武汉 430062)

0 引言

近年来，复杂网络的相关研究得到了迅速的发展，其研究涉及数学、物理、生物、计算机、社会科学等诸多领域[1-5].在复杂网络的研究中，一般采用的是将系统中的独立元素抽象为节点，元素之间的相互关系抽象为连边，同构元素之间的关系构成一个可以用数学语言进行表达的复杂网络模型,基于这种思路，人们提出了ER随机网络(Erdos-Renyi random network)模型[1]、WS小世界网络(Watts-Strogtz small world network)模型[2]和SF无标度网络(Scale free network)模型[3].大量的实证研究表明，许多复杂网络同时具有高的聚类系数和短的平均路径长度，呈现小世界特征[2,4]；网络的度分布既有满足指数分布的均匀网络，也有满足幂律分布的非均匀网络，呈现多种度分布特征[3-5]；许多复杂网络还具有模块化的结构以及社团结构特征[6-7].这些网络特征难以用上述3种经典的网络模型解释，为此我们需要改变网络的构建方式，建立更具有普适性的网络模型.

复杂网络社团结构的研究已成复杂网络的一个新的研究热点[8].匈牙利学者Palla等[9-10]提出派系渗流(Clique percolation)的概念，并指出自然界和人类社会中的许多复杂网络都可描述为具有重叠连接的社团结构.美国学者Clauset等[11]在Nature上发表论文，指出层次结构可能是建构复杂网络最重要的组织原则之一,进一步揭示了复杂网络具有层次结构和社团结构的本质特征.日本学者Takemoto等[12]基于派系的概念提出Evolving Networks by Merging Cliques的网络模型.最近，颜嘉麒等[13]将复杂网络中的社团思想运用到新兴的科研领域中，如区块链、智能合约和比特币.

关于网络中的社团结构目前还没有被广泛认可的唯一的定义[14]，不同学者对网络的社团结构提出了不同的定义.Lu Z等[15]提出开发了一种基于群体(即本地完整子网络)的新颖的社团检测方法，Sinha A等[16]提出将通过子图边界的通量度量与子图节点之间的连通性联系起来进行社团网络的的划分.目前对网络中的社团结构进行划分较为常用的是基于相对连接频数的定义:网络中的顶点可以分成组，组内连接稠密而组间连接稀疏.但是这一定义中提到的“稠密”和“稀疏”都没有明确的判断标准.

图1为同一网络社团的2种分割方式,社团分割方式(图1(a))和派系分割方式(图1(b)).不同于社团分割方式，派系分割方式指的是n个完全相互连接的节点构成一个n-派系(n)，将一个复杂网络视为不同大小的派系相互连接构成的网络.

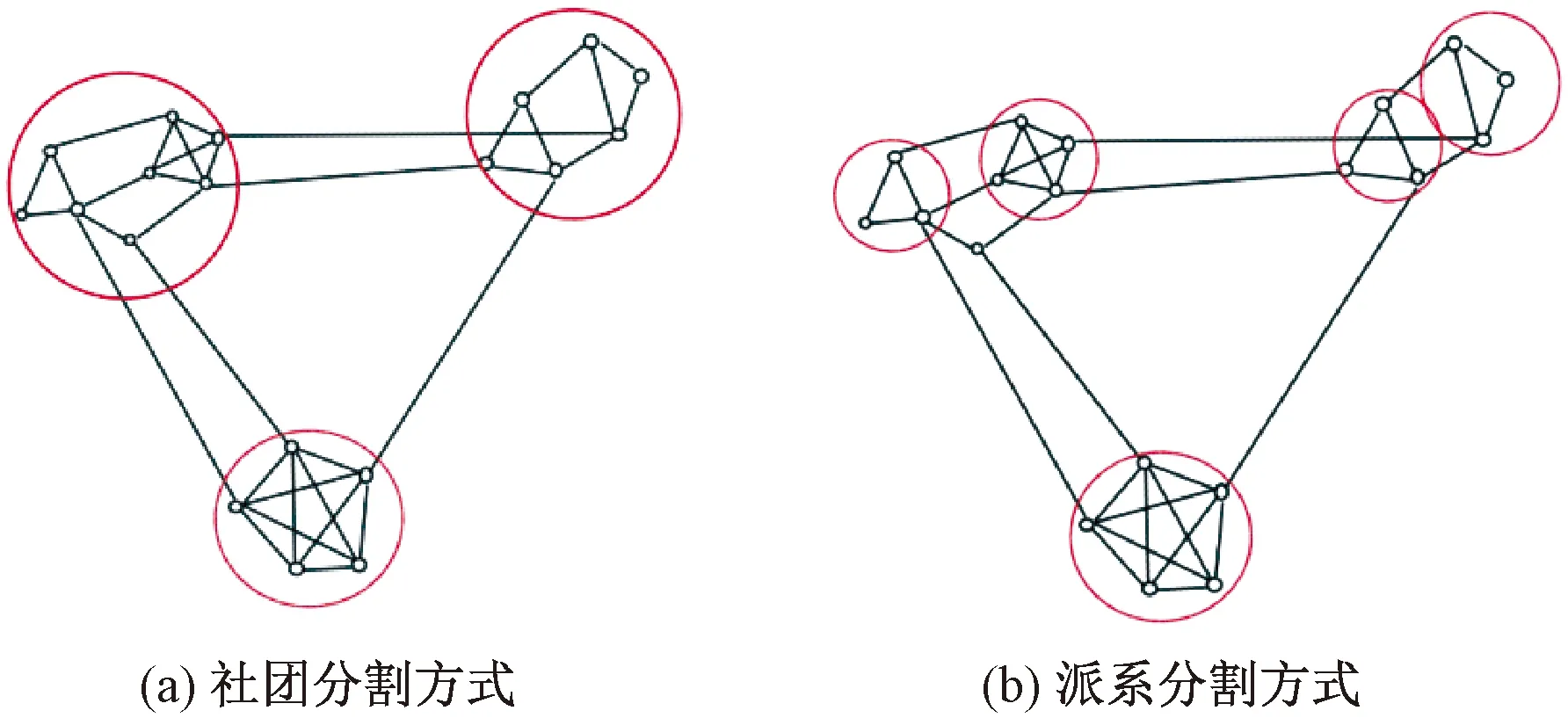
图1 同一网络社团的2种分割方式

Dimitrova等[17]在75个社团网络进行分析时发现，n=3的派系图在网络中占有很大比重，并且这些模块之间互相存在强相关性.Milo R等[18]在研究社团网络相关性质时发现在社团网络中存在元素间具有强关联性的模体，即派系模体，并提出了基于派系网络模体的高阶连通性模式(high-order connectivity patterns)进行社团网络分割的方法.

多位学者对派系网络及其性质从不同的角度进行了研究，Agrawal Smita[19]提出了一种新的基于K-medoids框架的聚类算法SAG-Cluster，用于在节点对断开的情况下使用考虑属性重要性的协同相似性度量来检测社区.国内学者孙豹和王波[20-21]基于派系网络的空间性质对城市公共交通网络进行了研究，并基于派系网络的网络性质提出了基于ArcGIS的公交网络优化系统.我们曾对派系网络进行了一系列的研究，构建了基于派系的社团网络模型，对我国四大城市的地铁网络的网络特征进行了分析[22]，提出了随机派系网络和随机派系生长网络模型，研究了其网络特性[23]、传输能力[24]及渗流相变行为[25].

本研究我们用matlab建模的方法对文献[23]中提出的随机派系网络模型作进一步研究，首先将随机派系网络按自然生长方式提出模型，然后对该模型的度分布、平均路径长度以及聚类系数等网络参量进行数值计算与解析分析，对随机派系网络的网络特性进行较深入的研究.

1 基本定义

1.1 度与度分布度是描述节点在网络中连边数量的物理量[26]，节点i的度ki定义为与此节点连接的边的数目,网络中所有节点i的度ki的平均值称为网络平均度,定义为〈k〉.网络中节点的度分布的分布函数P(k)表示一个任意选择的节点的度恰好为k的概率.

1.2 平均路径长度平均路径长度是表征复杂网络小世界特性的物理量[26]，网络中2个节点i和j之间的距离dij定义为连接这2个节点的最短路径上的边数.网络中任意2个节点之间距离的最大值称为网络的直径D,网络平均路径长度〈l〉为所有2个节点(节点对)之间距离的平均值，即:

(1)

1.3 聚类系数聚类系数是表征复杂网络的小集团结构特征的物理量[26]，假设网络中的一个节点i有ki条边，每条边均和其他节点相连,这ki个节点被称为节点i的邻居,而聚类系数ci指其所有邻居节点之间实际存在的边数ei和总的可能的边数目ki(ki-1)/2之比,即:

(2)

2 网络模型

参考 ER 随机网络的构建方法：

1)给定网络节点总数N；

2)在每一步时间T，任意选2个节点连边；

3)当总边数达到n时停止演化.

考虑到现实网络多数通过自然生长方式构建，我们提出自然生长的随机派系网络模型的构建方式，图2是n=3、N=10时不同演化阶段T时刻下的随机派系网络演化图，其构建方法：

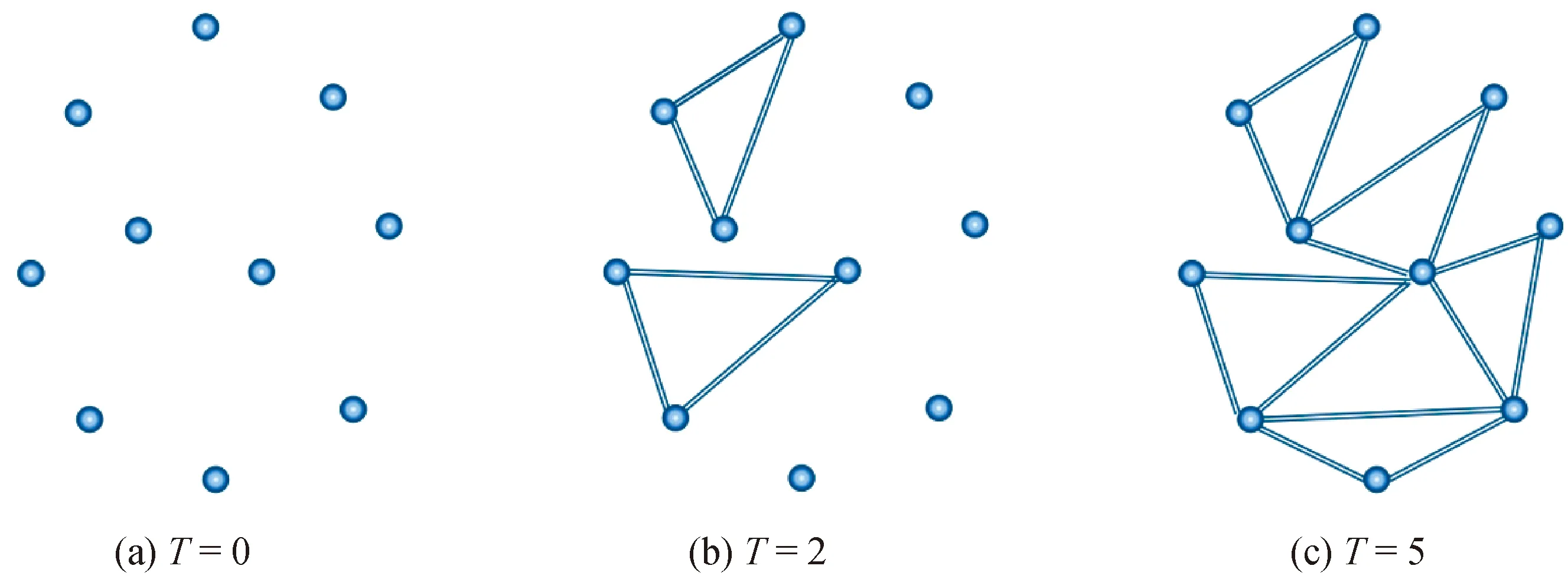
图2 不同演化阶段T时刻下的随机派系网络演化图

1)确立网络规模，给定N个未连边的节点和L条总连边数；

2)在每一步时间T，随机选择n(n≤N)个不同的节点相互连接构成一个n-派系；

3)继续重复选择n个不同的节点直到网络构成一个联通图.

此方法可以视为ER随机网络的变式，在随机派系网络构建时用派系模体替代连边，当n=2时的随机派系网络即退化为ER随机网络.因此随机派系网络可看成是ER随机网络的推广.

3 随机派系网络的性质

我们首先利用matlab软件对自然生长的随机派系网络模型进行仿真模拟，分别研究派系大小n为2～10的纯派系网络的度分布、聚类系数和平均路径长度.对于自然生长的随机派系网络，设当自然生长为联通图时，网络总连边数为L，为了有效地减小数值计算的误差，每个参数在计算时均取50次重复计算的平均值.

3.1 度分布度分布是描述网络特性的重要物理量，由于本派系网络采用的是随机联边选择方式，其网络的度分布与ER网络相同，遵循泊松分布[26]：

(3)

我们用Monte Carlo方法模拟当N=5 000时，随机派系网络的度分布情况.当n=3时，随机派系网络的度分布如图3(a)所示，不难发现该网络具有度分布分级的结构，并且每层分级结构服从泊松分布.当n> 3时，随机派系网络的度分布出现更为复杂多层的分级结构(如图3(b)所示).度分布分层现象在实现世界的复杂网络并不少见，我国学者何大韧研究组[27]曾报道对我国南京、杭州、北京和上海的公交线路网络的实证研究结果，不难发现四大城市的公交线路网络均显示出度分布分层现象，这是由于公交线路网络在P空间中可看成为由不同大小派系按随机方式演化的网络[22]，度分布分层现象是派系结构网络的宏观体现.

图3 随机派系网络的度分布图

对于随机派系网络的度分布分级现象，我们解释如下：一个随机选点构建的网络，每个点被选择到的次数分布也满足泊松分布.对于一个n=3的随机派系网络，不考虑重复连边(同一条或多条边同时出现在一个以上的派系中)的情况下，随机派系网络的度分布只有偶数度分布；考虑重复连边的情况下，n=3的随机派系网络单一节点的度将增加1，且这一分布也满足泊松分布.对于更为复杂的情况，如n=5的随机派系网络，不考虑重复连边的情况下，由于形成一次派系将使节点的度增加4，故网络的度分布将是4的倍数.考虑到重复连边情况，将使网络中单一节点的度增加1～4，且这些分布也满足泊松分布，故对于一个n=5的随机派系网络的度分布将出现4层分层的泊松分布.

3.2 平均路径长度基于随机派系网络模型的自然生长的计算机模拟，当网络中N个节点(N=5 000)形成联通图时，随机派系网络的平均路径长度〈l〉与派系大小n的关系如图4所示，可见平均路径长度〈l〉随着派系大小n的增大而减小，表明派系大小n越大，网络的总连边数就越大，网络的平均路径长度就越小.

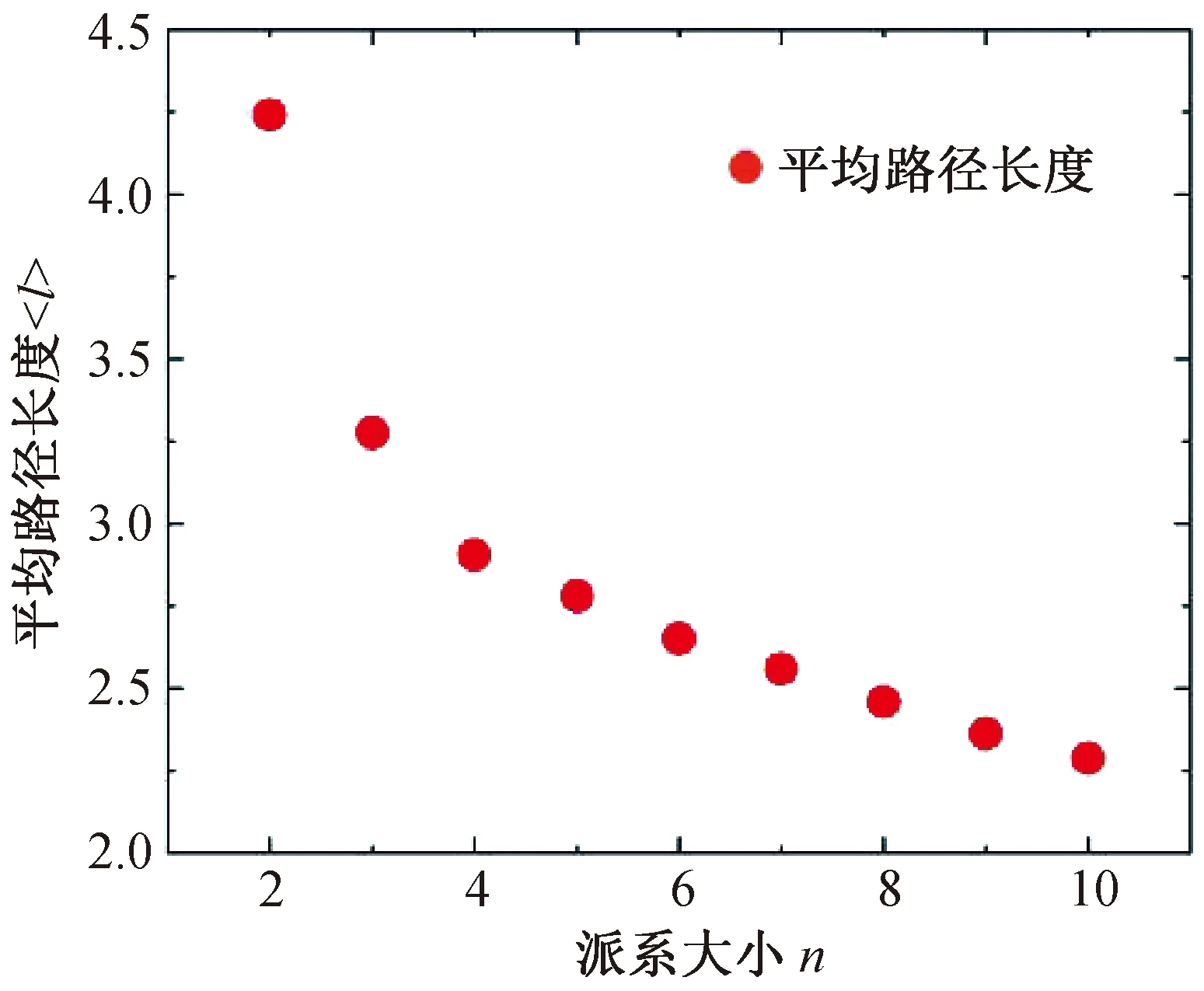
图4 随机网络的平均路径长度〈l〉与派系大小n的关系

对此我们作以下近似分析：任选一个节点，与它相距为1的节点即邻点有〈k〉个，每一个邻点又有相同多的邻点，其邻点中有n- 2个点是这一邻点的邻点，所以与它相距2的节点有〈k〉(〈k〉-n+2)个.在不考虑更复杂的邻点重复的情况下，可近似认为与它相距为l(l>1)的所有节点的邻点数均为〈k〉-n+2个，与它相距〈l〉的节点有〈k〉(〈k〉-n+2)〈l〉个，由于度分布是泊松分布，可以近似认为所有节点对之间的距离均是〈l〉,即〈k〉(〈k〉-n+2)〈l-1〉=N,所以得到：

(4)

由(4)式不难发现，平均路径长度〈l〉随着网络的平均度〈k〉的增大而减小，与计算机模拟结果相符.

3.3 网络的聚类系数我们还计算了当N=5 000个节点形成联通图时，n为2～10的随机派系网络的聚类系数C与派系大小n的关系，如图5所示，红色三角点为聚类系数的平均值，可以看到相对于ER随机网络(n=2)，n> 3的派系网络聚类系数有明显的增加.并且网络的聚类系数C随着派系大小n的增大而增大.

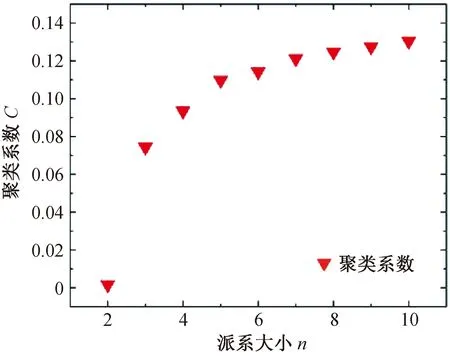
图5 派系网络的聚类系数C与派系大小n的关系

(5)

随机派系网络的网络聚类系数为各节点聚类系数的平均值，即

(6)

由(5)式可知，聚类系数C随派系大小n的增大而增大.

3.4 网络大小L与派系大小n的关系我们还研究随机派系网络的网络大小L与派系大小n的关系，网络大小L与派系大小n的对应关系如图6所示，红色圆点为网络大小的数据，绿色虚线为拟合线.可以发现，网络大小L与派系大小n呈线性关系，可拟合为一次函数关系，并且网络大小L随着派系大小n的增大而增大.

图6 网络大小L与派系大小n的关系

对此我们做以下近似分析：求解N个节点随机选点，使每个点均被选到一次所需选点次数的统计平均值是概率论中赠券收集问题的变式.赠券收集问题为：假设有N种赠券，每次取1张赠券，每种赠券的的获取几率相同，而赠券亦无限供应，则需要多少次才能集齐全部赠券.赠券收集问题的严格解为：

z1=NlnN+γN+1/2

(7)

(8)

数据拟合结果为：

L=44 969.74n-42 730.82

其结果与我们理论推演的结果相符.

综上所述，随机派系网络不同于ER随机网络，它是一个具有高的聚类系数和短的平均路径长度的网络，可以较好地描述现实世界网络的高聚类和小世界的性质.我们知道WS小世界网络模型是最经典的小世界网络模型，随机派系网络模型为小世界网络模型的构建提供一种新的方案.

4 结束语

本文中从派系模体出发，参考ER网络的构建与分析方法，按自然生长方式构建出随机派系网络模型，并与ER网络模型进行对比研究.研究发现随机派系网络的度分布服从多重泊松分布，且派系大小n越大，分层越多；随机派系网络相比于ER随机网络具有更高的聚类系数，且派系大小n越大，聚类系数C越大；随机派系网络相比于ER随机网络具有更短的平均路径长度，且派系大小n越大，平均路径长度〈l〉越短.即随机派系网络模型是一个具有高的聚类系数和短的平均路径长度的网络模型，可以较好地描述现实中的复杂网络的高聚类小世界的性质.网络的度分布、平均路径长度和聚类系数等参数是一个复杂网络的宏观参数，n-派系则是一个网络的具体构成部分.类比与热力学与统计物理学的相关思路，我们希望通过提出更多的网络具体构成部分(微观参量)与合适的网络参数(宏观参量)对复杂网络的性质进行分析，为分析复杂网络的性质提供一个新的思路.

致谢感谢湖北大学物理与电子科学学院周斌教授对论文数值计算给予技术指导和计算设备的支持，感谢中国科学院物理研究所叶方富研究员在解析计算方面的指导，感谢湖北大学物理与电子科学学院本科生曹宇晗等同学在计算机模拟方面的支持.