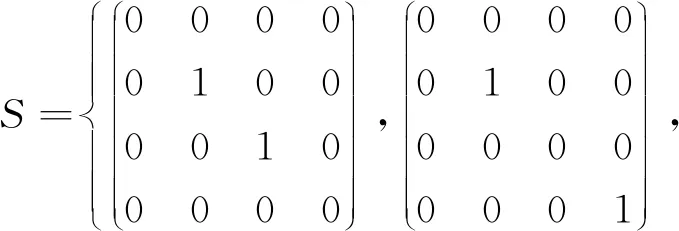
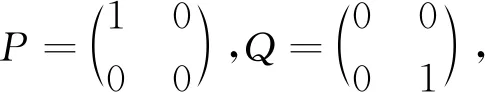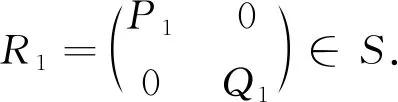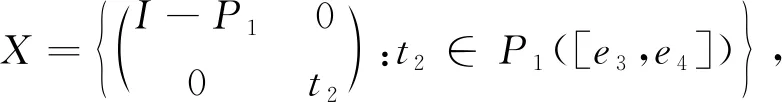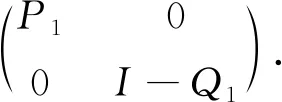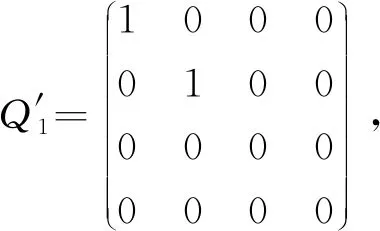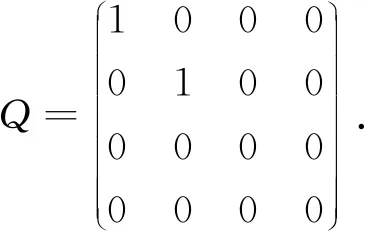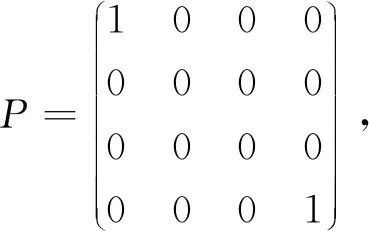秩2投影集的几何结构

向 彰

(重庆师范大学 数学科学学院, 重庆 401331)

0 引言

1931年Wigner[1]首次提及Wigner定理.Wigner定理有非双射版本与双射两个版本.非双射版本说明Grassmann空间上保持不同射线之间夹角的变换由线性等距或者共轭线性等距导出.另一方面,在Hilbert空间的维数不小于3时, Uhlhorn观察到：若Grassmann空间上的变换是保持正交性的双射,则非双射版本中的等距算子就是一个酉算子或者反酉算子.双射版本的Wigner定理叙述如下：

设H是Hilbert空间,P1(H)为秩1投影形成的集合.如果φ是P1(H)上的等距满射，则存在酉算子或者反酉算子U使得

φ(P)=UPU*,∀P∈P1(H).

Wigner定理提出之后,它的推广引起了学者们的极大兴趣.Botelho等[2]首次刻画了Pn(H)上的算子范数等距满射，并指出：当dimH≥4n时,Pn(H)上的算子范数等距满射φ由酉算子或反酉算子导出.为了去掉维数的影响,Geher等[3]采用不同于文献[2]的方法证明了Pn(H)上的算子范数等距满射φ是由酉算子或者反酉算子导出.对于任意P,Q∈Pn(H),定义了集合

M(P,Q)={R∈Pn(H):‖P-R‖=

文献[3]首先证明了P,Q正交当且仅当M(P,Q)是紧流形.然后,因为φ是等距满射, 所以φ(M(P,Q))=M(φ(P),φ(Q)),从而证明了φ保持投影的正交性.最后,运用文献[4]的结果得出φ由酉算子或者反酉算子导出.文献[3]的证明思路启发我们考虑P,Q正交时,与P,Q距离为1的秩n投影形成的集合.然而,由于P,Q之外的元相互关系很复杂,这种集合的刻画较困难.于是本文考虑了Pn(H)中任意两个元距离为1的子集，将这种集合定义为等距集，不被任何等距集包含的等距集称为极大等距集.

本文首先给出一些概念和引理.然后研究了dimH=4时,P2(H)中极大等距集的三种形式.

1 预备知识

设H是复Hilbert空间,本文所有命题和定理中H均为4维复希尔伯特空间.Pk(H)是H到H的所有秩k投影形成的集合.当M是H闭子空间时,P(M)表示值域为M的投影,Pk(M)表示M中秩k的投影.当N是H的子集时,[N]表示包含集合N的最小闭子空间.

定义1设H是Hilbert空间,dimH=n<∞,k∈Z+,k

引理1若{P,Q,R}是等距集,则P∧R,Q∧R∈P1(H).

证明由于‖R-P‖=‖R-Q‖=1,所以存在

0≠ξ1∈ImR∩KerP,

0≠ξ2∈ImR∩KerQ，

因为P,Q正交,所以P∧R,Q∧R正交,因此P∧R+Q∧R是投影.又因为R∈P2(H),所以R=P∧R+Q∧R.

2 主要结果

定理1P,Q∈P2(H)并且P,Q正交.S是包含P,Q的极大等距集,那么S的形式是

证明由P,Q正交,所以在正交分解H=ImP⊕ImQ下,

t1∈P1([e1,e2]),t2∈P1([e3,e4]).

情况1X∩S有两个元时.不妨设这两个元为

情况2Y∩S基数为2时,类似情况1讨论.

不论是情况1还是情况2,可以验证X∩S,Y∩S中均有两个元.

定理2Q1,Q2∈P2(H),‖Q1-Q2‖=1并且dim(ImQ1∩ImQ2)=1,则包含Q1,Q2的极大等距集S的基数为6.

证明因为Q1,Q2∈P2(H),‖Q1-Q2‖=1,dim(ImQ1∩ImQ2)=1,所以总可以选定H的一组规范正交基e1,e2,e3,e4，使得Q1,Q2的矩阵表示如下：

设{Q1,Q2,P}是等距集.由于‖P-Q1‖=1,ImP中有非零元0≠η1=λ1e1+λ4e4∈[e1,e4].类似地,因为‖P-Q2‖=1,于是ImP中有非零元η1=μ1e1+μ3e3∈[e1,e3].

(i)η1,η2线性无关时.显然此时η1,η2形成ImP的一组基,又由于η1,η2∈[e1,e2,e3],因此有P∈P2([e1,e3,e4]).

(ii)η1,η2线性相关时.如果λ4≠0,μ3=0,由于η2的非零性,我们就有μ1≠0,于是就有η2=μ1e1,这与η1,η2线性相关矛盾.类似地,λ4=0,μ3≠0是不可能的.而λ4≠0,μ3≠0时,η1,η2必然线性无关.因此λ4=0,μ3=0.进而

其中R=P1([e2,e3,e4]).

由于S-{Q1,Q2}中任意元T与Q1,Q2形成等距集，因此S-{Q1,Q2}中的元是(i)或(ii)形式.为了方便我们将S-{Q1,Q2}中(i)形式的元形成集合记为X，(ii)形式的元形成集合记为Y.因为X⊆P2([e1,e3,e4]),所以X中至多有三个元.由于[e2,e3,e4]至多含有三个相互正交的秩1投影，所以Y中元的个数不会超过3.

情况1X中有三个元时.

其中P1,P2,P3是P2([e1,e3,e4])中两两正交的三个秩2投影.

情况2Y中有三个元时.

设Q1,Q2,Q3∈Y.不妨设Q1,Q2,Q3的形式如下：

Q1=P([e1])+R1,Q2=P([e1])+R2,

Q3=P([e1])+R3,

其中R1,R2,R3是P1([e2,e3,e4])中相互正交的三个秩1投影.若S中有X中元P′1，由于{Q1,Q2,Q3,P′1}也是等距集，e1∈ImQi(i=1,2,3),所以存在非零ξi∈ImP′i∩[e3,e4]使得ξi⊥ImQi.

(i)ξ1,ξ2,ξ3张成一维线性空间时,有ξ1∈[e3,e4]使得ξ1⊥[e2,e3,e4](矛盾).

(ii)ξ1,ξ2,ξ3张成二维线性空间时,由于ξ1,ξ2,ξ3∈[e3,e4],我们就有P′1=P([e3,e4]).因此在情况2下,

其中Q1,Q2,Q3∈Y.

情况3X中有两个元P1,P2.

若Q∈Y,则有{P1,P2,Q}也是等距集.因此存在非零ξi∈ImQ∩KerPi,于是

P([e1,e3,e4])ξi∈P([e1,e3,e4])(KerPi)(i=1,2).

(i)P([e1,e3,e4])ξ1(i=1,2)中至少有一个为0.在这种情况下ξ1,ξ2中至少有一个与e2线性相关,故我们得到e2∈ImQ.因此有

(ii)P([e1,e3,e4])ξ1≠0(i=1,2)，因为0≠ξ1∈P([e1,e3,e4])(KerPi)(i=1,2),因此有ξ1,ξ2线性无关，进而Q=[ξ1,ξ2].

情况4X中有一个元时.

显然S的基数至多为6.

注定理2给出两个元的交是1维的极大交换集S的结构，我们很自然会问：是否存在一个极大等距集S，使得S中任意两个元的交是0维的且S的基数是6？上面的定理只得出S的基数不大于6,S的基数是否为6还需进一步研究.在接下来的部分我们用R=L(ξ1,ξ1)表示秩2投影P2([ξ1,ξ2]),并且不再区分闭子空间与投影.

定理3设H是4维的Hilbert空间,S⊆P2(H)，S是等距集.若S中任意两个元的交是1维的,则S的基数不会超过6.

证明不妨假设P,Q∈S,因为P,Q∈P2(H),‖P-Q‖=1,dim(ImP∩ImQ)=0,因此总可以选定一组规范正交基使得P,Q的矩阵表示如下：

其中0<λ≤1.

如果λ=1，则有P⊥Q.由前面引理1，我们可以知道‖R-P‖=‖R-Q‖=1，必有dim(R∩Q)=1，因此S={P,Q}.于是我们只需考虑0<λ≤1的情形.

不妨设KerQ=[e1,e3+te4].由于‖R-P‖=1,‖R-Q‖=1,于是存在0≠ξ1∈ImR∩kerP,因此有ξ1形如λ2e2+λ3e3.存在ξ2∈ImR∩kerQ，因此有ξ2形如λ1e1+α(e3+te4).

下面证明[ζ1,ζ2]=ImR.假设λ2=0,则有e3∈ImR.于是有

λ1e1+α(e3+e4)-αe3=λ1e1+αe4∈ImR，

这与dim(ImR∩ImP)=0矛盾.因此λ2≠0，ξ1,ξ2线性无关,并且ξ1,ξ2张成ImR.由于λ2≠0我们不妨将ξ1写成e2+λe3.

接下来再说明λ1≠0.假设λ1=0,我们不妨将ξ2写成e3+te4.设k1,k2∈C满足

e2+λe3+k1(e3+te4)=e2+k2(te3-e4).

(1)

对(1)式中各项的系数，我们得到一个关于k1,k2的二元一次方程组：

容易验证线性方程系数矩阵行列式非零，于是k1,k2有非零解,这与ImR∩ImQ=0矛盾.因此我们得到投影R形式为R1=L(e2+λe3,e1+μ(e3+te4)),为了方便起见我们记

α={L(e2+λe3,e1+μ(e3+te4)):λ,μ,t∈C}.

下面先证α中任意两个元交为0. 设

R1,R2∈α，R1=L(e2+λ1e3,e1+μ1(e3+e4)),

R2=L(e2+λ2e3,e1+μ2(e3+e4)).

若ImR1∩ImR2≠0，则存在非零的复数c1,c2,m1,m2,使得

c1e2+c2(e3+te4)=m1e2+m2(e3+te4).

(2)

将上式两边同时对e1,e2作内积，我们可以得出c1=m1,c2=m2(矛盾).

最后再证S∩α至多有4个元.设R1,R2如上.若‖R2-R1‖=1则∃η∈ImR2,使得η⊥R1.因此存在k1,k2∈C，使得

η=k1(e2+λ2e3)+k2(e1+μ1(e3+te4))=λ1e2-e3+**.

(3)

因此就有

(4)

整理后得出

(1+λ2λ1)+μ1μ2+μ1μ2t2(1+λ2λ1)=0.

(5)

于是得到了‖R2-R1‖=1的必要条件是(1+λ2λ1)+μ1μ2+μ1μ2t2(1+λ2λ1)=0.我们观察到整个推导过程都是可逆的，因此这个条件是一个充要条件.

R1,R2如上,若{P,Q,R1,R2,R}⊆S,R=L(e2+xe3,e1+y(e3+e4)),则有

由方程(b)我们可以得到

y=(1+t2+t2λ1x)-1μ-1(-1-λ1x)，

(6)

将(6)式带入(c)得到

(μ1-μ2)λ1λ2t2x2+[2(λ2μ1-λ1μ2)+(λ1μ1-λ2μ2)t2]x+(μ1-μ2)(1+t2)=0.

(7)

在R1,R2固定的情形下，即λ1,λ2,μ1,μ2固定.由前面的分析知μ1≠μ2,λ1≠λ2,于是(7)是一个关于x的一元二次方程.由于一元二次方程根的个数不超过2,所以α中至多有4个元.