基于典型任务剖面的装甲车辆驾驶训练评价研究

梁媛媛, 张 晶, 金晓辉, 高若曼

(1.中国人民解放军63966部队,北京100072；2.北京交通大学机 电工程学院,北京100044)

目前，我军装甲车辆驾驶训练缺乏完备的信息化辅助手段，装备训练评价体系不够全面.尤其是开展驾驶训练任务时，对驾驶员驾驶行为分析评价的技术和理论工具不完善，难以实现对驾驶员驾驶细节的准确评判，无法给驾驶员提出全面准确的评价以及针对性指导，不利于高效、高质量地完成训练任务.

驾驶训练评价是一个复杂的过程，不同的评价指标对评价结果有着不同程度的影响，各个评价指标之间也存在着一定干扰，这些影响难以直接量化，从而增加了给出合理的驾驶员驾驶训练结果的难度.比如，有经验的驾驶员驾驶任务完成状态良好，但可能驾驶动作与训练标准有一定差距；又如新手驾驶员驾驶动作与训练标准较接近，但驾驶任务完成情况一般等.文中将综合考虑驾驶员生理与心理状态、驾驶动作、车辆运行状态以及训练数据4个方面，构建驾驶员驾驶训练评价指标体系，建立综合训练评价模型.对驾驶员的驾驶训练表现进行较为全面的评价.

1 评价指标体系构建及指标权重确定

1.1 评价指标确定

驾驶员在完成装甲车驾驶训练任务时，驾驶训练结果不仅与驾驶员的驾驶动作有关，也受到天气环境状况、装甲车运行情况等多方面因素的影响.因此，评价驾驶员的驾驶训练情况时，不仅要关注驾驶员的驾驶动作，也应考虑车辆状态等其他因素.选择合适的评价指标，可提升对驾驶员驾驶训练结果评价的准确性，也可以提高评价效率.

驾驶训练评价的总目标是综合评判驾驶员的驾驶水平.一级指标分为驾驶员生理和心理状态、驾驶员驾驶动作、车辆运行状态和训练数据4个部分，每个一级指标又细分为多个二级评价指标[1].文中构建驾驶训练评价指标体系，如图1所示.

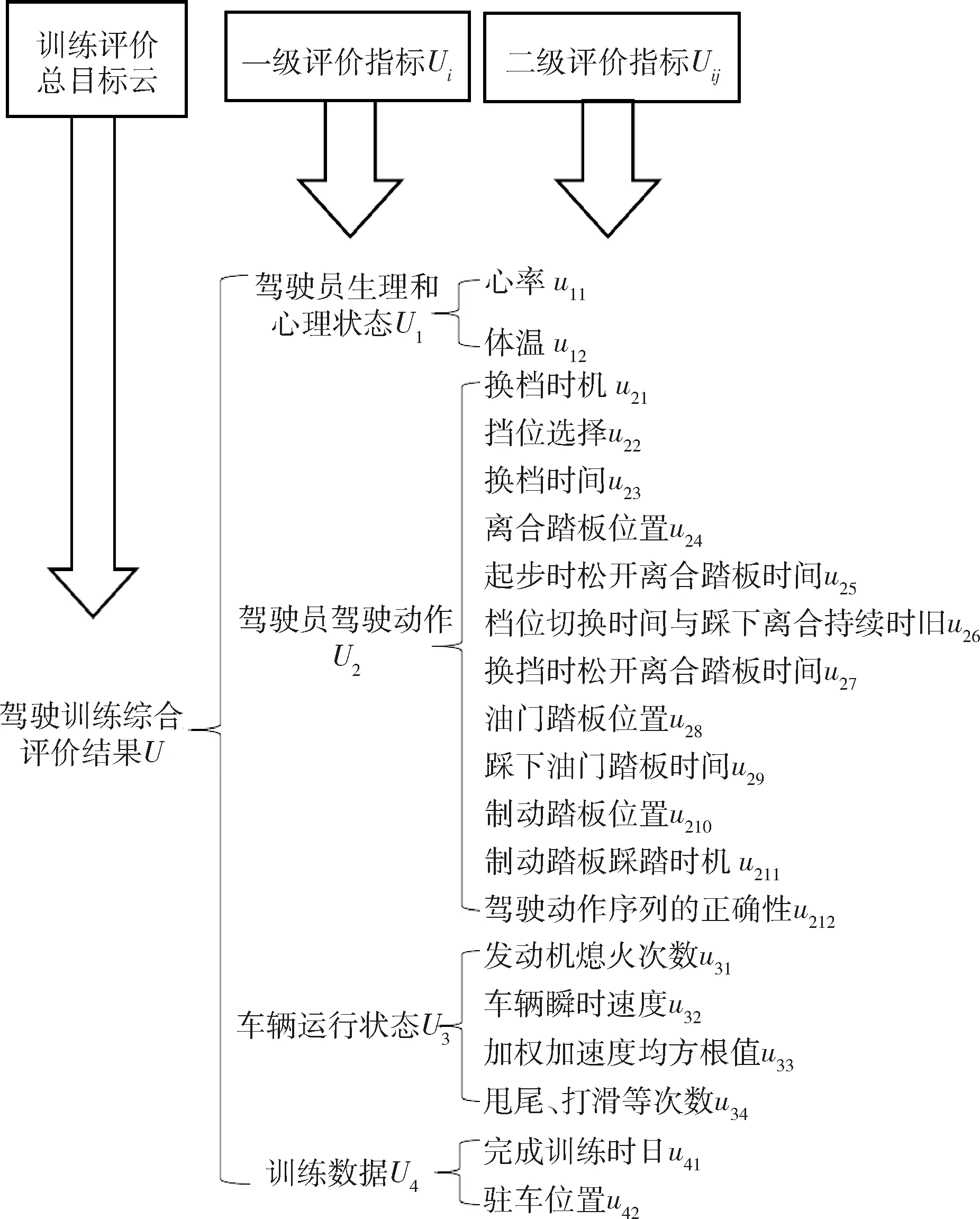
图1 驾驶训练评价指标体系

1.2 基于AHP层次分析法构建判断矩阵

为反映各因素的重要程度，同时保证评价的科学性，通过对比多种权重确定方法，文中选择AHP层次分析法确定不同评价指标的权重.AHP层次分析法是美国运筹学家萨蒂提出的一种系统分析方法[2-6].该方法将定性分析方法与定量分析方法相结合，将复杂问题划分为若干因素，然后将各因素两两比较,最终确定各要素的权重系数.AHP层次分析法解决问题的具体流程见图2.

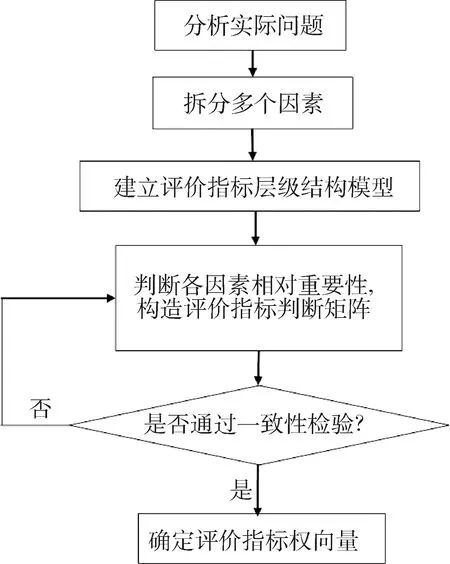
图2 AHP层次分析法确定权重流程

设有n个一级评价指标U1,U2,…,Un，对总目标层U有影响，且对U的影响重要程度不同.每次同时选取两个指标Ui,Uj对比，用aij(>0)表示指标Ui对U和指标Uj对U的影响之比.将所有对比结果用矩阵A表示，其中，aji=1/aij(i,j=1,2,…,n).同理，二级评价指标uij对其所对应的一级评价指标Ui的影响也能用该矩阵表示.构建矩阵过程中，需要进行n(n-1)/2次两两判断.

(1)

人们利用AHP层次分析法研究问题时，提出了不同的标度规则.其中，1-9标度规则使用方便、计算简单，但相邻标度之间绝对差值较大，合理性较低；且评价指标达到5个时，1-9标度规则的判断矩阵一致性关系较差，适用于构建4阶以内的低阶判断矩阵.而0.618标度规则适合于评价指标达到5个的判断矩阵的构建；10/10-18/2标度规则极大改善了1-9标度规则的性能，计算结果更为合理.通过对比不同标度规则的特点，文中采用10/10-18/2标度规则开展研究.10/10-18/2标度规则如表1所示.

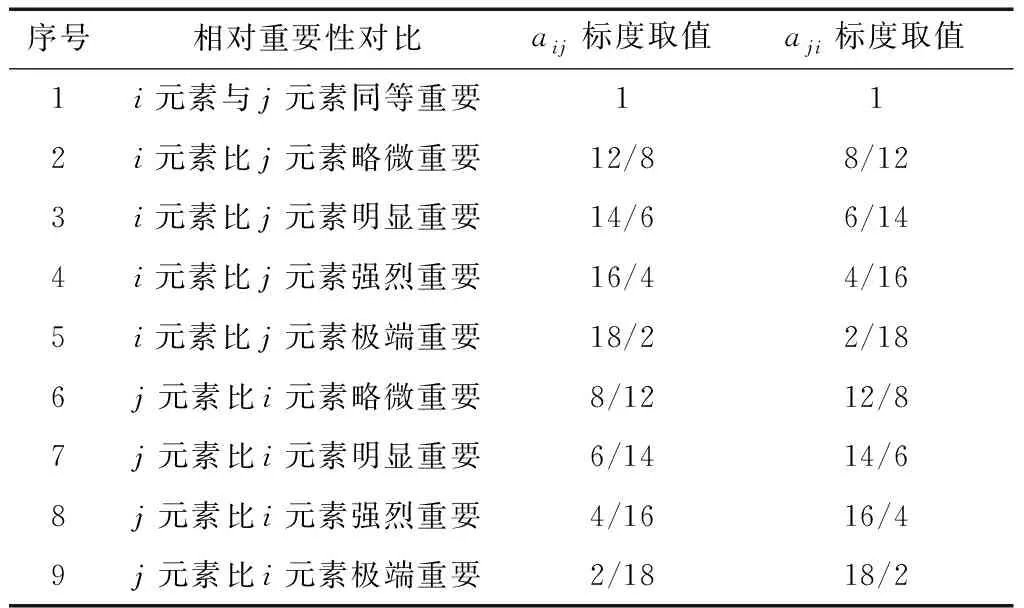
表1 10/10-18/2标度规则表

驾驶训练评价指标的重要性各不相同,为减少主观因素影响，邀请8名专家根据10/10-18/2标度规则各自打分，互不影响，然后，求取均值确定指标重要性，构造判断矩阵.整理得到一级评价指标对总目标层的判断矩阵、各二级评价指标对一级评价指标的判断矩阵，表示如下：

(2)

(3)

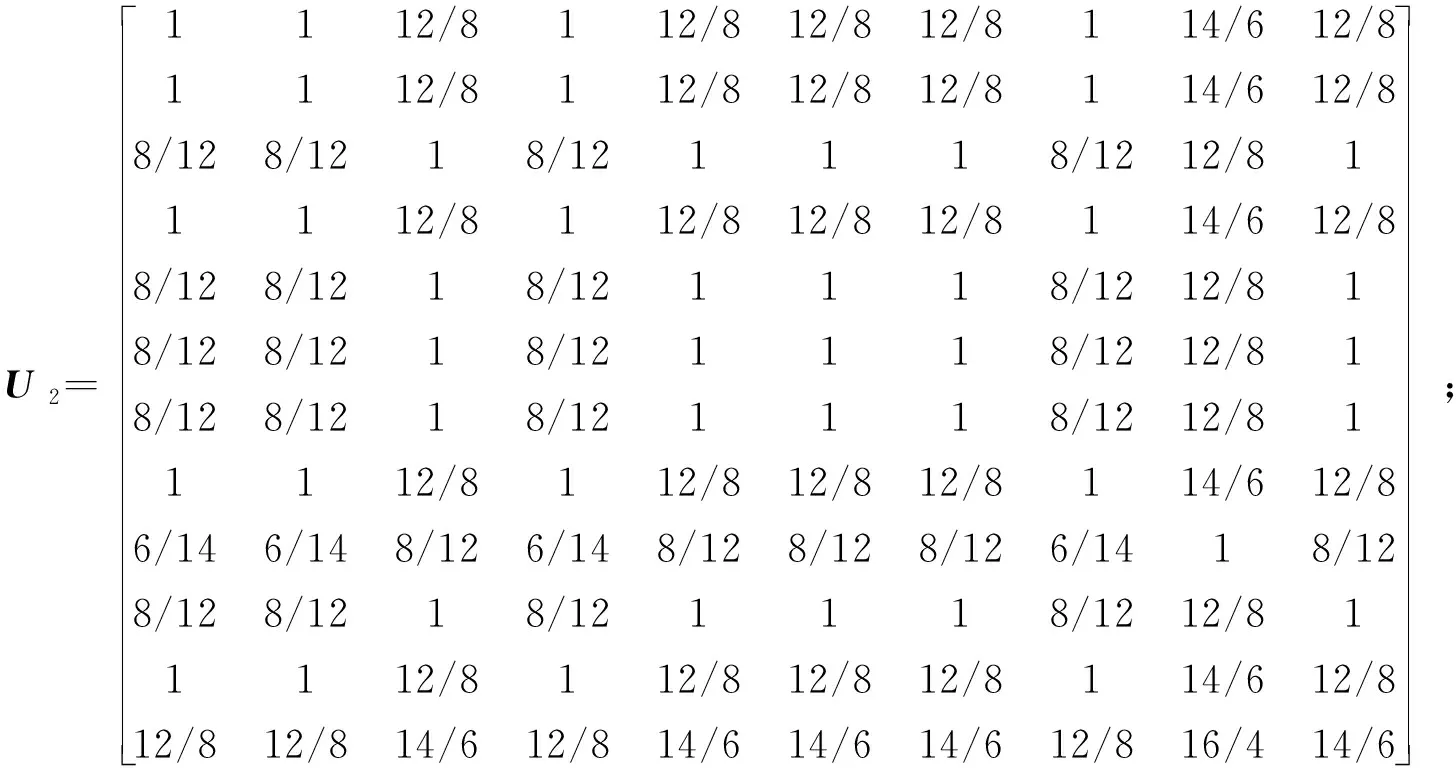
(4)

(5)

(6)

由于专家们对评价指标的认识和判断标准各不相同，所构造的判断矩阵不一定准确，因此,需要对判断矩阵进行一致性检验.首先，计算出各个矩阵的最大特征值λmax，再根据矩阵阶数n用下式计算一致性检验指标CI.

(7)

CI的值越小，则矩阵一致性越好.当CI=0时，认为该矩阵具有完全一致性；当CI≠0时，则需要利用检验系数CR=CI/RI进行进一步检验.当CR﹤0.1时，则认为矩阵一致性很好；否则需要对判断矩阵的值进行重新判断，直到CR<0.1.

其中，RI是平均随机一致性指标，它的值与阶数有关，具体取值如表2所示.对判断矩阵分别计算与分析，得到的一致性检验结果如表3所示.

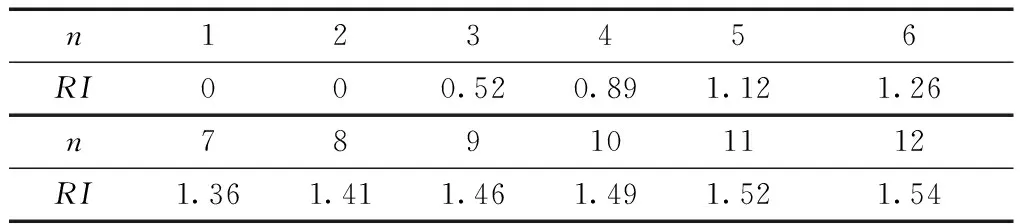
表2 平均随机一致性指标取值

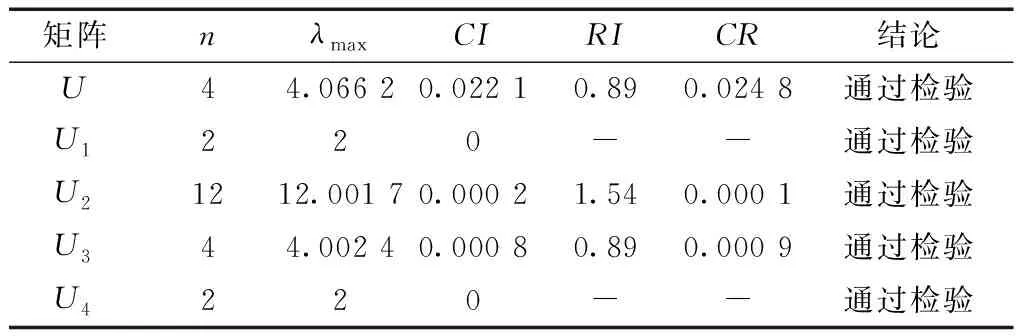
表3 判断矩阵一致性检验结果

由表3结果可以看出，所有判断矩阵均通过了一致性检验，其中，矩阵U1和U4具有完全一致性.

1.3 指标权重确定

基于前文的分析与计算，可以得到评价指标分别占上一级评价指标的权重，从而可以得到二级评价指标占总目标U的权重.根据下列公式计算各个指标的权重

(8)

式中:wij为各个指标所占权重.

通过计算可以得到所有评价指标的权重，如表4所示.

表4 评价指标权重

从表中结果可以看出，一级评价指标中驾驶训练数据U4最为重要，其次重要的是驾驶员驾驶动作U2.二级评价指标中，完成训练的时间u41、驻车位置u42、发动机熄火次数u31对训练评价结果的影响最大.

2 二级指标评价模型建立

基于所建立的评价指标体系，结合现有驾驶训练指导资料及相关文献，针对每项评价指标建立评价模型，为驾驶训练评价软件的开发奠定理论基础[7].文中采用百分制对各项指标进行打分，因此,通过加权计算后的驾驶员训练满分成绩为一百分.驾驶员驾驶训练总的评价结果用V表示，它是各项评价指标对应的评价结果与对应权重系数乘积之和，通过下式计算.

(9)

式中:wij(i=1, 2, …，m;j=1, 2, …,n)为各个指标所占权重；Bij(i=1, 2, …，m;j=1, 2, …,n)为各指标的评价结果.

接下来对各项评价指标建立驾驶训练评价数学模型.

2.1 驾驶员生理与心理状态U1

心率u11：人的正常心率范围在每分钟60～100次.当驾驶员心跳不大于每分钟100次时，说明驾驶员身体状态正常，甚至有身体素质较好者心率会低于每分钟60次；当驾驶员心跳大于每分钟100次时，可能是由于驾驶员精神状态紧张、恐惧等情况引起的，应提醒驾驶员冷静驾驶，并有意训练、提高驾驶员心理素质.心率过高则应扣除适当分数，提醒驾驶员增强身体素质与心理素质的锻炼.设驾驶员训练结束后测量的心率为x11，心率的评价模型如下:

(10)

体温u12：人的正常体温在36-37.3 ℃范围内，在紧张和害怕时,会导致体温升高.设驾驶员训练结束后测量的体温为x12，体温的评价模型如下：

(11)

2.2 驾驶员驾驶动作U2

换挡时机u21：前文研究得到最佳动力性换挡规律，将作为驾驶员换挡时机的评价标准.驾驶员实际换挡过程中，设最佳动力性换挡车速为v(x21)，读取驾驶员驾驶训练数据中换挡时的车速为vi′(x21).考虑到车辆行驶过程中车速的波动，计算时，设定1 km/h为允许的误差范围，在此范围内均可获得满分；当速度差超过1 km/h，但未超过5 km/h时，给出评分计算公式，分阶段评价；当速度差超过5 km/h时，驾驶员实际训练数据与参考值差距过大，评价指标换挡时机的得分为0.假设某次训练中应该进行m次换挡操作，第i次(i=1, 2,…,m)的评价结果用下式计算：

(12)

式中：“[x]”为取整函数，表示不超过实数x的最大整数.假如v' (x21)与v(x21)之差的绝对值为1.6，则[|v′(x21)-v(x21)|]=1，驾驶员该项指标扣10分，即得分为B21(x21)=90.

整个训练中，该项指标的得分为每次换挡评分bi(x21)的均值，则指标u21的评价模型表示如下:

(13)

挡位选择u22：指标u22用于评价驾驶员是否根据路况与行驶需求合理使用挡位，使车辆发挥出最大动力性.设某次驾驶训练任务中，某时刻驾驶员应使用的挡位为gi(x22)，读取驾驶员驾驶训练此时所用的挡位为gi' (x22).有所研究装备的参数知道gi' (x22)和gi(x22)的取值集合为{1, 2, 3, 4, 5}.假设某次训练中应该进行m次换挡操作，第i次(i=1, 2,…,m)的评价结果用下式计算.

(14)

整个训练中,该项指标的得分为每次换挡评分bi(x22)的均值，则指标u22的评价模型表示如下:

(15)

离合踏板位置u24：离合踏板实际所处的位置占踩踏到底时踏板位置的比例.由于离合踏板位置一直在变化，为了能更准确地描述离合踏板实验数据与标准数据的关系，文中选择标准差来评价.设驾驶训练过程中，用于评价参考的离合踏板位置为hi(x24)，驾驶员实际训练过程中的离合踏板位置为hi′(x24)，其中，i表示整个训练任务中共包含i(i=1, 2,…,m)个数据点，hi′(x24)与hi(x24)为相同位移下对应的值.则可以求出离合踏板位置实验值偏离评价标准的程度为

.

(16)

(17)

式中，“[x]”为取整函数，表示不超过实数x的最大整数.假如bi(x24)为15，则[bi(x24)/10]=2，驾驶员该项指标得分为B24(x24)=80.

同理，可以得到油门踏板位置、制动踏板位置、松开离合踏板时间等驾驶动作评价指标的评价模型，在此不再赘述.

2.3 车辆运行状态U3

发动机熄火次数u31：发动机熄火次数能够体现驾驶员驾驶技能的熟练度.有经验的驾驶员能够合理地完成驾驶相关操作，并使车辆保持较稳定的工作状况；而驾驶经验不足的驾驶员容易因操作不熟练或错误操作导致发动机熄火，影响车辆稳定运行状态.用发动机熄火次数指标进行评判时，熄火次数越多，驾驶员驾驶熟练程度越低.设驾驶员训练数据中熄火次数为n′(x31)，n(x31)为非负整数.具体评价模型如下：

.

(18)

车辆瞬时速度u32：对比驾驶员实际驾驶车速与评价参考时，通过对比车辆实际速度与速度评价标准给出评价.行驶过程中的车速并不是平稳升降而是波动变化的，为了能更准确的描述车速的实验数据与评价标准数据的关系，选择标准差来评价.

设驾驶训练过程中，用于评价参考的车速为hi(x32)，驾驶员实际训练的车速为hi′(x32)，其中，i表示整个训练任务中共包含i(i=1, 2,…,m)个数据点，hi′(x32)与hi(x32)为相同位移下对应的值.则可以求出车速的实验值偏离评价标准的程度为

.

(19)

因此，指标u32的评价模型可表示如下：

(20)

2.4 训练数据U4

驻车位置u42：装甲车辆驾驶场景多样，如陡坡路、弹坑、悬崖等恶劣环境或是装备托运等实际需要，都应在指定的区域内及时驻车.因此，定点驻车驾驶能力是驾驶员的一项必备技能.驾驶训练时应注意培养驾驶员对装备制动的感受能力，提升制动的驾驶技能.一般装甲车辆体型较大，为解决具体驻车位置不好界定的问题，文中将驻车点统一规定为测量装备履带最前侧轮心的垂直距离.如图3中的A点所示.

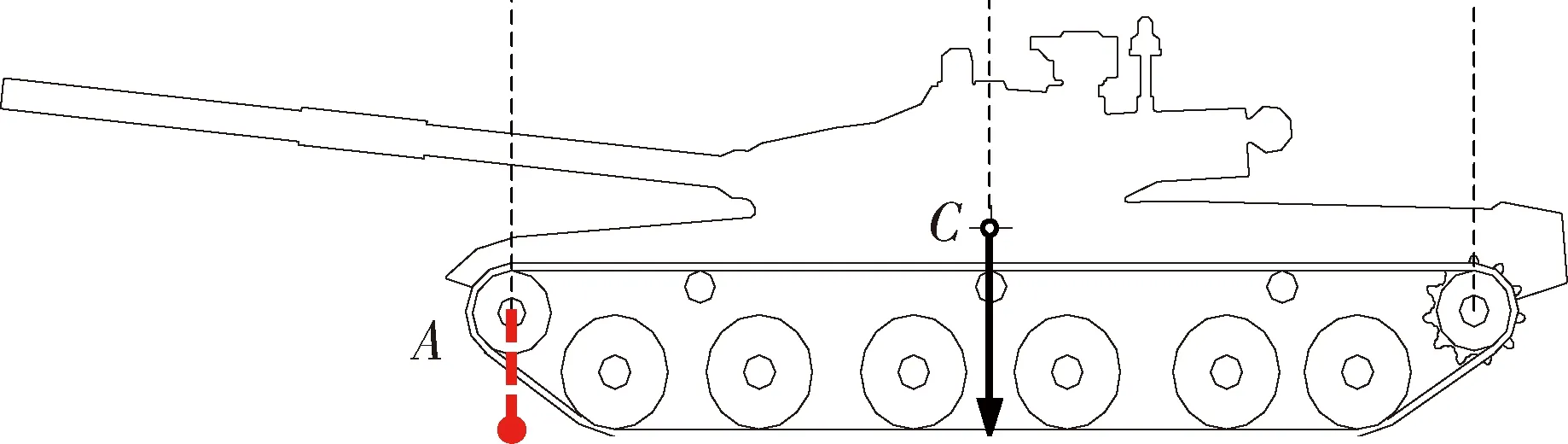
图3 驻车位置测量点示意图

设指定的驾驶训练驻车位置为a(x42)，驾驶员完成驾驶训练后，实际的驻车位置为a′(x42)，测量a(x42)与a′(x42)两点之间的距离用d(x42)=a′(x42) -a(x42)表示，单位为m.其中，d(x42)=a′(x42)-a(x42)大于零时,表示A点没有超过指定驻车位置;d(x42)=a′(x42)-a(x42)小于零时,表示A点超过了指定驻车位置.考虑定点驻车的难度，设定实际驻车位置与指定点之间有1m的误差允许，在此误差范围内均可获得满分.该指标评价模型规则如下:

.

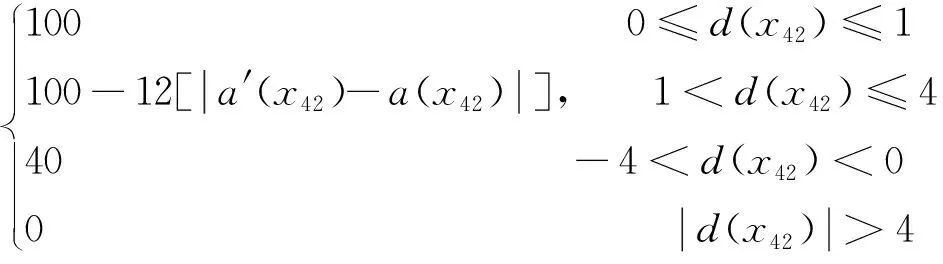
(21)

基于前文所建立的评价数学模型，在MATLAB中建立评价仿真模型.读取驾驶员实际训练数据后，可以分别求得驾驶员的单项指标的评价结果，再由各指标的权重计算出驾驶员综合成绩.

3 驾驶训练评价示例

接下来以4位不同水平驾驶员的驾驶训练数据为例进行评价，通过训练数据与评价标准间的计算关系得到相应成绩，验证评价模型是否合理.驾驶员基本情况如表5所示.其中，装甲车驾驶员的驾驶等级从低到高依次为D、C、B、A，随着驾驶等级的升高，驾驶员的驾驶水平也逐渐提高.

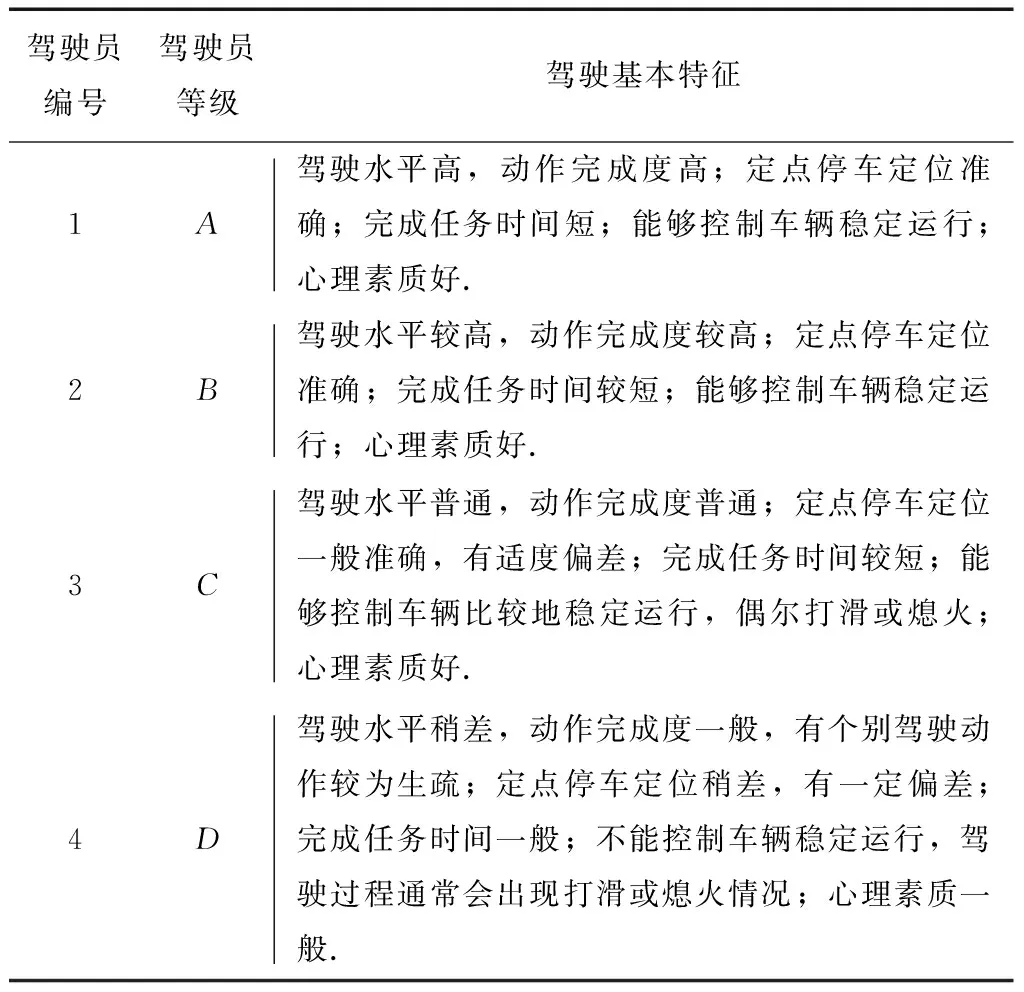
表5 不同驾驶员的基本情况

1号驾驶员的驾驶评价结果如表6所示.

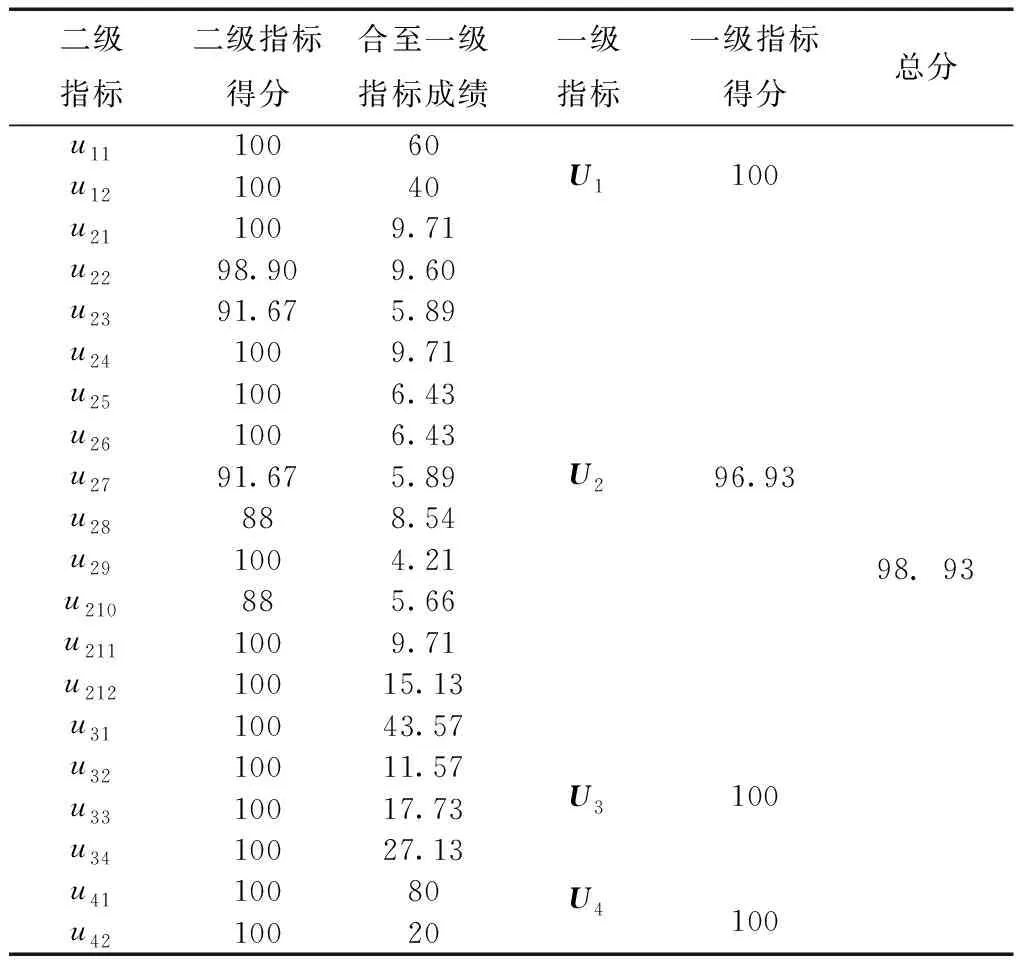
表6 驾驶员1的训练评价结果

从评价结果可以看出，驾驶员1在进行驾驶训练时，能够很好地完成各个驾驶动作，也能很好地控制车辆达到目标车速，说明该驾驶员对车辆的控制能力很强，有很高的驾驶水平.

其余驾驶员的驾驶训练评价结果如表7所示.

表7 其余驾驶员的训练评价结果

通过对比评价成绩和驾驶员等级，可以发现文中所建立的评价模型科学、合理，能够清晰地区分出不同等级的驾驶员，验证了所建立评价模型的科学性与实用性；同时能够知道驾驶员身体状况、驾驶动作、车辆运行状况等方面的具体表现情况.有助于驾驶员合理认识自己的表现，帮助驾驶员有针对性地练习，提升驾驶水平与作战效率，对驾驶员驾驶训练具有重要的指导意义.

4 结 论

基于我国现有的装甲车辆驾驶训练评价方法，文中综合考虑了驾驶员生理与心理状态、驾驶动作、车辆运行状态以及训练数据4个方面，构建了驾驶员驾驶训练评价指标体系，并利用AHP层次分析法确定评价指标的权重系数，在此基础上,建立了综合训练评价模型.经过不同水平驾驶员驾驶训练数据的验证，发现文中建立的驾驶训练综合评价模型能够很好地区分驾驶员驾驶水平，能够对驾驶员的驾驶行为进行较为全面且准确的评价，对驾驶员驾驶训练有一定指导作用.文中建立的评价模型，为军队装甲车辆驾驶训练评价提供方法与技术支撑，具有一定的经济意义和军事意义.