基于MPC和模糊控制的智能汽车路径追踪研究

石振新, 冯剑波, 王衍学

(北京建筑大学，北京 102616)

随着人工智能和汽车工业的发展，智能汽车已成为车辆工程领域的研究前沿，对车辆高度智能化的控制能够解放人们的双手，提高道路通行能力.路径跟踪控制是实现智能行驶的关键环节，通过已知的路径，计算出车辆当前状态下所需要的方向盘转角，使得车辆能够按照预设的路径行驶[1].进行轨迹追踪前，就要规划出合理的跟随路径.文中参考了文献[2]中的五阶多项式的避障路径，满足多种约束条件的同时不会增加模型的复杂性和计算时间.汽车是一个非完整约束系统，其非线性特点使得很多因素无法分析求解，使得在执行汽车轨迹跟踪控制时要考虑多种约束，十分复杂.而MPC算法能够有效地解决这种带约束的问题[3]，在自动驾驶领域应用越来越多.文献[4]中就基于MPC算法通过控制前轮实现了车辆对双移线轨迹的跟踪.此外，在高速转向工况下，由于车辆的侧向加速度很大，稳定性降低，车身会出现震荡摆动，导致轨迹跟踪偏差较大.Peng等[5]通过直接横摆力矩控制来纠正车身姿态，使汽车按照理想的轨迹行驶.鉴于此，文中以横摆角速度及质心侧偏角误差值为双输入，通过模糊控制器输出横摆力矩施加至车轮，以减少高速工况下轨迹的偏差.

综上，文中采用MPC算法跟踪路径，通过模糊控制修正偏差，最后，通过CarSim/Simulink联合仿真验证了本轨迹跟踪控制方案的有效性.

1 汽车动力学建模

文中研究的是车辆高速情况下的轨迹追踪问题，为提高控制器的实时性，减少计算量，将车辆模型进行如下假设：①假设车辆无垂向运动且不受悬架的影响；②忽略空气阻力以及前后轴载荷转移；③假设车辆为前驱且仅为前轮转向.

基于以上假设，车辆三自由度模型等同于单轨模型，如图1所示.

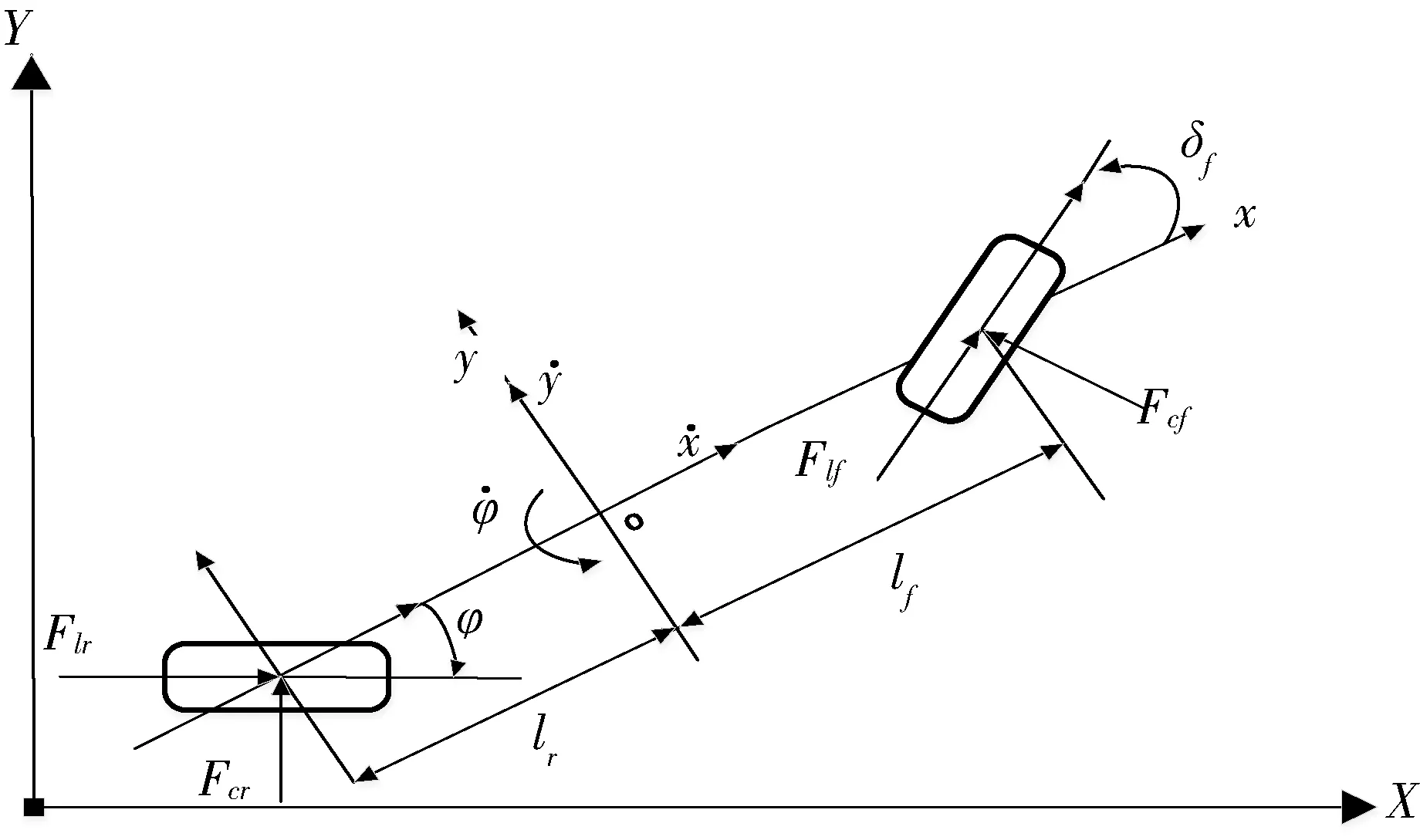
图1 三自由度车辆模型

由上图模型，可得车辆动力学方程为

(1)

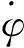
轮胎力可线性表示为

(2)

式中：Ccf、Ccr为前后轮轮胎侧偏刚度；αf、αr为前后轮轮胎侧偏角；Clf、Clr为前后轮胎纵向刚度；sf、sr为前后轮轮胎滑移率.

将(2)代入(1)，可得到简化的非线性车辆动力学模型：

.

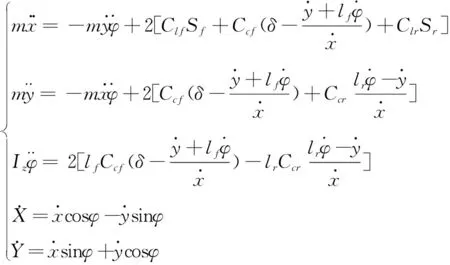
(3)

2 基于MPC的轨迹追踪控制器的设计

基于式(3)所建立的车辆动力学模型是非线性的，为了减少控制器计算量，提高实时性，对模型进行离散化处理，得到线性方程为

.

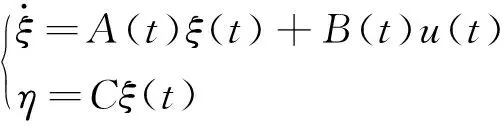
(4)

对雅可比矩阵求解得：

对式(4)进行离散化处理，可得

(5)

式中:Ak=AT+I;Bk=BT;T为采样时间.

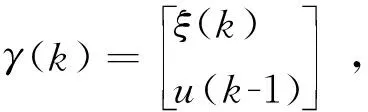
(6)

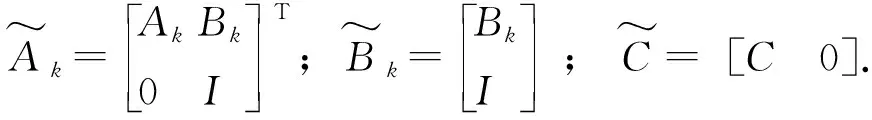
此时，系统的输出量可表示为

Y(t)=ψtγ((t|t)+ΘtΔU(t)，

(7)

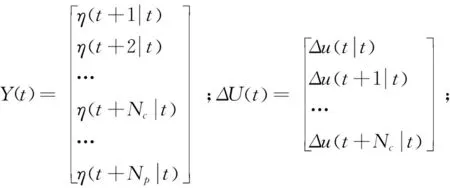
控制器的目标函数要能够保证自车快速且平稳地追踪期望路径，设计如下目标成本函数.

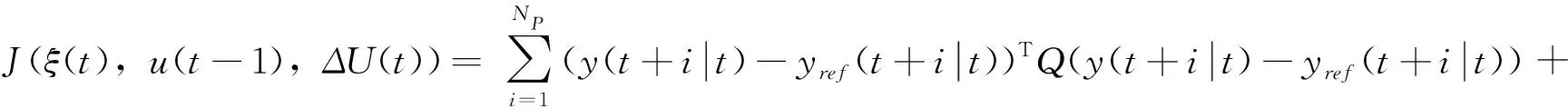
(8)

式中:P,R为权重矩阵;ε为松弛因子.保证目标函数具有可行解.式(8)中前两项反映了系统对于参考路径的跟踪能力，第三项反映了对控制量变化的约束.

为进一步保障车辆行驶的安全性和稳定性，进行以下约束条件设计：

.

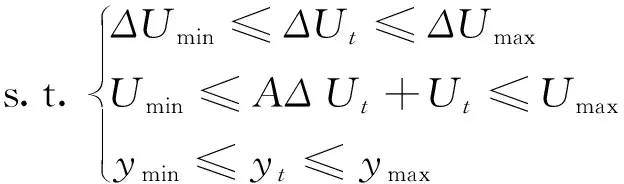
(9)

在每个控制周期完成上述求解后，将控制序列中的第一个元素作用于控制系统，在下一时刻，重复上述操作，以此实现对系统的持续控制.

3 基于模糊控制的偏差修正部分

针对高速工况下跟踪轨迹偏差较大的问题，文中以横摆角速度误差值及质心侧偏角误差值为双输入，通过模糊控制，输出横摆力矩施加至车轮以减少偏差[6].

理想的横摆角速度φref，理想的质心侧偏角βref表达式如下[7].

,

(10)

,

(11)

式中:vx为车辆纵向速度；μ为路面附着系数；k为稳定性因数；L为轴距.

输入量质心侧偏角误差Δβ和横摆角速度误差Δφ均定义为5个语言变量:{NB，NS，ZE，PS，PB}={负大，负小，零，正小，正大}，Δβ和Δφ二者的模糊子集如图2所示.输出量额外的横摆力矩ΔM定义为7个语言变量:{NB，NM，NS，ZE，PS，PM，PB}={负大，负中，负小，零，正小，正中，正大}，ΔM的模糊子集如图3所示.

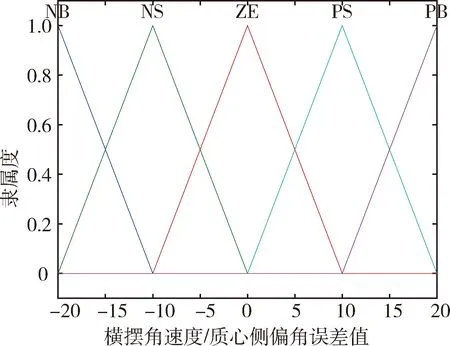
图2 输入量模糊子集

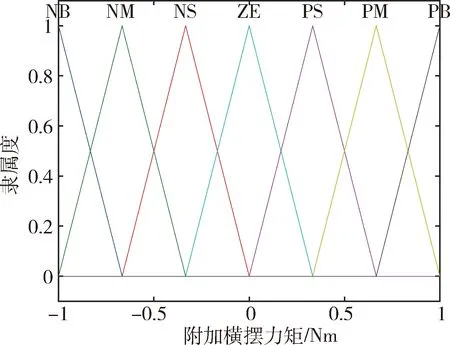
图3 输出量模糊子集

现制定模糊规则，当Δφ<0，Δβ<0时，此时就需要通过反向横摆力矩(ΔM<0)施加至车轮来减小误差，即Δφ、Δβ均为NB，ΔM为PB;若Δφ>0，Δβ>0时,则需要通过正向横摆力矩(ΔM>0)施加至车轮来减小误差，即Δφ、Δβ均为PB，ΔM为NB，所有模糊规则如表1所示.

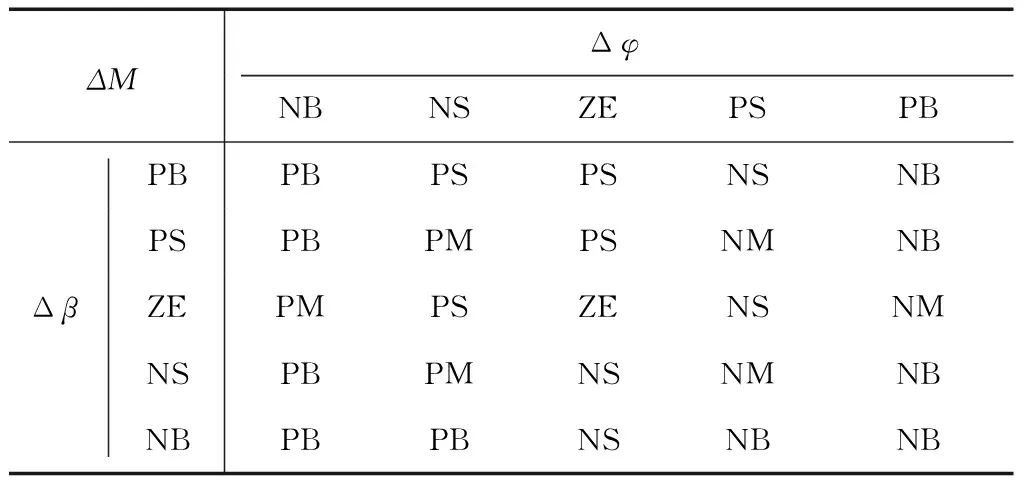
表1 模糊规则

4 系统仿真验证

基于上述分析，为验证文中提出的基于MPC和模糊控制的智能汽车路径跟踪方法在高速工况下的实用性，搭建CarSim/Simulink联合仿真模型进行仿真路径跟踪仿真.文中追踪的路径为文献[8]中的避障路径，汽车理想行驶轨迹和理想横摆角表达如下.

(12)

(13)

式中:yd为车辆换道后的侧向位移;xd为车辆换道后的纵向位移.

现设置如表2所示高速工况进行避障仿真.

表2 仿真工况

工况一的仿真结果如图4～6所示.

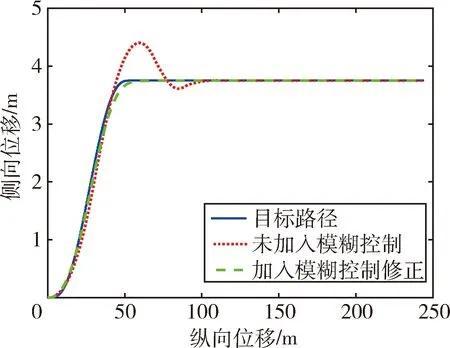
图4 行驶轨迹对比图

在工况一中，由图4和图5可以直观地看出，在较高速工况下，与未加入模糊控制相比，基于MPC控制策略的车辆在加入模糊控制修正后，行驶轨迹曲线更加贴合目标路径轨迹，横摆角也更加贴近理想曲线；由图6中的纵向位移偏差对比图可知，加入模糊控制后，偏差得到可观减少(误差值最多可修正0.63 m)且最大偏差仅为0.18 m左右，表明经过模糊控制修正后，车辆路径跟踪效果良好，跟踪精度较高.

图5 横摆角对比图

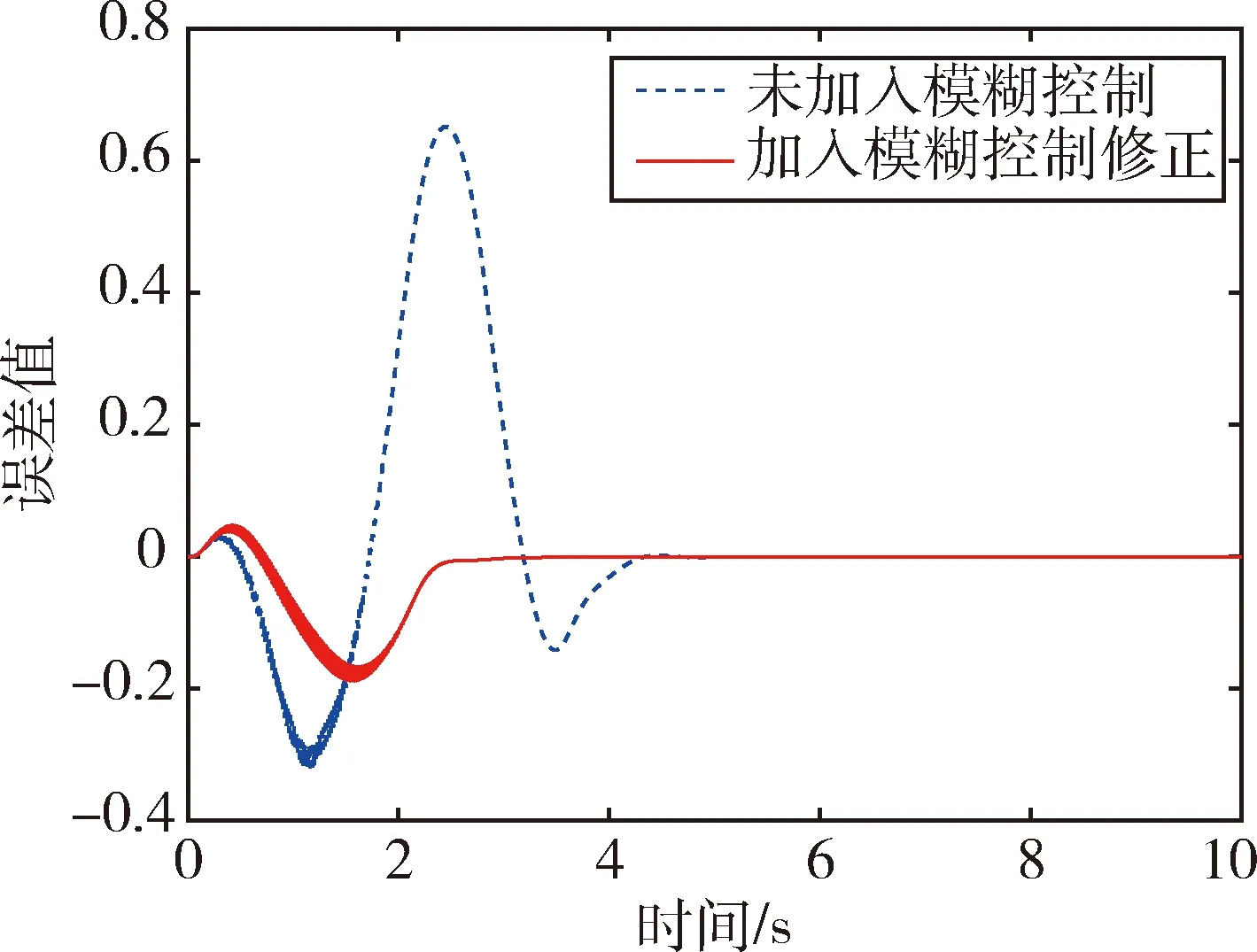
图6 纵向位移偏差对比图

工况二的仿真结果如图7～9所示.

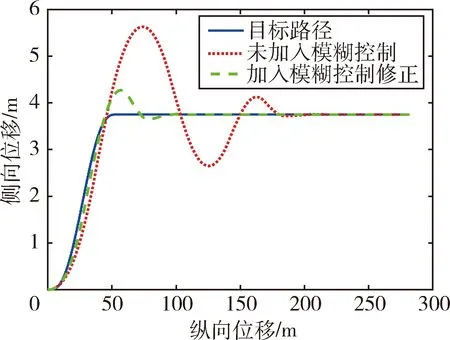
图7 行驶轨迹对比图

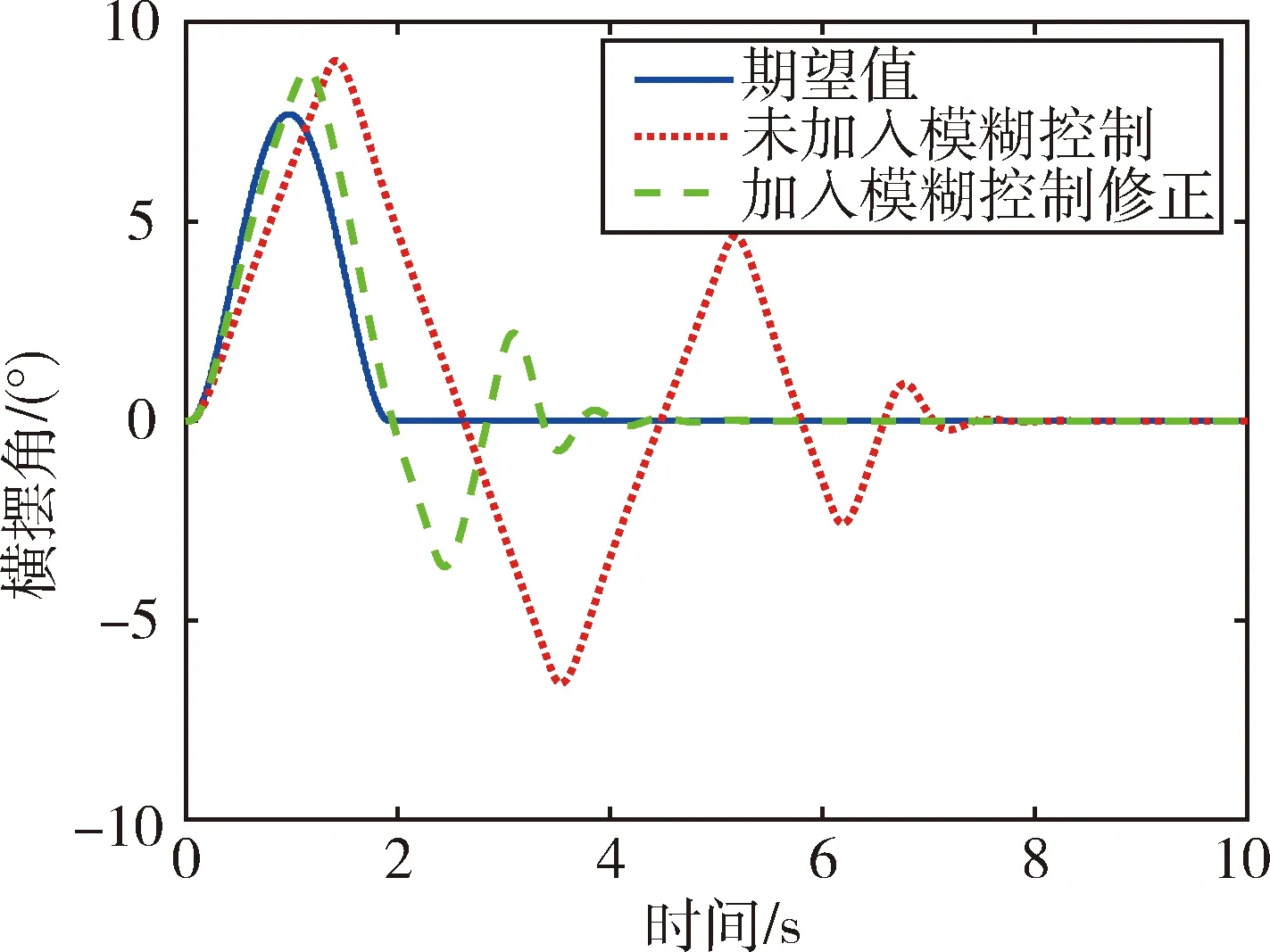
图8 横摆角对比图

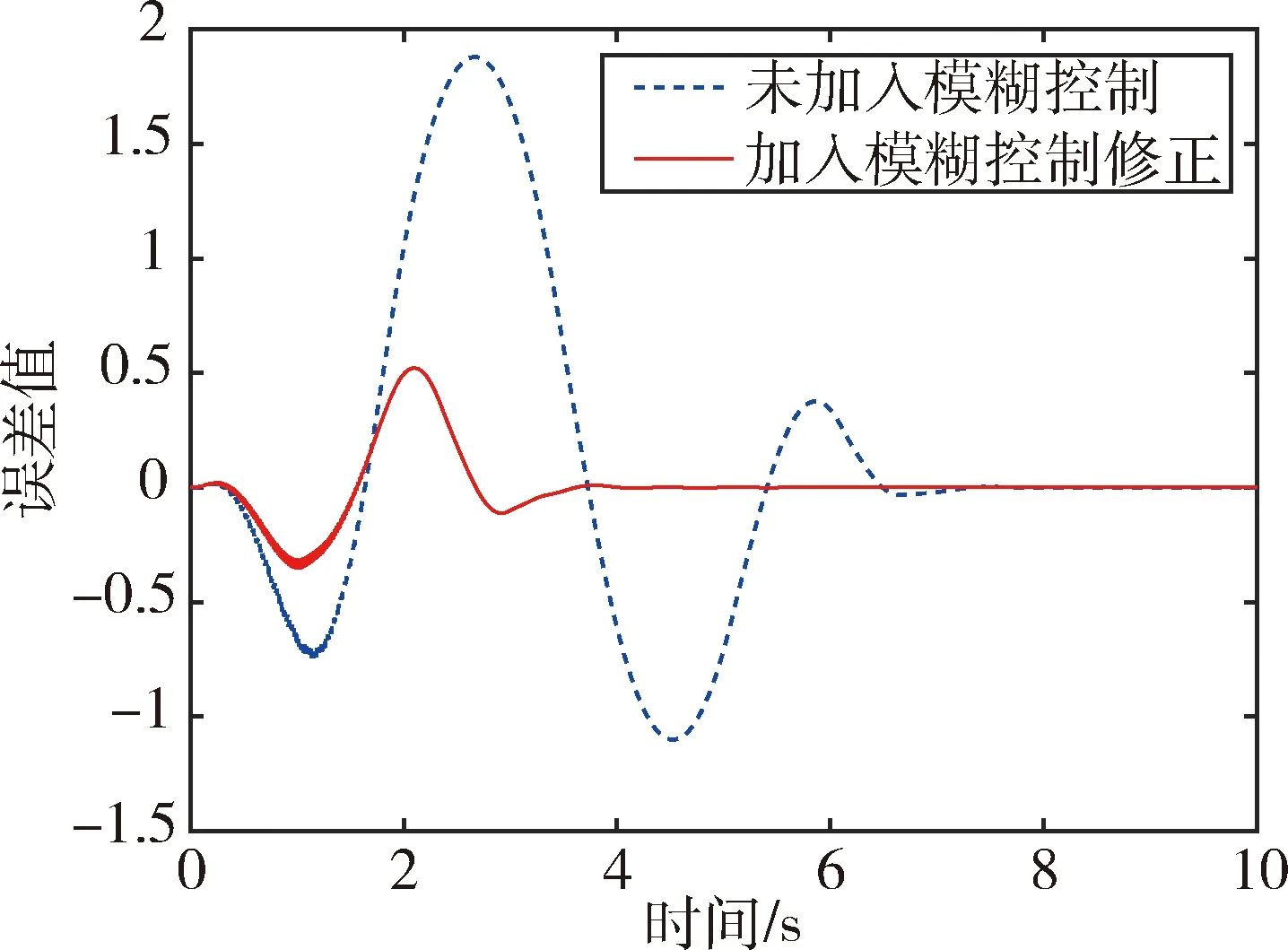
图9 轨迹偏差对比图

工况二为高速工况，由图7和图8可以直观地看出，在110 km/h的高速工况下，与未加入模糊控制相比，基于MPC控制策略的车辆在加入模糊控制修正后，行驶轨迹和横摆角均更加贴近理想曲线；由图6中的纵向位移偏差对比图可知，加入模糊控制后，偏差得到可观减少，最大偏差为0.5 m左右，表明在高速工况下经过模糊控制修正后，车辆路径跟踪效果良好，跟踪精度较高.

5 结 论

文中针对高速转向工况下智能汽车路径跟踪偏差较大的问题，设计了基于MPC和模糊控制的智能汽车路径跟踪策略，基于MPC算法进行路径跟踪可以有效解决诸多非线性约束的问题，实时性较好；模糊控制器以输入量质心侧偏角误差Δβ和横摆角速度误差Δφ为双输入，设计模糊规则，输出额外的横摆力矩ΔM施加至车轮，从而减少轨迹的偏差.通过Matlab /Simulink软件与Carsim软件联合仿真验证可知，在自车以中高速(85 km/h)和高速(110 km/h)行驶进行避障轨迹追踪时，加入模糊控制器后，轨迹偏差均得到了客观较小，提高了跟踪精度，路径跟踪效果良好.