基于流场载荷的液力变矩器涡轮毂拓扑优化

王嘉轩， 刘 城,2

(1.北京理工大学 机械与车辆学院，北京 100081；2.北京理工大学 重庆创新中心，重庆 401122)

液力变矩器是自动变速系统中的核心部件，具有优越的自适应性、无级变速变扭、减振隔振等特点.闭锁式液力变矩器加装单向联轴器和闭锁离合器，能够提高高速比下的效率.但是，此类闭锁式液力变矩器结构复杂、重量大，涡轮毂在牵引工况、闭锁工况下受力状态变化大，为进一步提高车辆动力性及响应特性，文章针对闭锁式液力变矩器涡轮毂开展轻量化设计.

现阶段液力变矩器优化设计主要以循环圆和叶栅系统为对象，优化工作主要就扁平率、过流比面积、流道收缩率以及叶片角度、叶片个数、叶片偏转角等叶栅系统参数展开[1-6].轻量化方法在液力变矩器的优化设计中大多应用在叶栅系统上.闫清东等[7]对叶片厚度进行了全因子试验，研究了叶片厚度对变矩器经济性和动力性的影响规律，开展了叶片厚度多目标优化设计并加以实验验证，有效改善了变矩器性能.魏巍等[8]对液力变矩器内部流场进行了数值模拟计算，并利用单向流固耦合技术研究了不同叶片厚度对变矩器转矩和叶片结构强度的影响，探索了叶片厚度减薄的轻量化潜力.马珂婧等[9]基于响应面法和正交试验法对涡轮叶片进出口角以及各叶片厚度进行了优化设计，结果显示响应面法能够获得厚度更薄、性能更好的叶片造型.刘博深等[10]基于流固耦合对叶栅厚度开展轻量化设计，搭建了叶栅厚度优化设计平台，研究了不同叶栅厚度对起动转矩的影响规律并进行了实验验证，能够在保证动力性的条件下有效减重.通过上述分析可知，在液力变矩器轻量化设计研究中，鲜有针对结构件进行的减重设计，拓扑优化作为一种机械优化设计的常用方法并没有在液力变矩器轻量化设计方面得到广泛应用.

拓扑优化能够在设计域内求解最佳的材料分布，其结果对零件造型具有较好的指导意义.连续体拓扑优化以均匀化方法为理论基础，逐渐发展出变密度法、水平集法、相场法和渐进结构法等方法.其中，基于SIMP插值的变密度法概念清晰、简便，迭代稳定，优化效率高，在工程中得到了广泛应用[11].

研究基于ANSYS Workbench平台，以直径为430 mm的液力变矩器为对象，建立其全流道模型，对内部流场进行瞬态CFD仿真计算，以得到各速比下的叶轮转矩.建立涡轮毂有限元模型，以流场载荷和装配关系为边界条件，以柔度最小为设计目标，以质量为约束条件，采用SIMP插值的变密度法对其进行拓扑优化，得到最佳材料分布，实现对结构件的轻量化设计.

1 液力变矩器流场数值模拟

1.1 全流道模型和流场计算前处理

液力变矩器循环圆直径为430 mm，采用三维造型软件UG，提取变矩器全流道模型.用四面体非结构性网格对变矩器全流道模型进行离散化处理，在泵轮转速、涡轮转速、导轮静止的起动工况，建立不同网格尺寸的CFD计算模型、进行网格无关性分析.当不同网格尺寸下对应的泵轮转矩相对误差值小于3%时，可以认为该尺寸下的计算结果独立于网格密度.网格无关性验证结果如图1所示，最终确定整体网格尺寸为1.8 mm，整体网格数量约为2 100万.

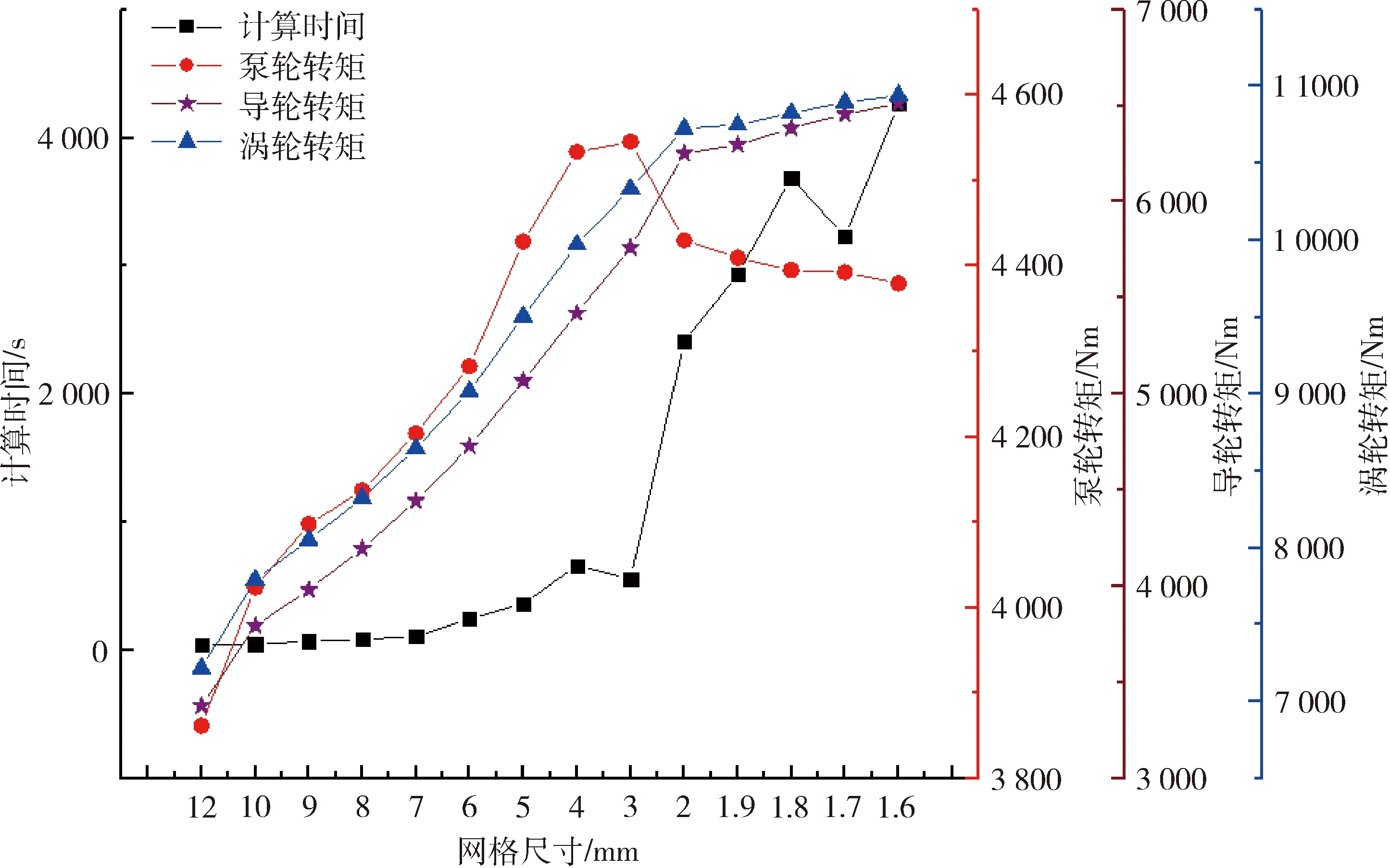
图1 CFD网格无关性验证

1.2 全流道瞬态流场计算

涡轮毂与涡轮通过传力销相连，其载荷主要来源于涡轮转矩，因此，通过流场数值模拟求得涡轮转矩时，均值即可得到涡轮毂的载荷边界条件.通过液力变矩器与发动机的匹配，在实际使用过程中，泵轮转速最高能够达到3 400 r/min，此时，涡轮毂上的载荷也相应达到最大值.由于受到实验条件限制，无法通过实验获得变矩器高转速下的液力特性，故采用ANSYS CFX对变矩器进行流场数值模拟.为准确反映液力变矩器内部由于叶轮相对运动导致的瞬态效应对流场的影响，进行液力变矩器全流道瞬态流场计算.

CFD计算时，设置泵轮转速为np=3 400 r/min，速比分别为i=0，0.1，0.2，…，0.8，导轮静止不动.参考压力为0.4 MPa，交界面模型采用瞬态转-静子法模型，湍流模型采用k-ε模型.流场求解的对流项数值离散格式采用高精度格式，时间步长为10-4s，每个时间步内最大迭代次数为6次，当压力和流速的均方根误差小于10-5时，认为达到精度要求.为加快收敛速度，瞬态计算以对应速比下的稳态计算结果为初值.

在泵轮转速np=2 000 r/min的条件下，验证CFD计算模型的准确性.由图2可知，CFD模型能够较好的反应各工况下变矩比、泵轮扭矩系数和效率的变化趋势，且具有较高精度.

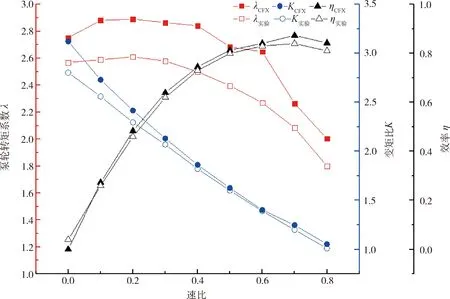
图2 液力变矩器原始特性曲线对比图

2 涡轮毂拓扑优化设计

基于ANSYS Workbench对涡轮毂开展稳态仿真分析以得到其应力分布，进而在此基础上进行拓扑优化.

2.1 中间密度插值模型SIMP

该方法假设材料单元的相对密度xi为[0,1]之间的连续变量，建立一种材料属性(如弹性模量)和单元相对密度之间的函数关系，并认为泊松比μ为不随密度变化的常量.相对密度xi的取值对应单元的保留状态，当xi=0时,对应单元被去除；xi=1时,该单元被保留.中间密度插值模型可以近似表示为[12]

E(xi)=(xi)pE0，

(1)

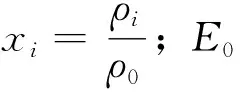
一般当材料的泊松比ν≥0.3时，p=3的解在理论上可行.如图3所示，xi和p共同决定材料单元的弹性模量向E0的逼近程度.

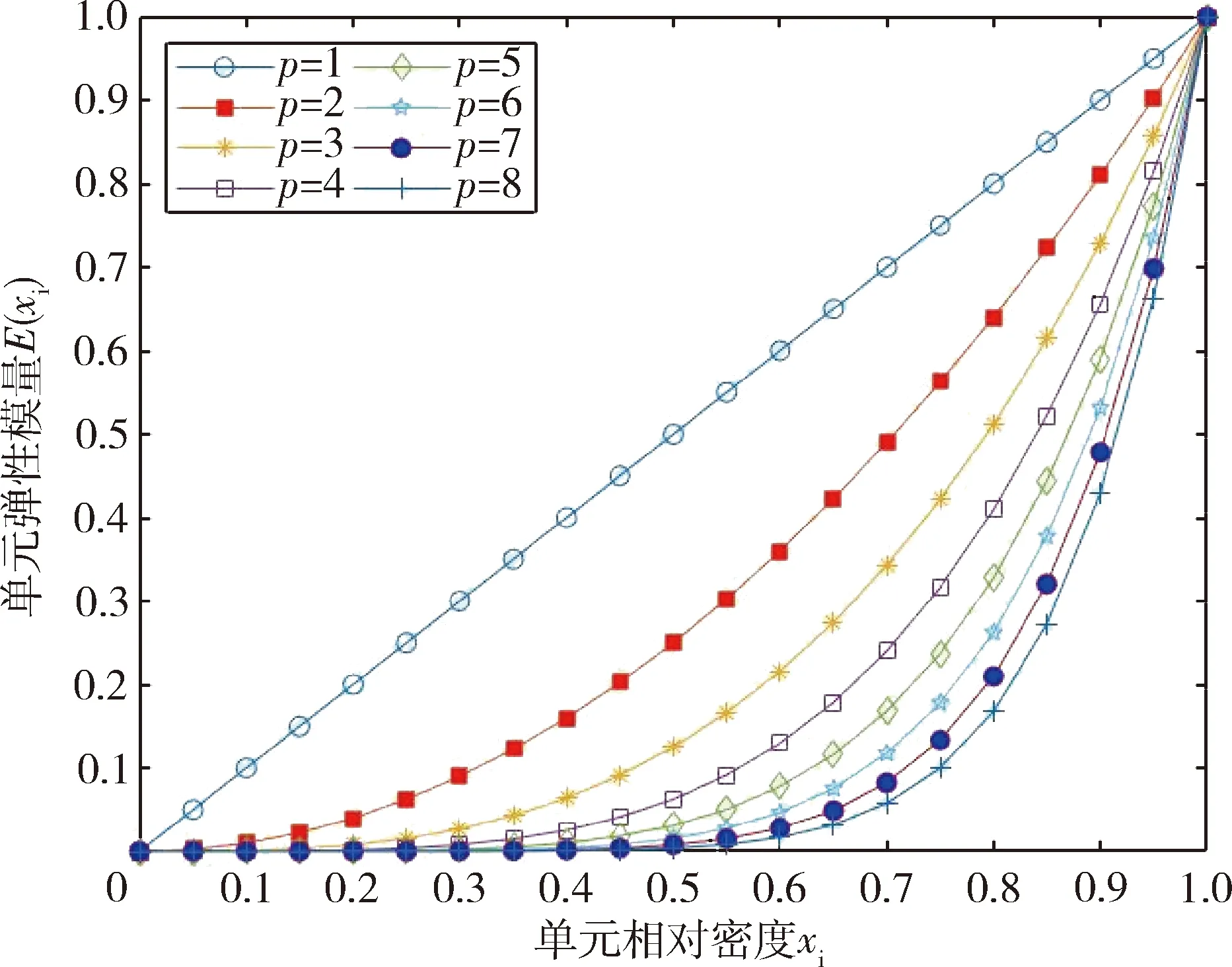
图3 相对密度与弹性模量关系图

以结构件的刚度C为优化目标，以优化前后体积比为约束条件，建立基于SIMP插值的变密度法拓扑优化数学模型为[13]

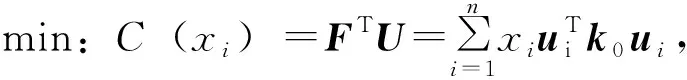
(2)

式中:vi为单元相对体积；V0和V分别为优化前和优化后设计域的体积；V*为约束体积；f为优化体积比.

2.2 液力变矩器总成结构分析

液力变矩器结构总成如图4所示.闭锁离合器外壳通过花键和主动齿轮连接，通过普通螺栓与泵轮连接.涡轮毂上有传力销孔和螺栓孔，用来与涡轮连接并传递转矩，同时制有内花键与输出轴相连以输出转矩.涡轮毂外圈的外花键上套有摩擦片.导轮座用来支撑导轮和泵轮座，同时还作为单向离合器的内圈，在变矩工况下和滚子一起将外圈锁止.

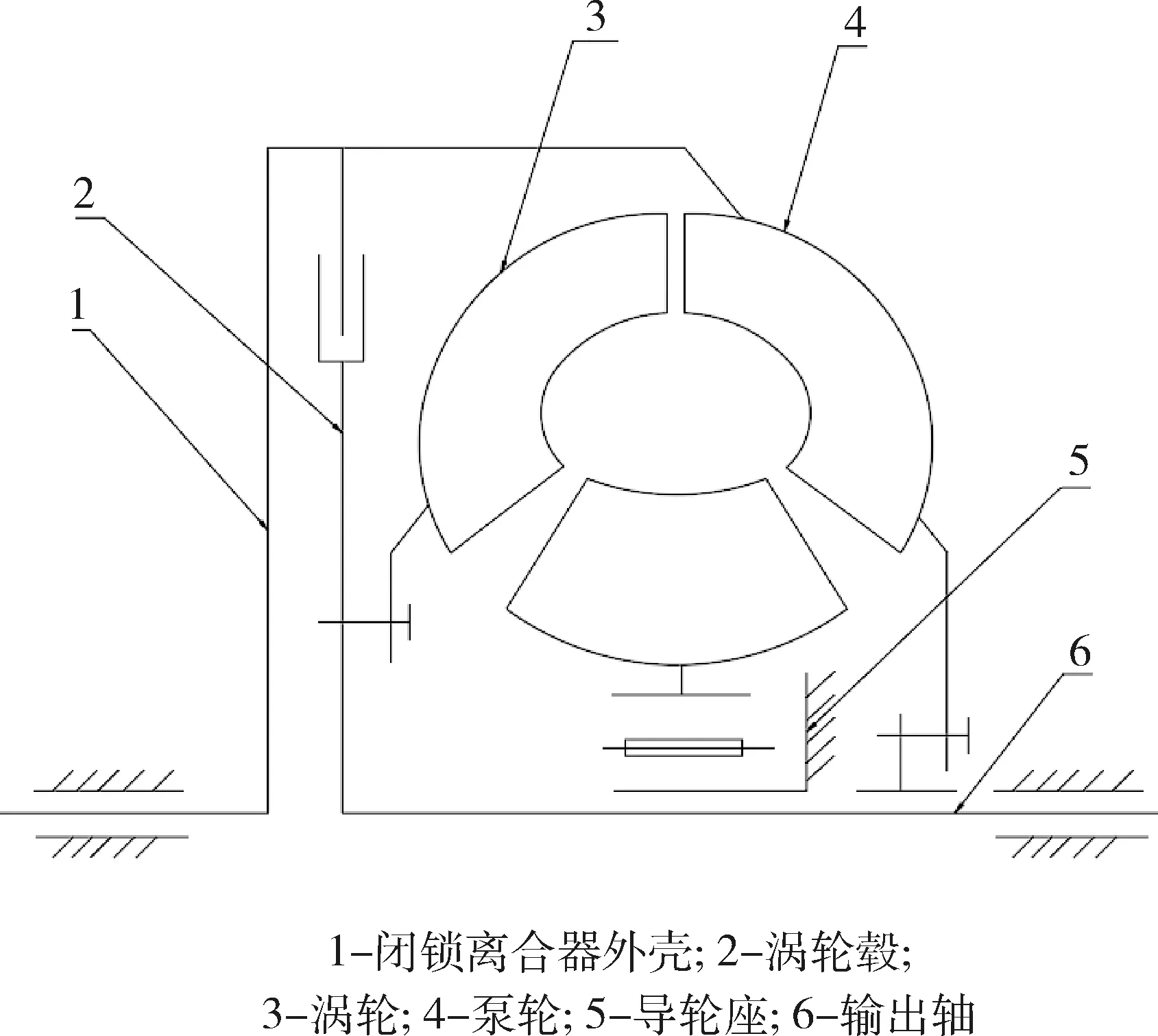
图4 液力变矩器总成结构简图

图5为液力变矩器变矩工况和闭锁工况下的功率流.液力变矩器工作在变矩工况时，功率从发动机输出端输出，经由前传动从主动齿轮处输入变矩器总成，经过闭锁离合器外壳、泵轮、涡轮传至涡轮毂，最后通过输出轴输出.变矩器工作在闭锁工况时，高压控制油推动活塞压紧摩擦片，从而将泵轮和涡轮连为一体，功率从主动齿轮输入后，直接经过闭锁离合器、摩擦片传至涡轮毂并从输出轴输出.

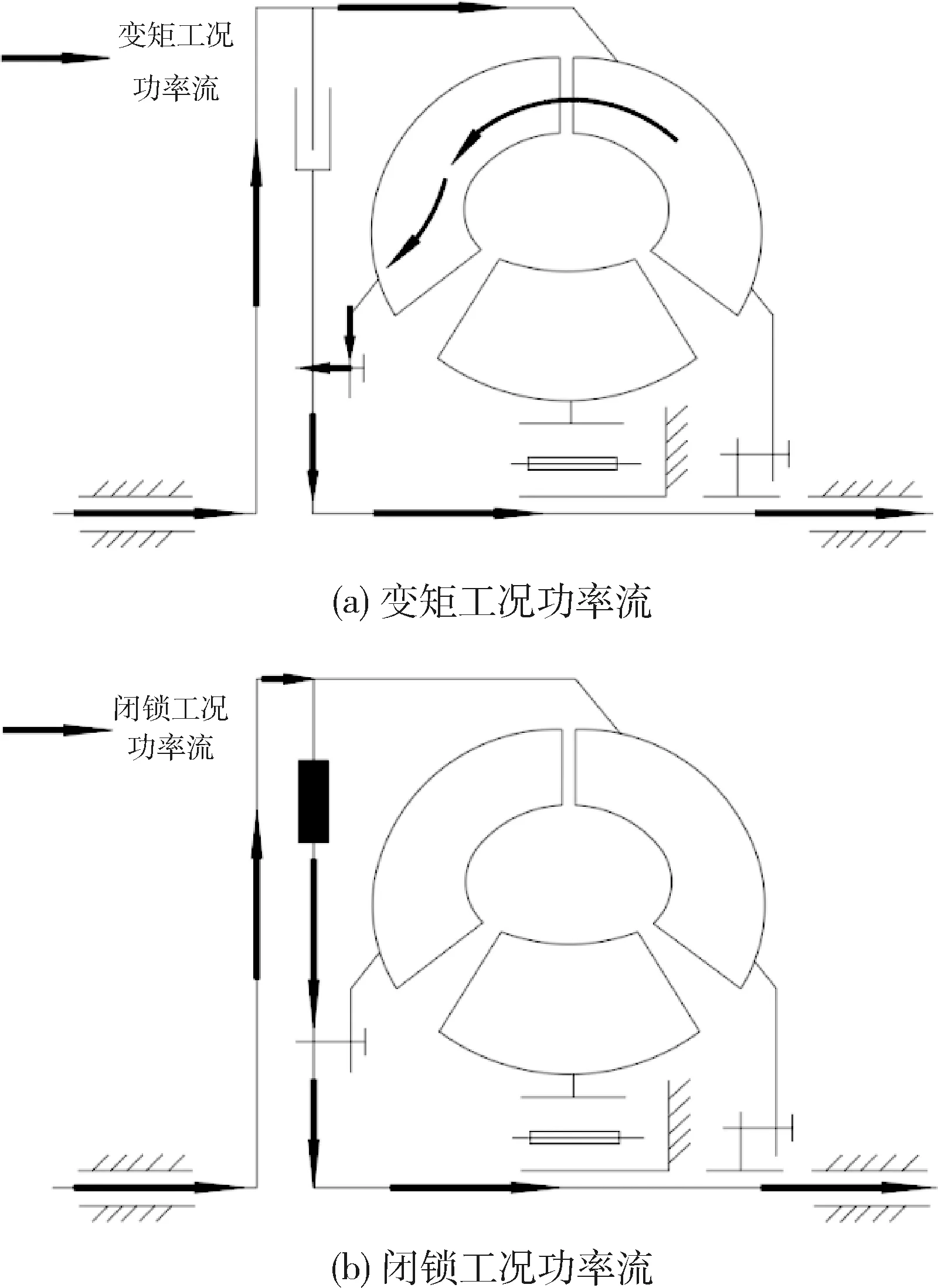
图5 液力变矩器功率流

通过上述分析可知，涡轮毂是变矩工况和闭锁工况中传递功率流的关键结构件，因此，优化设计主要针对该结构件展开.涡轮毂的几何模型如图6所示.几何模型对实际模型做出了适当简化以提高计算速度，用光轴代替内、外花键，用光孔代替螺纹孔，并且将不影响应力分布的倒角和圆角改为直角.

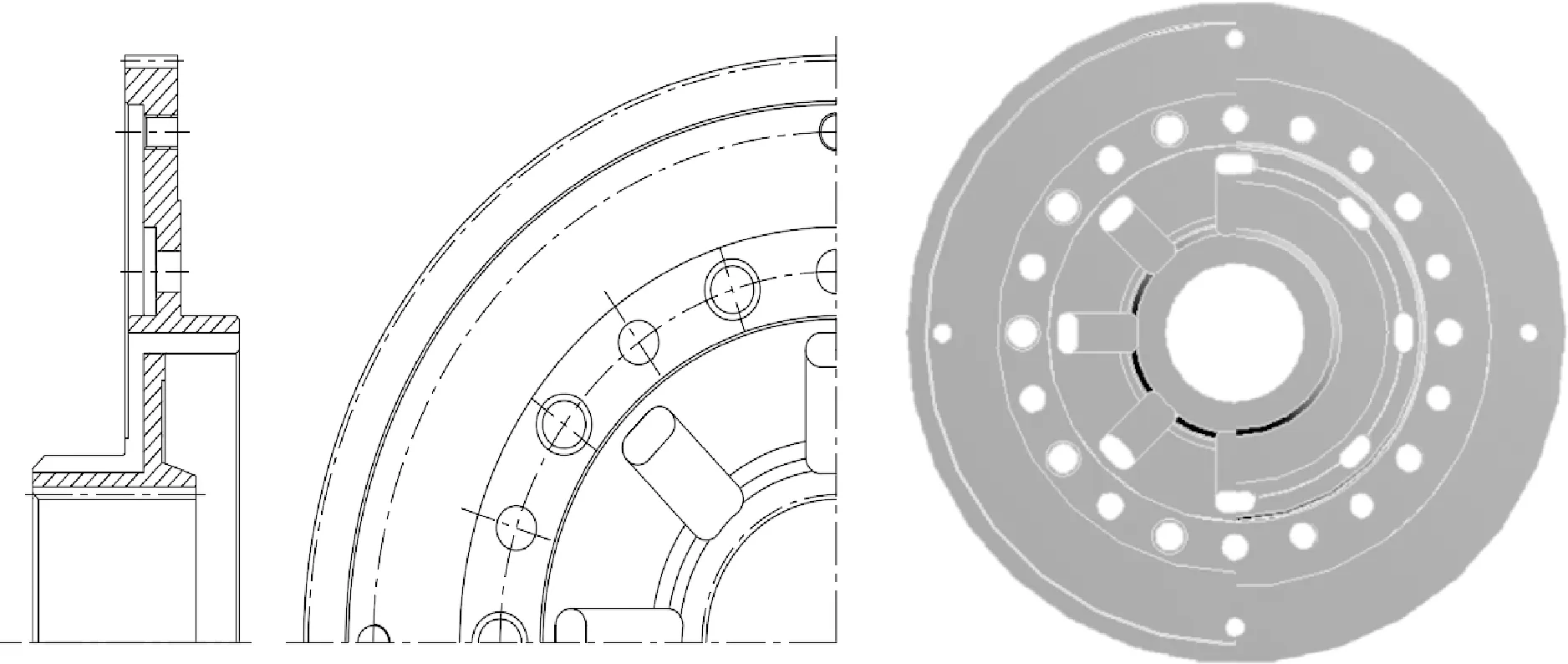
图6 涡轮毂几何模型

2.3. 拓扑优化条件设置

2.3.1 起动工况条件设置

首先对涡轮毂开展网格无关性分析，如表1可知，当单元总数在76.6万以上时，可保证最大应力独立于网格密度.采用四面体单元对涡轮毂进行网格划分，全局网格尺寸为2 mm，局部用0.1 mm网格进行加密.

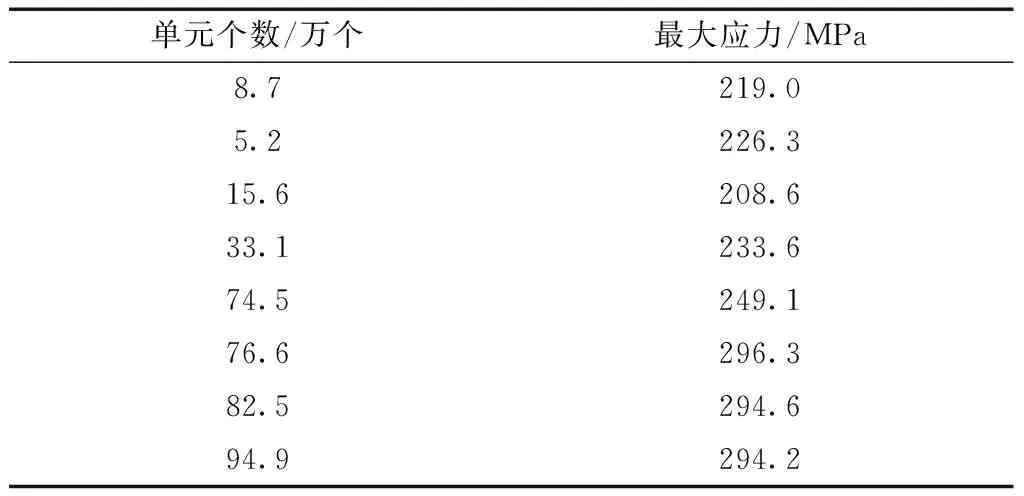
表1 涡轮毂网格无关性分析

在起动工况下，闭锁离合器脱开，摩擦片不工作，因此，涡轮毂的载荷主要来自涡轮的转矩，通过10个φ14的传力销加载.涡轮毂通过花键和输出轴相连，因此，将花键处设置为固定约束.起动工况下涡轮静止，因此，无需为其添加角速度.静力学分析边界条件如图7(a)所示.

从图4可知，涡轮毂与涡轮、输出轴、摩擦片等零件之间存在装配关系，因此，将这些区域定义为非设计域(图7(b)非设计域)，设计域为螺栓孔和外花键之间的区域(图7(b)设计域).

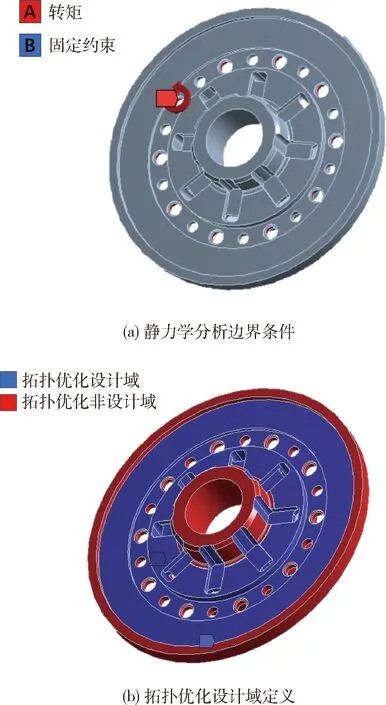
图7 起动工况涡轮毂边界条件

涡轮毂是圆周对称结构.为了使拓扑结构也具有圆周对称性，在约束中添加圆周对称制造约束，对称数量为3.以柔度最小为目标，为突出造型特点以体积减少为原重50%为约束条件进行优化，求解方法采用优化准则法，默认迭代次数500 次.设置去除材料的相对密度阈值为0.5.

2.3.2 闭锁工况条件设置

在闭锁工况下，闭锁离合器摩擦片接合，使涡轮和泵轮转速相同，变矩器由液力传动变为机械传动.因此，涡轮的载荷主要是作用在外花键上的闭锁转矩，相应地要将转矩的作用位置定义为拓扑优化的非设计域，同时还要考虑离心力的影响.在前处理中，发现工艺孔对应力分布结果影响较小，因此，在该工况下，将其略去，以提高拓扑优化结果在结构上的完整性.对结构件施加对称约束，保证拓扑优化结果的圆周对称性.边界条件的定义如图8所示.以柔度最小为目标，体积减少为原结构75% 为约束条件进行拓扑优化.

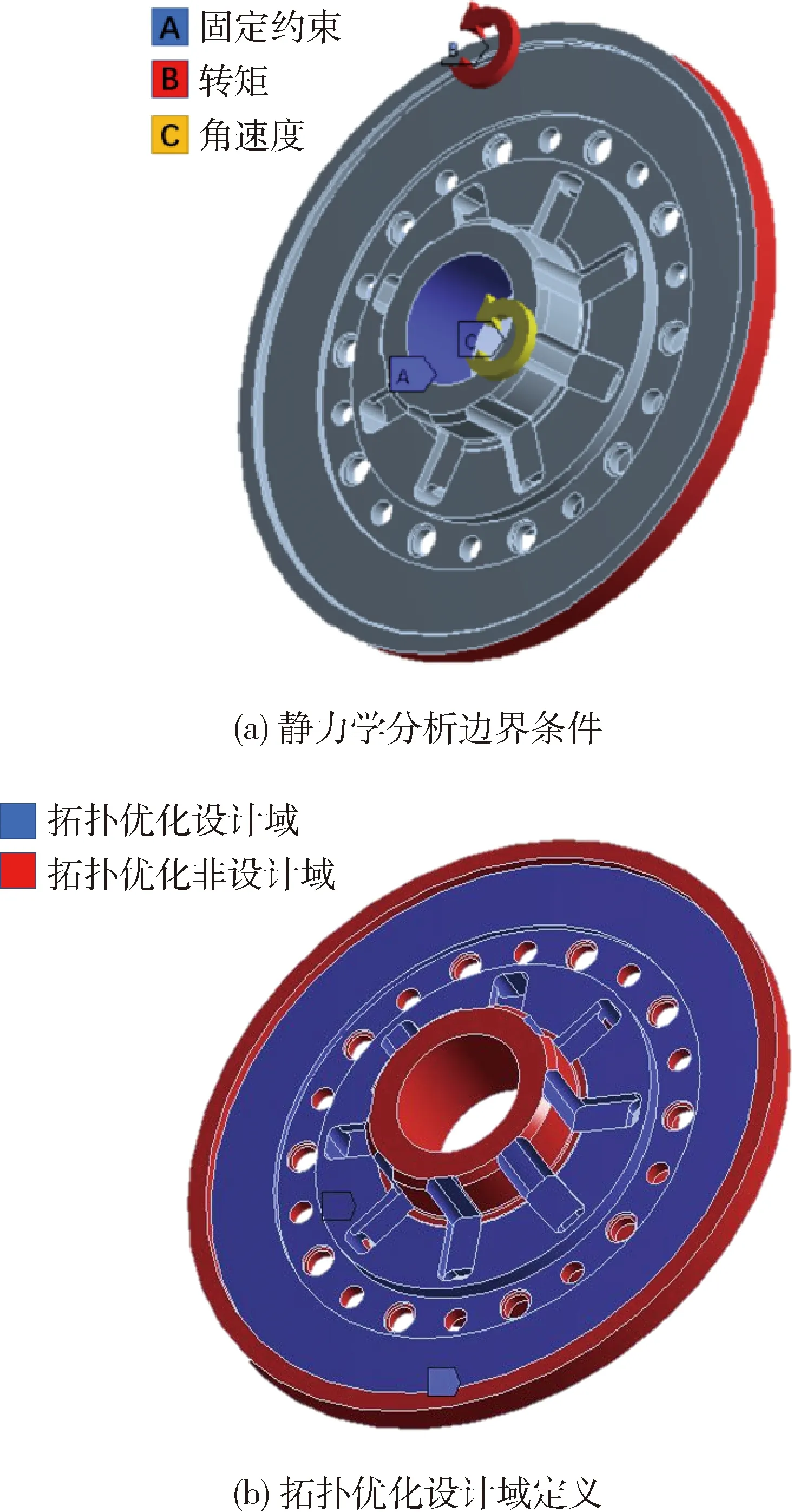
图8 闭锁工况涡轮毂边界条件

2.4 拓扑优化结果

2.4.1 起动工况拓扑优化结果

拓扑优化密度云图如图9所示，外花键齿根到传力销之间的材料几乎全被去除.这是因为在这种工况下摩擦片未接合，所以，外花键与传力销之间的结构载荷很小，主要承载区域在传力销到内花键之间.因此，去除材料的区域与理论分析是相符的.但是,在优化过程中，优化算法仅仅考虑了对传力路径上的材料进行重新分布，却忽视了结构件的完整性.仅凭单一工况下的拓扑结果难以确定最终的优化方案.

图9 起动工况涡轮毂拓扑优化结果

2.4.2 闭锁工况拓扑优化结果

对闭锁工况下的涡轮毂开展拓扑优化，密度云图如图10所示，可见在该工况下涡轮毂造型上有较大冗余.优化主要集中在外花键与传力销之间的区域，结果显示应减小该处厚度，并且形成轮辐式结构，其旋向和载荷转矩方向一致，具有很强的对称性，同时还应注意到，辐条的数量受到圆轴对称约束的影响.除此之外，涡轮毂中与涡轮及轴承具有装配关系的部分受力区域中的实体材料被去除，形成中空结构，这与工程实际不符，模型重构时不予以考虑.

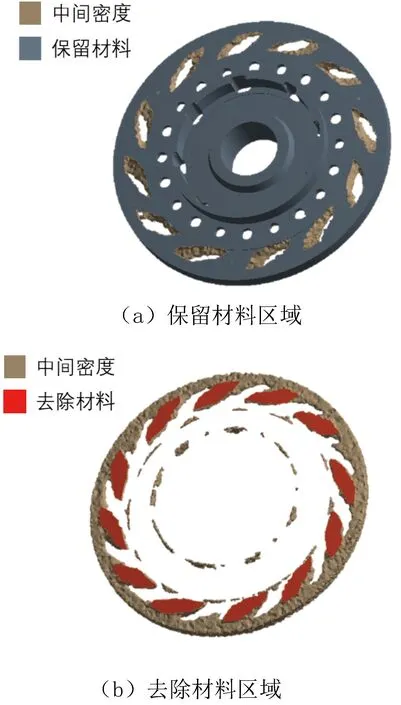
图10 闭锁工况拓扑优化结果

2.4.3 涡轮毂优化方案

从上述优化结果可知，两种工况下的拓扑优化都针对外花键和传力销孔之间的材料进行了重新分布，并且闭锁工况下的优化结果能够满足起动工况下的优化结果，因此，优化方案取二者的交集，最终提出两种优化方案,如图11所示.

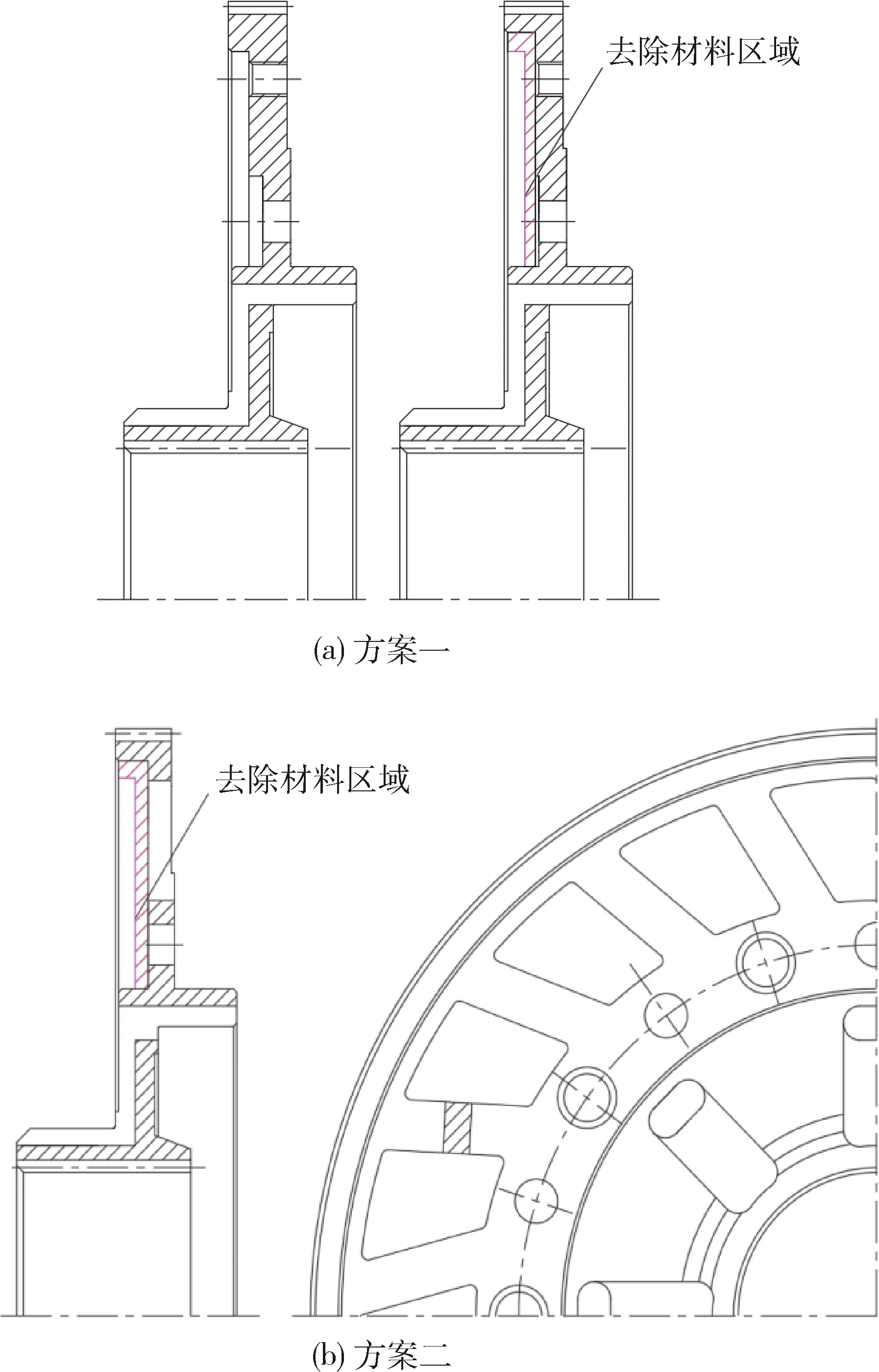
图11 涡轮毂优化方案对比

方案一舍弃了类似加强筋的结构，能够保证制造性，却无法满足材料的最佳分布；方案二采用轮辐式结构，能够较为准确地反映拓扑优化的结果，但零件可制造性较差，在这种情况下，涡轮毂优化结果的制造性与最佳材料分布是相互制约的，优化前后结构件性能对比如表2所示.方案一和方案二的减重比例分别为15.3%和25.1%

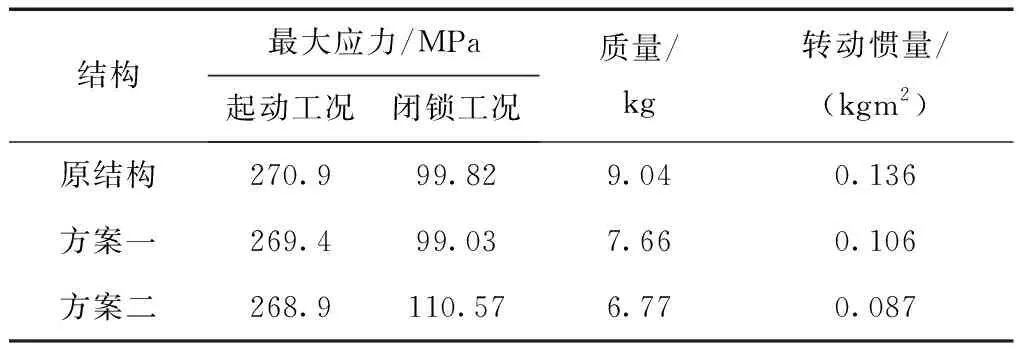
表2 优化结果和原结构对比

3 结 论

文章采用基于SIMP插值的变密度法对液力变矩器的涡轮毂展开了基于流场载荷的拓扑优化，得到了如下结论：

1)采用ANSYS Workbench对涡轮毂进行拓扑优化，在保证安全系数基本不变的前提下能够达到较好的减重效果，减重比最高可达到25.1 %.以柔度为目标，体积为约束条件，采用优化准则法求解的变密度法拓扑优化迭代速度较快，对连续体的拓扑优化能够取得较为满意的结果；

2)涡轮毂具有多工况、多配合关系的特点，其可制造性和最优材料分布相互制约，此结论可以为涡轮毂的造型设计提供一定参考；

3)基于SIMP的拓扑优化结果具有较强的指导意义，但其结果受到网格密度影响较大，且会出现与工程实际不符之处，在模型重构阶段，需要合理解读拓扑优化密度云图，结合工程实际对优化结果进行取舍，兼顾结构件的性能和制造性.