基于极限学习机与振动响应的路面辨识技术研究
2022-07-01付晓易赵玉壮
付晓易, 赵玉壮, 王 媛
(1.北京理工大学 机械与车辆学院,北京 100081;2.北京汽车集团越野车有限公司,北京 101399)
车辆行驶过程中,实时准确地获取当前的路面类型,并依此调节动力系统响应、车身姿态控制等车辆子系统关键特性,可为车辆高速机动性、操纵稳定性及行驶平顺性等性能改善提供重要参考.因此,如何准确快速地获取当前路面信息是优化车辆控制的重要基础.当前车辆智能化程度越来越高,硬件平台也越来越容易为复杂多样的算法提供坚实的基础.
目前,基于图像与车辆振动信号进行路面辨识各有特点,图像具有较好的预测前瞻性,但是抗干扰能力差,受光照、烟尘或水雾影响较大,并且设备相对昂贵;振动信号虽然不具备前瞻性,但是环境鲁棒性好,数据处理手段较多.董锴等[1]对道路交通路面性能选定路面状况指数、错台指数、平整度指数、脱空指数、抗滑性能指数作为评定指标,建立起优、良、中、差4个评价标准;王红岩等[2]为提高车辆虚拟试验结果的准确性,对车辆行驶路面数字化建模方法进行了研究采用谐波叠加法建立了三维随机路面模型,通过与实测数据作功率谱密度对比,表明二者具有较好的一致性,验证了三维随机路面模型的可信性;赵凯等[3]提出将时域参数特征和小波包能量特征相结合的特征提取方法,利用概率神经网络对地面进行分类;谷盛丰等[4]针对应用径向基神经网络识别路面不平度的输入选择、输入方案确定和识别效果评价3个问题,提出了一种解决方法;刘秋等[5]利用图像进行了半主动悬架上基于卷积神经网络的路面识别;王志红等[6]将机器视觉中较为流行的语义分割模型作为基础模型,同时改进模型输出网络,提出一种新的路面类型识别技术,辨识精度可达94%左右.
本文设计了一种基于振动数据的行驶路面工况辨识系统,利用某6×6中型越野车辆的悬架动挠度、车身垂向加速度和俯仰角速度为路面辨识振动信号依据,分析对比了ELM与SVM两种辨识算法的辨识精度与实时性,并探讨了数据预处理方式对辨识精度的影响规律,通过选取合适的统计特征与数据计算方式,提高基于振动数据的行驶路面工况辨识精度.
1 分类机原理
1.1 ELM简介
极限学习机是一个前向传播的单隐含层神经网络,其结构如图1所示.
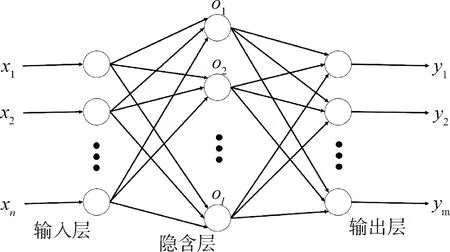
图1 ELM网络模型
输入层样本每一个参数xi与隐含层每个神经元Oj均有连接权值ωij,该权值随机产生,共同组成输入层连接权值矩阵Ω.同理,隐含层与输出层有输出层连接权值矩阵B,该矩阵将由解方程获得.当获得训练样本输入矩阵X与输出矩阵Y,便可由式(1)求得隐含层的输入矩阵H,再选取合理的激活函数—常用的有Sigmoid函数和径向基函数—激活H,即得隐含层的输出T,最后可由式(2)解得B,从而确定该学习机的结构.
ΩX=H,
(1)
B=T+Y,
(2)
式中:T+代表T的伪逆矩阵,可以通过岭回归等方法求得[7].
由于该模型不需要任何迭代计算,所以,训练速度会非常快,并且待定参数也只有神经元个数与激活函数两个,使用简单便捷.
1.2 SVM简介
支持向量机是以统计学的VC维理论为依据,在极小的结构风险性原则下,进行的一种机器理论的计算方法.实际过程是利用核函数将低维线性不可分的数据,映射到高维空间求解凸二次规划,得到一个超平面将数据区分开.
如图2所示的二分类问题,圆为正类{x,1},方块为负类{x,-1},则这组数据被直线(超平面)式(3)线性分割.
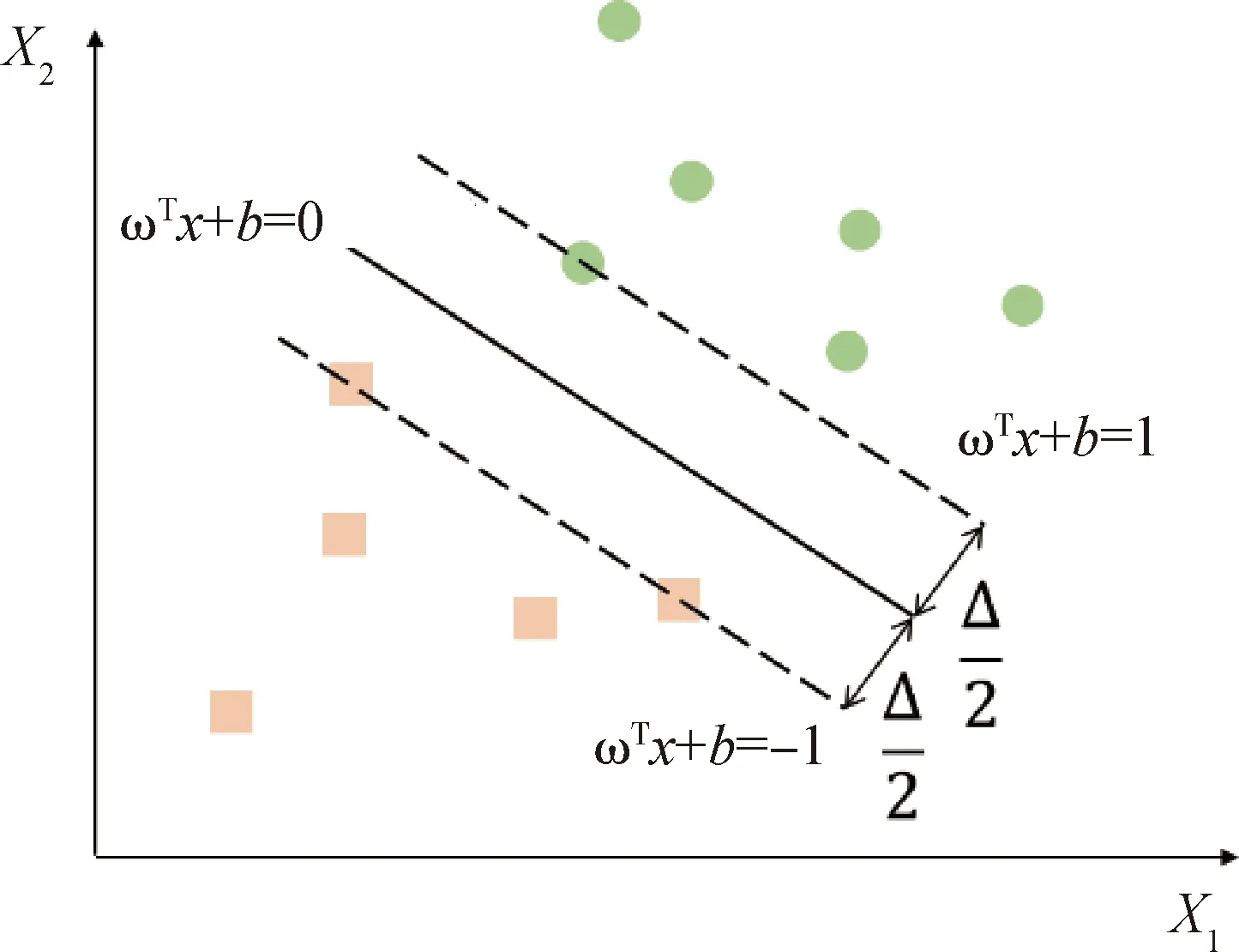
图2 二分类示意图
ωTx+b=0.
(3)
显然对于这组数据有无数条直线可以将其分开,设Δ为两种类别各组平行的边界线之间的距离,其最优解就是Δ最大时的超平面,两条虚线间的距离可由式(4)算得.
(4)
为使距离最大,最后即化为式(5)所示的不等式约束下的最优化问题.
(5)
由于本问题是不等式约束下的二次优化问题,所以,在KKT(Karush-Kuhn-Tucker)条件下使用拉格朗日乘子法[8],即可求解该问题.最后,搭配核函数可以利用SVM对线性不可分问题进行分类.
1.3 学习机对比
(1)ELM只需一次性求解即可获得分类机,比SVM迭代寻优快很多.
(2)ELM对样本个数敏感,样本数量不同,分类结果差异较大,SVM辨识结果随样本数量变化平缓.
(3)ELM等传统神经网络当样本维数过多时,训练时长显著上升,SVM则可以避免维数灾难.
2 试验研究
2.1 辨识信号选取
机器学习样本各个维度的数据是由车辆采集的信号计算得到的,因此,选取仿真输出数据时,既要考虑车辆自身因素,同时也要考虑对机器学习算法的影响与适应性,通常参考以下原则:
(1)优先选取对路面激励敏感,并且受其他如驾驶操控或环境因素等非路面工况影响较小的量;
(2)保证数据高性能的同时也要考虑数据获取的难易程度与经济性,不仅满足仿真平台的要求,还要为实车装备准备;
(3)选取数量合适的参数,使得机器学习算法实现速度与精度的最佳匹配.
2.2 试验平台与方法
试验选用某6×6中型高机动越野车,质心处布置有VT905微机械陀螺,采集俯仰角速度及质心垂向振动加速度;悬架系统布置有位移传感器,采集悬架动行程.试验车辆以30 km/h稳定车速行驶于公路、砂石路和越野路.数据采集系统采样频率为100 Hz.
图3为传感器测得的不同路面悬架动挠度,公路工况响应曲线与砂石路和越野路工况响应曲线在速度与幅值上均有明显差异.
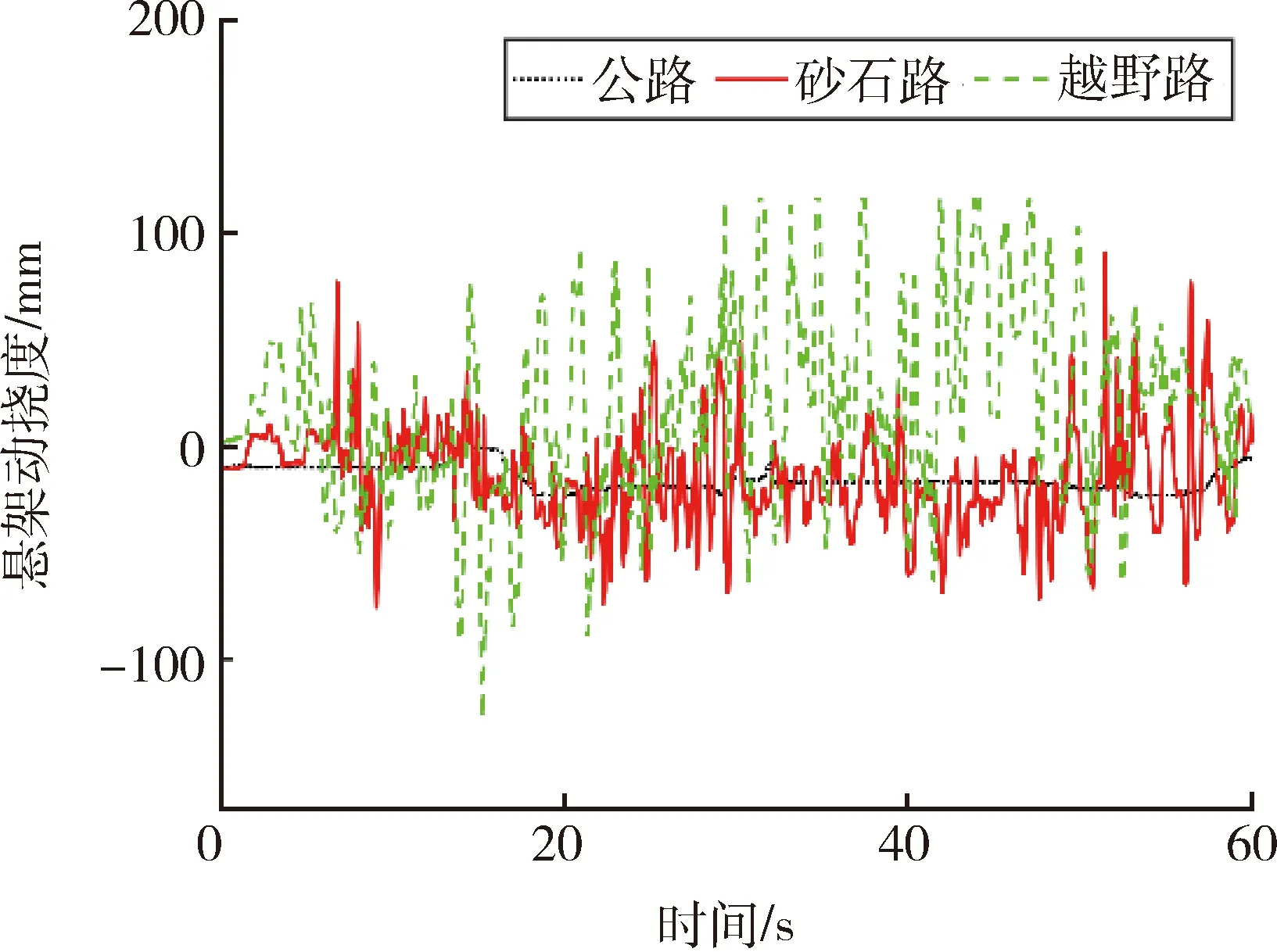
图3 悬架动挠度信号原始值
因此,基于振动响应路面分类的依据是:首先,根据国家标准路面或经验需求将路面划分等级或种类;然后,采集行驶车辆在指定路面的振动响应;最后,将提取信号的原始值或统计值输入分类器完成训练.
2.3 数据处理
对原始数据进行预处理,常用的统计量有均值、均方根、峭度、歪度等,前两者可以体现信号的绝对水平,后两者则体现信号的概率密度.试验选取均方根值与峭度作为典型,二者计算公式如式(6)、(7)所示.
(6)
(7)
式中:n是样本容量;μ为样本均值;σ为样本标准差;E为期望.
由于上述统计量的原始值均源自时域信号,因此,只需将数据按一定频率导出即可.虽然导出时可以插值,以实现任意频率的样本,但是,采用与传感器相同的频率可以更真实的反应原始路面信息.最终以100 Hz频率导出4分钟的传感器信号作为辨识数据样本提供统计值的计算基础.
记实验中计算统计量所需的一段数据的长度为计算容量;记每次新增/丢弃的数据的长度为计算步长;记未更新数据的长度与计算窗口的比值为重复度.其两例计算方法如图4所示.第一组步长为100个值,数据总量也为100,即重复度为0;第二组步长为100个值,数据总量为300,即重复度为66.6%.

图4 数据结构示意图
辨识步长决定了路面辨识的实时频率,反比于辨识数据样本的频率即100 Hz;数据容量反映了统计特征的具体计算形式,同时,决定了辨识程序的开始时间,因此,不宜取得过大;在传感器采样频率及辨识步长一定的前提下,数据重复度体现了辨识时刻对过往行驶路面的考虑权重,即重复度就越大,所考虑的过往路面越长.
图5显示了步长为100的悬架动挠度均方根值计算结果,随着重复度增加,曲线细节略有丢失,曲线趋于平滑,但是,总体尖峰低谷位置不变幅值不变.
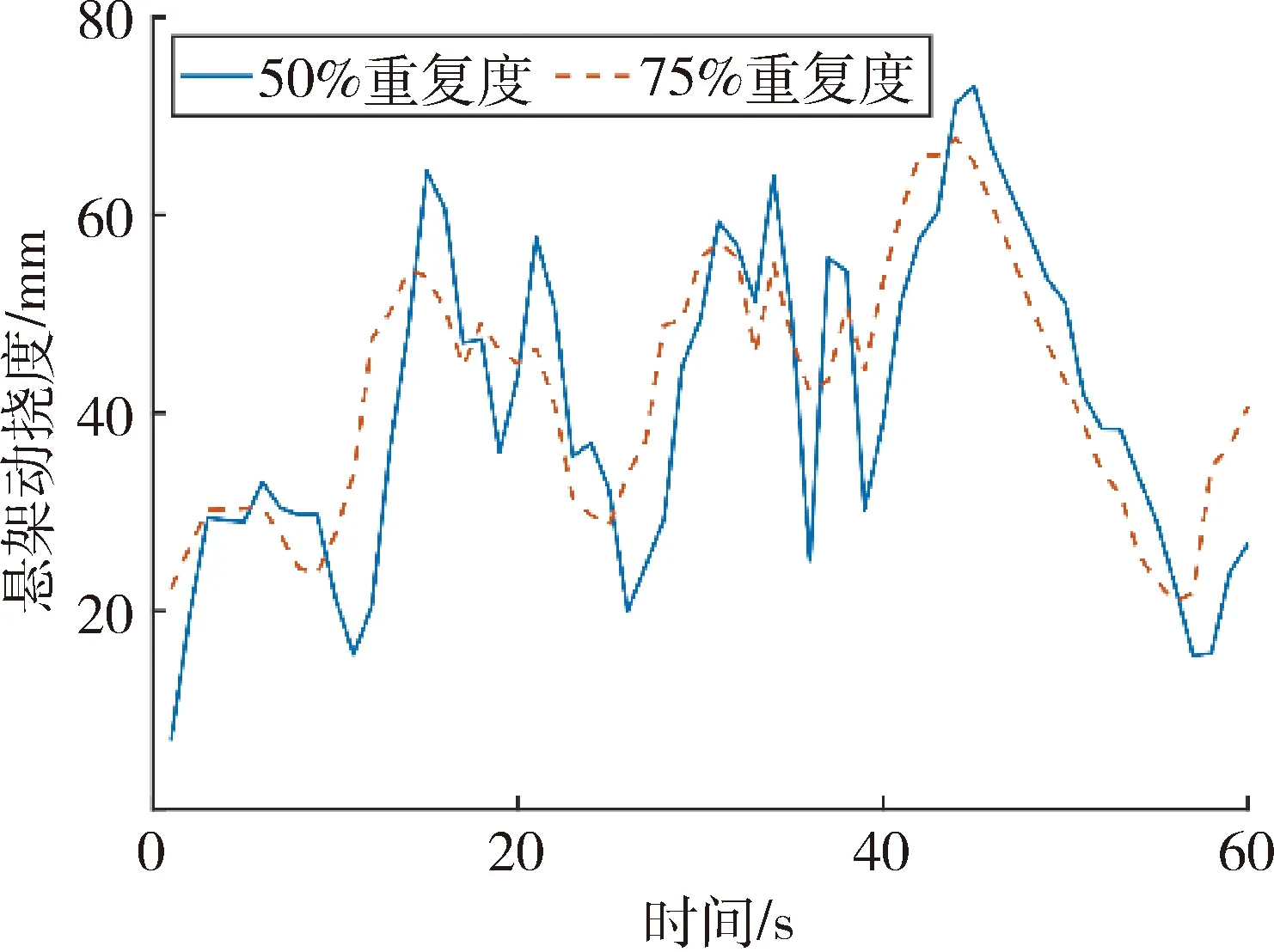
图5 均方根不同重复度对比
由于3个参量之间数量级差距较大,为防止收敛缓慢,需要进行归一化处理.
2.4 结果分析
(1)辨识方法对比分析
在采用相同的振动数据及其预处理方式的前提下,对比ELM及SVM方法在路面辨识精度及辨识速度之间的差异.
图6显示了两种不同学习模型的识别结果,二者精度相当,并且混淆情况相近,最好的辨识路面都为公路工况,但辨识速度差异较大.ELM属于传统人工神经网络的变种,核心参数依旧是直接输入与间接输入的权重,并通过简单求解方程即可得到最终模型,对于本次实验只有3个维度的数据,因此在英特尔i5-8265u,Windows10条件下的MATLAB运行中,ELM用时1.69秒,而且ELM模型可以与平台软件等解耦合,只需要获得核心矩阵就可以用在任何场合;SVM则需要自动训练一个合适的维度空间,并基于结构风险最小化原则生成此空间的分界线,需要频繁计算,因此,同平台用时137.41秒,显著慢于ELM.
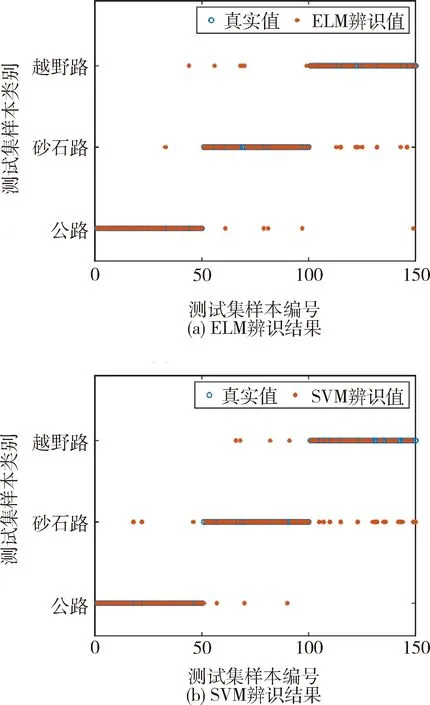
图6 学习模型辨识对比
(2)统计特征预处理方法对比分析
基于ELM方法,对比分析了数据预处理方法对辨识精度的影响规律.
图7显示了无重复度时,均方根值与峭度的辨识结果.采用均方根辨识的准确度为82%,并且主要错误集中在越野路和砂石路工况之间,分析原因为,砂石路与越野路工况下车辆振动有相似的高频反馈,增大了辨识机辨识错误的概率;使用峭度辨识时,无论何种路面都有严重的辨识错误问题,辨识准确度仅为50%.实验证明,相比于峭度方法,基于均方根处理的数据预处理方法,更适应于路面行驶工况辨识.
(3)计算不唱重读度对比分析
图8为3种不同计算步长与10种计算容量组成的30组实验结果对比图.结果表明,相同容量时,不同步长对辨识精度无明显有规律的影响;同一步长的情况下,辨识精度随容量的增加,也即重复度的增加而增加,并最终稳定在93%附近.
图9为步长100、容量500时的辨识结果,与图7(a)的步长100、容量100的辨识结果对比表明,增加重复度可显著改善砂石路与越野路之间辨识混淆情况,证明了重复度可以抑制砂石路高频小幅振动对辨识负面的影响.
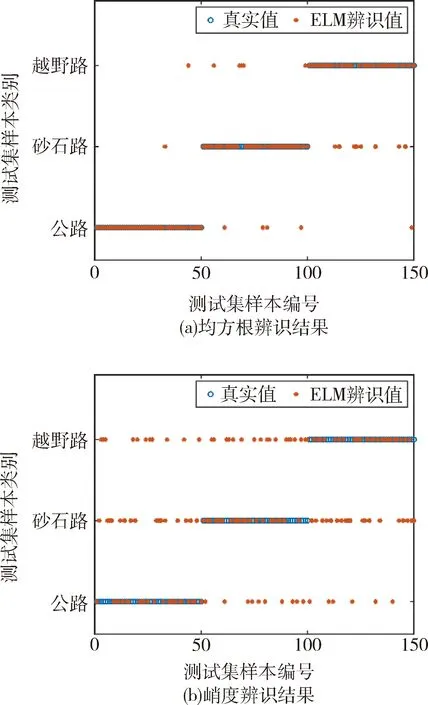
图7 统计特征辨识对比
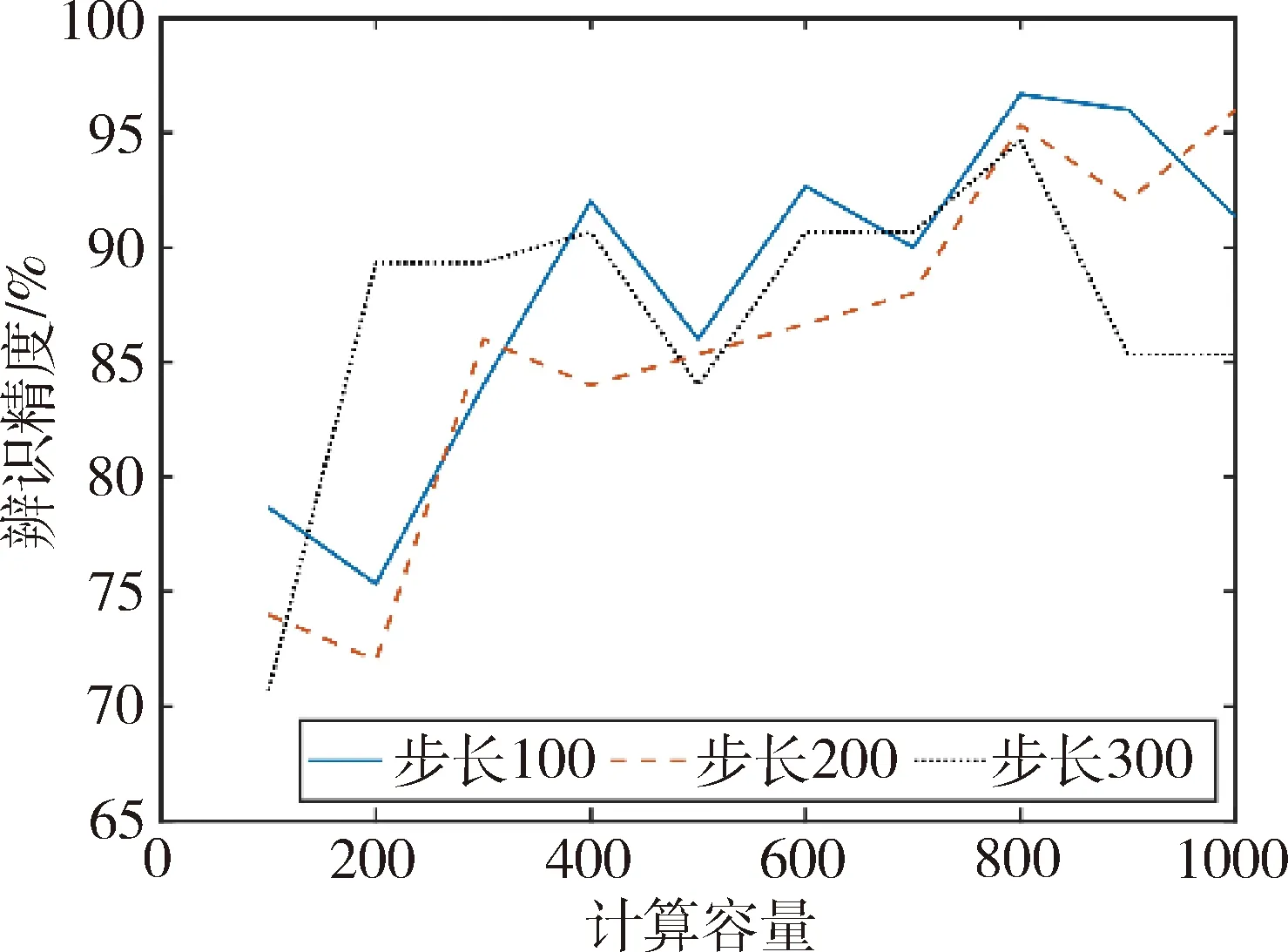
图8 不同步长与重复度对辨识精度影响
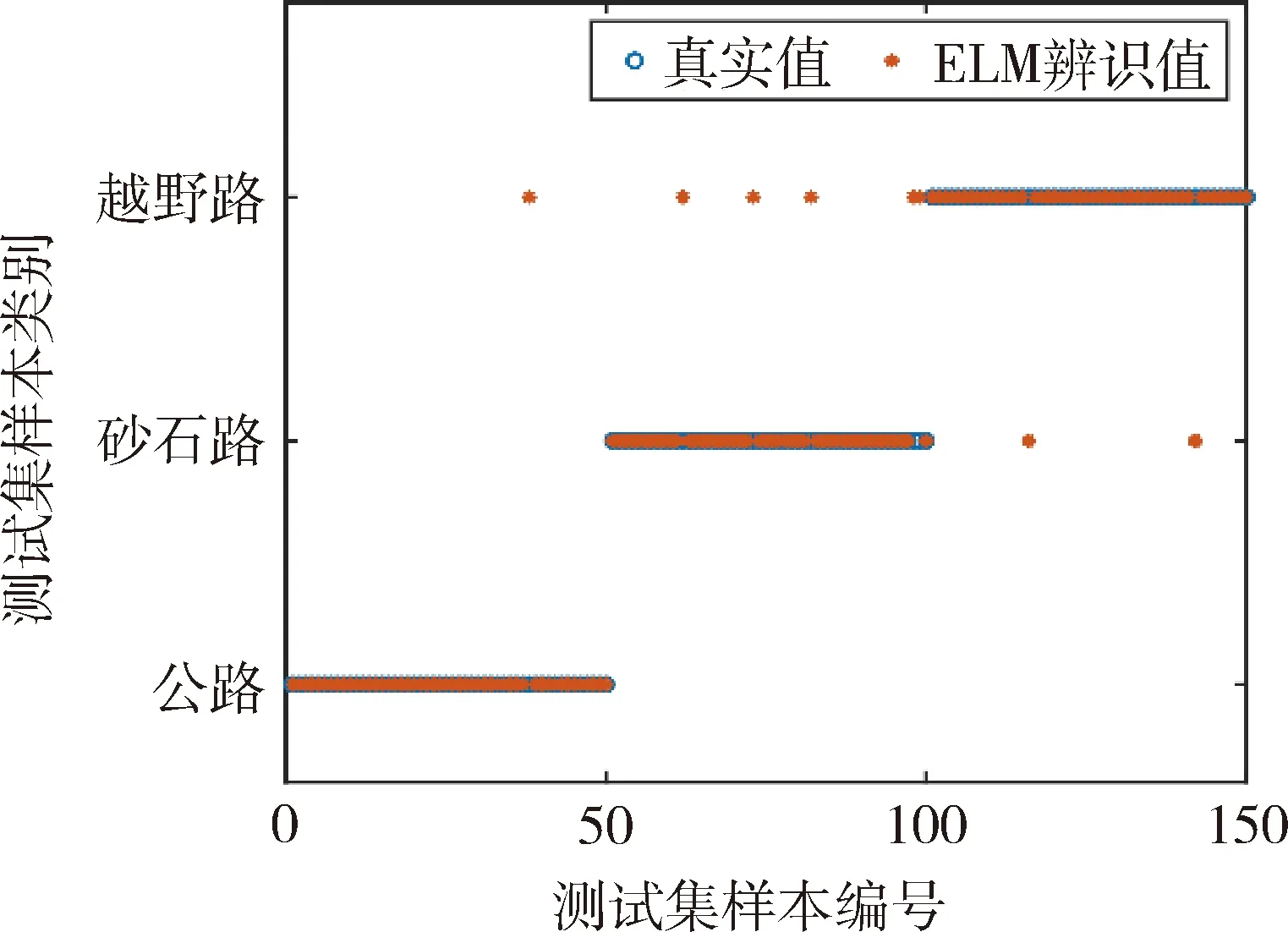
图9 步长100、容量500时的辨识结果
辨识步长对辨识准确度无明显影响,所以,可以适当增加步长以减少运算次数,但太大的步长会使辨识间隔增大,降低辨识实时性,因此需要根据实际需求设定辨识步长.
3 结 论
1)在数据维度不高时,ELM不仅可以获得与SVM相近的分类性能,且训练速度明显高于SVM.
2)车身振动响应数据信号可以用于行驶路面工况分类,能够取得良好的试验效果,能够弥补视觉或雷达技术易受环境条件影响的不足.
3)在原始振动数据预处理方面,使用40%~60%重复度的均方根值计算处理方式,可以在辨识精度和计算量之间取得较好的综合效果.
