An indirect approach for quantummechanical eigenproblems:duality transforms
2022-06-29YuJieChenShiLinLiWenDuLiandWuShengDai
Yu-Jie Chen,Shi-Lin Li,Wen-Du Li and Wu-Sheng Dai,*
1 Department of Physics,Tianjin University,Tianjin 300350,China
2 College of Physics and Materials Science,Tianjin Normal University,Tianjin 300387,China
Abstract We suggest an indirect approach for solving eigenproblems in quantum mechanics.Unlike the usual method,this method is not a technique for solving differential equations.There exists a duality among potentials in quantum mechanics.The first example is the Newton–Hooke duality revealed by Newton in Principia.Potentials that are dual to each other form a duality family consisting of infinite numbers of family members.If one potential in a duality family is solved,the solutions of all other potentials in the family can be obtained by duality transforms.Instead of directly solving the eigenequation of a given potential,we turn to solve one of its dual potentials which is easier to solve.The solution of the given potential can then be obtained from the solution of this dual potential by a duality transform.The approach is as follows:first to construct the duality family of the given potential,then to find a dual potential which is easier to solve in the family and solve it,and finally to obtain the solution of the given potential by the duality transform.In this paper,as examples,we solve exact solutions for general polynomial potentials.
Keywords:duality family,general polynomial potential,exact solution
1.Introduction
Eigenproblems are important in quantum mechanics and exact solutions are rare.In this paper,we seek exact solutions by a duality relation in mechanical systems.The first example of this duality is the Newton–Hooke duality in classical mechanics revealed by Newton inPrincipia(Corollary III of proposition VII)[1].The Newton–Hooke duality is a duality between the Newtonian gravitational potential and the Hookian harmonic-oscillator potential.E.Kasner and V.I.Arnold independently generalized the Newton–Hooke duality to general power potentials,called the Kasner–Arnold theorem[2–6].Recently,the duality between arbitrary potentials in quantum mechanics was reported[7].
In classical and quantum mechanics there exist duality families[7].In a duality family,potentials are related by a duality relation.Once a family member is solved,the solutions of all other family members can be obtained by a duality transform.That is,in a duality family,we in principle only need to solve one potential.This inspires us to develop an indirect approach for solving eigenproblems.
Suppose the eigenequation of the potentialVis difficult.According to the duality,the potentialVmust belong to a duality family which consists of an infinite number of potentials.All potentials inVʼs family are dual potentials ofV.If one potential inVʼs family is solved,the solution of the eigenequation ofVcan be obtained by the duality transform.
In the approach,the first step is to construct the duality family of the potentialVby the duality relation.The second step is to look for an‘easy’potential inVʼs family.The third step is to achieve the solution ofVby the duality transformation from the solution of the ‘easy’ potential.
The eigenproblem has been studied for a long time.Some exact solutions are obtained,such as the one- and threedimensional inverse square root potentials[8–11],the pseudo-Gaussian potential[12],the quasi-exactly solvable potential[13],and the Coulomb-type potential[14],and some methods are developed[15–19].However,due to the difficulty of seeking exact solutions,the research mainly focuses on solving isolated examples one by one.The method in this paper turns to finding exactly solvable families rather than directly solving a certain potential.

In section 2,we derive the duality relation for threedimensional polynomial central potentials.In section 3,we construct duality families.In sections 4–7,we give examples.In the appendices,we work out some exact solutions of‘easy’potentials.
2.Duality of general polynomial central potential
In this section,we consider the duality between general polynomial central potentials.The general polynomial is a polynomial with arbitrary real-number powers.Reference[7]gives a duality relation between arbitrary-dimensional central potentials:
The radial wave functions of the three-dimensional central potentialsU(r)andV(ρ)that satisfy the duality relation
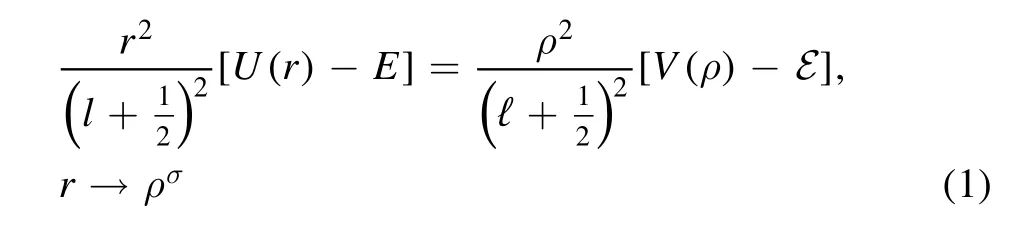
are related by the duality transform
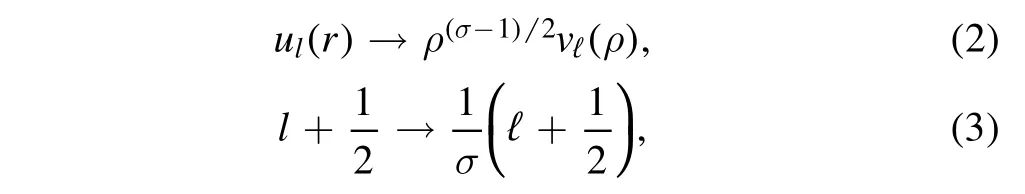
whereEandε are eigenvalues andland ℓ are angular quantum numbers.Here σ is an arbitrary constant.
Based on this duality relation,we derive the duality relation for the general polynomial central potential
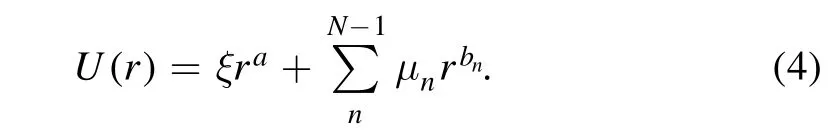
Here,for convenience,we deliberately arbitrarily write a term in the polynomial,say ξra,separately.
Substituting the general polynomial potential(4)into the duality relation(1)gives
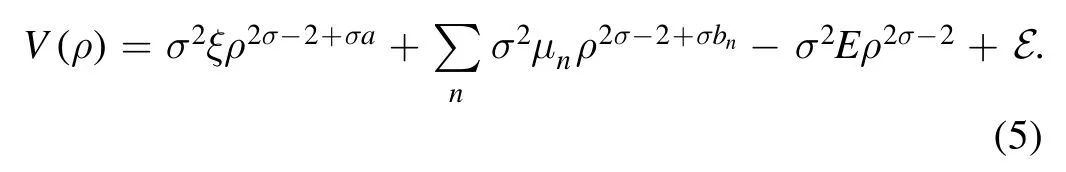
If requiring that the dual potential(5)is still anN-term general polynomial central potential,i.e.,
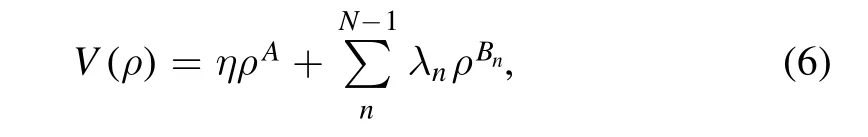
we haveNchoices.This means that anN-term general polynomial potential hasNdual general polynomial potentials.Without loss of generality,we choose
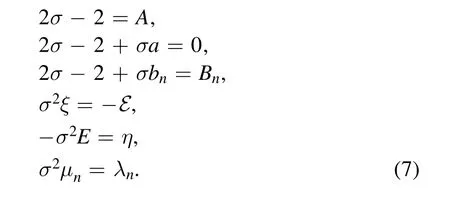
This gives
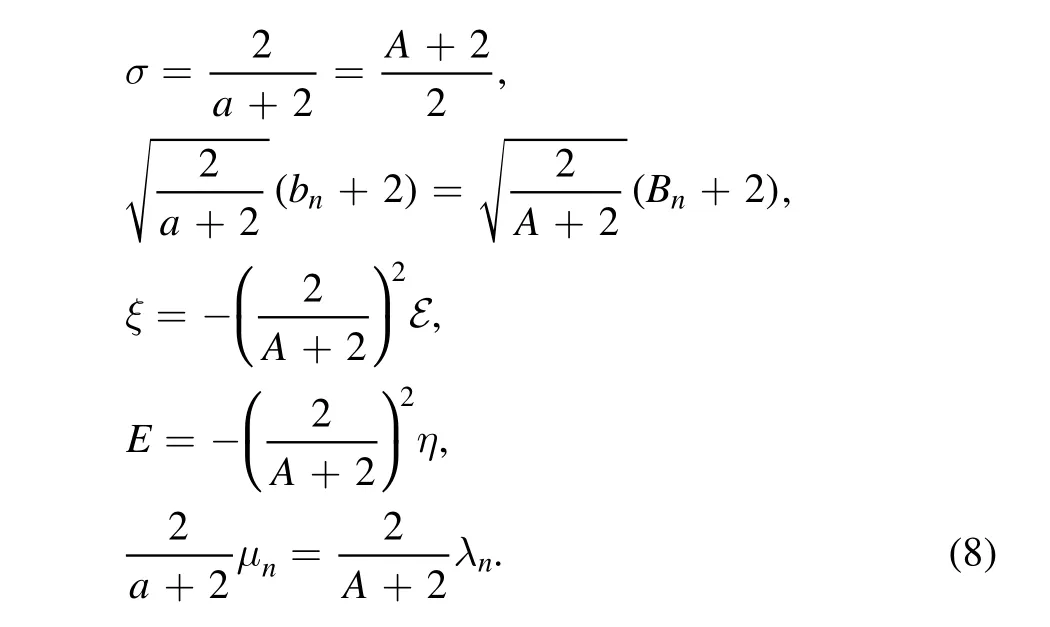
Then we arrive at the following conclusion.
Two general polynomial central potentials
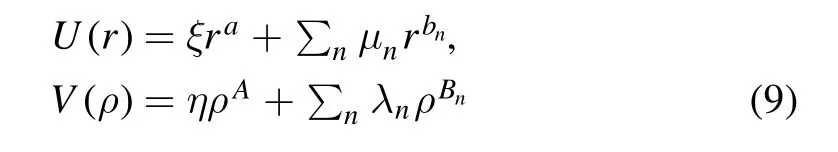
are dual to each other,if
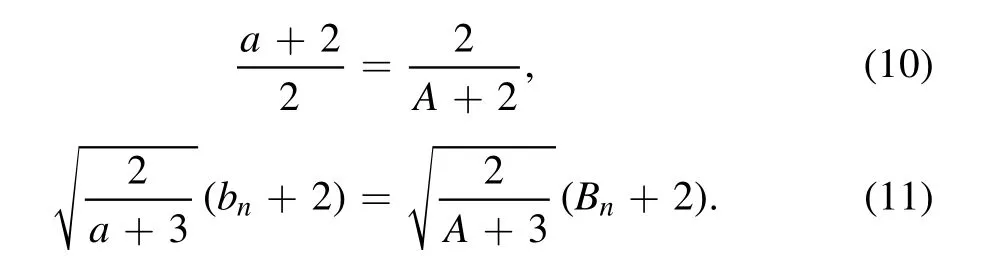
Their eigenfunctions are related by the duality transform

with

Their eigenvalues and their angular momenta are related by
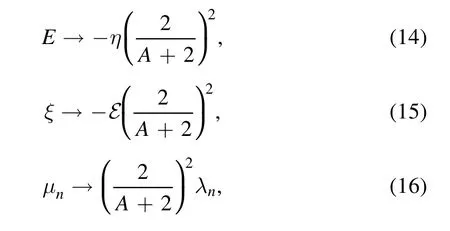
and
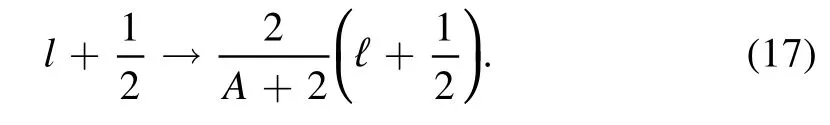
More concretely,substituting the duality relations(14)–(17)into the eigenvalue of the potentialU(r),
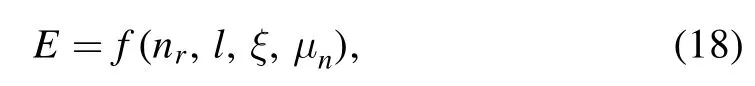
gives
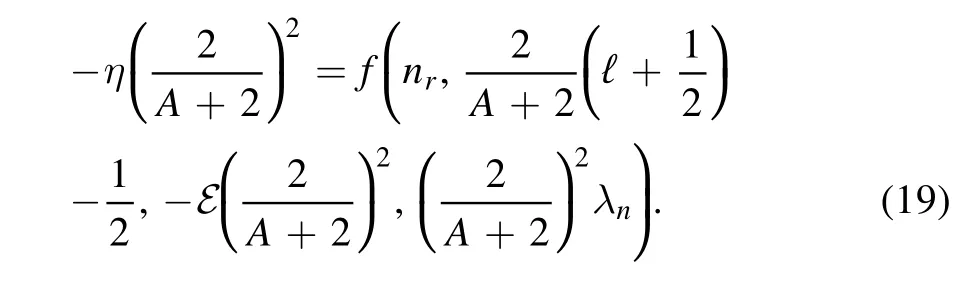
Then the eigenvalueε of the potentialV(ρ)reads
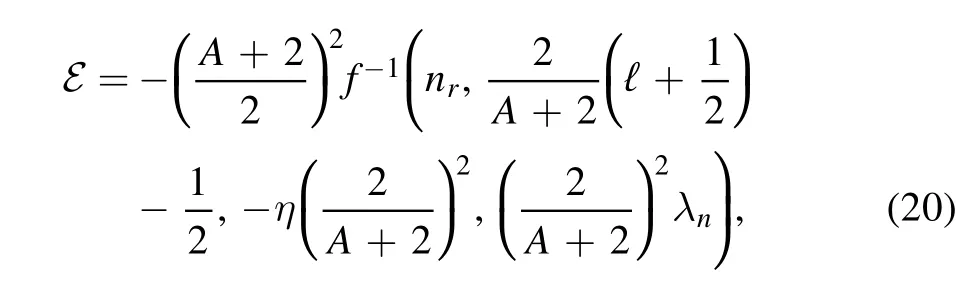
wheref−1denotes the inverse function off.
3.Solving an eigenproblem by constructing a duality family
All potentials that are dual to each other form a duality family.The family member is labeled by a parameter σ.In a duality family,once a potential is solved,the solutions of all other potentials in the family can be obtained by a duality transform.This inspires the idea that if a potential is difficult to solve,we may first construct its duality family and then see if there are any potentials in the family that are easy to solve.If there is a family member that can be solved,then the potential we want to solve can be solved by the duality transform.This approach requires that we must find a solved potential in the duality family.
Note that not all dual potentials of a physical potential are physical potentials.Some dual potentials of a physical potential are unphysical lower-unbounded potentials.These unphysical potentials still make sense in solving eigenvalue problems.A bound-state solution after a duality transform is still a bound-state solution.If a potential has only bound states,but its dual potential has scattering states,the scattering-state solution can be obtained by the duality transform from the scattering-state solution of its unphysical lowerunbounded dual potential.
A duality family consists of infinite family members.However,anN-term polynomial potential only hasNdualNterm polynomial potentials.
In the following,we solve some general polynomial potentials by virtue of the duality transform.
3.1.Two-term polynomial central potential
As an example,consider the two-term polynomial central potential
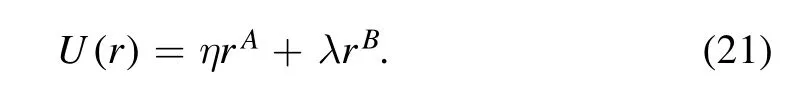
The general form of a family member in a duality family by the duality relation(1)is
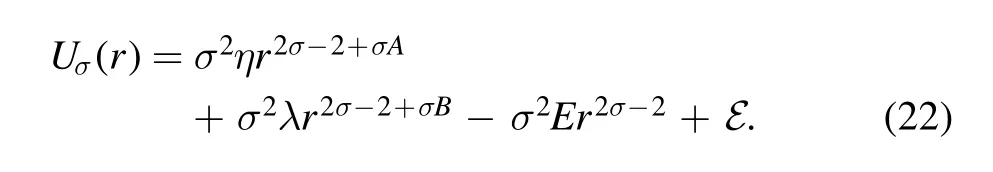
The family member is labeled by the parameter σ.
There is an infinite number of family members in a duality family;here we only focus on a special case:two-term polynomial potentials.
If requiring the dual potential of a two-term polynomial potential is still a two-term polynomial potential,there are only three choices of the parameter σ:σ=1,,and.
For σ=1,
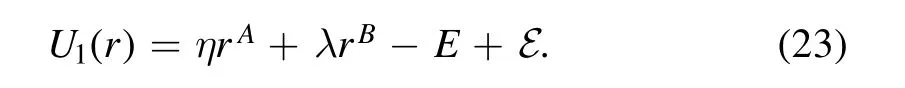
The requirement that the dual potential has only two terms requires that

i.e.,
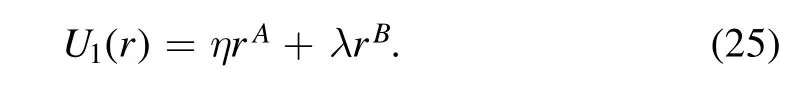
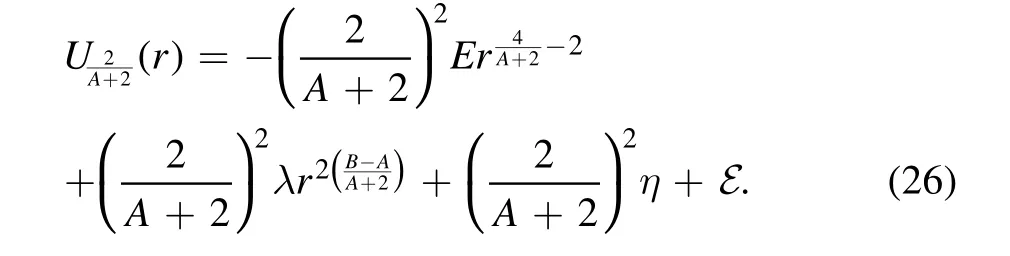
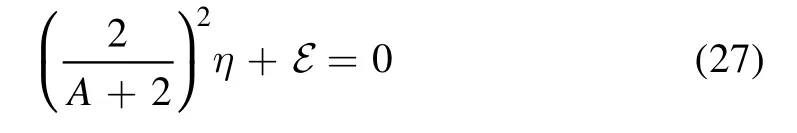
and we have
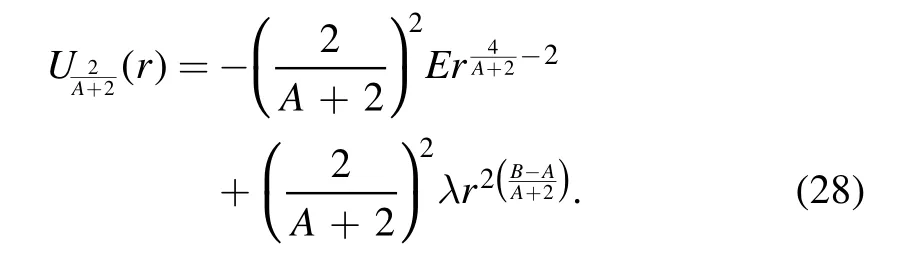
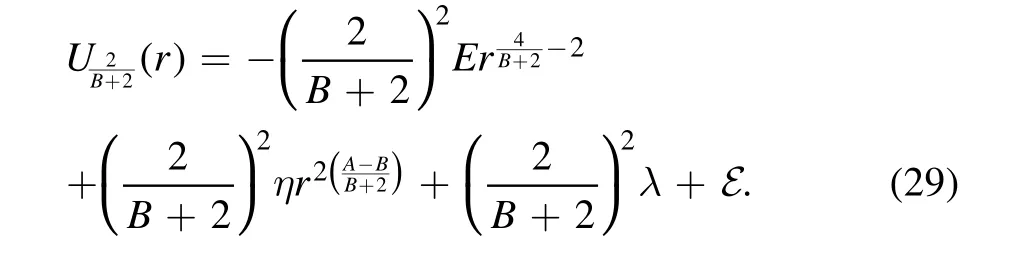
Similarly,choosing

gives
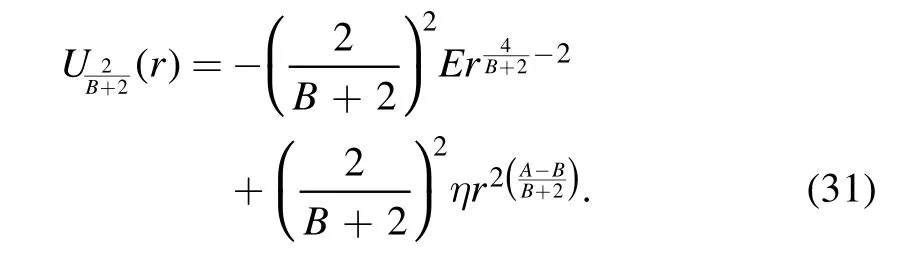
The duality family of two-term general polynomial central potentials consists of the following three family members:
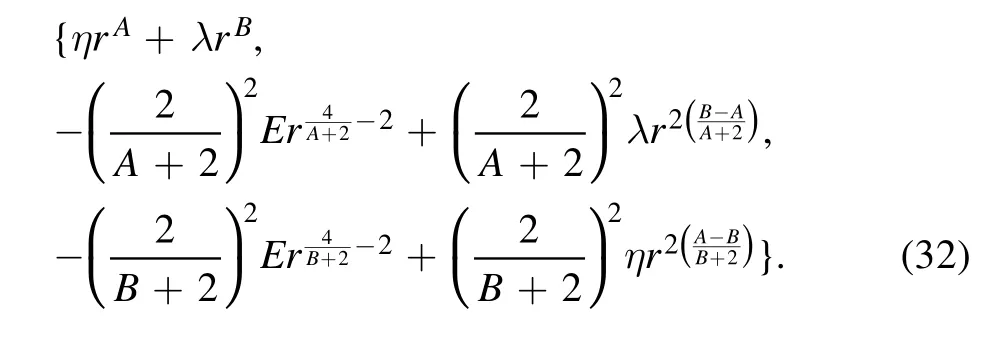
3.2.Three-term polynomial central potential
Similarly,we consider the three-term polynomial central potential
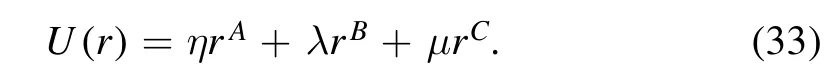
The family member is of the form
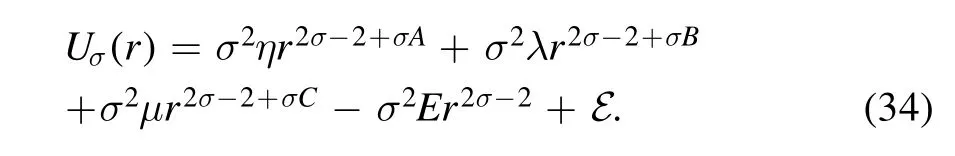
If requiring the dual potential of a three-term polynomial potential is still a three-term polynomial potential,there are only four choices:σ=1,.
In the bustle9 and hurry of departure, the cunning fisherman contrived10 that their boat should be the last to put off, and when everything was ready, and the sails about to be set, he suddenly called out: Oh, dear, what shall I do! I have left my best knife behind in the hut
For σ=1,
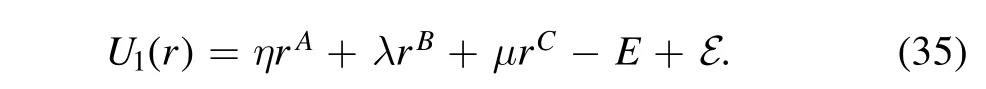
Choosing

gives a three-term polynomial potential,
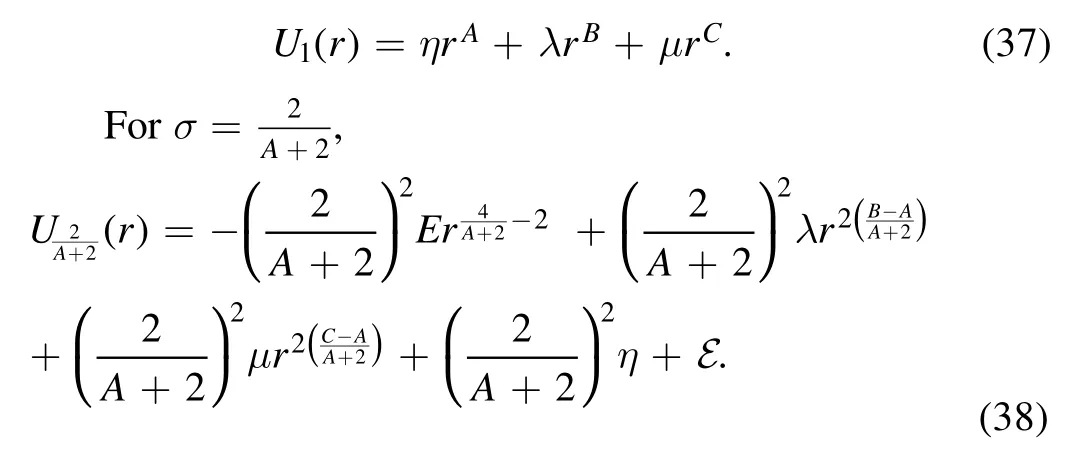
Choosing
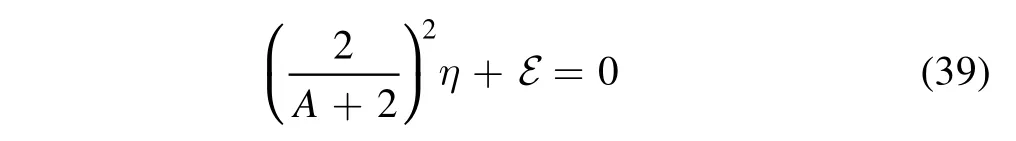
gives
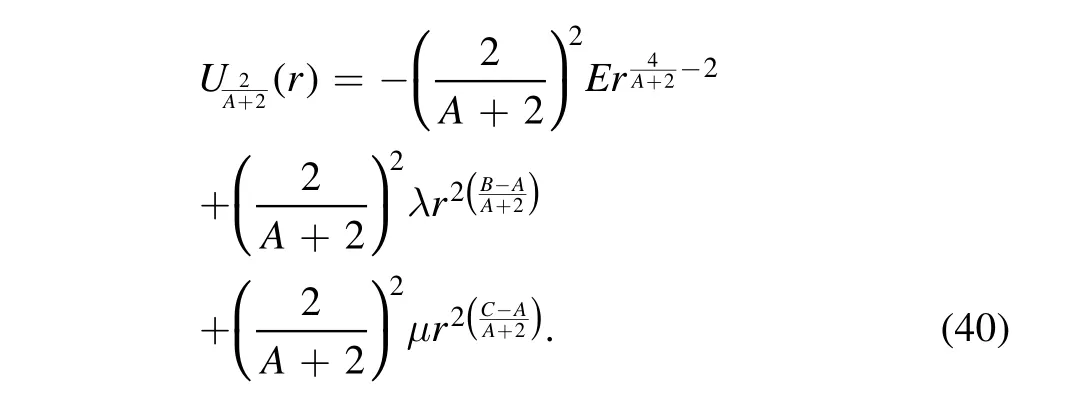

Choosing
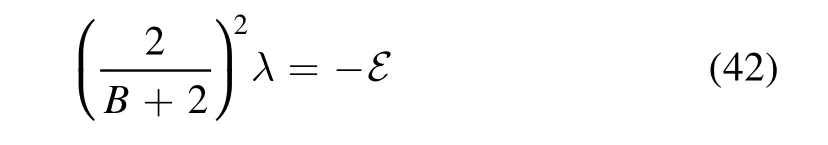
gives
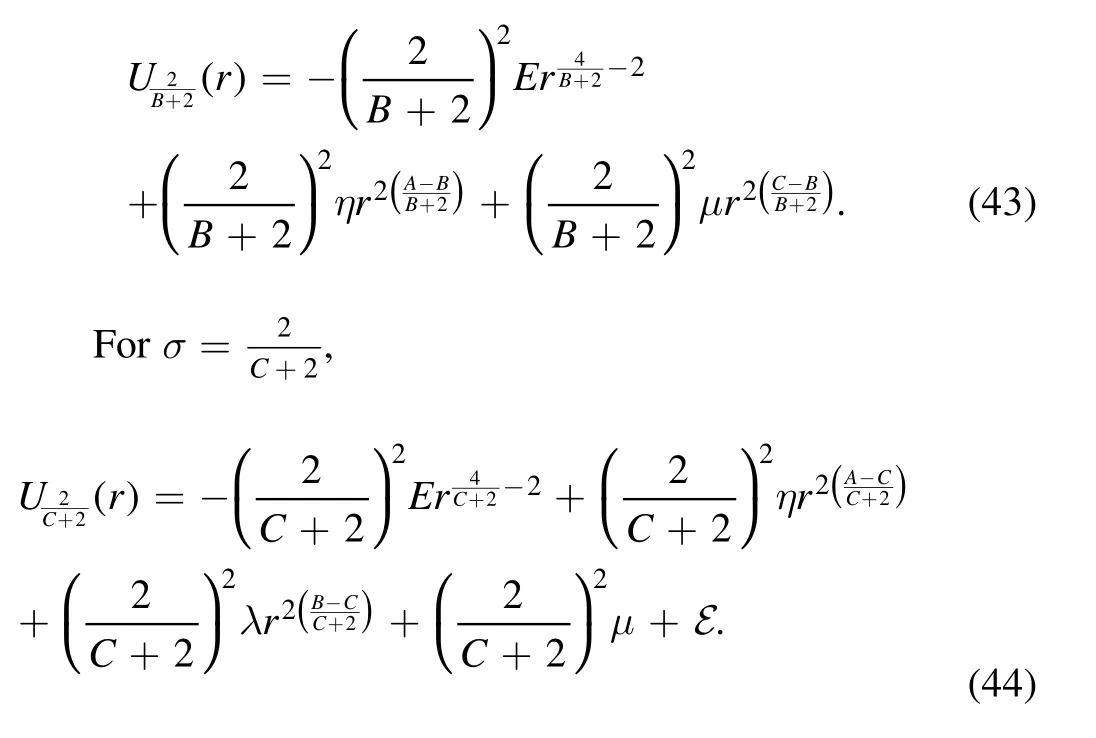
Choosing
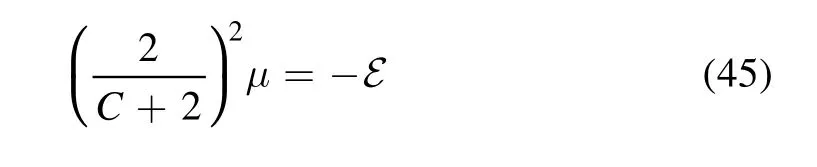
gives
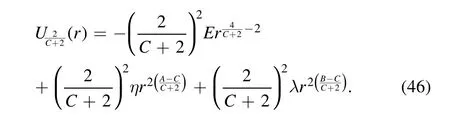
The duality family of three-term general polynomial central potentials consists of four family members:
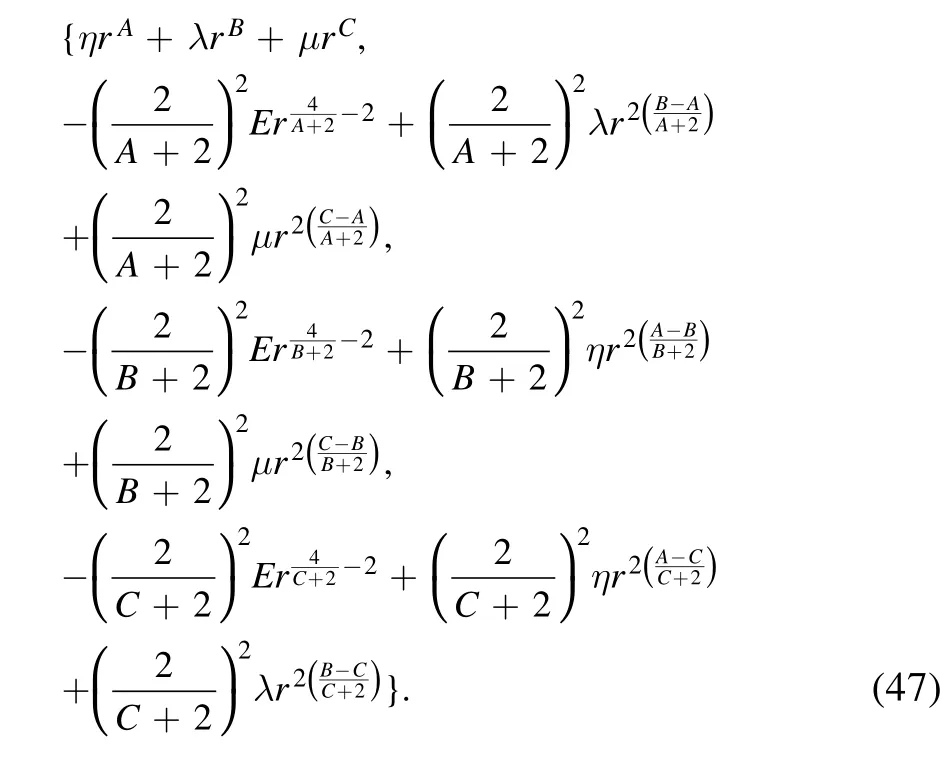
4.Solving and ηr2+λr6 from



4.1.


4.2.V(ρ)=ηρ2+λρ6

5.Solving andfrom ξr2+μr

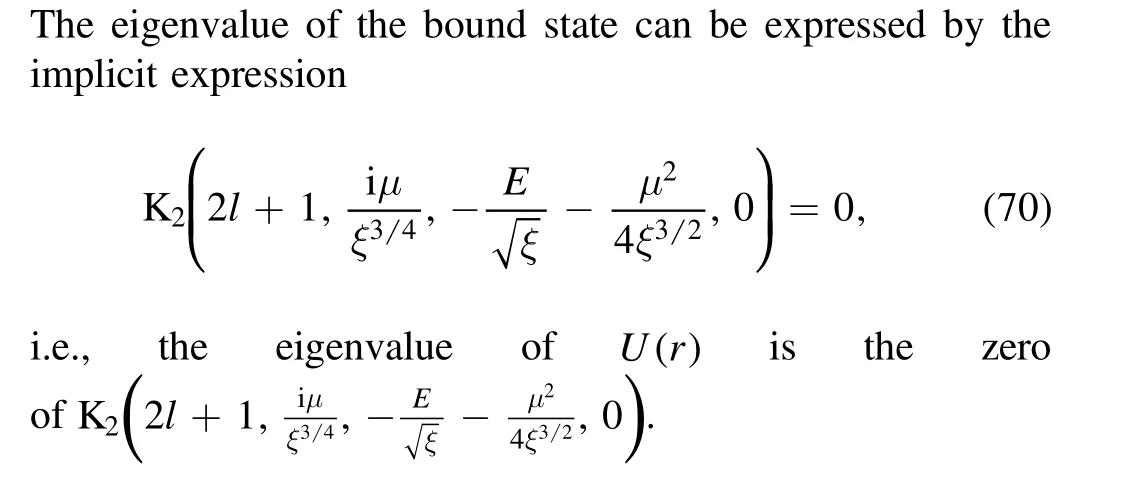
5.1.


5.2.
The potential(66)is another dual potential of the potential(67)witha=1,b=2 andA=−2/3,B=2/3 in the duality relations(10)and(11).

6.Solving and ηr6+λr4 from


6.1.


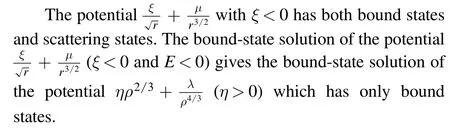
6.2.V(ρ)=ηρ6+λρ4


7.Solving ,andfrom
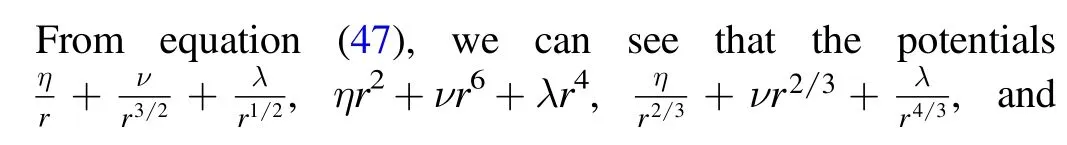

7.1.


7.2.V(ρ)=ηρ2+νρ6+λρ4


7.3.

8.Conclusion
We suggest a method for solving eigenproblems in quantum mechanics.This is an indirect method.Unlike the usual method,this method is not a technique of solving differential equations.The example given by Newton himself demonstrates how to obtain the solution of the harmonic oscillator potential from the solution of the Newtonian gravitational potential,or vice versa.
The key of the method is to first construct the dual family of the potential to be solved,and then to look for the solvable member in the duality family.If there is a solvable member,all family members,including the potential we want,can be solved by the duality transform.
It is not only the Schrödinger equation that has such a kind of duality.This duality also exists in,e.g.,the scalar field equation[7]and the Gross–Pitaevskii equation[23].The duality can also be applied to long-range potential scattering[24].The duality relation can be further used to solve other equations.For example,in gravity problems,we also need to solve eigenproblems in curved space[25–27].This method can also be used to seek the exact solutions of eigenproblems in curved space.
It is worth noting that the exact solutions obtained in this paper contain some long-range potentials.For short-range potentials which have only scattering states,there is a uniform treatment since for short-range potentials the scattering boundary conditions are the same[22,28–30].Long-range potentials may have both scattering and bound states or only bound states.For long-range potential scattering,the scattering boundary conditions depend on potentials and different potentials have different scattering boundary conditions[31–37].Exact solutions play an important role in long-range potential scattering.The exact solution obtained in the paper can also be used to study bound states,e.g.,the existence of bound states[38,39]and the number of bound states[40–42,42,43].
Acknowledgments
We are very indebted to Dr G Zeitrauman for his encouragement.This work is supported in part by the Special Funds for Theoretical Physics Research Program of the NSFC under Grant No.11947124,and NSFC under Grant Nos.11575125 and 11675119.
Appendix A.The exact solution of
In this appendix,we provide an exact solution of the eigenproblem of the potential
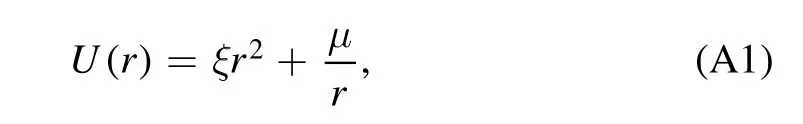
by solving the radial equation directly.This potential has only bound states.
The radial equation of the potential(A1)reads

Using the variable substitution

and introducingfl(z)by
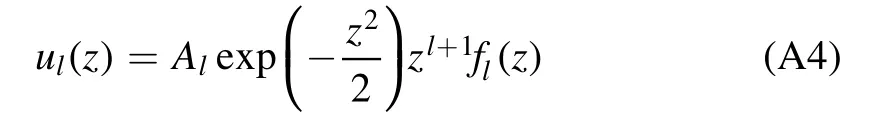
withAla constant,we convert the radial equation(A2)into an equation offl(z):
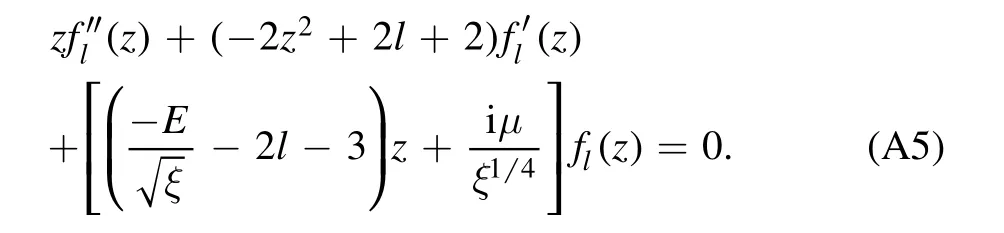
This is a biconfluent Heun equation[20].
The choice of the boundary condition has been discussed in[9].
A.1.The regular solution
The regular solution is a solution satisfying the boundary condition atr=0[9].The regular solution atr=0 should satisfy the boundary condition.In this section,we provide the regular solution of equation(A5).
The biconfluent Heun equation(A5)has two linearly independent solutions[20],
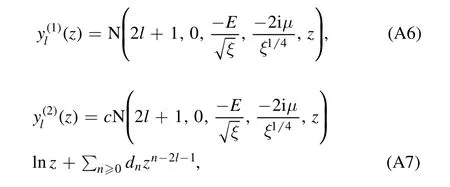
where
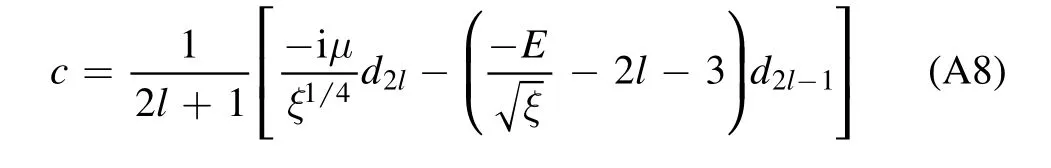
is a constant with the coefficientdνgiven by the following recurrence relation:
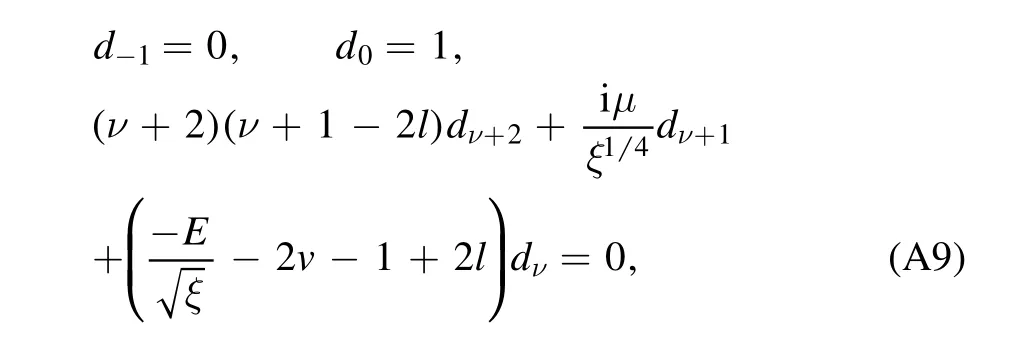
and N(α,β,γ,δ,z)is the biconfluent Heun function[9,20,21].


A.2.The irregular solution
The irregular solution is a solution satisfying the boundary condition atr→∞[9].
The biconfluent Heun equation(A5)has two linearly independent irregular solutions[20]:
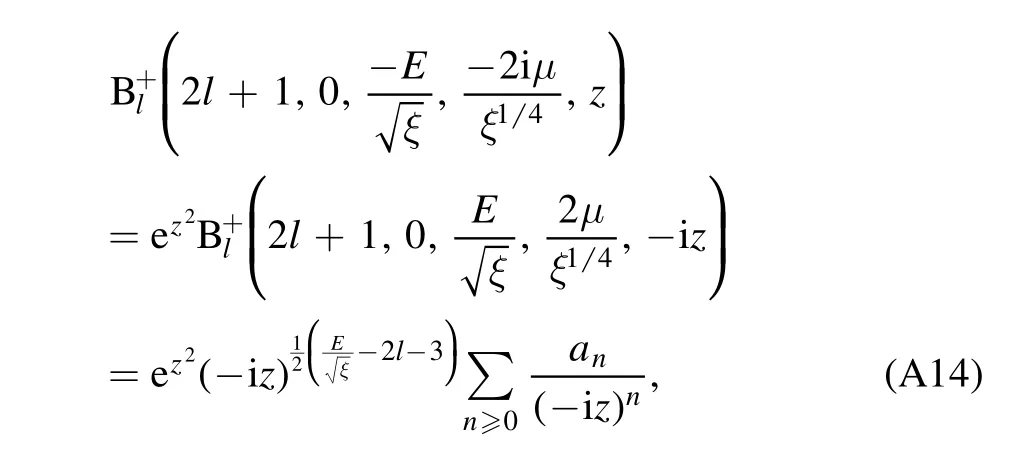
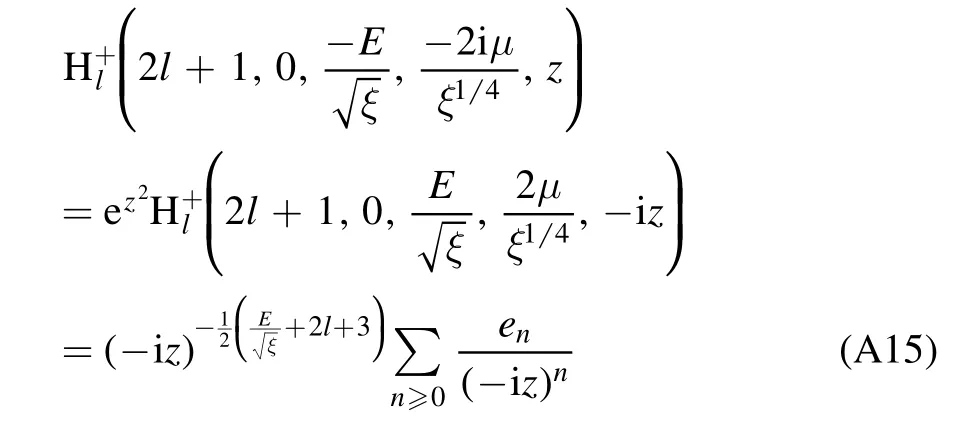
with the expansion coefficients given by the recurrence relation

and

A.3.Eigenfunctions and eigenvalues
To construct the solution,we first express the regular solution(A13)as a linear combination of the two irregular solutions(A14)and(A15).
The regular solution(A13),with the relation[9,20]

and the expansions(A14)and(A15),becomes

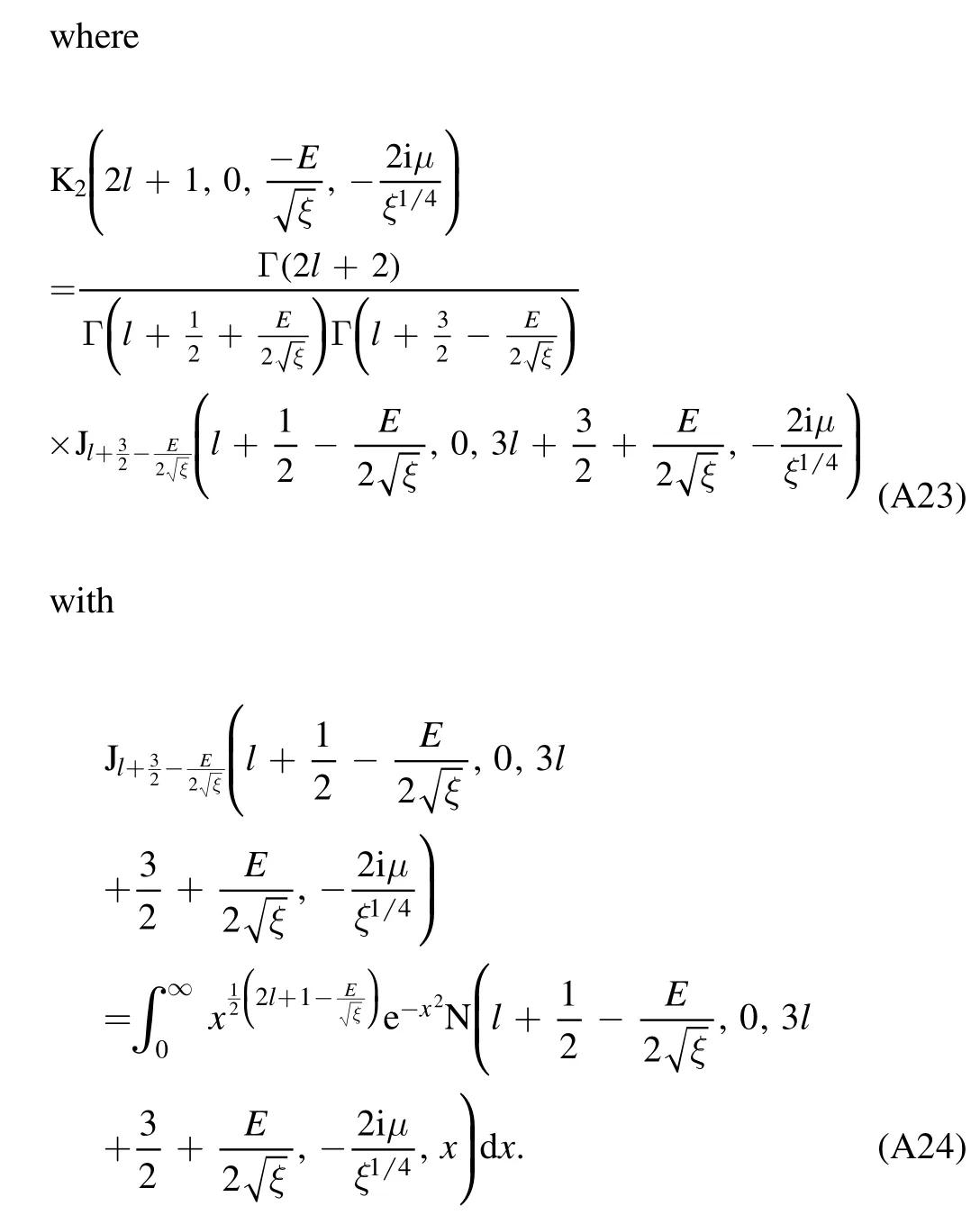
Equation(A22)is an implicit expression of the eigenvalue.
The eigenfunction,from equations(A21)and(A22),reads
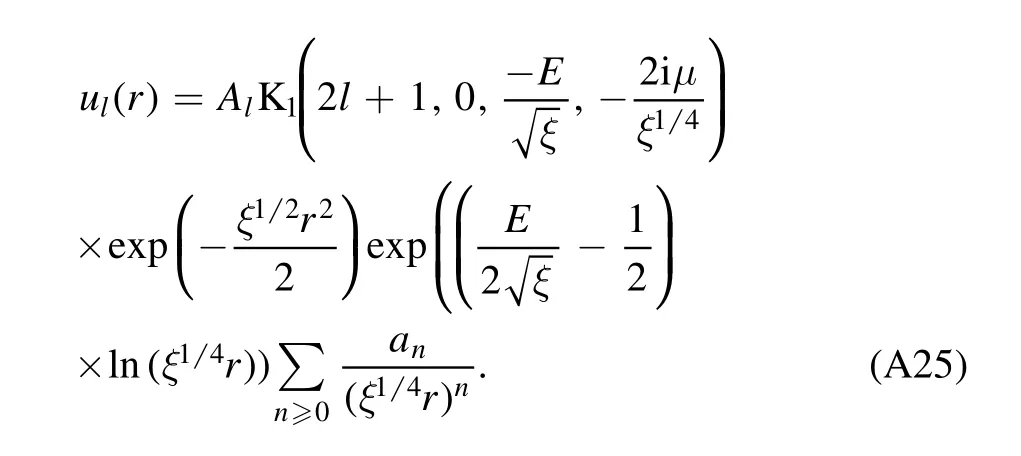
Appendix B.The exact solution of U(r)=ξr2+μr
In this appendix,we provide an exact solution of the eigenproblem of the potential

by solving the radial equation directly.This potential has only bound states.
The radial equation reads
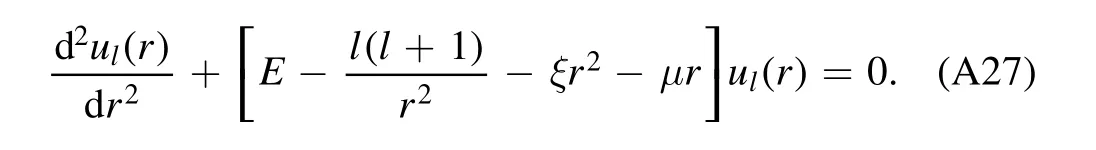
Using the variable substitution

and introducingfl(z)by
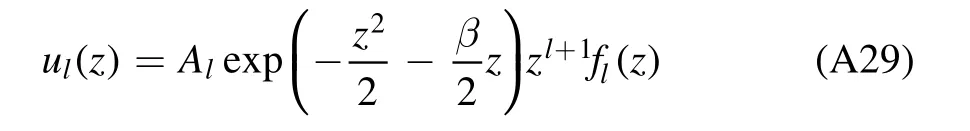
withAla constant,we convert the radial equation(A27)into an equation offl(z):

This is a biconfluent Heun equation[20].
The choice of the boundary condition has been discussed in[9].
B.1.The regular solution
The regular solution is a solution satisfying the boundary condition atr=0[9].The regular solution atr=0 should satisfy the boundary condition.In this section,we provide the regular solution of equation(A30).
The biconfluent Heun equation(A30)has two linearly independent solutions[20]:
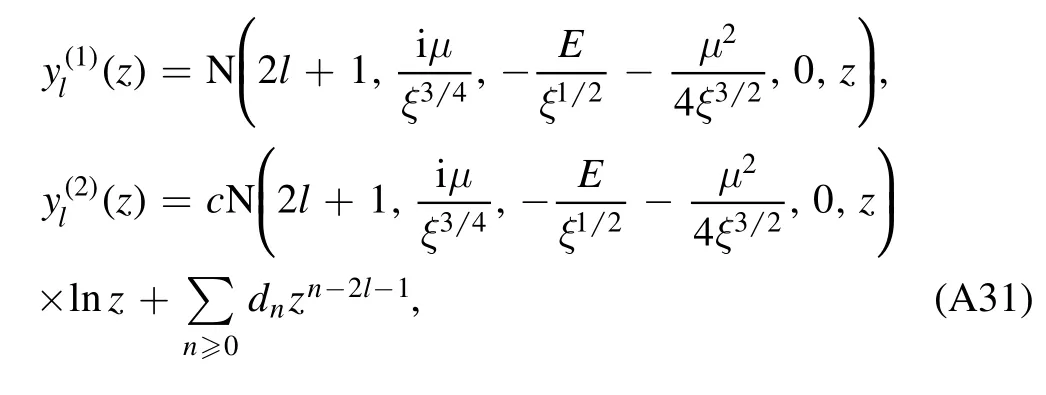
where

is a constant with the coefficientdνgiven by the following recurrence relation:

where the expansion coefficients are determined by the recurrence relation


B.2.The irregular solution
The irregular solution is a solution satisfying the boundary condition atr→∞[9].
The biconfluent Heun equation(A30)has two linearly independent irregular solutions[20]:
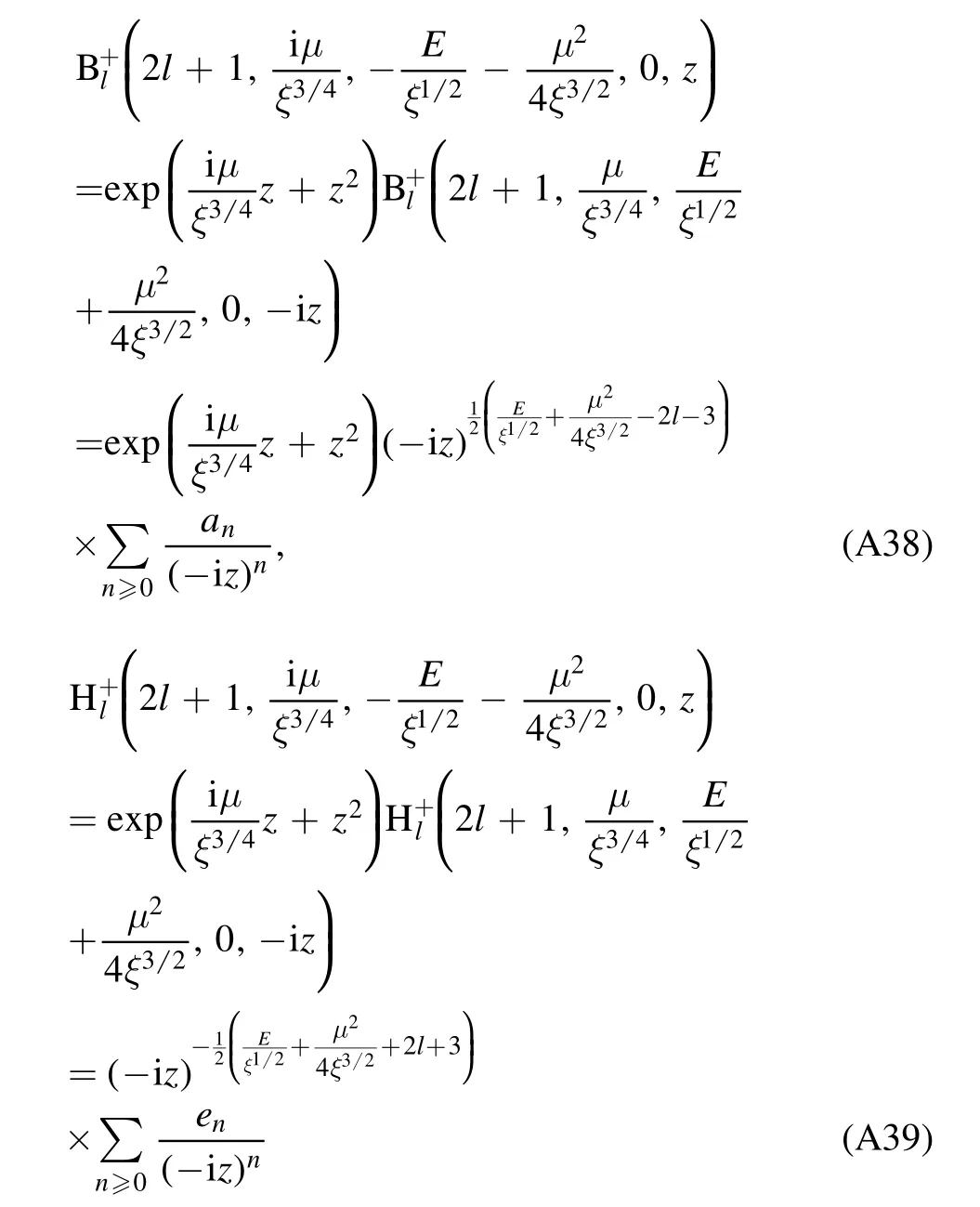
with the expansion coefficients given by the recurrence relation
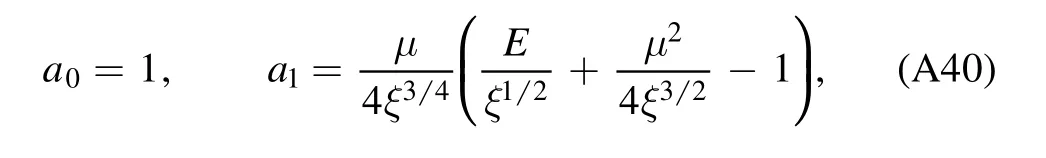
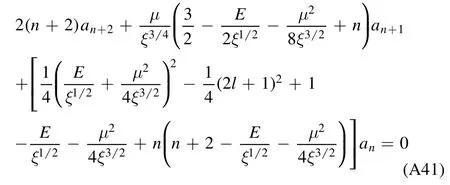
and

B.3.Eigenfunctions and eigenvalues
To construct the solution,we first express the regular solution(A37)as a linear combination of the two irregular solutions(A38)and(A39).
The regular solution(A37),with the relation[9,20]
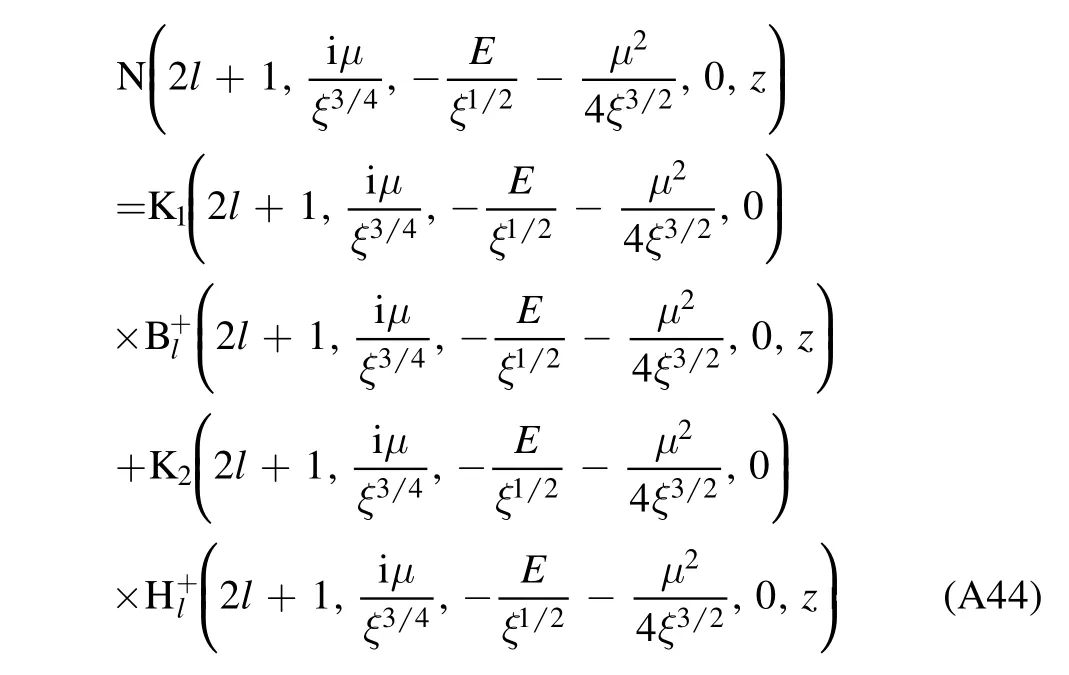
and the expansions(A38)and(A39),becomes
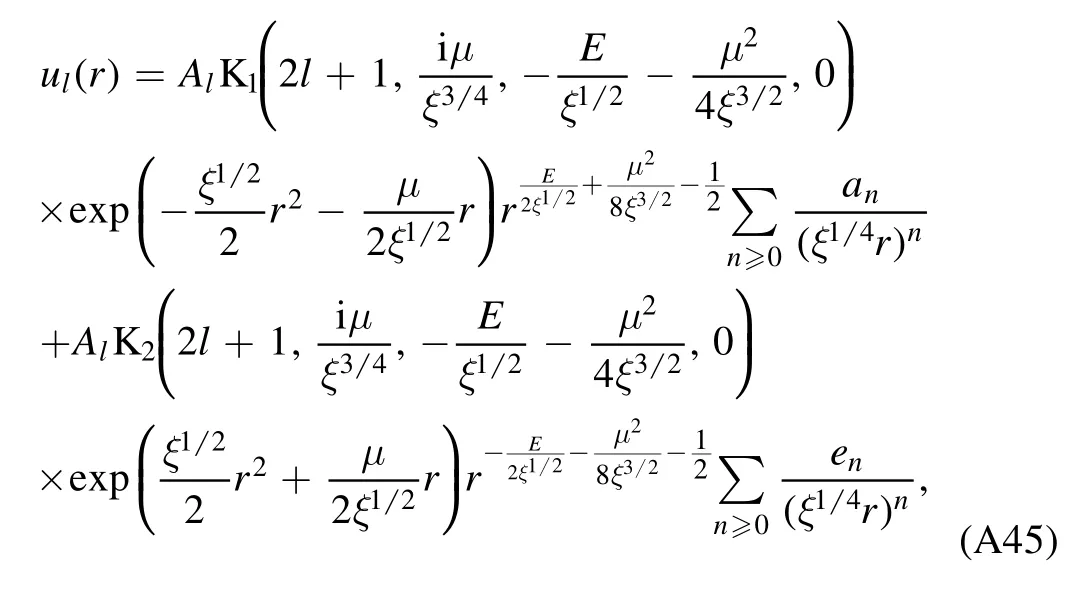


Appendix C.The exact solution of
In this appendix,we provide an exact solution of the eigenproblem of the potential

by solving the radial equation directly.This potential has both bound states and scattering states.
The radial equation reads
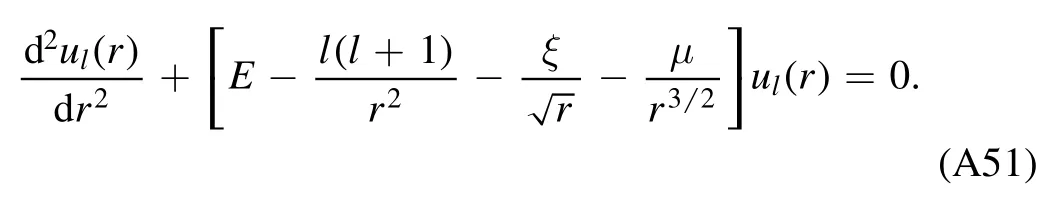
Using the variable substitution

and introducingfl(z)by
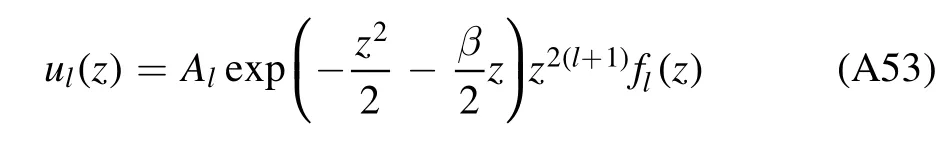
withAla constant,we convert the radial equation(A51)into an equation offl(z):
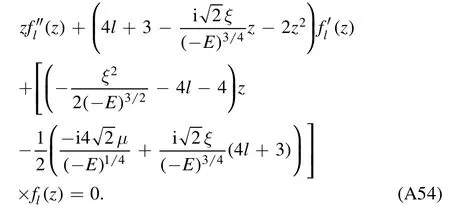
This is a biconfluent Heun equation[20].
The choice of the boundary condition has been discussed in[9].
C.1.The regular solution

where
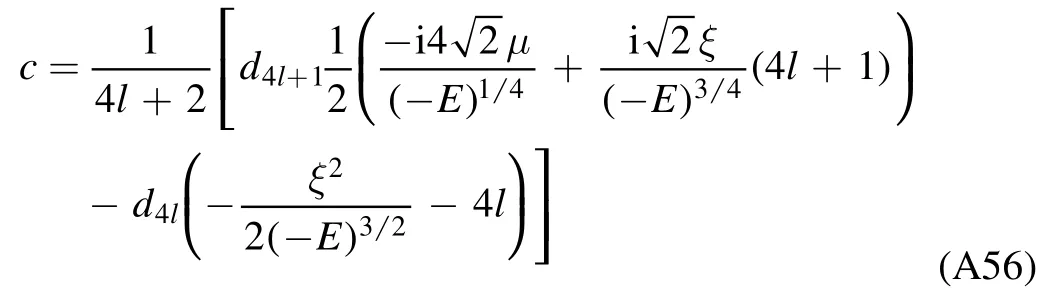
is a constant with the coefficientdνgiven by the following recurrence relation:
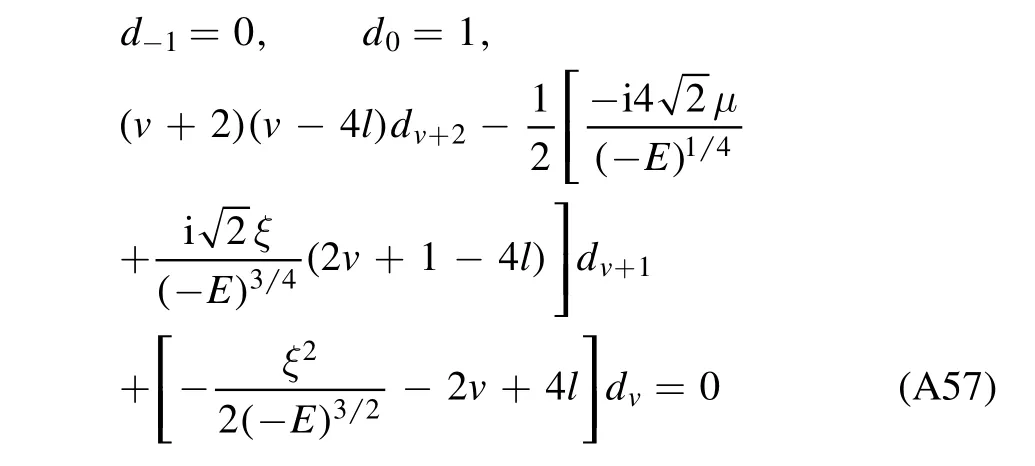
and N(α,β,γ,δ,z)is the biconfluent Heun function[9,20,21].

where the expansion coefficients are determined by the recurrence relation

From equation(A3),we obtain the regular solution

C.2.Irregular solution
The irregular solution is a solution satisfying the boundary condition atr→∞[9].The boundary conditions for bound states and scattering states atr→∞are different.
The biconfluent Heun equation(A54)has two linearly independent irregular solutions[20]:

with the expansion coefficients given by the recurrence relation
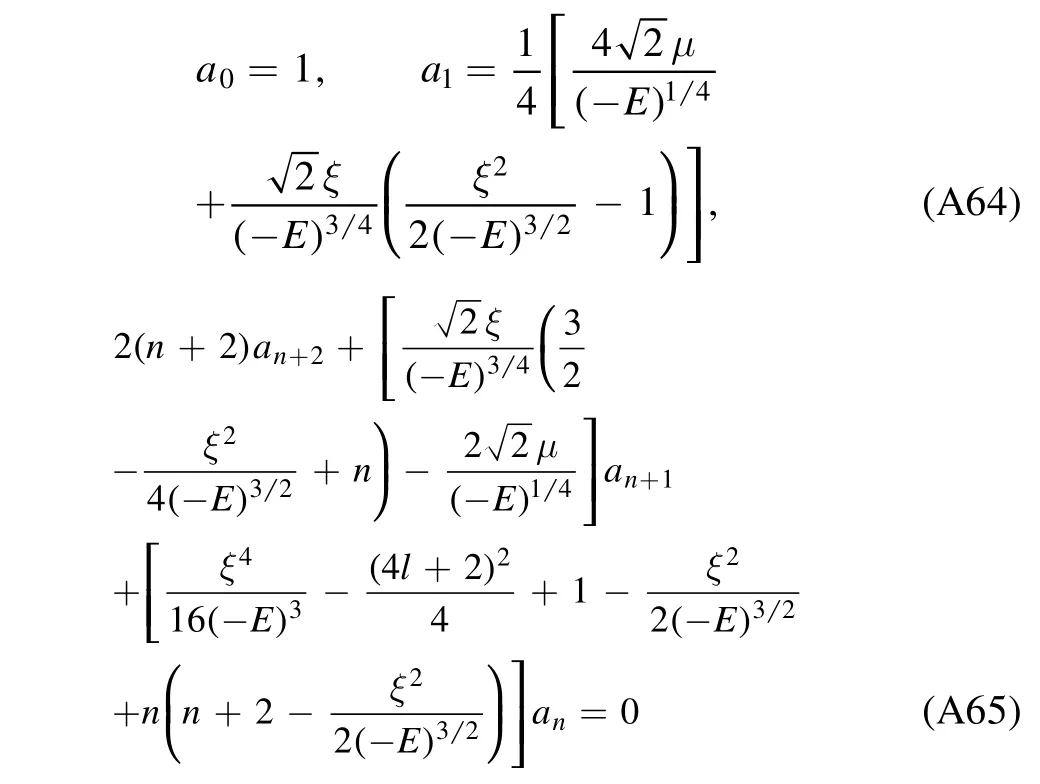
and
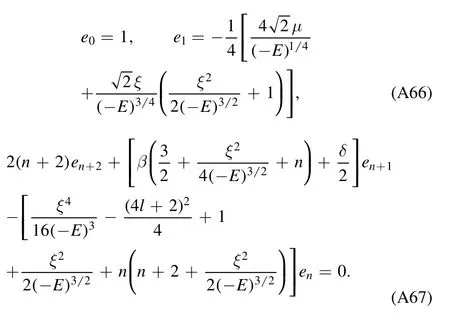
C.3.Bound states and scattering states
C.3.1.The bound state
To construct the solution,we first express the regular solution(A61)as a linear combination of the two irregular solutions(A62)and(A63).
The regular solution(A61),with the relation[9,20]

and the expansions(A62)and(A63),become
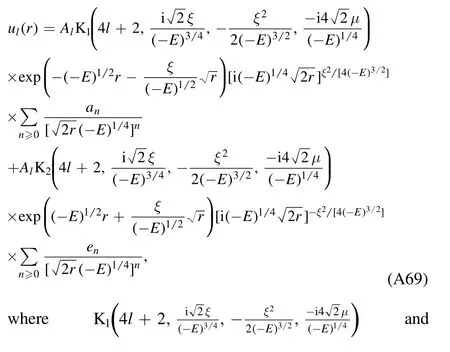


C.3.2.The scattering state



Appendix D.The exact solution of
In this appendix,we provide an exact solution of the eigenproblem of the potential

by solving the radial equation directly.This potential has only bound states.
The radial equation reads
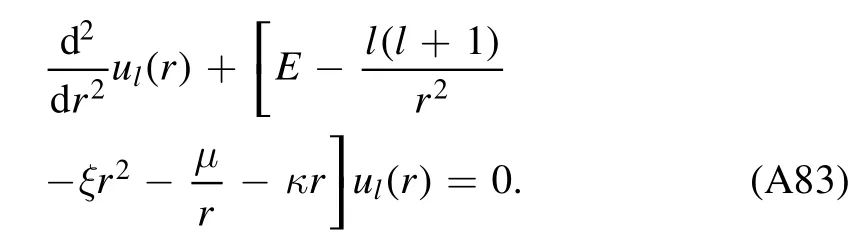
Using the variable substitution

and introducingfl(z)by
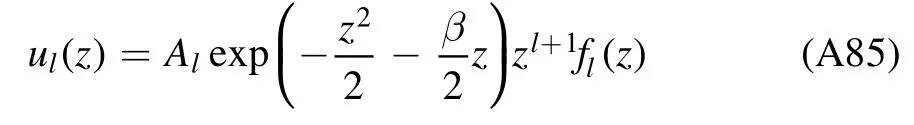
withAla constant,we convert the radial equation(A83)into an equation offl(z):

This is a biconfluent Heun equation[20].
The choice of the boundary condition has been discussed in[9].
D.1.The regular solution



D.2.The irregular solution
The irregular solution is a solution satisfying the boundary condition atr→∞[9].
The biconfluent Heun equation(A86)has two linearly independent irregular solutions[20]:

with the expansion coefficients given by the recurrence relation
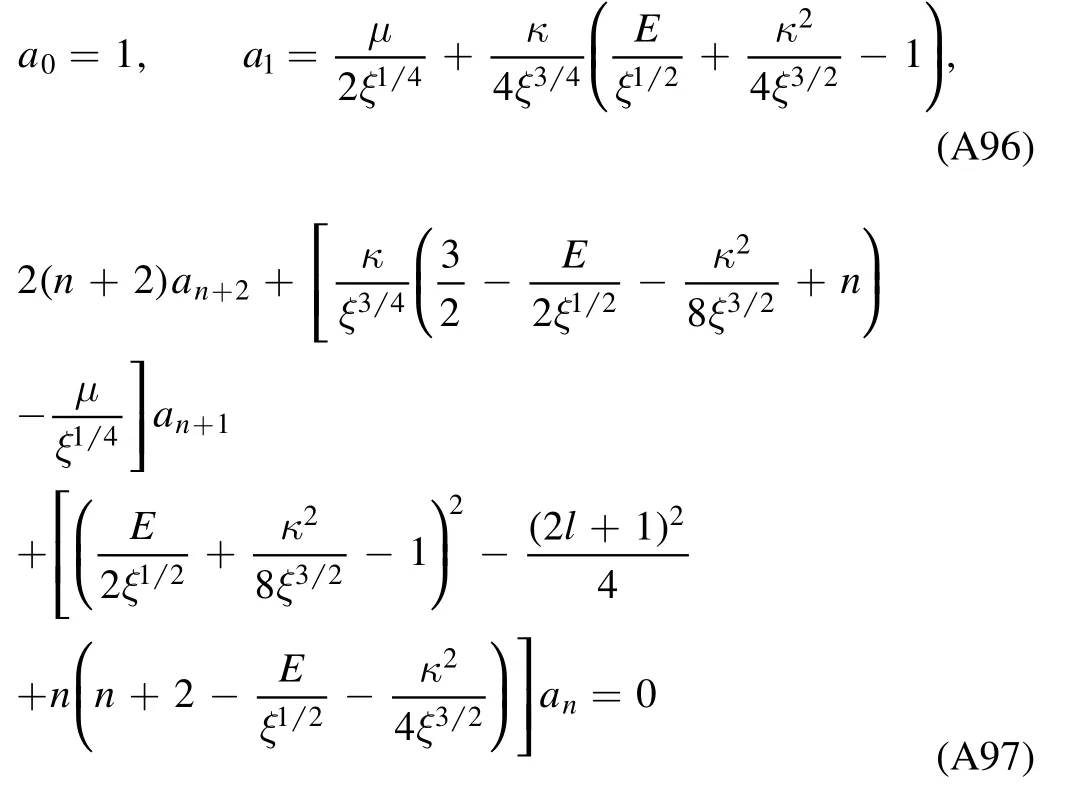
and
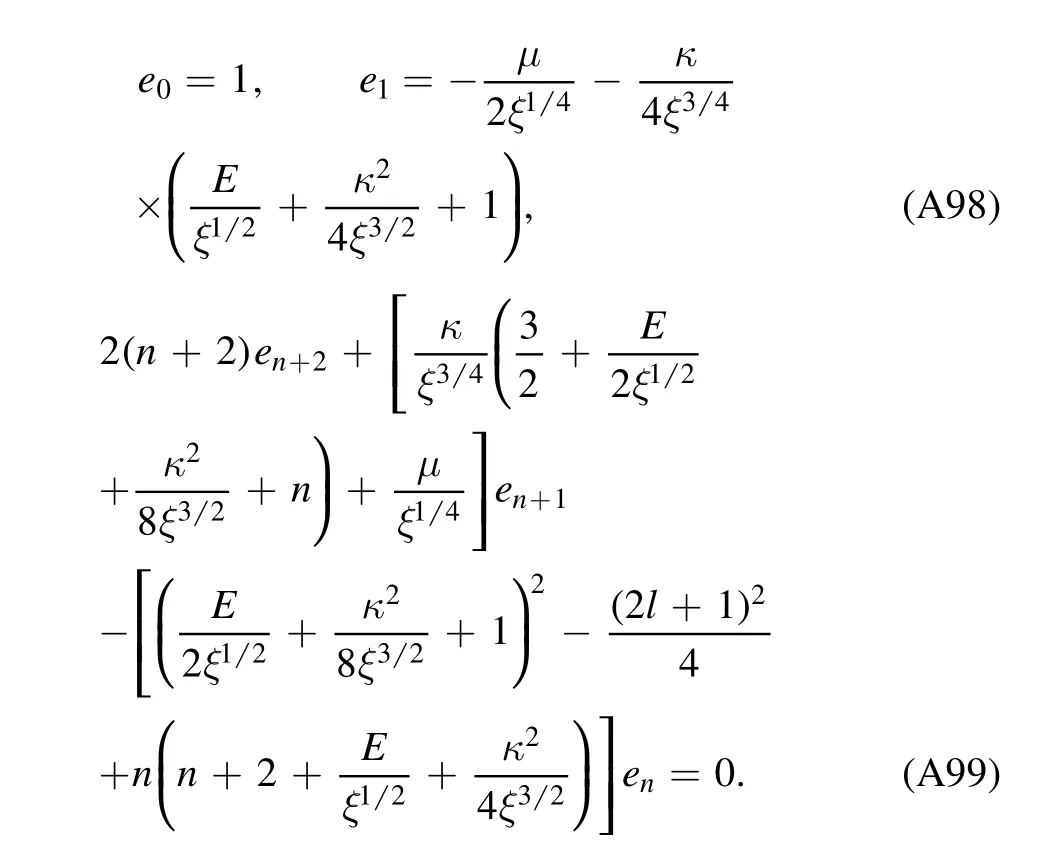
D.3.Eigenfunctions and eigenvalues
To construct the solution,we first express the regular solution(A93)as a linear combination of the two irregular solutions(A94)and(A95).
The regular solution(A93),with the relation[9,20]

and the expansions(A94)and(A95),becomes

The boundary condition of bound states,u(r)∣r→∞→0,re quires that the coefficient of the second term must vanish since this term diverges whenr→∞,i.e.,
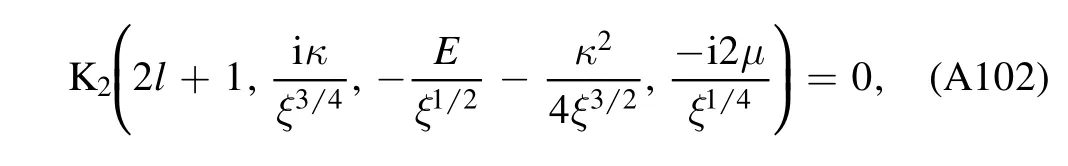
where

with

Equation(A102)is an implicit expression of the eigenvalue.
The eigenfunction,from equations(A101)and(A102),reads
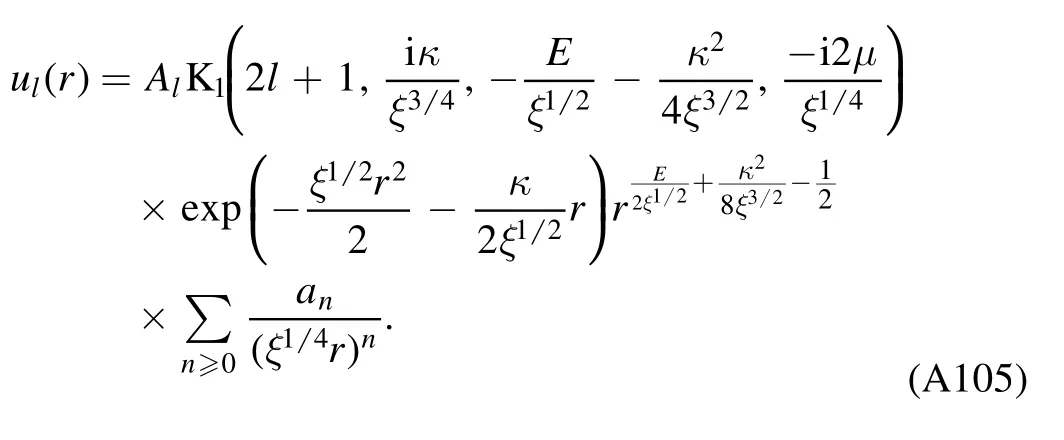
杂志排行
Communications in Theoretical Physics的其它文章
- Rogue waves of the sixth-order nonlinear Schrödinger equation on a periodic background
- Effects of magnetic field on the evolution of the wave function of a charged particle with an angular momentum
- Quantum information processing with nuclear spins mediated by a weakmechanically controlled electron spin
- Coherent control of spin tunneling in a driven spin–orbit coupled bosonic triple well
- Enhancing photon entanglement in a threemode optomechanical system via imperfect phonon measurements
- Variational quantum support vector machine based on Hadamard test
