Rogue waves of the sixth-order nonlinear Schrödinger equation on a periodic background

Wei Shiand Zhaqilao

1 College of Mathematics Science,Inner Mongolia Normal University,Hohhot 010022,China

2 Center for Applied Mathematical Science,Inner Mongolia,Hohhot 010022,China

Abstract In this paper,we construct the rogue wave solutions of the sixth-order nonlinear Schrödinger equation on a background of Jacobian elliptic functions dn and cn by means of the nonlinearization of a spectral problem and Darboux transformation approach.The solutions we find present the dynamic phenomena of higher-order nonlinear wave equations.

Keywords:rogue wave on a periodic background,sixth-order nonlinear Schrödinger equation,Darboux transformation,Jacobian elliptic function

1.Introduction

The nonlinear Schrödinger(NLS)equation plays a significant role in the field of nonlinear physics.It is a partial differential equation used to describe nonlinear waves and has a strict connection with many nonlinear physics problems,such as nonlinear optics,ion acoustic waves in plasma,and so on.

A ‘rogue wave’ means a strange wave with extremely large amplitude.It usually occurs in the ocean and comes out of nowhere and disappears without a trace[1],which may lead to a fatal catastrophe.However,at present,people still do not have an effective means of forecasting rogue waves accurately in advance.As a result,the study of rogue waves is necessary and relevant.Recently,some meaningful and important related papers have been published,such as[2,3].

In 1983,Peregrine[4]found the analytic expression for a rational solution of the NLS equation localized both in time and in space that is now known as the Peregrine breather.As was shown in 2009,this solution represented the first-order rogue wave of the NLS equation.Rogue waves have been studied in many fields,such as the ocean,optical fibers and Bose–Einstein condensates.Recently,Chenet al[5]studied rogue waves on a periodic background in 2018.Such rogue waves are a kind of wave formed on the periodic background of the Jacobian elliptic functions dn and cn.By means of the nonlinearization of a spectral problem[6]and the Darboux transformation approach[7–12],periodic standing waves of various equations have been investigated,such as the mKdV equation[13],the NLS equation[5,14–16],the fifth-order Ito equation[17],the sine-Gordon equation[18]and the Hirota equation[19].

Recently,studies related to higher-order rogue wave solutions of the NLS equation have been developing rapidly.For example,Zhanget al[20]constructed rogue wave solutions on the periodic background for the fourth-order NLS equation.Yueet al[21]investigated modulation instability,rogue waves and spectral analysis for the sixth-order NLS equation.In addition,many researchers have also considered the higher-order Schrödinger equations and their applications.For instance,Brocchiet al[22]investigated a class of sharp Fourier extension inequalities for fractional and higher-order Schrödinger equations.Duanet al[23]studied the unique continuation properties of the higher-order NLS equations and proposed exponential decay weighted estimates as well as anLp-type Carleman estimate based on the Littlewood–Paley theory.

In the past few years,there have been abundant studies with profound significance and advances in the higher-order NLS hierarchy.In 2015,Kedzioraet al[24]presented an infinite NLS equation hierarchy of integrable equations.In 2016,Ankiewiczet al[25]studied the infinite integrable NLS equation hierarchy and put forward the generalized Lax pair and various solutions.The infinite integrable NLS equation takes the following form:

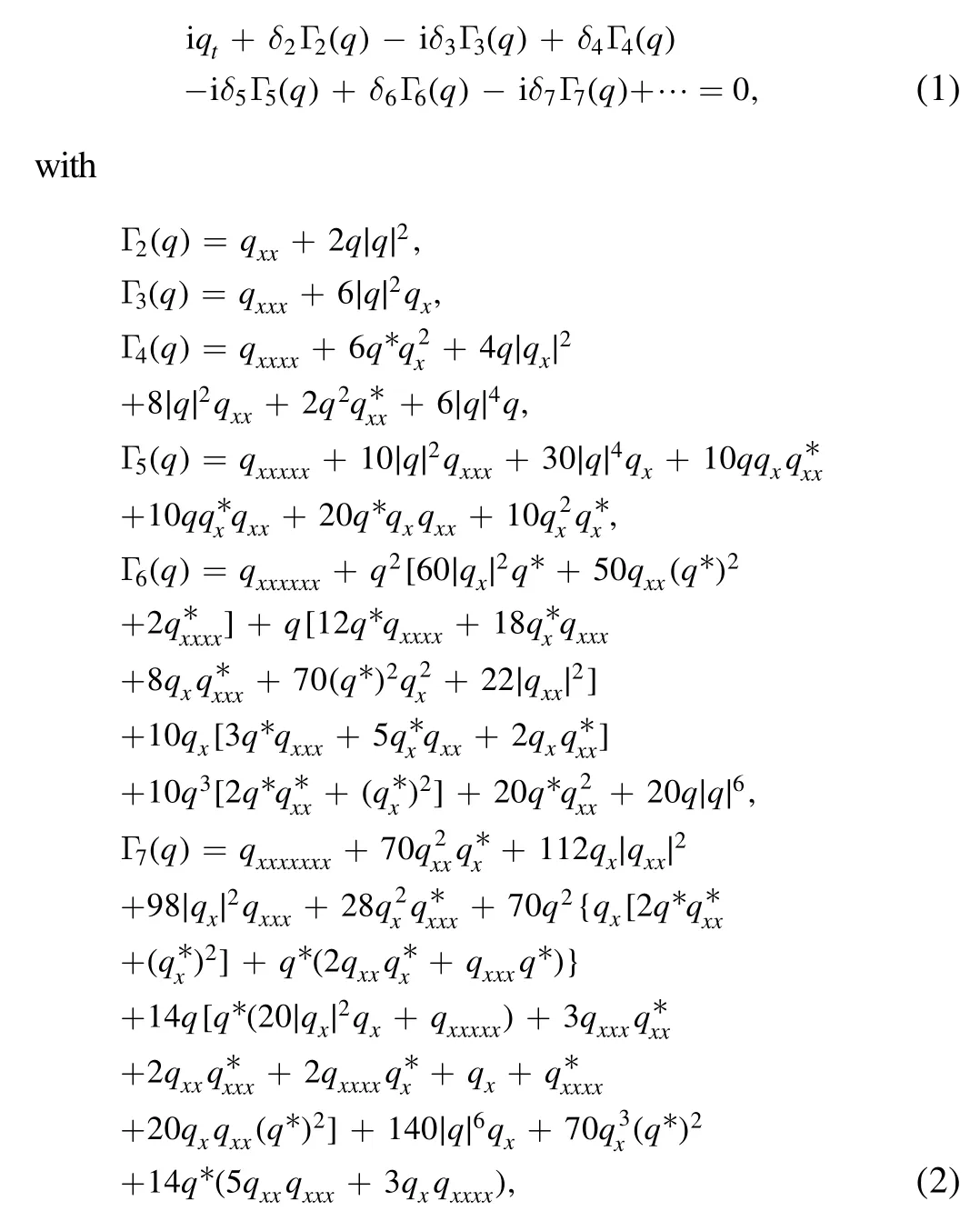
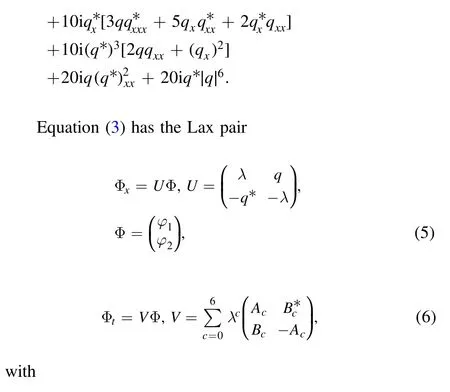
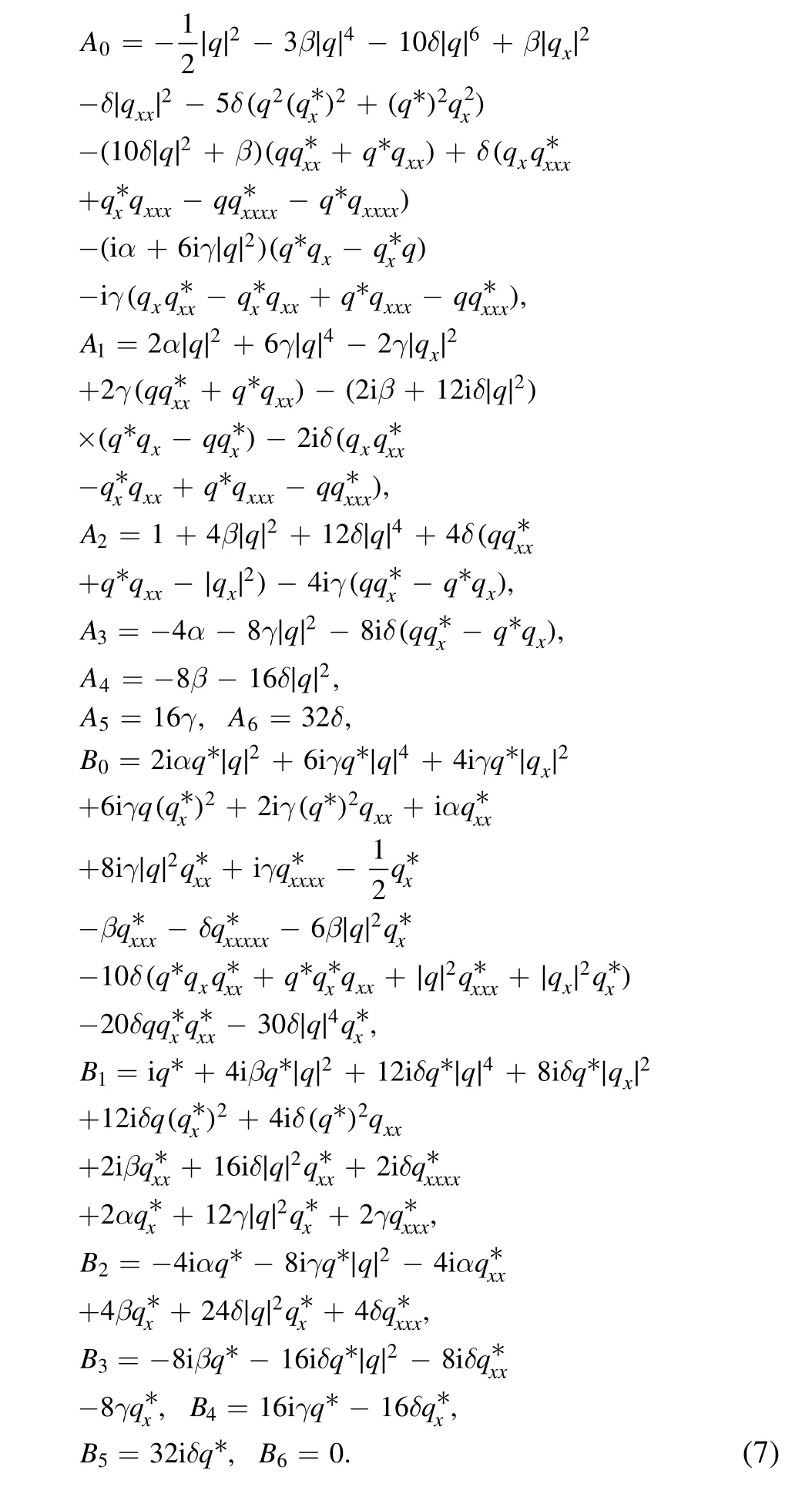
The compatibility conditionUt−Vx+[U,V]=0 of Lax pair(5)–(6)gives rise to equation(3).

To our knowledge,rogue wave solutions of equation(3)on a periodic background have not been constructed.Hence,in the rest of the paper,our purpose is to construct the rogue wave solutions of equation(3)on a periodic background through the nonlinearization of a spectral problem and the Darboux transformation approach.The structure of this paper is given as follows.In section 2,we deduce two families of periodic solutions called dn and cn for equation(3).In section 3,we nonlinearize the Lax pair of equation(3).In section 4,we obtain the periodic and non-periodic wave solutions of equation(3).In section 5,we use Darboux transformation to construct the rogue wave solutions of equation(3)on the dn-periodic background and cn-periodic background.In section 6,some conclusions are given.

2.Two families of periodic solutions of equation(3)

3.Nonlinearization of the Lax pair

4.Periodic and non-periodic solutions of the Lax pair

5.Rogue waves on the periodic background

5.1.Darboux transformation

5.2.Rogue waves on the dn-periodic background

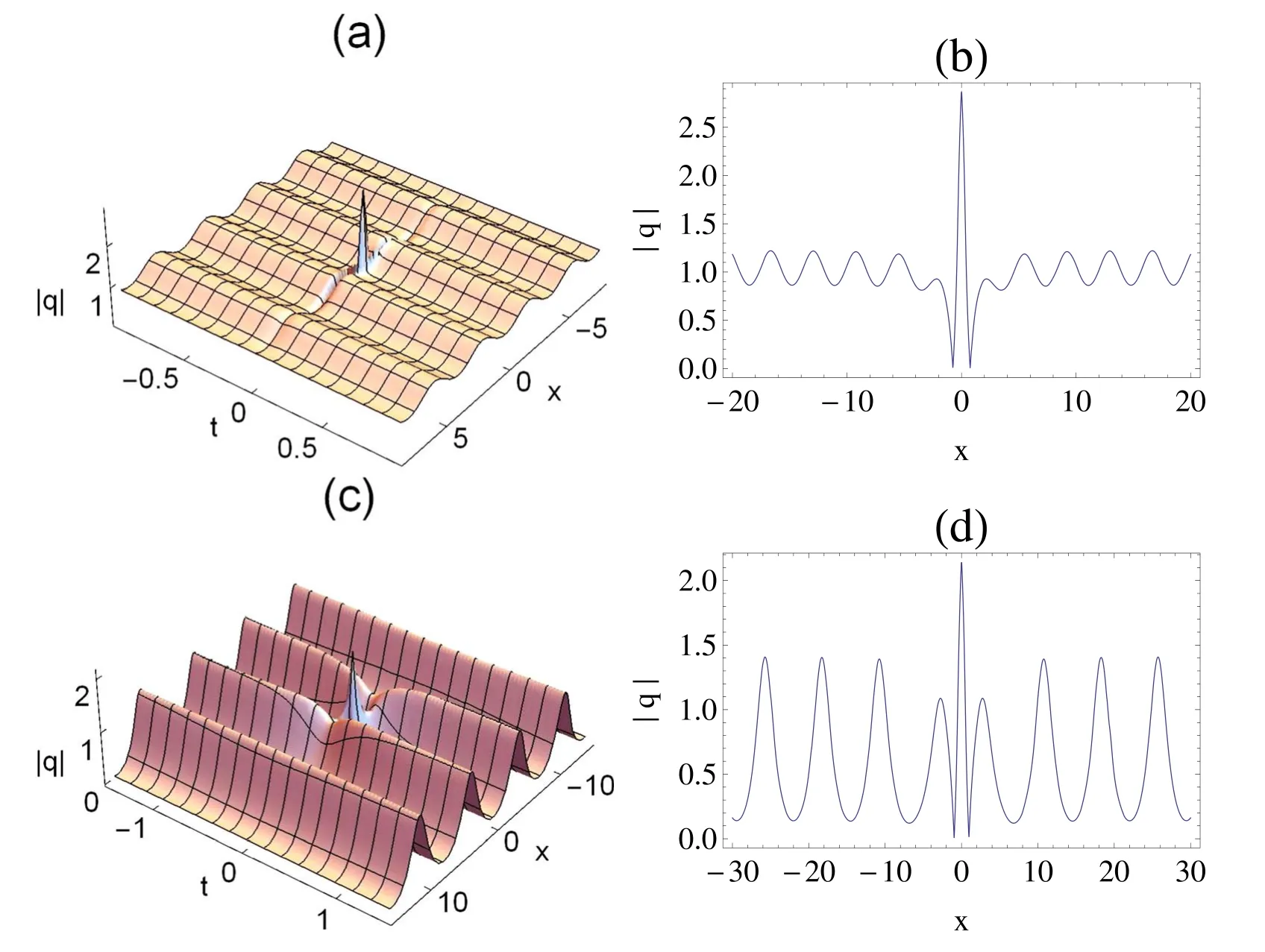
Figure 1.Rogue waves on the dn-periodic background with β=1,γ=3,δ=3,ϑ=0, k=0.5.(a)Three-dimensional plot,(b)transverse plot at t=0.Rogue waves on the dn-periodic background with β=1,γ=3,δ=3,ϑ=0, k=0.99.(c)Three-dimensional plot,(d)transverse plot at t=0.

5.3.Rogue waves on the cn-periodic background

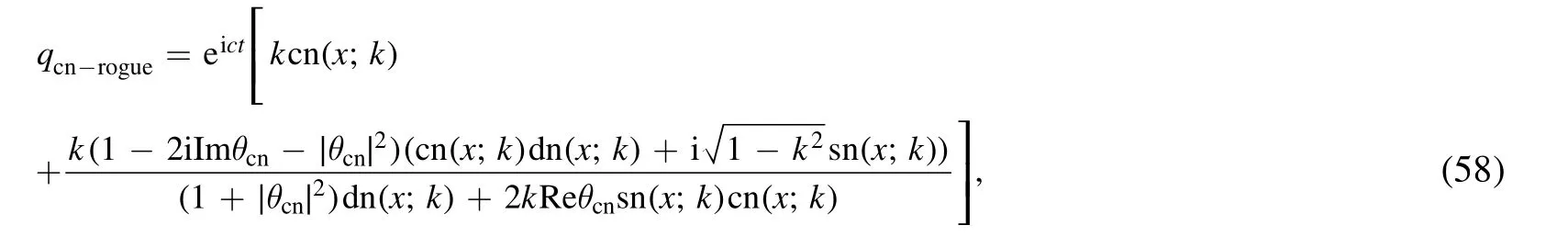
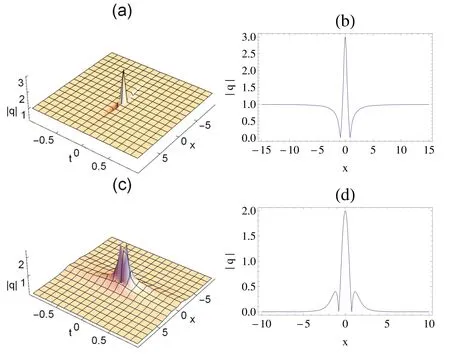
Figure 2.Degenerate rogue waves on the dn-periodic background with β=1,γ=3,δ=3,ϑ=0, k=0.(a)Three-dimensional plot,(b)transverse plot at t=0.Degenerate rogue waves on the dn-periodic background with β=1,γ=3,δ=3,ϑ=0, k=1.(c)Threedimensional plot,(d)transverse plot at t=0.

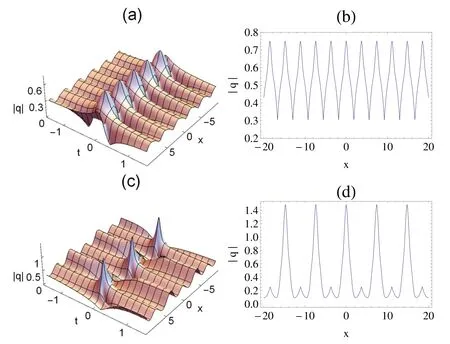
Figure 3.Rogue waves on the cn-periodic background with β=1,γ=3,δ=3,ϑ=0,k=0.5.(a)Three-dimensional plot,(b)transverse plot at t=0.Rogue waves on the cn-periodic background with β=1,γ=3,δ=3,ϑ=0,k=0.99.(c)Three-dimensional plot,(d)transverse plot at t=0.

Figure 4.Degenerate rogue waves on the cn-periodic background with β=1,γ=3,δ=3,ϑ=0, k=1.(a)Three-dimensional plot,(b)transverse plot at t=0.

with

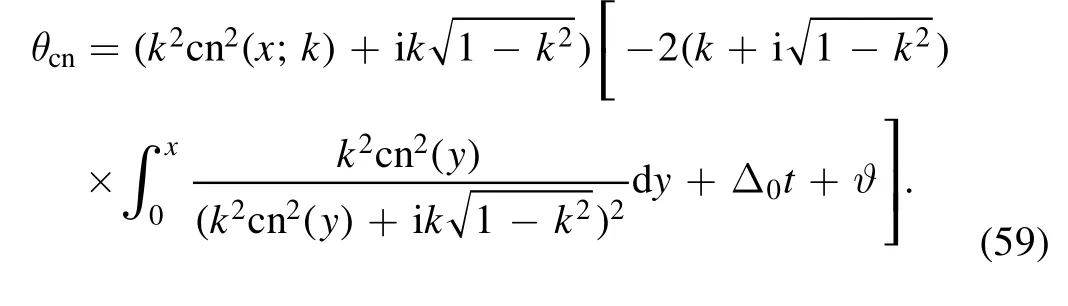
The rogue waves on the cn-periodic background(58)are presented in figures 3(a),(b)withk=0.5 and(c),(d)k=0.99.

In particular,whenk=1,we obtain the degenerate solution and present it in figure 4.

6.Conclusions

In this paper,the rogue waves of the sixth-order NLS equation on the periodic background of Jacobian elliptic functions dn and cn are constructed by means of nonlinearization of a spectral problem and Darboux transformation approach.If we compare the results in this paper to the results of some other well-known NLS equations such as[5,14–16],we find that all the above papers have similar expressions for solutions like(56),(58)and similar plots for solutions,which confirms the correctness of our results.However,our current study is just dependent upon the spectral problem in the AKNS system.In the future,we expect to construct rogue waves on a periodic background based on other spectral problems and we hope our results can provide some inspiration in the study of rogue wave phenomena on periodic backgrounds in the field of nonlinear physics.

Acknowledgments

This work was supported by the National Natural Science Foundation of China(Grant Nos.11 861 050,11 261 037),the Natural Science Foundation of Inner Mongolia Autonomous Region,China(Grant No.2020LH01010)and the Inner Mongolia Normal University Graduate Students Research and Innovation Fund(Grant No.CXJJS21119).

Conflict of interest

The authors declare that they have no conflict of interest.

ORCID iDs