Enhancing photon entanglement in a threemode optomechanical system via imperfect phonon measurements

Jing Qiu,Dongni Chen,Ying-Dan Wang and Stefano Chesi,4

1 Beijing Computational Science Research Center,Beijing 100193,China

2 CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,P O Box 2735,Beijing 100190,China

3 School of Physical Sciences,University of Chinese Academy of Sciences,No.19A Yuquan Road,Beijing 100049,China

4 Department of Physics,Beijing Normal University,Beijing 100875,China

Abstract By considering a 3-mode optomechanical system formed by two cavities interacting with a common mechanical mode,we demonstrate that phonon-counting measurements lead to a significant enhancement of entanglement in the output of the two cavities.This conclusion still holds for an inefficient detector,but the dependence on system parameters changes qualitatively from the ideal limit of perfect projective measurements.We find non-trivial optimal points for the entanglement as functions of detector efficiency,measurement outcome,and optical drive strengths.We characterize both the highest achievable entanglement as well as a‘typical’value,obtained at the most likely measurement outcome.Numerical results are well understood within an approximate analytical approach based on perturbation theory around the ideal detector limit.

Keywords:optomechanical system,entanglement concentration,imperfect phonon measurements,maximum entanglement,typical entanglement

1.Introduction

Optomechanical systems,in which electromagnetic radiation is coupled to the mechanical motion of vibrating elements[1,2],are of great interest for quantum information processing.Coherent control of photonic and mechanical degrees of freedom through radiation-pressure interaction has allowed remarkable achievements in mechanical ground-state cooling[3–5],generation of squeezing[6–10],and entangled states of mechanical and/or cavity modes[11–14].Among a variety of setups,we will focus here on the three-mode system illustrated in figure 1,where two cavities interact with a common mechanical mode.Of particular interest is that the two cavities can have very different frequencies.Significant advances in microwave-optical conversion have already been reported in such optomechanical systems[15,16],making it a promising interface between solidstate quantum information devices and fiber optics quantum communication[17–21].

The same optomechanical system is also effective in generating photon entanglement,which has been studied in detail theoretically[22–26]and was realized by a recent experiment[14].The output entanglement of the two cavities is the main focus of the present work.It can be optimized with respect to the optical drives[14,22],but further increases are possible through more sophisticated approaches.In particular,the tripartite entanglement of the full system(i.e.considering explicitly the output of the mechanical mode)diverges when approaching the instability point[22],suggesting that the large entanglement of the three-body state may serve as a physical resource to greatly enhance the bipartite entanglement of the emitted photons.

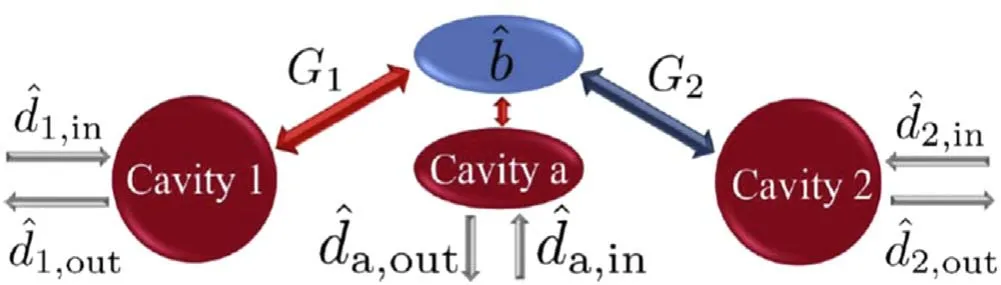
Figure 1.Schematics of the three-mode system,where two driven cavities(1 and 2)interact with a common mechanical resonator.Tripartite entanglement is generated in the output of these modes[22].An auxiliary cavity(a)can be used to read-out the mechanical output,leading to entanglement concentration for the emitted photons.

Although successful entanglement concentration and distillation protocols have been developed for discrete-level systems[27,28],the entanglement of continuous-variable Gaussian states cannot be distilled using Gaussian operations[29,30].Here,due to the quadratic nature of the linearized optomechanical interactions,the output state is a squeezed thermal state[22]and optomechanical non-linearities are generally small[31],making it difficult to implement non-Gaussian operations at the Hamiltonian level.An attractive alternative is offered by phonon-counting measurements,which have been shown to enhance the cavity output entanglement in an idealized scenario of perfect projective measurements[26].As illustrated in figure 1,phonon-counting can be realized by coupling the mechanical mode to a strongly damped auxiliary cavity,which can then be used to indirectly measure the phonon number through standard photon counting techniques[22].Recently,this strategy was successfully realized[32].

In the present work we analyze the robustness of phonon measurements as a simple entanglement concentration protocol,by including the(possibly large)detector inefficiency.This issue is especially important in view of the combined experimental progress of[14,32].We demonstrate that phonon-counting is always beneficial,even with limited detector efficiency,and determine the optimal conditions to enhance photon entanglement.We discuss both the maximum entanglement upon post-selection,as well as its typical value versus system parameters.Numerical results are well understood through an approximate analytical approach.

2.Output entanglement

We start by summarizing previous results on the output entanglement of a 3-mode optomechanical system,formed by two cavity modes with frequencies ω1and ω2coupled simultaneously to a mechanical mode with frequency ωm.The setup is illustrated in figure 1 and can be described by the Hamiltonian

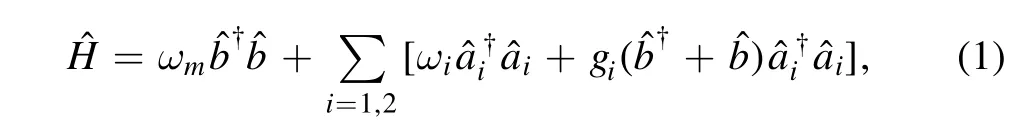
Figure 2.Entanglement versus the detected phonon number q.The upper red dots refer to an ideal projective measurement,i.e.μ=1,and are well approximated by the solid curve,given by equation(12).The other dotted curves refer to μ=0.99,0.9,0.8,0.6,0.4,and 0.2(from top to bottom).It can be seen that,after measurement, EN(μ, q)is always larger than equation(6)(the entanglement before measurement),marked by the horizontal dashed line.The crosses are estimated positions of the entanglement maxima,see the main text.Other parameters are C1=10 and C2=3,giving Nm ≃0.19.

whereqis the result of the measurement and

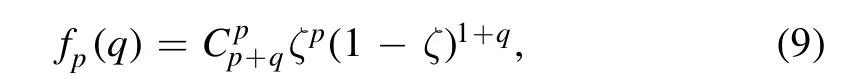
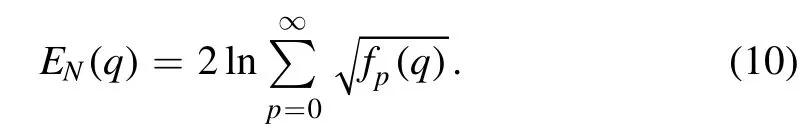
An interesting observation is that the projected state|Ψq〉always has a larger photon entanglement than the original state before measurement.This is shown in figure 2,where the upper(red)dots were computed assuming an ideal phonon detector.We see thatEN(q)is an increasing function ofqwhere theq=0 value is already larger than equation(6):

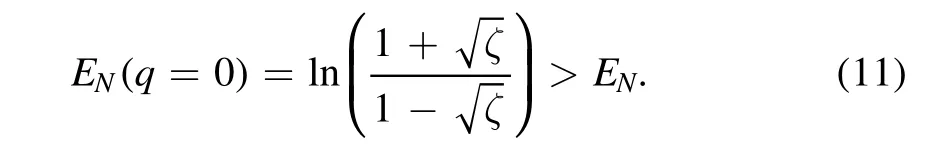
Therefore,projective measurements yield a conceptually simple,yet nontrivial,entanglement concentration protocol.Note that the state before measurement is a statistical mixture of all the|Ψq〉states,where any|Ψq>0〉has larger entanglement than|Ψq=0〉.Still,purification to the lowest-entanglement state of the mixture is beneficial.For an ideal detector,the growth of entanglement can be characterized through a large-qGaussian approximation offp(q),see[26]and equation(A1),yielding:

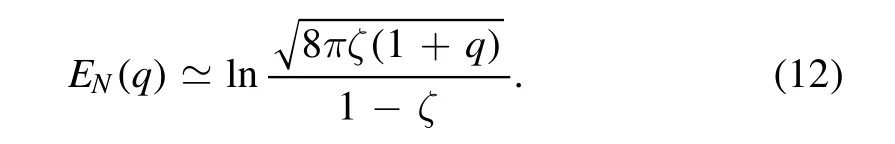
We see that not only the entanglement is larger than before the measurement,but grows logarithmically with the number of detected phonons and,in principle,can be as large as desired(by postselecting on the measured value ofq).A comparison between the exact and approximate dependence onqis shown in figure 2.

3.Inefficient phonon detecti on

As the phonon measurements are necessarily imperfect,it is important to take into account a finite detection efficiency rather than assuming ideal projective measurements.As mentioned,the mechanical output can be mapped to the output of an auxiliary cavity.Therefore,following the standard treatment of photodetection[36,37],we introduce phonon-counting operators:

While the case of an ideal detector is particularly straightforward[see[26]and equation(10)],computingEN(μ,q)at finite efficiency can be very cumbersome.The numerical evaluation is helped by the natural block-diagonal structure of,described in appendix A.Representative numerical results are shown in figure 2.We see that,as expected,the entanglement is reduced by a smaller μ.However,the phonon detection is still effective for entanglement concentration,sinceEN(μ,q)is always larger than the entanglementENbefore measurement(dashed line).Another interesting remark is that the dependence onqis modified qualitatively by the detector inefficiency:EN(μ,q)becomes non-monotonic when μ<1,and attains its maximum value at an optimal number of detected phonons.

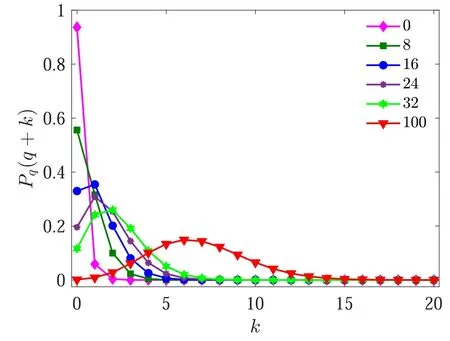
Figure 3.Probability distribution Pq(q+k)at different values of the detected phonon number q,as indicated by the legend.Other parameters are C1=10, C2=3,and μ=0.6,giving ε ≃0.063.

The dependence of the maximum on system parameters can be characterized in more detail through an approximate analytical treatment.For the moment,we give a qualitative discussion of the optimalqbased on the phonon probability distribution in the postselected state.After measurement,the statereads:

Figure 4.Maximum entanglement as a function of μ.The dashed curve is obtained numerically.The red curve,given by equation(21),is in excellent agreement with the exact numerical result.We also show the upper and lower bounds of equation(22).Here,like in figure 3,we used C1=10 and C2=3.

In the above estimates,we neglected the constant correction to the logarithmic divergence.The divergence of the maximum entanglement in the ideal detector limit is directly related to the logarithmic divergence ofEN(1,q)in the limit of largeq.

4.Analytical approach

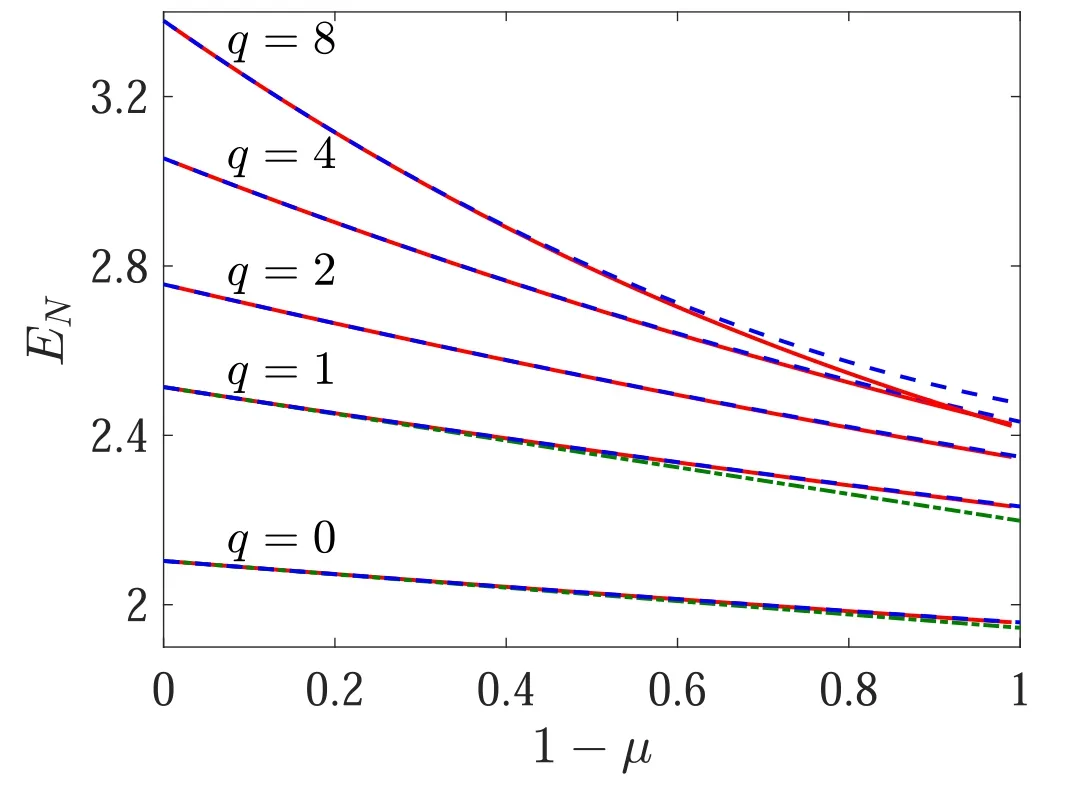
Figure 5.Entanglement versus detector efficiency μ.The numerical results(red solid curves)are compared to equation(28).The dotted–dashed curves only include the first correction,linear in μ.The full equation(28),with the quadratic term,is plotted as blue dashed curves.Here C1=10 and C2=3.

which is consistent with equation(19).

A comparison between equation(28)and the numerical results is shown in figure 5,for a specific choice ofC1,C2and relatively small values ofq.We see that the leading term(i.e.the simple linear correction)describes the initial decrease of entanglement away from μ=1 well.However,deviations appear at smaller μ,when nonlinear corrections start to play an important role.This effect is captured by the quadratic terms of equation(28),which give much better agreement over the whole range of μ.We note that,although the expansion is performed for ‘small’ deviations from the ideal detector limit,the appropriate expansion parameter is(q+1)ε and not 1 −μ.Therefore,the expansion is still valid for a very poor detector with 1 −μ∼1,if ε ≪1 andqis sufficiently small.

Further comparison of the analytic and numerical results as a function ofqis shown in figure 6.Besides confirming that the second-order terms generally improve the agreement,we see that the series becomes unreliable atq∼1/ε,consistently with previous remarks.Interestingly,the exact numerical results always lie between the first- and secondorder approximation,thus the expansion appears to be formed by terms with alternating signs or,at least,the third-order term is negative.

The latter observation is useful to estimate the entanglement aroundq∼1/ε ≫1,which is at the boundary of validity of the perturbative expression.This value ofqis interesting because it approximates the optimal point for the output entanglement[see the discussions of the previous section and,in particular,equations(20)and(21)].In appendix B we analyze the coefficient of the second-order term atq≫1 and obtain[see equations(B4)]:

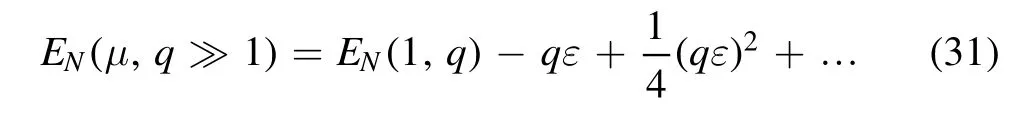
Combining this simplified expression with equations(20)we obtain the upper and lower bounds of equation(22).See also figure 4 for a quantitative check.While the lower bound only takes into account the first-order term,the upper bound includes both the first- and second-order corrections and is a more accurate estimate of the true value.

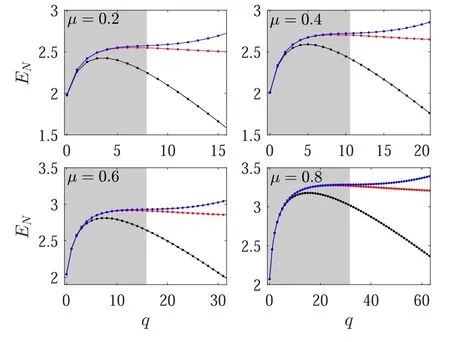
Figure 6.Further comparisons of the perturbation theory of EN with exact numerical values(red middle curve).The upper(lower)curve is a plot of equation(28)with(without)the term quadratic in ε.The shaded area marks the region q<1/ε,beyond which equation(28)is not applicable and large deviations appear.In these plots,C1=10 and C2=3.

5.Typical entanglement

So far,we have mainly analyzed the maximum entanglement which can be obtained with an imperfect detector.However,this quantity is not always a practical characterization ofEN(μ,q).As the probability of detecting a large number of phonons decreases quickly withq,it might be very difficult to generate a maximally entangled state.More precisely,the probability distribution of phonon detection outcomeqis:

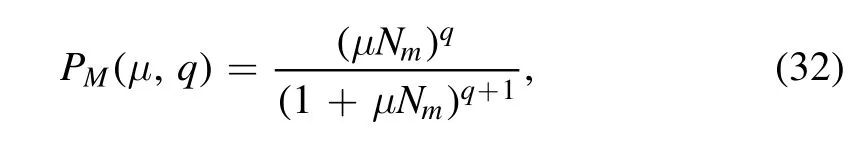
which gives an average number μNmof detected phonons.In the specific case of figure 2,we haveNm≃0.2,thus it is very difficult to get a value of entanglement much larger thanEN(μ,q=0)∼2.This motivates us to introduce the ‘typical’entanglement,defined as follows:

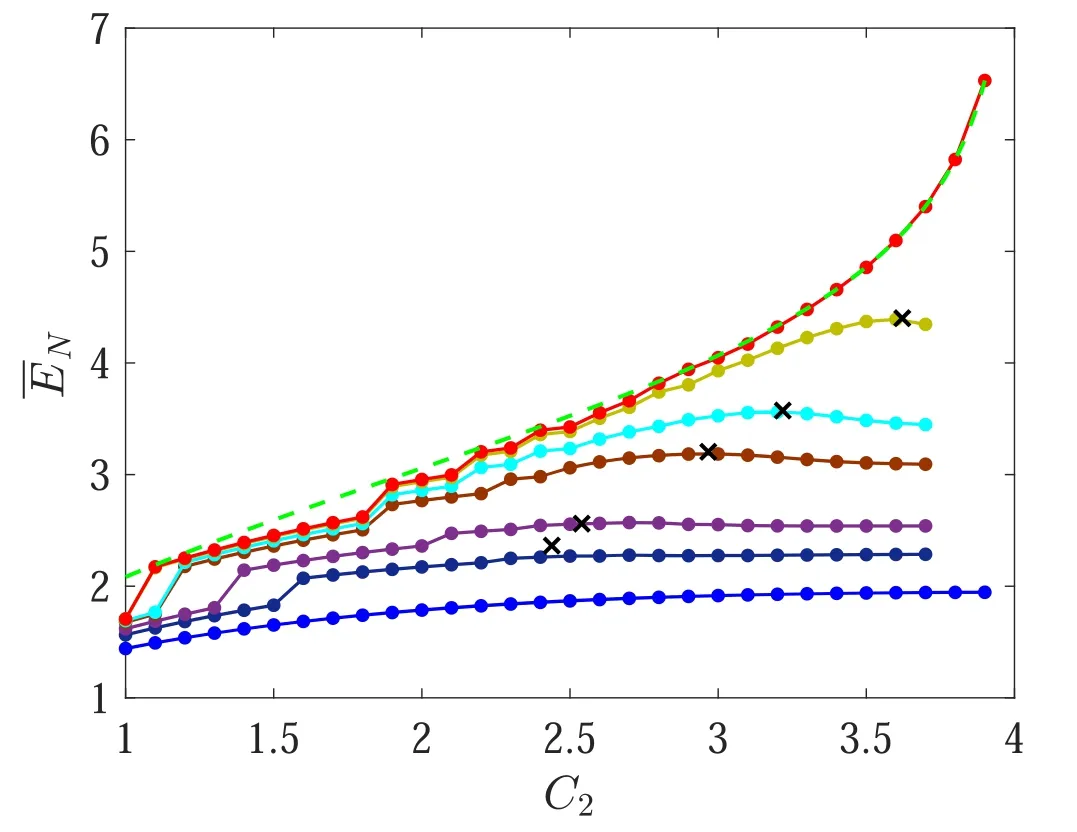
Figure 7.Dependence of the typical entanglement on C2 for different detector efficiencies μ.The baseline data(bottom blue dots)are the entanglement before measurement.The other sets of data are for μ=1,0.99,0.95,0.9,0.7 and 0.5(from top to bottom).The green dashed curve is equation(34),approximating μ=1.The crosses are estimates of the maxima,given by equations(36)and(37).Here, C1=3.

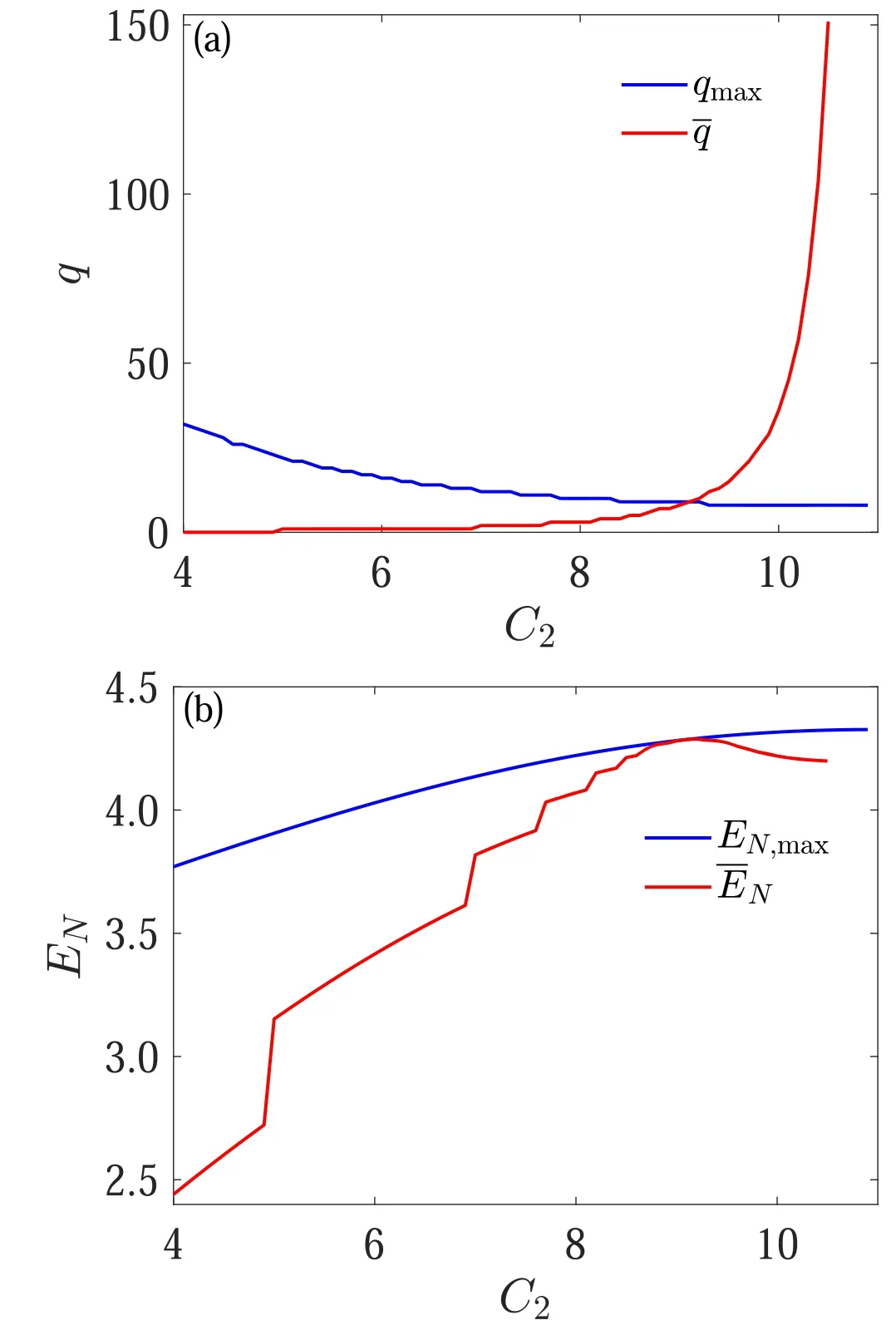
Figure 8.Comparison between typical entanglement and maximum entanglement,as function of C2 at fixed C1=10 and μ=0.9.Panel(a)shows the dependence of and qmax on C2.Panel(b)compares the values ofand.The curves in panel(a)meet when,which corresponds well to the maximum ofshown in panel(b).

6.Discussions and conclusion

In this work,we have investigated an entanglement concentration scheme applicable to a 3-mode optomechanical system,where the entanglement between emitted photons can be enhanced through phonon counting measurements.Motivated by recent experimental progress[14,32],we have analyzed in detail the role of detector inefficiency.We find that the entanglement concentration scheme is generally advantageous,also considering a poor efficiency.Furthermore,we have obtained the maximum value of entanglement as a function of the measurement outcomeq.The optimalqmight be quite different from the most likely measurement outcome,which motivates us to discuss how the ‘typical’entanglement depends on system parameters.

This scheme takes advantage of the strong tripartite entanglement before measurement.In the absence of phononcounting,the bipartite entanglement is maximized whenC2→C1+1 but remains finite,even if the system is approaching the unstable regime.This is possible as the two optical modes are strongly entangled with the mechanics,and a divergence can only be found by considering the genuine tripartite entanglement[22].Phonon-counting measurements are able to recover the hidden entanglement,i.e.they transform effectively the tripartite correlations into a bipartite entanglement for the outgoing photons.For an ideal projective measurement,the concentrated bipartite entanglement leads to a diverging behavior when approaching the instability(both in the maximum and typical entanglement).Such divergence is cut-off by a finite detector efficiency,which makes the optimal operation point nontrivial.

Acknowledgments

S C acknowledges support from NSFC(Grants No.11974040 and No.12150610464),and NSAF(Grant No.U1930402).Y D W acknowledges support from MOST(Grant No.2017YFA0304503).

Appendix A.Numerical evaluation of entanglement

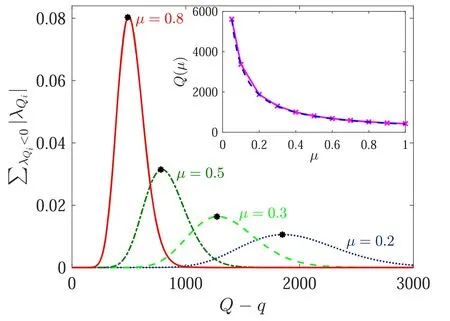
Figure A1.Sum of negative eigenvalues in every subblock Q,for various detector efficiencies μ.The stars,given by equation(A4),are the approximate values Q yielding the largest value of.In the inset we find numerically the Q maximizing(solid curve),and compare it to the approximate value equation(A4)(dashed curve).Other parameters are C1=10, C2=10,and q=20.

Appendix B.Perturbation theory

ORCID iDs