Quantum information processing with nuclear spins mediated by a weakmechanically controlled electron spin

Wan-Jun Su and Guang-Zheng Ye

Department of Physics,Fuzhou University,Fuzhou 350002,China

Abstract We propose a scheme to achieve nuclear–nuclear indirect interactions mediated by a mechanically driven nitrogen-vacancy(NV)center in a diamond.Here we demonstrate twoqubit entangling gates and quantum-state transfer between two carbon nuclei.When the dipole–dipole interaction strength is much larger than the driving field strength,the scheme is robust against decoherence caused by coupling between the NV center(nuclear spins)and the environment.Conveniently,precise control of dipole coupling is not required so this scheme is insensitive to fluctuating positions of the nuclear spins and the NV center.Our scheme provides a general blueprint for multi-nuclear-spin gates and for multi-party communication.

Keywords:dipole–dipole interaction,mechanically control,NV center,quantum Zeno effect

1.Introduction

Solid-state quantum systems are advantageous for quantuminformation applications due to their inherent amenability to scaling[1].Weakly coupled to the environment,nuclear spins have a long coherence time in comparison with those of electron spins.Thus,nuclear spins are especially attractive for solid-state quantum storage[2]and for quantum gates[3].Unfortunately,direct nuclear dipole–dipole interaction is negligible,which necessitates alternatives to coupled nuclear spins.

A nitrogen-vacancy(NV)center in a diamond is a promising platform for highly sensitive nanoscale sensors[4,5].The NV center electronic spin has exceptional quantum properties including high sensitivity to external signals[6],and a long spin coherence time[7].Additionally,NV center spin states can be prepared and read out by optical pulses or microwave pulses at room temperature[8].These properties make NV center spin sensors an attractive candidate to detect nuclear–nuclear interactions[9–11],and open up a way to exploit its applications to solid-state quantum information.Recently,Chenet alused periodical resets of an NV center to protect a nuclear quantum sensor against decoherence and relaxation of the NV center[12].Via an extra auxiliary NV center electronic spin,we propose a scheme to control and mediate an effective nuclear dipole–dipole indirect interaction.

Driving spin transitions of an NV center is the key to using NV center spins for nuclear-spin sensing.Except for optical and magnetic pulses,mechanical driving is usually applied to spin control.Significant progress in integrating NV centers with micro-electromechanical systems has paved the way for spins coupled to mechanical resonators[13–17].Using mechanical driving,MacQuarrieet aldemonstrated direct spin-phonon interactions at room temperature as a means to drive magnetically forbidden spin transitions[18].

However,to achieve the nuclear–nuclear indirect interaction,two crucial challenges remain to be addressed:(1)disorder in spin positioning and(2)small stress-coupling coefficients in driving spin transitions.Here we present an approach to overcome these challenges,to thereby achieve high-fidelity twonuclear quantum gates and quantum-state transfer.In our scheme,an NV center is a mediator,coupling two nearby nuclear spins via dipole–dipole interactions.At the same time,mechanical(stress)wave is used to drive the magnetically forbidden spin transitionof the NV center spins.Our physical model requires that the driving-field Rabi frequency is sufficiently weak relative to the dipole-coupling strength.In experiments,normally,the stress-coupling coefficient is small so that large stress is required to produce a driving field[18].However,the small stress-coupling coefficient is helpful for our scheme,and large stress is not required,which increases the experimental feasibility.What’s more,desired conditional manipulations do not require precise control of the dipole coupling.Hence,our scheme is robust against variations and uncertainties in the positions of the NV center and nuclear spins.

This paper is organized as follows.Section 2 presents our physical model and the quantum dynamics of the model.In section 3 we propose a scheme to achieve entangling gates and quantum-state transfer based on this dynamics.We investigate fidelities versus parameter fluctuations(scaled Rabi frequency,dipole–dipole coupling strength,etc.)via numerical simulations.Section 4 presents the discussions of our physical model at ambient conditions and further applications.Section 5 is our conclusion.

2.Physical model

To model the system’s dynamics,decoherence effects,such as the spontaneous decay of the NV center and nuclear spin with the corresponding relaxation rate ΓNV,ΓN,and the dephasing effect,are taken into account.We assume that the correlations of the spin bath degrees of freedom vanish on a short time span,which is negligible compared to the characteristic time scale of the system dynamics[23].The memoryless(Markovian)environment then enables one to derive simple equations of motion with the Lindblad formalism,leading to the following master equation[24]

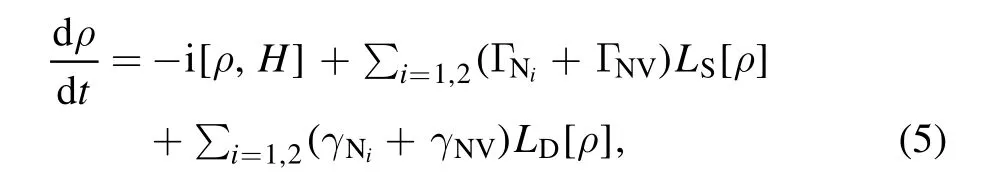
with the general form ofL[ρ]

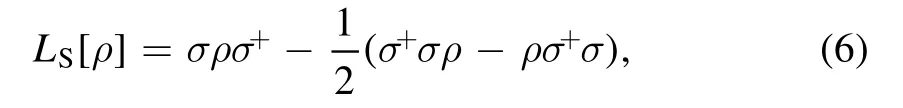
and

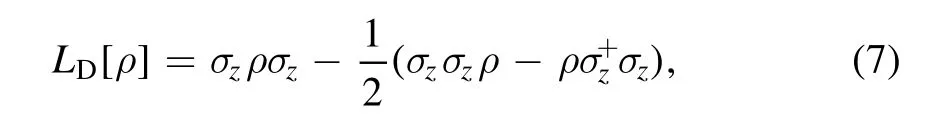
corresponds to the relaxation and dephasing effect of electron spin or nuclear spins.Here,σ is the dipole operator as σαβand σz=|↑〉〈↑|−|↓〉〈↓|.The spontaneous decay rate ΓNV∼1 KHz,ΓN∼1 KHz[25].The pure dephasing rate of the NV spin and nuclear spin γNV∼1 KHz,γN∼1/3 KHz[26].In the following numerical simulation,we consider that Γ=ΓNV=ΓNand γ=γNV=γNfor simplicity.

During the system dynamics,the system is initially in the state|Ψ0〉,and then evolves under equation(3)for a choosing time,resulting in a final density ρ.The fidelity is defined as[27]

whereρ=∣ψt〉〈ψt∣.In the following,we show how to achieve the quantum entangling gates and quantum state transfer based on this model.

3.Quantum information processing

3.1.Two-qubit entangling gate

Recently,Leonardoet alproposed a s cheme to realize nonperturbative entangling gates between distant qubits using uniform cold atom chains[28].In their work,an ideal mirror inverting dynamics generates a quantum gateGbetween qubitAand qubitB,which reads

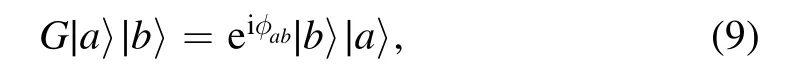
wherea,b∊{↓,↑}in the computational basis.In the following section,we show how to achieve the two-qubit entangling gate based on our physical model.

We assume that quantum information is encoded in nuclear spin states|↑〉Nand|↓〉N,and the NV center electron spin is an ancillary system,which is initially prepared in|f〉NVstate.For simplicity,we suppose there is only single excitation during the whole system’s evolution[29].Considering an initial system state|↑1↑2〉N|f〉NV,no dipole–dipole interaction takes effect.Time evolution of the system is within the subspace{|↑1↑2〉N|f〉NV,|↑1↑2〉N|↑〉NV}.The driving field only causes a single-qubit rotation.After a single Rabi cycle,the nuclear spin state returns to its original state timing a π phase shift.

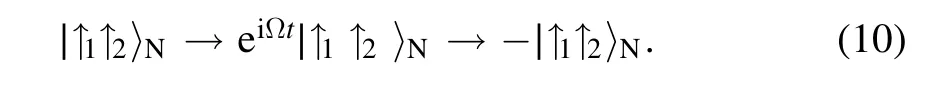
When we consider an initial system state|↑1↓2〉N|f〉NV,the whole system evolves in a single-excitation subspaceS1spanned by

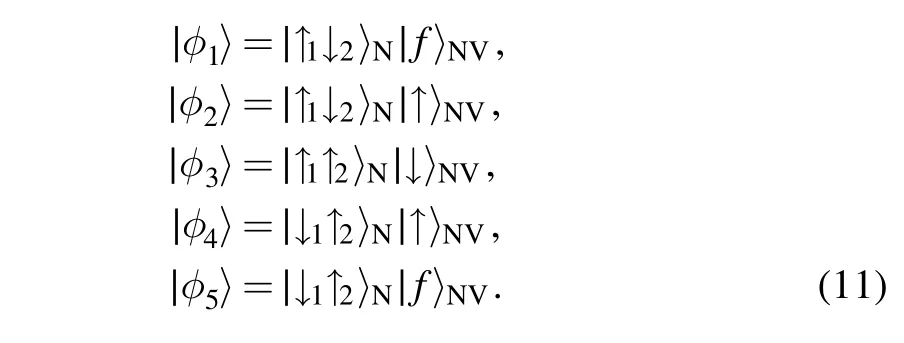
The Hamiltonian of this subsystem reads

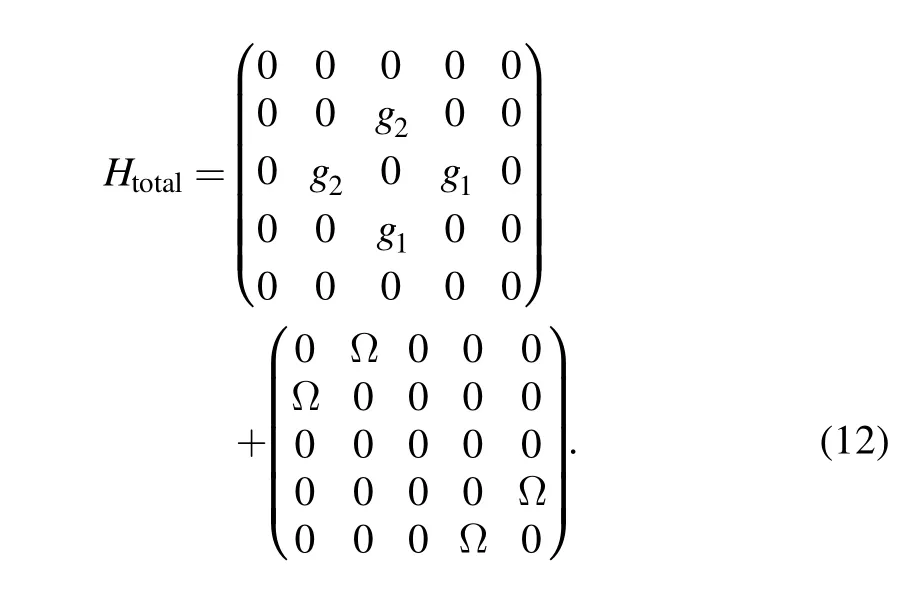
Then,settinggi=g,under the condition Ω ≪g,the whole Hilbert subspace is split into three invariant subspaces according to the degeneracy of eigenvalues ofHDD,

Therefore,the Hamiltonian in equation(4)is approximately dominated by

which corresponds to a two-qubit entangling gate between the distant nuclear spins.The ancillary system(NV center),initially prepared in|f〉NVstate,is entangled with the logical qubits during the gate operation,becoming once again disentangled by the end of the operation.

To verify the analytical results,we use numerical simulations to find the influences of the interaction.Our model is valid when Ω ≪g.Thus,we should consider the influence of the ratio Ω/gon the fidelity of the entangling gate.Figure 2 presents the fidelity as a function of Ω/gdisregarding the decay.Not surprisingly,the fidelity decreases as the ratio Ω/gincreases.The fidelity is 0.98,even when Ω/g=0.15.However,the interaction periodT=π/Ω depends on Ω,then a smaller ratio Ω/gresults in longer operating time and increased decoherence.To balance the fidelity and the operating time,we chooseg∼2π×2 MHz and Ω∼2π×210 kHz to satisfy Ω/g=0.1 in the following discussions.

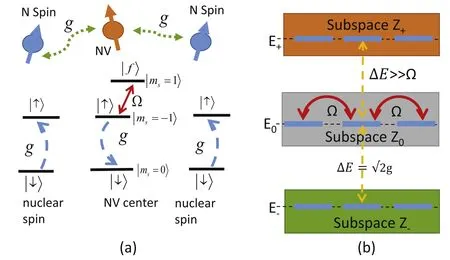
Figure 1.(Color online)(a)Illustration of the basic principle of an indirect interaction between two nuclear spins mediated by an NV center.The interaction between the NV center and nuclear spins occurs via coupling dipoles on the transition∣↑〉↔∣↓〉,with coupling strength g.The transition∣f〉↔∣↑〉of the NV center is resonantly driven by the mechanical(stress)wave of Rabi frequency Ω.(b)Schematic Hilbert subspaces.Due to the dipole–dipole interaction,the system energy is split into three energy levels{Z+, Z0, Z−}.The energy splitΔ E=g≫Ω.The interaction between different states during the same subspace via the driving mechanical wave(denoted by red dotted lines).

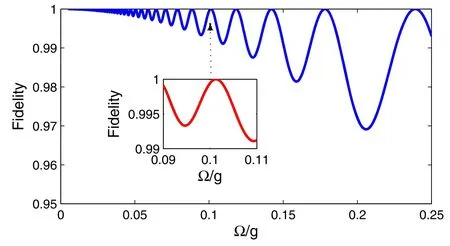
Figure 2.(Color online)The influence of the ratio Ω/g on the fidelity of the two-qubit entangling gate under ideal conditions.Ω/g ∊[0.005,0.25]and γN=γNV=0.

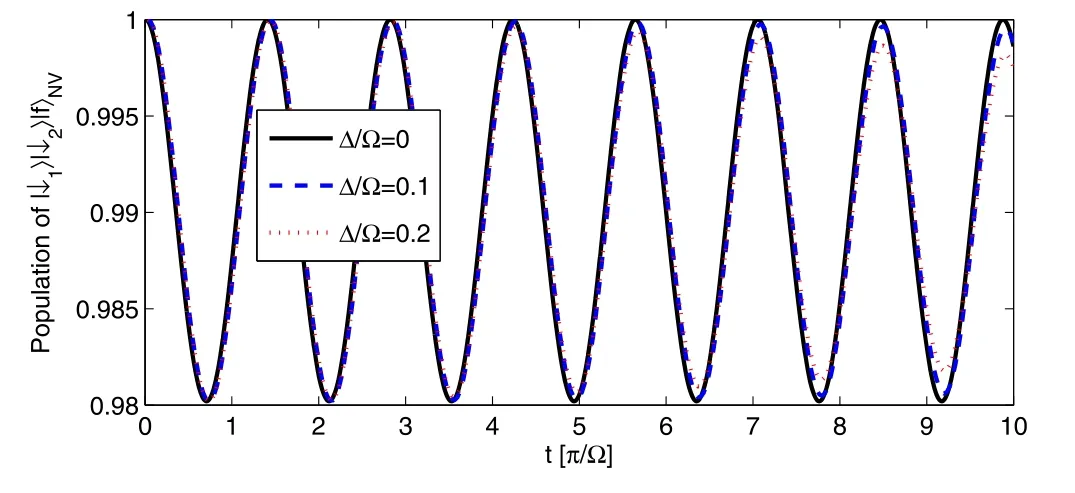
Figure 3.(Color online)The population of|↓1↓2〉N|f〉NV as a function of the scaled time,considering the influence of detuning.The scaled ratio Δ/Ω ranges from 0 to 0.5,γN=γNV=0,with g∼2π×2 MHz and Ω∼2π×210 kHz.

Figure 4.(Color online)The influence of decoherence on realization of the two-qubit entangling gate,for g∼2π×2 MHz and Ω∼2π×210 kHz.(a)Dynamical evolution of the populations during the gate operation,with γN/g=γNV/g=0.001.(b)The fidelity of the entangling gate versus γNV/g and γN/g.

The manipulation time depends on the stress-wave Rabi frequency.In our model,the NV center resonantly interacts with the driving field of frequency ωdrive,and the corresponding transition energy of|f〉NV↔|↑〉NVis ħω↑f.However,under ambient conditions,the quantum dynamics are affected by the off-resonant coupling,which will cause errors(phase shifts).We add a fluctuating term in the driving field,soHdrivecan be rewritten as

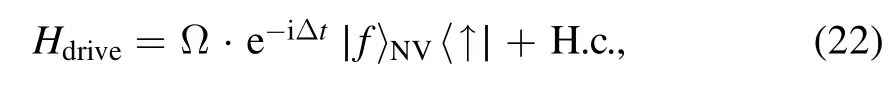
where Δ:=ω↑f−ωdrivedescribes the off-resonant coupling.The population of state|↓1↓2〉N|f〉NV,as a function of the interaction time and scaled off-resonant coupling Δ/Ω,is shown in figure 3.When the requirement Δ/Ω<0.2 is met,small fluctuations in the population occur.Considering a small deviation of the resonant interaction between the driving field and NV center,we find that the average gate fidelity equals 0.995 with Δ/Ω=0.1.The entangling gate is robust against fluctuations of the driving field,which is important to suppress errors.

The analysis above disregards the effects of decay.We now analyze how the gate operation is affected by desired dissipation according to equation(5).Assuming scaled spontaneous decay rates γN/g=γNV/g=0.001,figure 4(a)displays the dynamics of populations of nuclear spins states as a time function.At the end of interaction timeT,andare about 0.985.As shown in figure 4(b),the fidelity remains high(>0.96)with small-scaled decay rates γNV/gand γN/g,implying that the driving decouples the NV spin from the unwanted influence of the environment.

3.2.Quantum-state transfer

Reliable quantum-state transfer(QST)between distant qubits has become a significant goal of quantum physics research,owing to its potential application in scalable quantum information processing[30–33].If the system is initially in the state

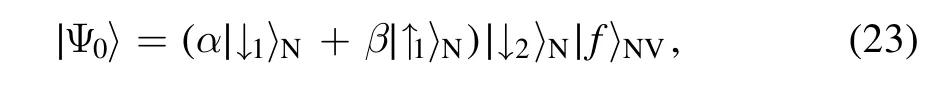
where α,β∊C,and|α|2+|β|2=1.According to quantum dynamics above,after an interaction timet=π/Ω,the final system state becomes

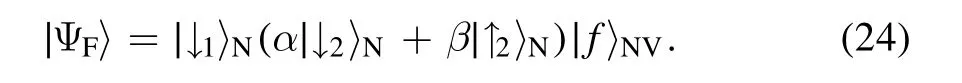
The quantum information in nuclear spin 1 is transferred to nuclear spin 2.

To gain insight into the origin of this QST,we begin to consider a subset of Hilbert subspaces of the system(see figure 1(b)).A dipole–dipole interaction causes a splitting of the system energy,with the corresponding energy eigenvalues,respectively.Then the total Hilbert space is split into three corresponding invariant subspaces

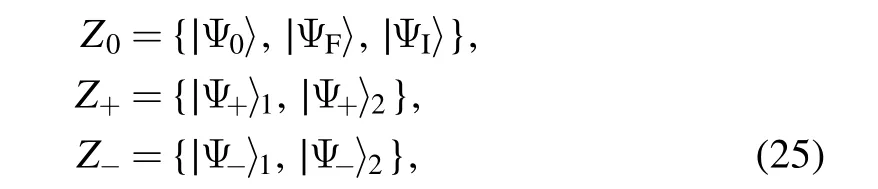
where

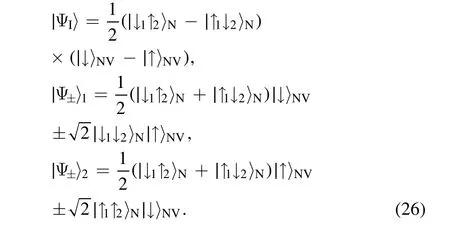
Large splitting of energy levels results in the difficulty of the transitions between different energy levels.However,the states that belong to the same energy level interact with each other easily.If the initial state lies in the invariant subspaceZ0,the survival probability inZ0remains unity.A field drives the state transition from∣ψ0〉to|ΨI〉,and then from|ΨI〉to∣ψF〉.Mediated by the NV center,the quantum state is transferred between two distant nuclear spins,

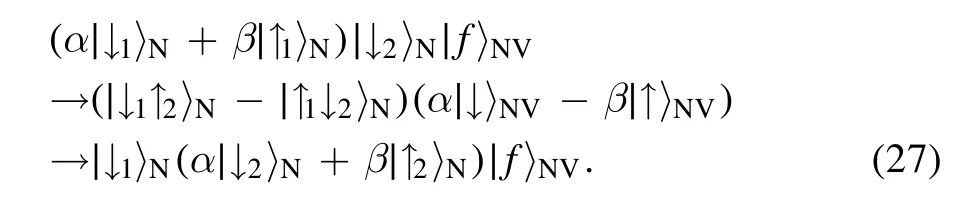
This process can be generalized to perform QST between any pair of multiple nuclear spins.

Now,we investigate the effect of systematic errors,which are caused by fixed fluctuations in the system parameters.For example,the fluctuation of driving-field Rabi frequency Ω can be assumed as a fixed valueδΩ = Ω′ −Ω with Ω′ being the real value in the experiment.HDDin equation(3)describes the dipole–dipole interaction between the NV center spin and nuclear spins.A small uncertainty or variation in the separationrleads to a corresponding change ing.A small fluctuation of the interaction timetalso affects QST.Thus,we consider three factors during the process of QST.Figure 5 shows that small fluctuations ofg,Ω andthave little impact on the fidelity of QST,on the condition that Ω ≪g.Even in a large fluctuation(δg/g=0.1,δt/t=0.1),the fidelity remains high(≥0.98).The results of numerical simulation in fact demonstrate that QST between a nuclearspin pair is robust against variations and uncertainty in the distance between the NV center and nuclear spins.

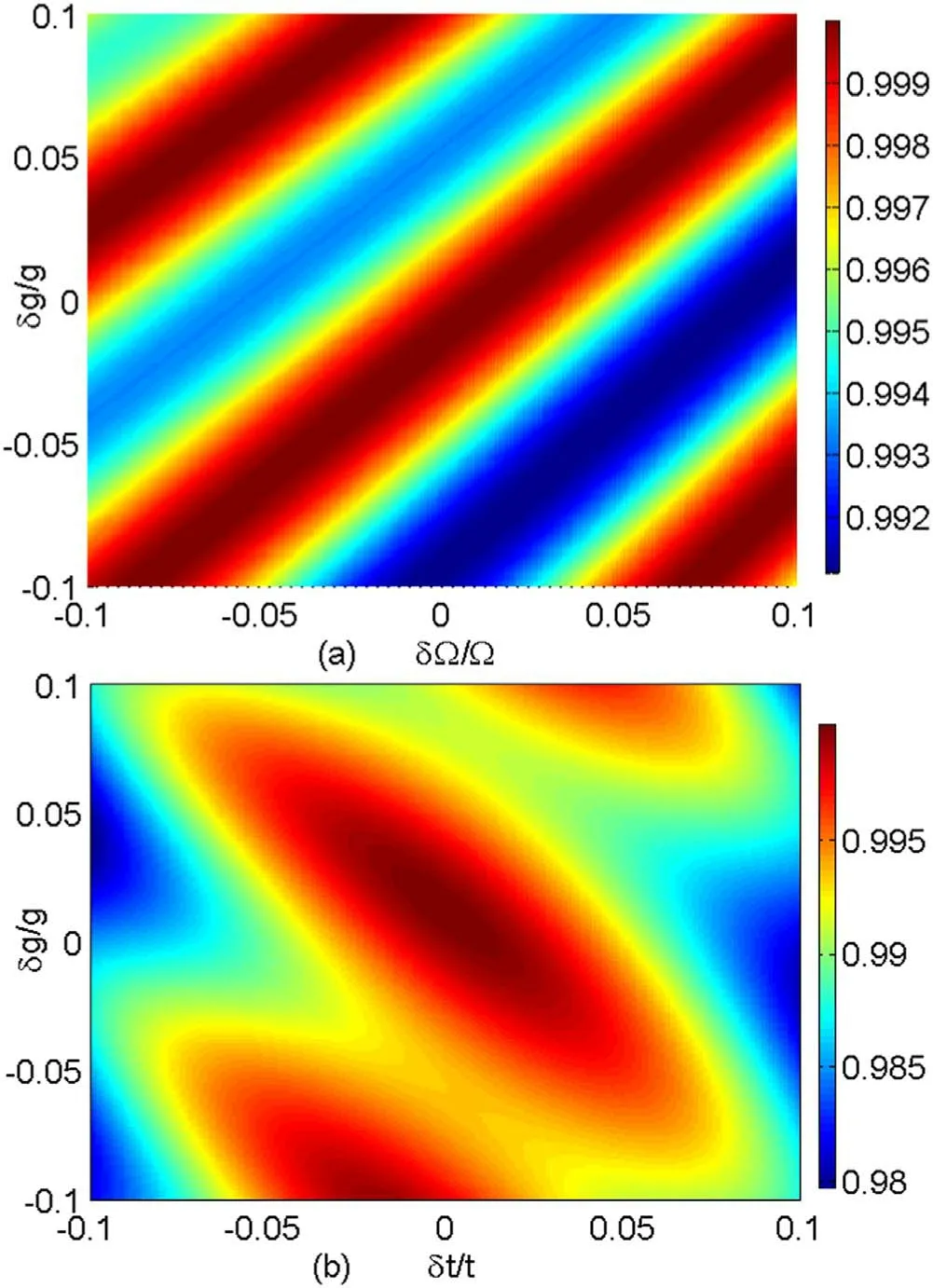
Figure 5.(Color online)The fluctuation of the interaction time,the coupling strength,and the Rabi frequency of the driving field influence the fidelity of QST,considering no spontaneous decay,for the original g∼2π×2 MHz and Ω∼2π×210 kHz.(a)The fidelity of QST versus δg/g and δΩ/Ω.(b)The fidelity of QST versus δg/g and δt/t with the original interaction time T=π/Ω.

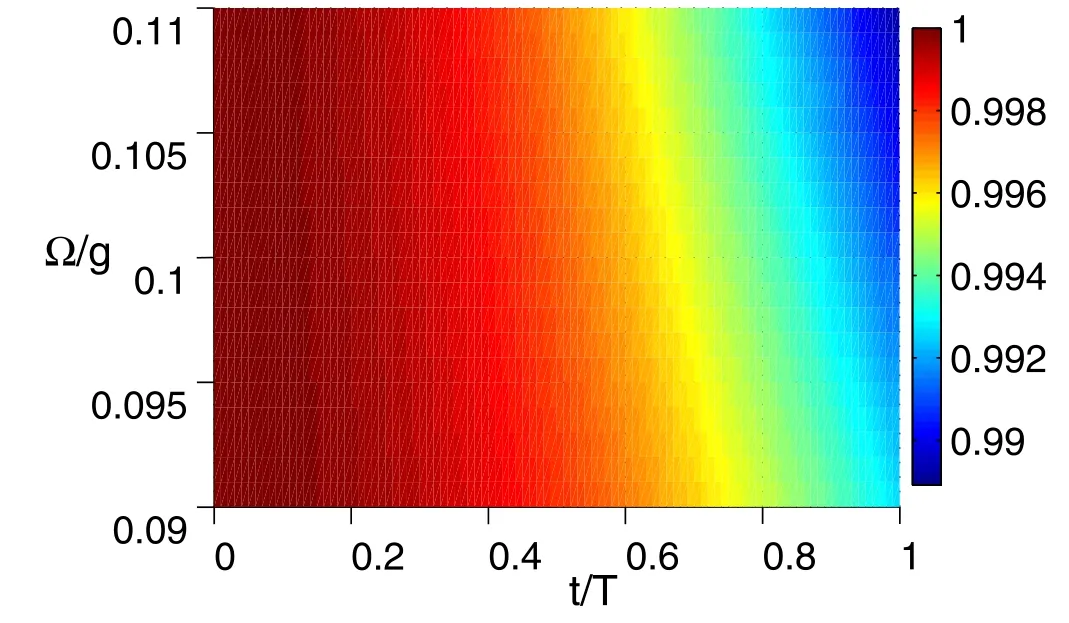
Figure 6.(Color online)The survival probability in ground state|0〉NV of NV center P0(t)versus the scaled time t/T and Ω/g,with g∼2π×2 MHz and the interaction time T=π/Ω.

Figure 7.(Color online)The off-resonant coupling and the spontaneous decay of NV center and nuclear spin influence the fidelity of QST with g∼2π×2 MHz and Ω∼2π×210 kHz,for t=π/Ω.(a)The fidelity of QST versus γN/g and Δ/g.(b)The fidelity of QST versus γNV/g and Δ/g.

Considering the hybrid quantum devices based on NV centers in a diamond,the dominant decoherence mechanism is photon emission via exciton decays of the NV center.If the system is initially in the state|f〉NV=|ms=+1〉,the survival probability reads

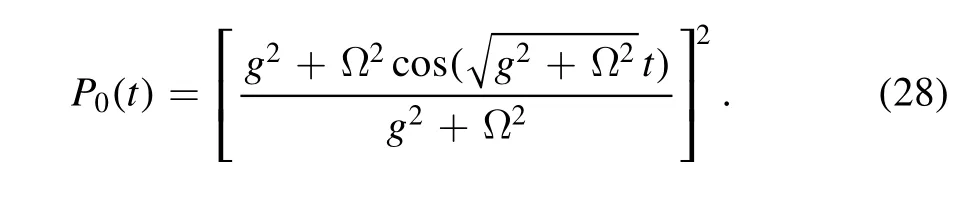
As shown in figure 6,in regimeg≫Ω,the survival probability in ground state|f〉is about 1.In our scheme,ΔE≫Ω,the weakly driving field ensures the NV center stays in the state|ms=+1〉NV,which belongs to the zero energy subspace.The probability in the excited state is so small that the photon emission is suppressed.

Now,numerical simulations are used to show influences of spontaneous decay and off-resonant coupling.As shown in figure 7,when the spontaneous decay rate of NV center γNV/g≥0.01,with the scaled off-resonant strength Δ/g=0.01,the fidelityF≥0.94.However,the fidelityF≥0.97,when the spontaneous decay rate of nuclear spin γN/g≥0.01.Thus,under the condition that ΔE≫Ω,small off-resonant couplings and small decay rate of the NV center have little impact on the fidelity of QST.

4.Experimental feasibility discussion

In this section,we explain the experimental realization of our model and present further applications.We first discuss how to prepare and manipulate the system spin states.Linearly polarized optical excitation preferentially pumps the NV center spin into ground state|ms=0〉NV.The laser is then turned off and a magnetic adiabatic passage through the|ms=0〉NV→|ms=+1〉NVresonance robustly transfers the initialized spin population into the state|ms=+1〉NV[18],which is the initial NV center spin state we need.Then,let magnetic-dipole coupling and mechanically driving take effect.A stress wave is turned on at a frequency ωHBARcorresponding to a resonance of the HBAR.The mechanical spin resonance|ms=+1〉NV→|ms=−1〉NVspin transition can be detected via optical pulses.

From the simulations above we can see that the fidelity of the scheme is spoiled by dephasing.Therefore,implementing this proposal with high fidelity requires that the dephasing rate γNV,γN≪g.The relaxation timeT1of an NV center can be achieved the order of seconds at low temperature around 4 K[34].The decoherence timeT2can be prolonged to 15μs using a continuous dynamical decoupling of an NV center spin with a mechanical resonator[35].In addition,in a high purity diamond,T2of a single NV center is longer than 600μs at room temperature[36].Nuclear spins have long relaxation and coherence time in comparison with those of electron spins in a diamond.The relaxation time of single nuclear spinT1=(75±20)μs at room temperature[37].The operating time required of entangling gates or QST ist=π/Ω ≈2.5μs,which is far less thanT1andT2of the NV center(or nuclear spins).Therefore reasonable values of fidelity in our scheme can be anticipated.

Normally,driving NV electron spins independently of the nuclear spins is not easy.In our scheme,mechanical spin control of an NV center and magnetic-dipolar coupling of nuclear-NV spins is a good alternative.However,there are also some challenges in experimental realization of our model.It is challenging to individually address one of the nuclear spins without affecting the other,no matter whether two nuclear spins have similar couplings to the NV center or not.

Our scheme can be extended to multi-qubit systems.An NV center spin is placed at the center of a polygon geometry with each vertex occupied by a nuclear spin.Based on our scheme,any two nuclear spins indirectly interact.By considering the polygon geometry a basic unit,a manybody location can be achieved mediated by the interactions between distant NV centers[38].Furthermore,it may be used for simulating spin models with topological order[39].

5.Summary

In summary,based on a weak driving field and dipole–dipole coupling,we present a protocol for the generation of entangling gates and quantum-state transfer between two separated nuclear spins mediated by an NV center in a diamond.The system coherently evolves within the quantum dark subspaces.The results of numerical simulations show that our protocol is robust against the fluctuations of external fields and the uncertainty of the distance between the NV center and nuclear spins.This scheme can also be applied in a biological probe.Nuclear spins in a single molecule were studied to understand structural information in chemical and biological processes[40].Through dipole coupling to nuclear spins,an NV center can effectively act as a dipole ‘antenna’,detecting spins at different spatial locations.For example,NV centers can be used to detect the charge recombination rate in a radical pair reaction[41].

Acknowledgments

The authors acknowledge J P Hadden and H-Z Wu for helpful discussions and suggestions.This work is supported by the National Natural Science Foundation of China under Grant No.11405031 and No.11875108,the National Natural Science Foundation of Fujian Province China under Grant No.2019J01219.