Coherent control of spin tunneling in a driven spin–orbit coupled bosonic triple well

Yuxin Luo,Jia Yi,Wenjuan Li,Xin Xie,Yunrong Luo and Wenhua Hai

1 Key Laboratory for Matter Microstructure and Function of Hunan Province,and Key Laboratory of Lowdimensional Quantum Structures and Quantum Control of Ministry of Education,School of Physics and Electronics,Hunan Normal University,Changsha 410081,China

2 School of Management,Hunan University of Information Technology,Changsha 410151,China

Abstract We investigate the coherent control of spin tunneling for a spin–orbit(SO)coupled boson trapped in a driven triple well.In the high-frequency limit,the quasienergies of the system are obtained analytically and the fine energy band structures are shown.By regulating the driving parameters,we reveal that the directed spin-flipping or spin-conserving tunneling of an SOcoupled boson occurs along different pathways and in different directions.The analytical results are demonstrated by numerical simulations and good agreements are found.Further,an interesting scheme of quantum spin tunneling switch with or without spin-flipping is presented.The results may have potential applications in the design of spintronic devices.

Keywords:coherent control,spin tunneling,spin–orbit coupling,triple well

1.Introduction

Spin–orbit(SO)coupling is the interaction between spin and motion of a particle,which plays a crucial role in many important physical phenomena,e.g.spin-Hall effect[1],topological insulator[2],and the persistent spin helix[3].For ultracold atoms,SO coupling can be created by utilizing the interaction between laser and atom,which yields Abelian or non-Abelian gauge fields for ultracold atoms in the dressed two hyperfine atomic internal states.As is well-known,the electrons are fermions in the material,but ultracold atoms may be bosons.Therefore,SO-coupled ultracold bosonic gases will lead to novel SO physics that has not been explored in solid materials.

Recently,SO coupling of ultracold atomic gases has been realized in experiments[4–9],which provides a brand new platform to investigate SO coupling physics,due to the unprecedented tunability of experimental parameters.A number of research works have focused on the interesting dynamics of SO-coupled ultracold atoms,for instance,quantum dynamics of SO-coupled Bose–Einstein condensates(BECs)in a double well[10–13],coherent control of an SOcoupled atom in a double-well potential[14],controlling stable spin tunneling in a non-Hermitian double-well system[15],Anderson localization of SO-coupled ultracold atomic gases in an optical lattice[16],Macroscopic Klein tunneling in SO-coupled BECs[17],Landau–Zener transition in an SOcoupled BEC[18],spin dynamics of SO-coupled BECs[19],nonequilibrium dynamics of two-component bosons in an optical lattice[20],controlling localization and directed motion of an SO-coupled single atom in a bipartite lattice[21],Bloch oscillation dynamics of an SO-coupled ultracold atomic gas in an optical lattice[22],quantum tunneling of an SO-coupled ultracold atom in an optical lattice with an impurity[23],controlling second-order tunneling of an SOcoupled atom in optical lattices[24],and so on.

As mentioned above,many works focus on the tunneling dynamical properties of SO-coupled ultracold atomic gases held in a double well or an optical lattice.To the best of our knowledge,the coherent control of spin tunneling for SOcoupled ultracold atoms confined in a triple well is rarely investigated.However,the triple-well model is an important one to study the coherent control of spin tunneling and is a bridge between the double-well and optical lattice models for a better understanding of the spin tunneling dynamics of SOcoupled ultracold atoms in the quantum wells.Thus,it motivates us to investigate the quantum spin tunneling in an SO-coupled bosonic triple-well system.

In this paper,we theoretically study the coherent control of spin tunneling for an SO-coupled boson confined in a driven triple well.In the high-frequency limit,the quasienergies of the SO-coupled ultracold atomic triple-well system are analytically obtained and the quasienergy spectra are shown.By adjusting the strength of the time-dependent driving field,we can manipulate the directed spin-flipping or spin-conserving tunneling of an SO-coupled boson along different pathways and in different directions.Further,we present an intriguing scheme of a quantum spin switch for transporting an SO-coupled boson accompanied with or without spin-flipping from well 1 to well 3.These results may be useful for the design of spintronic devices[25].

2.Analytical solutions and quasienergy spectra in the high-frequency limit

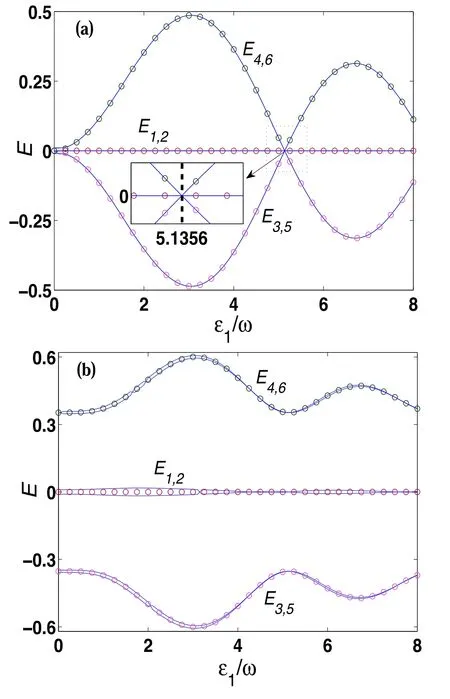
Figure 1.Quasienergy as a function of the driving parameter ε1/ω for γ=0.5,ν=1,ω=50,Ω=100,and(a)ε2=5.1356ω;(b)ε2=2ω.Here,circles denote the analytical results and solid curves label the numerical correspondences.Hereafter,any parameter adopted in the figures is dimensionless.

Figure 2.Time evolutions of the probabilities Pk(t)for the initial conditions P3(0)=1 and Pk(0)=0(k ≠3),and the system parameters γ=0.5,ν=1,ω=50,Ω=100,and(a)ε1=2ω,ε2=5.1356ω;(b)ε1=ε2=5.1356ω;(c)ε1=5.1356ω,ε2=2ω.Dashed lines denote the analytical results and solid curves label the numerical correspondences.

3.Directed tunneling and spin switch with or without spin-flipping

Coherent manipulation of quantum tunneling is an interesting research subject in quantum information technologies[39,40].Generally,quantum tunneling of ultracold atomic systems relies intensively on the periodic driving external field.Thus,the quantum spin tunneling and transport of an SO-coupled ultracold boson held in a triple well can be manipulated by adjusting the driving parameters.In the section,we will focus on studying the directed tunneling and spin tunneling switch with or without spin-flipping.

3.1.Directed tunneling with or without spin-flipping

For an SO-coupled ultracold atomic triple-well system,an attractive physical problem is how to control the directed spin-flipping or spin-conserving tunneling of an SO-coupled atom from the initial middle well to the left well or to the right well.Based on equation(5),it can be seen that when the SOcoupling strength γ is half integer or integer,quantum tunneling with or without spin-flipping can occur.Here,we will try to manipulate the directed spin-flipping tunneling of a spin-up boson initially located in the well 2 as an example.In order to realize the directed spin-flipping tunneling of the spin-up particle from well 2 to well 1,it is easily found from equation(5)that when the effective coupling constants satisfyJ1=J4=J5=0 andJ3≠0,b3is only coupled withb2.It means that the SCDT occurs.We take the parameters γ=0.5,ν=1,ω=50,Ω=100,ε1=2ω,ε2=5.1356ω satisfying the conditionsJ1=J4=J5=0 andJ3≠0 to plot the time evolutions of the probabilities in figure 2(a).Clearly,the spinflipping tunneling channel between well 2 and well 3 is closed and the particle performs a Rabi oscillation of spin-flipping along this pathway between well 2 and well 1,namely,the directed spin-flipping tunneling takes place between initial state|0,↑,0〉and state|↓,0,0〉with tunneling time Δt≈4.4.It means the occurrence of SCDT and the set of parameters corresponds to the degeneracy position of the partial quasienergies in figure 1(a).If we set the same parameters as in figure 2(a)except for ε1=5.1356ω,which corresponds to the collapse(crossing)point of all the quasienergies in figure 1(a),the quantum tunneling of the particle will be frozen.It means the CDT occurs as shown in figure 2(b).

Further,from equation(5)it can also be found when the effective coupling constants satisfyJ1=J3=J4=0 andJ5≠0,the probability functionb3is only related to functionb6,which means the SCDT happens.We fix the same initial conditions and parameters as that in figure 2(a)except for ε1=5.1356ω and ε2=2ω to plot the time evolutions of the probabilities in figure 2(c).Clearly,the directed spin-flipping tunneling along another pathway between well 2 and well 3 occurs,in which the spin particle performs a spin-flipping Rabi oscillation between state|0,↑,0〉and state|0,0,↓〉with tunneling time Δt≈4.4.It means the SCDT occurs and the set of parameters corresponds to the degeneracy location of the partial quasienergies in figure 1(b).The analytical results(dashed lines)based on equation(5)are in perfect agreement with the numerical results from the accurate model(3)in figure 2.Because the above-mentioned results are related to controlling the directed spin-flipping tunneling of a spin boson,it is similar to the case of manipulating the directed spin-conserving tunneling of the particle.

3.2.Quantum spin tunneling switch with or without spin-flipping

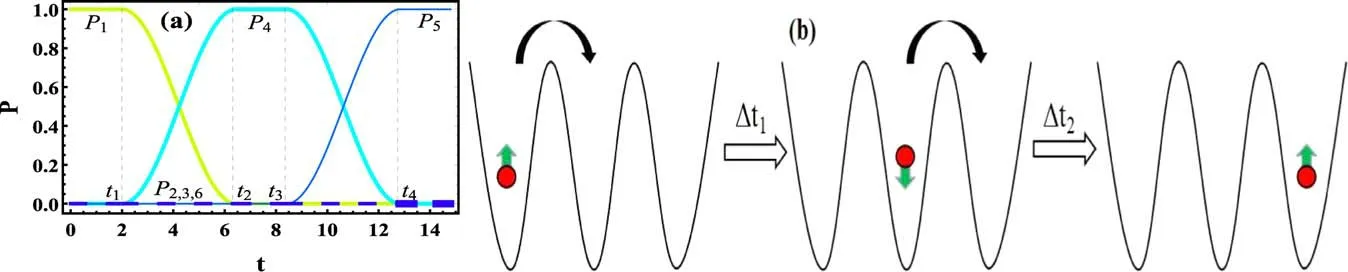
Figure 3.(a)Time evolutions of the probabilities Pk(t)for the initial conditions P1(0)=1 and Pk(0)=0(k ≠1),and the system parameters γ=0.5,ν=1,ω=50,Ω=100,and ε1=ε2=5.1356ω in intervals 0 ≤t

From the above subsection,we find the time-dependent driving field affects dramatically spin tunneling dynamics of this system,thus we can propose a scheme of quantum spin tunneling switch with or without spin-flipping by means of sudden regulating of driving parameters to control the occurrence and suppression of quantum tunneling.The means have been performed in many research works[41–44].Here,we present a scheme of quantum spin tunneling switch with spin-flipping by adjusting the driving strength as an example,as shown in figure 3.In figure 3(a),we take a spin-up boson initially occupied in well 1 and set the parameters γ=0.5,ν=1,ω=50,Ω=100,ε1=ε2=5.1356ω corresponding to the collapse(crossing)point of all the quasienergies in figure 1(a).One can see that the spin-up boson is frozen in well 1,due to the CDT effect.At any given timet=t1=2,the driving strength ε1is changed to ε1=2ω and holds this value until the time ist=t2=6.4.At the moment,the spin-up particle tunnels completely from state|↑,0,0〉to state|0,↓,0〉.Then we immediately adjust the driving strength ε1to ε1=5.1356ω,such that the state|0,↓,0〉is kept which is attributed to the effect of CDT.At any given timet=t3=8.4,we regulate the driving strength ε2to ε2=2ω and preserve this value untilt=t4=12.8.At this time,the spin-down particle tunnels completely from state|0,↓,0〉to state|0,0,↑〉.Then,we return the driving strength ε2to ε2=5.1356ω,so that the final state|0,0,↑〉is kept,due to the CDT effect.Therefore,the spin-up boson is successfully transported through two spin-flipping tunnels from well 1 to well 3 by adjusting the driving strength εi(i=1,2)of the driving external fields,namely,the quantum spin tunneling switch with spin-flipping is theoretically realized.From figure 3(a),it is also found that we can manipulate the spinflipping tunneling of the spin particle from an arbitrarily initial occupied well to any other well.The corresponding spatial distributions of the spin particle at the tuning moments are shown in figure 3(b),where Δtidenotes transferring time between the different populations and the transferring time Δt1=Δt2=t2−t1=t4−t3=4.4.Similarly,the quantum spin tunneling switch without spin-flipping can also be performed by adjusting the driving parameters.

4.Conclusion and discussion

In conclusion,we have investigated the coherent control of spin tunneling for an SO-coupled boson trapped in a driven triple well.In the high-frequency limit,we analytically obtain the Floquet quasienergies of the system and the fine quasienergy spectra are shown.By modulating the strength of the driving external field,we can control the directed spin-flipping or spin-conserving tunneling of an SO-coupled boson along different pathways and in different directions from the middle well to the left well or to the right well.The analytical results are demonstrated by numerical calculations and perfect agreements between both are shown.Further,based on the combined effect of CDT and SCDT,we propose a diverting scheme of quantum spin tunneling switch in which a spin particle is transported with or without spin-flipping from the initial well 1 to the final well 3.It is worth noting that we also can manipulate the spin-flipping or spin-conversing tunneling of a spin boson from an arbitrarily initial occupied well to any other well.These results may be useful in the design of spintronic devices and quantum information technology.

Acknowledgments

This work was supported by the Scientific Research Foundation of Hunan Provincial Education Department under Grants No.21B0063 and No.18C0027,the Hunan Provincial Natural Science Foundation of China under Grants No.2021JJ30435 and No.2017JJ3208,and the National Natural Science Foundation of China under Grant No.11747034.