主余震作用下顶底角钢自复位梁柱节点的抗震性能研究

俞昊然， 李维滨， 郎泰申， 郑 鑫

(1.东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京 211189； 2.东南大学 土木工程学院，南京 211189)

为使结构能够在一定强度的地震作用下快速恢复预定的使用功能，研究者们提出了结构抗震设计的新概念——可恢复功能抗震结构[1]。可恢复功能抗震结构是指应用自复位、摇摆、可更换或附加耗能装置等技术，在遭受设防或罕遇水准的地震作用时，能够保持可接受的功能且震后不需修复或稍加修复即可恢复其使用功能的结构[2]。

自复位钢框架梁柱节点属于典型的可恢复功能抗震结构。20世纪末，自复位钢框架梁柱节点的概念由Garlock等[3-5]首先提出，节点形式如图1所示。节点的梁、柱翼缘通过顶底角钢和螺栓进行连接，预应力钢绞线沿梁长贯穿，并在柱的外侧翼缘进行锚固，通过对钢绞线施加预应力使得节点拥有足够的抗弯能力，并且在梁柱接触面间产生摩擦力，该摩擦力与顶底角钢共同承担竖向剪力。试验研究发现[4-5]，该梁柱节点在遭受地震作用时能够通过预应力钢绞线实现自动复位，且节点转动时顶底角发生塑性变形可耗散地震输入的能量。由于震后梁、柱等主体构件不发生破坏，且受损的角钢可拆卸、更换，这使得结构具备了损伤可控性和可修复性。基于钢绞线提供自复位驱动力的原理，学者们随后将研究重心集中到自复位节点耗能机制的设计研发上，分别提出了耗能软钢筋[6]、梁端翼缘板摩擦[7-10]、梁端腹板摩擦[11]等耗能形式。近年来，国内许多学者结合工程实践对自复位钢框架梁柱节点不断改进创新，如针对高层建筑提出了自复位装配式钢框架梁柱节点[12-14]，基于常规PEC柱节点改进形成了卷边PEC柱-钢梁自复位摩擦耗能型节点[15]等。

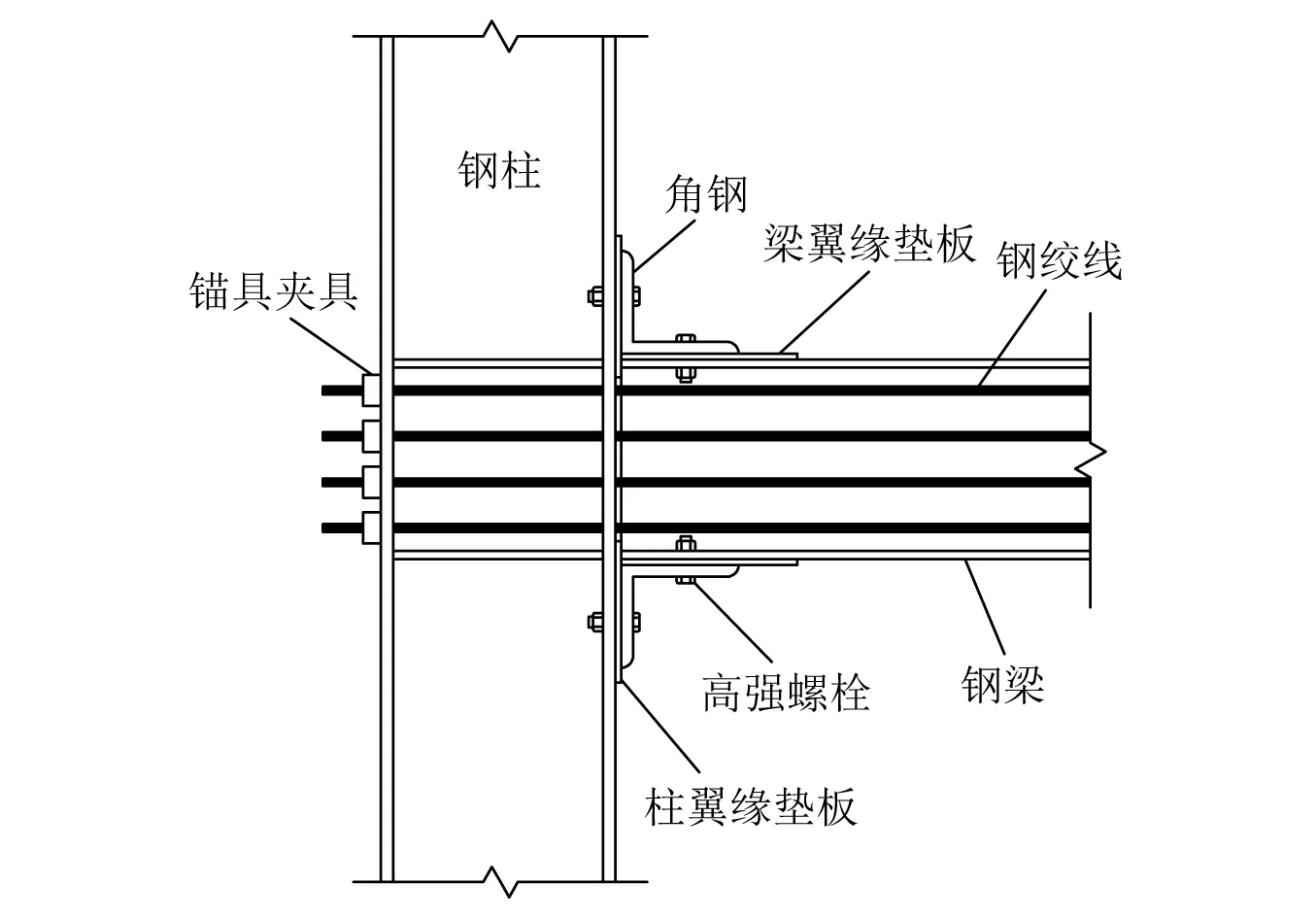
图1 Ricles和Garlock等提出的顶底角钢自复位梁柱节点Fig.1 Self-centering beam-to-column connection with top-and-seat angles proposed by Ricles and Garlock, et al

目前，对于自复位梁柱节点抗震性能的研究大多是在单次地震或单次加载的工况下进行的。然而，一次主震发生后时常还会伴随多次余震的出现，余震会对建筑物造成进一步的破坏，甚至会成为导致结构倒塌的决定性因素，因此余震对结构造成的影响同样不可忽略。自复位梁柱节点虽然具有震后残余变形小，主体结构可免遭破坏，结构易于修复等特征，但是由主余震组合而成的地震序列一般较为密集且间隔时间短，节点中的耗能构件受到损伤后很难及时对其进行修复或更换，从而在余震作用下损伤会进一步累积，结构的抗震能力将受到影响，并且钢绞线中预拉力的损失也会造成节点的刚度、承载力下降，因此研究自复位梁柱节点在主余震共同作用下的抗震性能具有重要的实践意义。本文以顶底角钢形式的自复位钢框架梁柱节点为研究对象，采用试验和有限元模拟方法，通过对节点进行连续的拟静力试验加载以研究主余震作用对其抗震性能的影响。

1 试验概况

1.1 试件设计

设计了1个足尺T形自复位梁柱节点试件，节点形式采用Garlock等提出的顶底角钢自复位节点。试件由钢柱、钢梁、钢绞线、角钢、高强螺栓等构成，构件几何尺寸如图2所示。钢梁采用热轧H型钢HM340×250×9×14，钢柱采用热轧H型钢HW400×400×13×21，梁、柱长度分别为2.0 m与2.8 m。顶底角钢采用型号为∟200×20的等肢角钢，在与角钢接触的梁、柱翼缘表面分别焊接10 mm厚的垫板，连接角钢的螺栓采用强度为10.9级的M20高强螺栓。试件由4根1×7Ф15.2的钢绞线为节点提供自复位回复力，每根钢绞线的设计预拉力为80 kN，沿梁长方向通长布置，并采用单孔夹片锚具进行锚固，钢绞线安装时一端锚固于柱外侧翼缘，另一端锚固于梁端板。

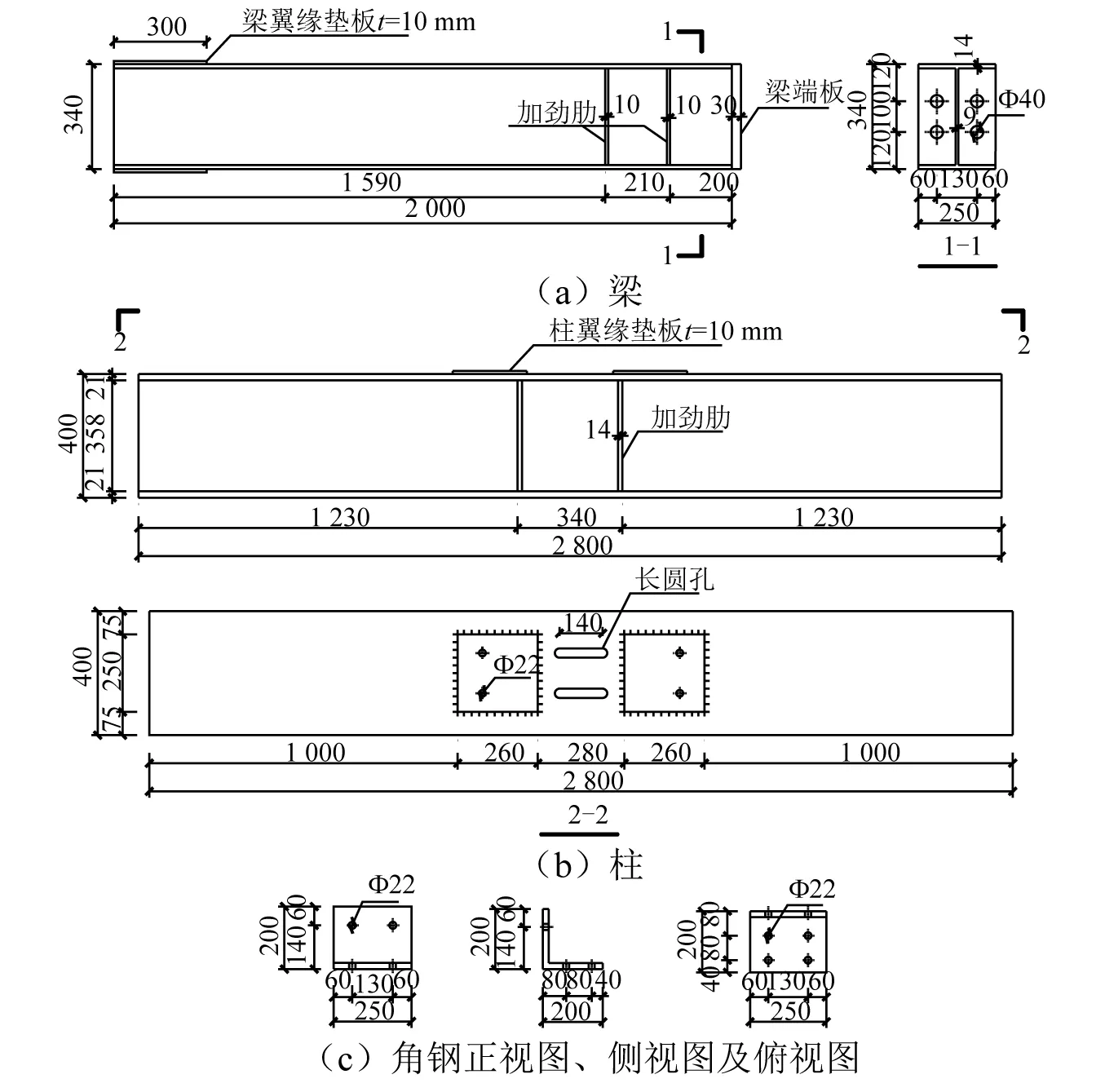
图2 构件尺寸Fig.2 Geometric dimensions of components

1.2 材料力学性能

试件中梁、柱、角钢均采用Q235B钢材制成，钢绞线的公称抗拉强度为1 860 MPa。分别对各构件进行材料取样，通过液压万能试验机进行材性拉伸试验，测试结果如表1所示。

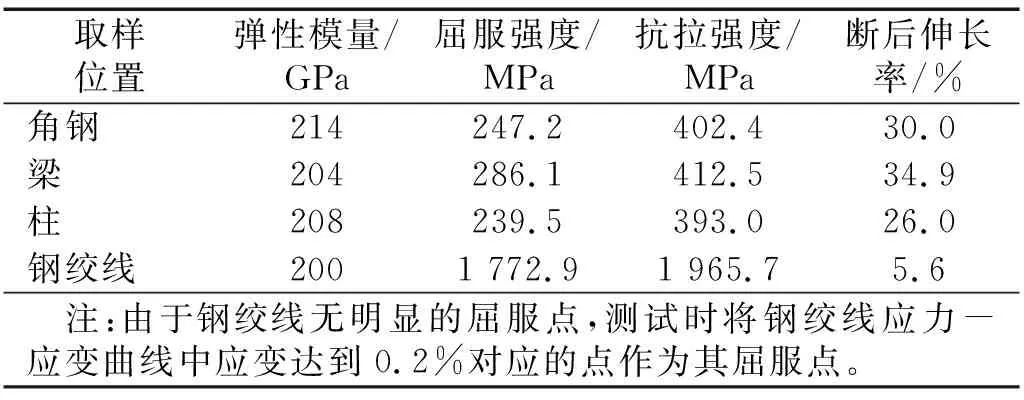
表1 材性试验结果Tab.1 Results of tensile coupon test

1.3 加载装置与测点布置

试验装置与加载仪器如图3所示。试件中钢柱平行于地面布置并在两端进行固定，其在水平方向上使用千斤顶和压梁顶紧，竖直方向采用锚杆与压板压住，锚杆固定在地锚孔内。采用伺服作动器对节点的梁端施加低周循环荷载，伺服作动器一端固定于反力墙，另一端通过加载板和锚杆与梁端连接，使得作动器与梁端能够均匀传力和同步位移。在钢梁加载点下部设置侧向支撑，以防止钢梁在试验过程中产生平面外扭转。

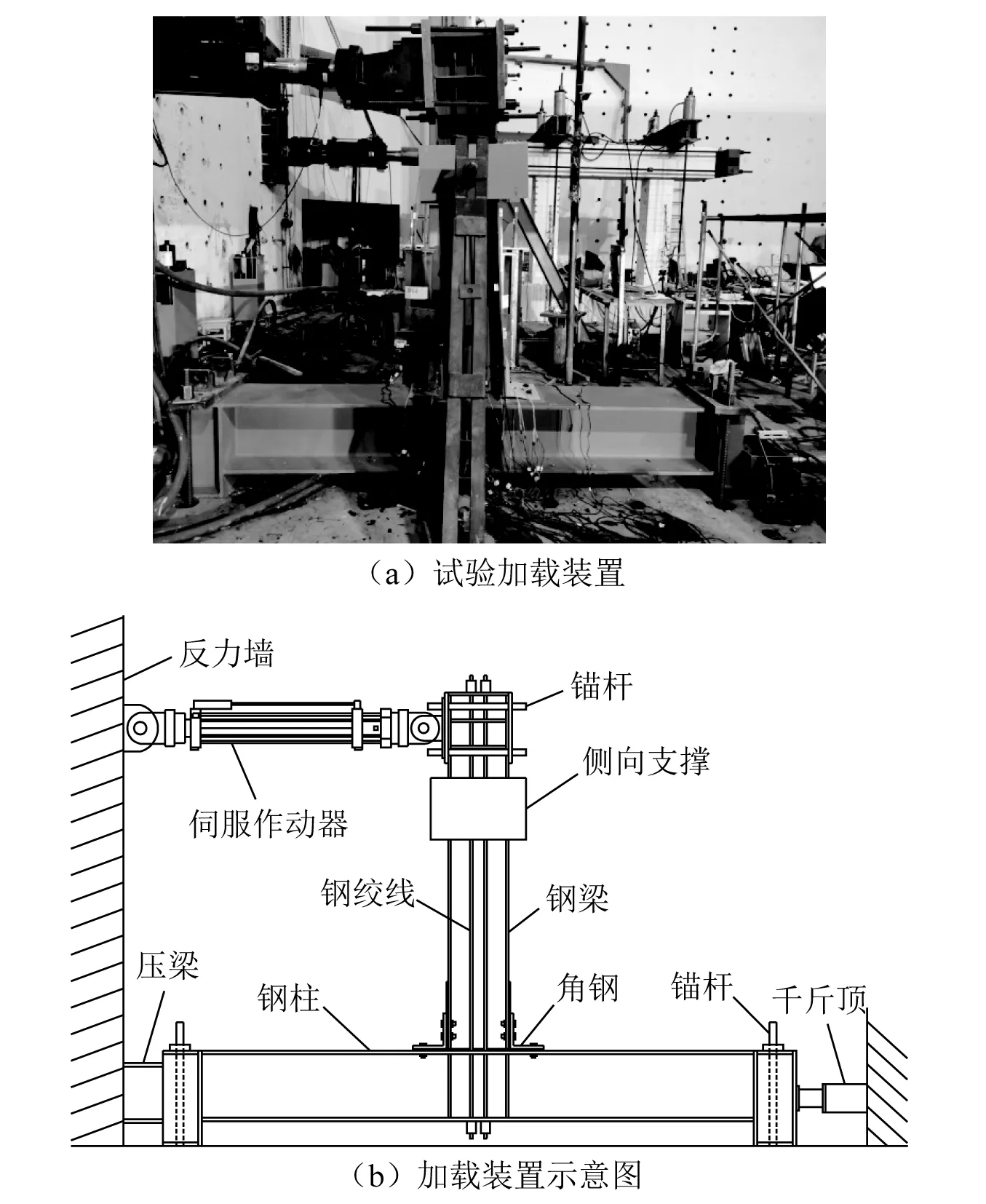
图3 加载装置Fig.3 Test set-up

在柱端设置顶杆式位移计，测量加载过程中试件产生的微小平动，通过计算消除系统误差。在角钢及钢梁顶端、底部设置位移计，分别测量试验中角钢从柱面脱开的距离以及钢梁顶端和底部的水平位移。分别于角钢两肢及节点核心区的梁柱翼缘、腹板粘贴应变片，测量试验过程中构件的应力应变情况。在钢梁顶部的钢绞线端头安装穿心式压力传感器，以测量钢绞线在加载过程中的拉力变化。

1.4 加载制度

拟静力试验是通过施加低周循环荷载来考察结构在地震作用下的响应，而改变加载峰值的顺序、大小、次数可考察结构在不同形式地震作用下的力学性能[16-17]。本试验通过具有两次峰值的拟静力加载来模拟主余震对节点的作用，即节点先经历一个逐级增大的循环荷载作用，将此第一阶段(S1)的加载视为主震；第一阶段加载后，对节点再次施加循环荷载，此时该第二阶段(S2)的循环荷载可以视为余震。试验采用梁端位移控制的加载模式，每个阶段的加载位移幅值根据美国AISC 341-05[18]的要求进行设置，主余震的强度可通过加载的位移荷载幅值大小体现。为便于比较分析，研究时设定两阶段加载中位移荷载幅值、步幅和循环次数均相同。以最大层间位移角为3%rad的两阶段加载为例进行加载制度的说明，其加载历程如图4所示。每个阶段中加载的层间位移角幅值逐级递增，分别为0.375%rad，0.5%rad，0.75%rad，1%rad，1.5%rad，2%rad，3%rad，每级荷载循环两次，前后两阶段施加的位移荷载相同。

图4 最大层间位移角为3%rad时的加载历程Fig.4 Loading protocol with a maximum inter-storey drift ratio of 3%rad

一般情况下自复位钢框架结构在地震作用下的层间变形大于普通抗弯钢框架，因此试验加载中选取了较大的位移峰值范围。试件共经历5次完整的循环荷载加载，其最大层间位移角按顺序依次为1%rad，2%rad，3%rad，4%rad，5%rad，以探究不同强度的主余震作用对自复位节点抗震性能的影响。

1.5 试件修复

自复位钢框架梁柱节点作为可恢复功能的抗震结构，具有良好的损伤可控性和可修复性，地震作用后梁柱等主体构件处于弹性状态，塑形变形主要集中于起耗能作用的角钢上，因此试验中每经过一次完整的加载需要更换一组新的角钢。由于加载过程中角钢与梁柱翼缘垫板之间会产生挤压磨损，在安装一组新的角钢前，需要使用角磨机将垫板接触面打磨平整。试验中螺栓孔没有产生明显的塑性变形，因此无需进行扩孔或打磨处理。角钢更换完成后，还需要对钢绞线依次进行补张拉，使其恢复到初始预拉力水平。

2 试验结果及分析

2.1 试验现象

第1次加载中，当位移荷载接近1%rad时试件的角钢柱肢微微抬起，其余时刻角钢与翼缘垫板贴合紧密，加载结束后角钢未出现肉眼可见的塑性变形。第2次加载中，随着位移荷载幅值逐渐增大，角钢与柱翼缘垫板之间的脱开间隙也越来越明显，图5(a)为位移荷载达到2%rad时脱开的角钢，两个阶段中角钢柱肢的最大脱开距离分别为6.6 mm(S1)和6.7 mm(S2)，加载结束后角钢柱肢的边侧出现轻微的翘曲变形。第3次加载中，角钢与柱翼缘垫板的脱开距离明显增加，在两阶段最大脱开距离分别为12.6 mm(S1)和13.1 mm(S2)，且第一阶段加载结束后角钢柱肢边侧出现翘曲变形(如图5(b))，最大变形值为3.4 mm，第二阶段加载结束后该处翘曲变形略微增大，最大变形值为4.1 mm，同时角钢柱肢螺栓孔附近的漆面开始起皮和脱落，梁肢也出现轻微的塑性变形。第4次加载中，角钢与柱翼缘垫板的最大脱开距离分别为15.0 mm(S1)和17.1 mm(S2)，两阶段的变形差值相比于前3次加载明显增大，这表明了该次加载中第一阶段产生了较大的初始损伤和残余变形，进而导致在第二阶段加载时角钢柱肢脱开变形的刚度明显降低。两阶段角钢柱肢的翘曲残余变形最大值分别为4.4 mm(S1)和5.0 mm(S2)，且加载结束后柱肢螺栓孔附近的漆面剥落明显，开始出现大面积的鳞片状起皮现象，角钢表面磨损破坏严重(如图5(c))。第5次加载中，角钢与柱翼缘垫板的最大脱开距离分别为19.9 mm(S1)和21.9 mm(S2)，加载结束后角钢柱肢的翘曲残余变形达到5.8 mm(S1)和6.4 mm(S2)，将损坏的角钢拆下，可观察到其塑性变形已十分明显，如图5(d)所示。

根据应变采集数据，在整个试验过程中梁、柱核心区的翼缘、腹板应力水平较低处于弹性阶段，而塑性变形均出现于角钢中，这说明顶底角钢自复位梁柱节点在主余震作用下依然具有损伤可控性。角钢随着位移荷载的增大其塑性发展越加充分，且由于第一阶段加载中角钢出现了不同程度的残余变形和损伤，其在第二阶段加载时应力水平也相应提高。

图5 试验中角钢的主要特征Fig.5 Main characteristics of the angle steels in the test

2.2 滞回曲线

试件的滞回曲线如图6所示。随着加载次序的递进，试件所经历的最大层间位移角由1%rad至5%rad逐步增大，滞回曲线变得更加饱满。在前两次加载中，试件的滞回曲线于中部捏缩，能够较好地聚焦于坐标原点，这展现了节点良好的自复位性能；后3次加载中，试件的残余变形逐渐增大，不过相对前两次加载其滞回曲线更为饱满，耗能更加充分。从第2次加载开始，两个阶段中滞回曲线的形状区别变得明显，具体表现为第2阶段的曲线包络于第1阶段曲线中，形状相对扁平，曲线包络面积与总体弯距水平均小于第1阶段。由此可知，相比于单独主震作用的情况，主余震作用下的顶底角钢自复位梁柱节点其滞回性能有所降低，且当主震强度较大时其所受影响更为明显。

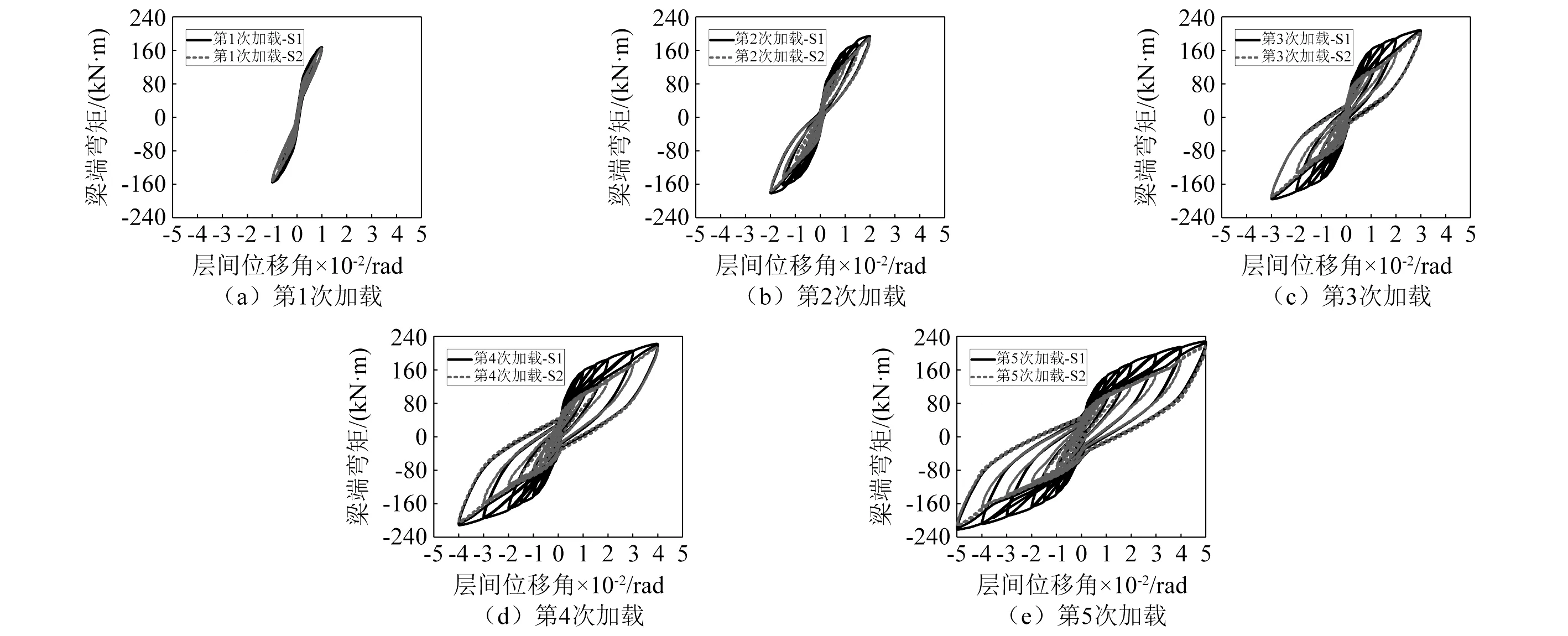
图6 滞回曲线Fig.6 Hysteretic curves

2.3 骨架曲线

图7为试件的骨架曲线。各次加载中，第一阶段的骨架曲线变化趋势基本一致，每条曲线叠加呈现出统一的“S形”。同次加载中，当层间位移角相同时，第二阶段的梁端弯矩绝对值均小于第一阶段，且当层间位移角较小时两者的梁端弯矩值相差较大，随着层间位移角的增大其差值逐渐缩小，由此可推知，当经历了某一主震作用的顶底角钢自复位梁柱节点再次遭受余震作用时，较小的余震强度对节点抗弯能力的影响反而更大。除此之外，第二阶段的骨架曲线之间也各不相同，在层间位移角相同的情况下，加载次序较大的曲线其梁端弯矩的绝对值小于加载次序小的曲线，而加载的次序正反映了试件所受主震作用的强度大小，由此可知，顶底角钢自复位节点所经历的主震强度越大，其在某一地震强度的余震作用下承载力越小。

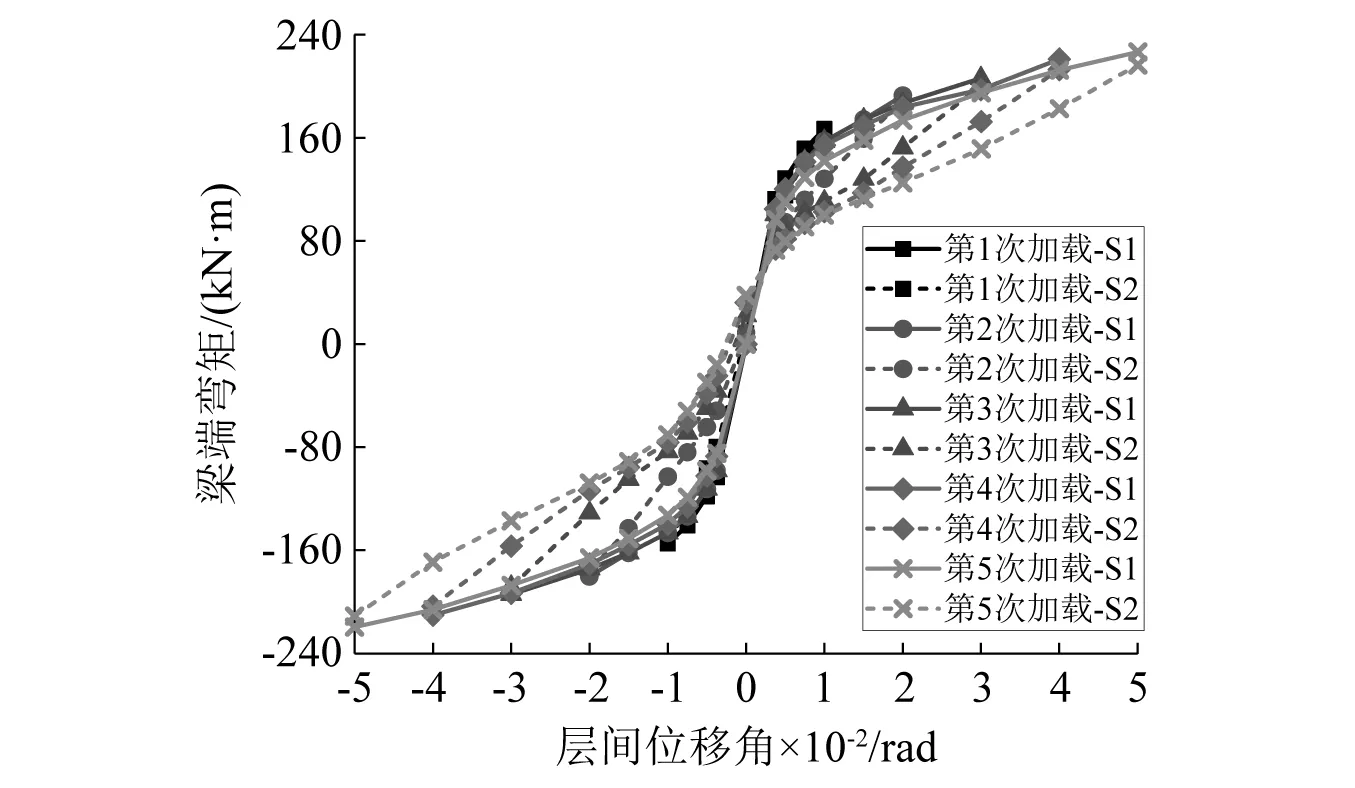
图7 骨架曲线Fig.7 Skeleton curves

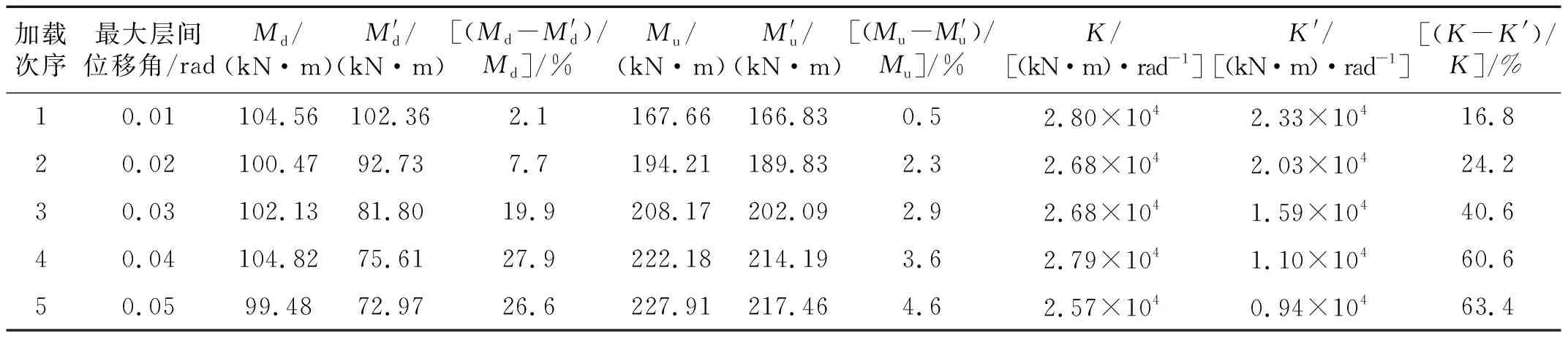
表2 节点力学性能Tab.2 Mechanical properties of connection

2.4 残余变形

残余变形是指地震作用后结构中不可恢复的变形，如果震后结构的残余变形过大，会导致建筑无法修复。对于顶底角钢自复位梁柱节点而言，主体梁、柱构件在地震作用下可基本保持弹性，而角钢作为金属耗能构件发生屈服后会产生塑性变形，并且钢绞线中不可避免会出现预应力损失进而导致节点的自复位驱动力降低及自复位性能减弱，这些情况是整体结构最终产生残余变形的主要原因。

图8为各次加载结束后试件的残余层间位移角，其中横坐标为最大层间位移角，对应各次加载中的位移荷载幅值。由图8可知，随着试件所经历的最大层间位移角逐渐增加，其残余层间位移角快速增大。当最大层间位移角不大于2%rad时，节点在两阶段的残余层间位移角几乎相同；而当最大层间位移角分别达到3%rad，4%rad，5%rad时，第二阶段的残余层间位移角相对第一阶段的增幅依次为47.6%，27.1%和10.6%，可知第二阶段的残余变形有所增大，不过此增幅与最大层间位移角之间的关系并不呈现单调递增的规律，这是因为余震或二次加载使得结构产生了额外的附加损伤，结构偏离加载的初始位置而在新的平衡位置处于稳定状态，因此残余变形变化的方向不具备规律性，这也与文献[19]中的结论相似。

已有研究结果[20]表明，当震后结构中的残余层间位移角超过0.5%rad时，从经济和技术的角度分析，该结构已失去修缮价值。参考上述结论对图8中的曲线插值计算可推知，当试件节点在单独主震作用的情况下，其最大层间位移角达到3.31%rad时对应的残余变形为0.5%rad，结构因此失去修复价值；若考虑主余震共同作用，其在经历余震时最大层间位移角为2.99%rad便会导致修复工作难以进行，相比单独主震作用其可承受的层间位移角峰值降低了10.7%，这说明当评判该自复位结构体系在震后的可修复性时有必要考虑主余震组合作用的影响。

图8 残余层间位移角与最大层间位移角的关系Fig.8 Relation between the maximum residual inter-storey drift ratio and the maximum inter-storey drift ratio

2.5 耗能能力

图9反映了试件的耗能随最大层间位移角变化的趋势。试件在第一阶段的耗能均大于第二阶段，且随着最大层间位移角的增大，两者的耗能相差逐渐变大，第二阶段的耗能减少程度由第1次加载时的9.7%逐渐提高至第5次加载时的31.9%，由此可见主余震作用对顶底角钢自复位节点的耗能能力影响突出，尤其当主震强度较大时，节点在余震作用下的耗能能力降低较为明显。

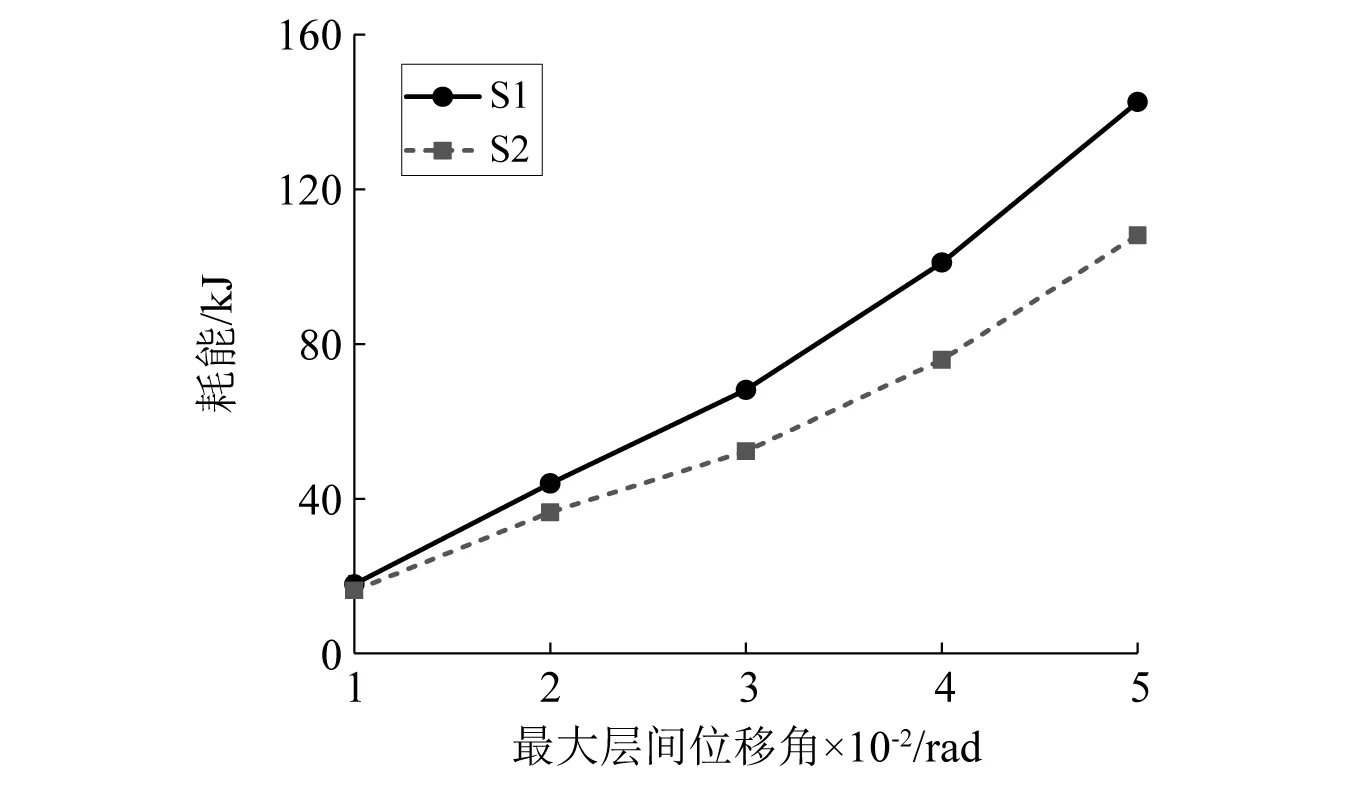
图9 耗能与最大层间位移角的关系Fig.9 Relation between the energy dissipation and the maximum inter-storey drift ratio

2.6 钢绞线拉力

由于钢绞线布置具有明显的对称性，遂仅选取一根钢绞线对其拉力变化进行分析，图10为各次加载过程中钢绞线拉力与梁端弯矩的关系图。随着加载次序的递进和最大位移荷载的增大，钢绞线拉力变化的范围不断扩大，并明显体现出关于加载方向的不对称性。

图11反映了钢绞线的最大拉力与最大层间位移角的关系。两阶段的钢绞线最大拉力随着最大层间位移角的增大而持续增大，且第二阶段的最大拉力均小于第一阶段，但减小程度相对较小，最大不超过4.2%。

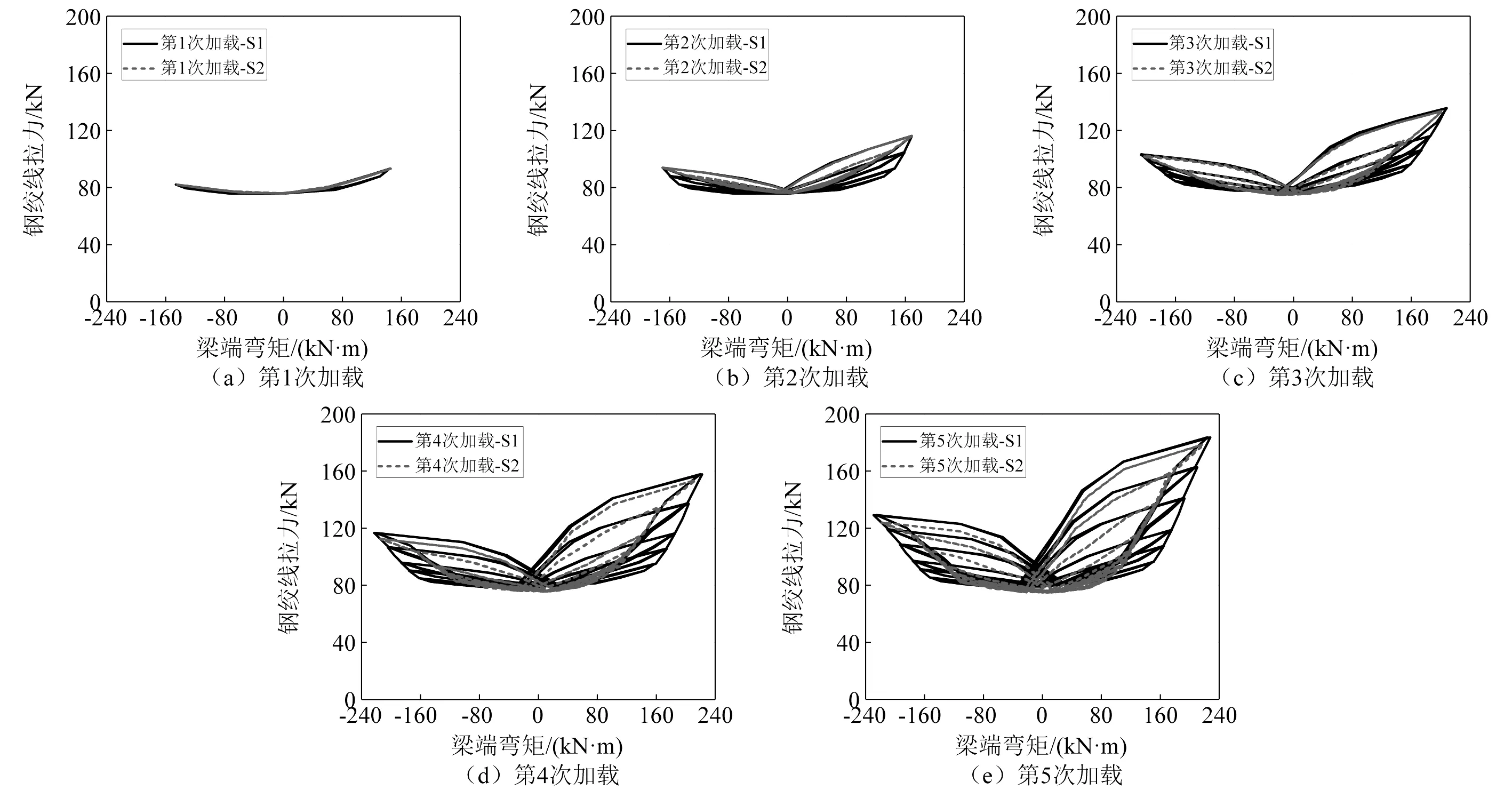
图10 钢绞线拉力Fig.10 Tension of strands

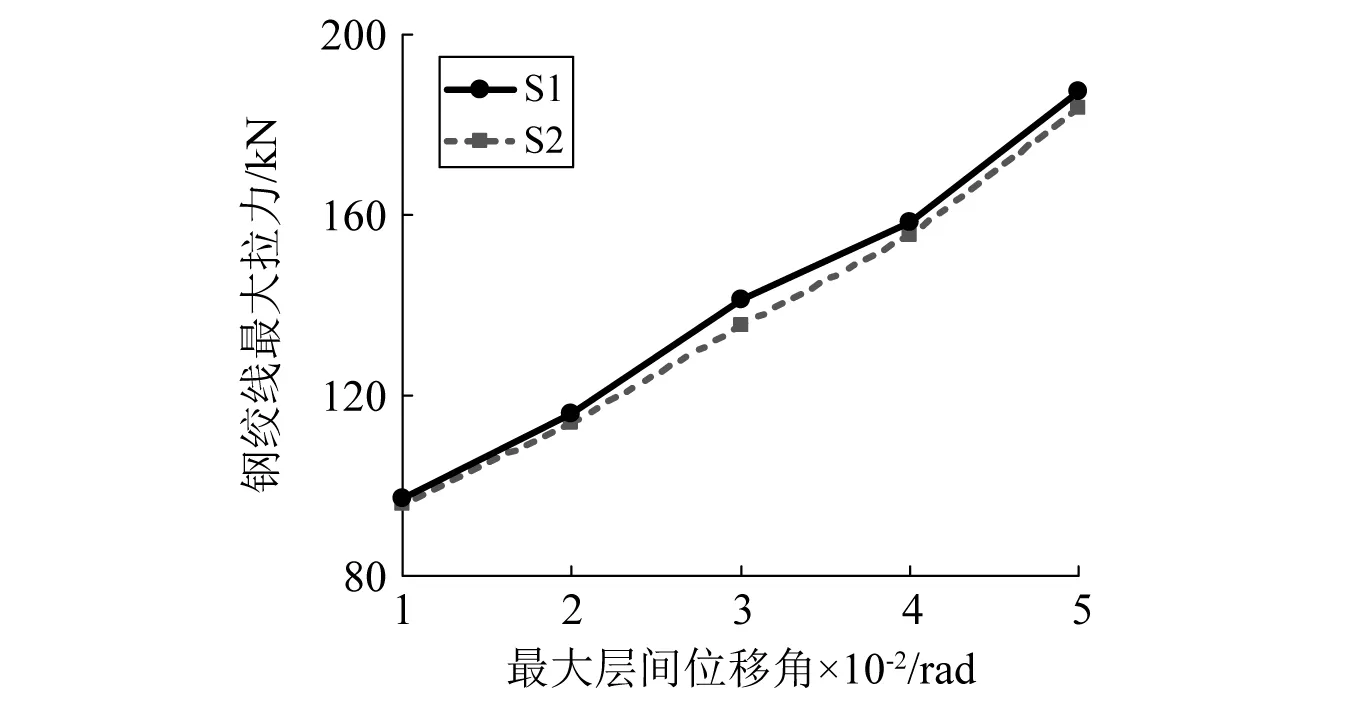
图11 钢绞线最大拉力与最大层间位移角的关系Fig.11 Relation between the maximum tension of the strand and the maximum inter-storey drift ratio

3 有限元模拟

3.1 建模方法

采用ABAQUS软件建立顶底角钢自复位梁柱节点的有限元模型。钢材属性的定义采用遵循Von Mises屈服准则的双线性随动强化模型，材料参数见表1，泊松比取0.3。钢绞线采用两节点空间桁架单元T3D2进行模拟，其他构件如梁、柱、角钢等均采用八节点六面体线性减缩积分单元C3D8R模拟。网格划分采用结构划分法，单元形状选择六面体。端板与梁加载端、加劲肋与钢柱、垫板与梁柱翼缘之间的连接均为焊接，有限元中通过tie连接进行模拟。构件之间的接触关系需要定义切向行为和法向行为，其中法向行为设置为hard contact，切向行为中的摩擦因数设置为0.35。为模拟锚具对钢绞线的约束作用，在钢柱翼缘与梁端板的锚固位置划分出一个与锚具尺寸相同的区域，并建立钢绞线端点和此区域的耦合约束。约束钢柱两端所有的平移和转动自由度，并限制梁端平面外位移以模拟侧向支撑的作用。螺栓预紧力采用荷载模块中的bolt load功能进行模拟，对钢绞线施加预应力则采用等效降温法，该方法依据的公式如下

P=αEAΔT

(1)

式中:P为需要施加的预拉力值；α为钢绞线的热膨胀系数，取1.35×10-5；E为钢绞线的弹性模量，根据试验取2.0×105MPa；A为钢绞线束的截面积，取140 mm2；ΔT为温度降低值。

3.2 模拟结果及分析

根据试验加载历程，对有限元模型的梁端施加循环荷载，由于篇幅所限，以最大位移荷载为0.03 rad的加载为例，给出节点的有限元模拟结果(见图12)。图12(a)反映了节点在第二阶段最大位移转角时的受力变形，可见梁柱主体结构处于弹性状态，塑型变形集中于角钢上，从而验证了顶底角钢自复位节点具有损伤可控性的特征，此时受拉侧的角钢如图12(b)所示，角钢柱肢脱开柱面垫板，并于楞线附近及柱肢螺栓孔区域发生屈服，待加载结束后，角钢柱肢边侧发生了与试验现象相同的翘曲塑性变形，且角钢楞线附近区域出现明显的残余应力，如图12(c)所示。将有限元模拟得到的节点滞回曲线与试验结果进行对比(见图13)，两者的滞回曲线能够较好吻合，两阶段的最大承载力误差分别为5.2%(S1)和2.0%(S2)，初始转动刚度误差为8.2%(S1)和8.8%(S2)，以上误差相对较小，由此可判定该有限元模型能够较为准确地反映节点在两阶段加载下的滞回性能特征。

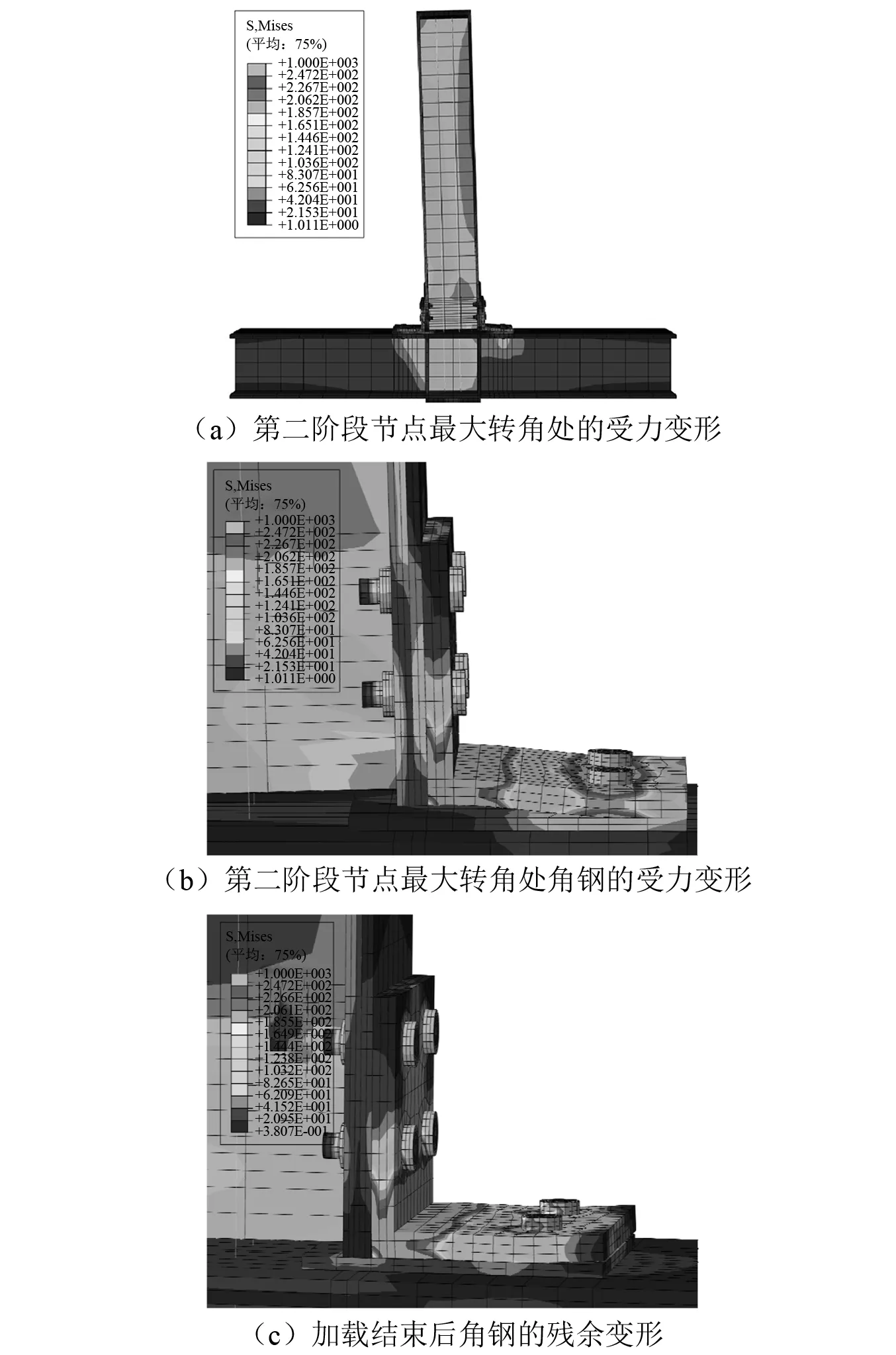
图12 最大位移荷载为3%rad时节点的有限元模拟结果Fig.12 Results of finite element simulation with a maximum inter-storey drift ratio of 3%rad

顶底角钢半刚性梁柱节点具有延性好、耗能优、施工方便等特点，在工程实践中应用较为广泛[21]。建立顶底角钢半刚性节点的有限元模型，各部分构件的材料、尺寸与自复位节点相同，并对其施加相同的位移循环荷载，提取滞回曲线结果与自复位节点进行比较，对比结果见图13，可知顶底角钢半刚性节点的滞回曲线较为扁平，承载力相对较低，且残余变形较大。表3总结对比了两种节点在两阶段加载下的各项性能参数，由于预应力钢绞线的存在，自复位节点的残余变形总体较小，并且其梁端最大弯矩、初始转动刚度、耗能能力均大于顶底角钢半刚性节点。第二阶段的加载对两种节点的承载力影响均较小，两种节点的梁端最大弯矩降低均为3%左右，而自复位节点和顶底角钢半刚性节点在第二阶段的初始转动刚度则大幅下降，分别降低了41.1%和69.6%，其中自复位节点的刚度下降相对较小，这是因为自复位节点中预应力钢绞线为节点提供了较大的初始刚度。对比两种节点的残余变形，顶底角钢半刚性节点虽然由于残余变形的方向无规律性而使得其在第二阶段加载后略有减小，但总体上远大于自复位节点。自复位节点与顶底角钢半刚性节点在第二阶段加载中耗能分别下降了23.2%和27.7%，降低程度相差不大，这是因为两种节点的耗能方式均是通过角钢塑性变形进行耗能，且角钢尺寸、布置方式均相同，角钢受损后其耗能能力下降程度相似。由上述分析可知，相对于顶底角钢半刚性节点，自复位节点不仅具有自动复位的优势，其在单独主震的作用下抗震性能也相对较好，并且其在余震作用下的抗震能力削弱程度也相对略小。

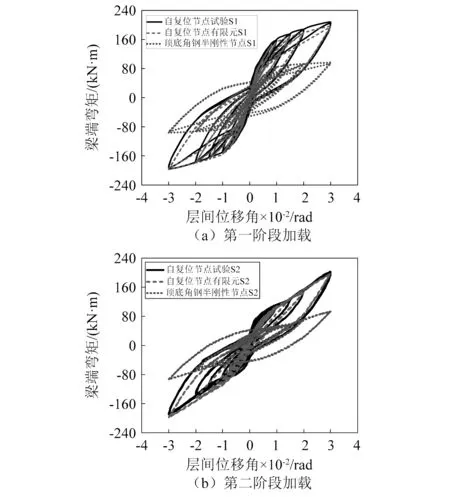
图13 有限元模拟得到的滞回曲线对比Fig.13 Comparison of the hysteresis curves obtained by finite element simulation

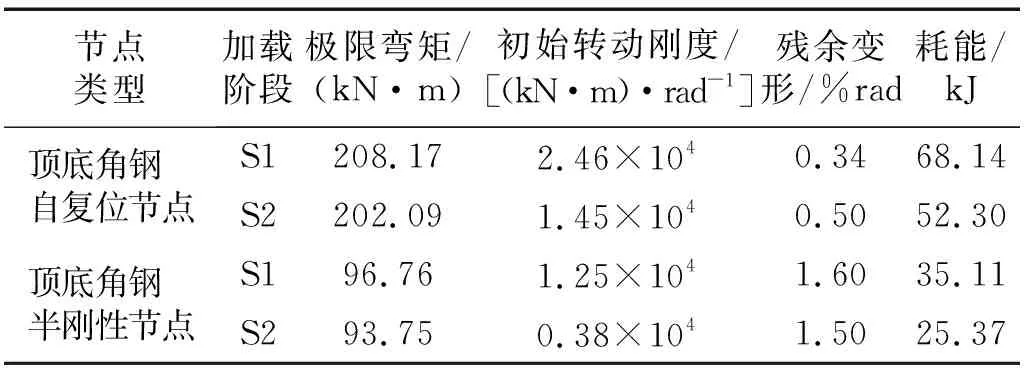
表3 两种节点抗震性能有限元模拟结果对比Tab.3 Comparison between the seismic performance results of the two connections in finite element simulation

4 结 论

(1)通过试验与有限元模拟，对顶底角钢自复位梁柱节点进行连续的拟静力加载以模拟节点经历主余震作用，结果表明该自复位节点的梁、柱主体构件在整个加载过程中始终处于弹性状态，塑性变形集中于耗能构件角钢中，这说明顶底角钢自复位钢框架梁柱节点在主余震共同作用下依然具有损伤可控性。

(2)相比于单独主震作用的情况，主余震作用降低了顶底角钢自复位梁柱节点的滞回性能，其中节点的耗能能力、初始转动刚度降低明显。对于承载力而言，节点所经历的主震强度越大，其在某一强度的余震作用下承载力越小。余震作用下结构的残余变形也许会增加，当地区内抗震设防烈度较大时有必要考虑主余震作用对自复位框架结构体系可修复性的影响。

(3)与顶底角钢半刚性梁柱节点相比，顶底角钢自复位节点不仅具有自动复位的优势，其在单独主震的作用下抗震性能也相对较好，不仅如此，其在余震作用下的抗震能力削弱程度也相对较小。

Vol．41 No．12 2022