自适应多尺度噪声调节二阶随机共振增强方法

李国英， 王诗彬， 杨志勃， 李继猛， 陈雪峰

(1. 西安石油大学 经济管理学院，西安 710065；2. 西安交通大学 机械制造系统工程国家重点实验室，西安 710049；3. 燕山大学 电气工程学院，河北 秦皇岛 066004)

随机共振[1]方法利用噪声实现随机共振现象的产生，从而实现振动信号中故障特征增强，使其在检测低信噪比的信号中具有显著的优势，更有利于检测淹没于强噪声背景中的早期微弱故障，随机共振理论虽然经历了近40年的发展和研究，但想要让随机共振理论更好地服务于工程实践当中，仍需要开展大量的理论研究，并进行严谨的实验验证，提高随机共振理论的工程适用能力。

经典随机共振方法虽能利用噪声实现微弱信号的非线性增强，但绝热近似理论中绝热近似条件的限制，使得其仅适于处理极低频或极小幅值的信号。而工程实践当中各种机械装备零部件的故障特征频率往往都是几十、几百甚至上千赫兹，远远大于1 Hz。对于这样地高频微弱信号检测，直接利用双稳随机共振很难检测。为了解决高频信号这一类大参数信号地特征检测，学者们提出了自适应随机共振[2-5]、各种大参数随机共振算法[6-9]、移频变尺度随机共振[10-13]等的方法，虽一定程度上增强了信号特征，但经过单一随机共振系统，原始信号中的噪声能量并未被充分利用，系统响应中依然含有较多的噪声。

考虑到多尺度带限噪声[14-15]对随机共振的影响，并基于随机共振特殊低通滤波器的数学本质，借助“双重积分”[16-19]实现噪声的重复利用，本文深入研究了自适应多尺度噪声调节的二阶随机共振增强[20-28]方法，以进一步改善随机共振检测效果。

小波变换的过程相当于用了一个低通、若干个高通滤波器，将原始信号分解到一些频段内，这些频段相互正交，实现了既看到“森林”(信号的全貌)，又看到“树木”(信号的细节)的目标。本文噪声强度地调控考虑利用小波变换的多分辨分析特性，从不同尺度处理信号，将输入信号和噪声划分到不同频带，实现不同频带信号和噪声强度大小的控制。

因此，在He等[29]提出的1/f多尺度噪声调节随机共振算法的基础上，研究了可以将频带划分更加精细的连续小波变换的多尺度噪声调节方法，提出了以协同信噪比(collaborative signal to noise ratio, CSNR)为目标函数，基于Paul小波的多尺度噪声控制二阶随机共振增强方法，实现了强噪声背景下微弱故障信号特征地增强提取，并通过仿真实验及工程实际应用验证了提出方法的有效性。

1 协同信噪比指标

定量表征随机共振增强能力的测度指标可以定量评价随机共振的增强效果和信号失真程度等性能，随机共振系统中常用的评价指标有：针对周期信号的随机共振现象的指标主要为信噪比、驻留时间分布及信噪比增益等；针对非周期信号的随机共振现象的评价指标主要有相干函数、相关系数等。测度指标的构造直接会影响运算算法的有效性和准确性，针对不同的系统性能需求，需要使用不同的测度指标。

协同信噪比指标，是在传统信噪比的基础上，综合考虑目标信号频谱中最高谱峰位置、表示两个信号之间相关性的互相关系数、残余噪声方差及表征信号周期性的过零点比率等成分构造出来的，这样可以充分发挥各个组成成分的优势，实现在目标信号频率不确定的情况下，更有效地表征检测结果的有效性和准确性，更有效地定量评价随机共振系统响应输出的性能和特征增强程度[30]。

协同信噪比指标CSNR用RCSN表示其计算公式为

(1)

式中：RCSN为协同信噪比；RSN为信噪比；A为最高谱峰与次高谱峰的差值；C为互相关系数；Nvar为残余信号方差；Rzc为过零点比率；sgn(·)为符号函数。

信噪比主要指随机共振输出中主成分与残余成分的比值。主成分是驱动频率的最高谱峰幅值和输出频谱中的最大值。残余成分是与信号中主成分对应的其他成分。可以通过使用输出频谱中最高谱峰对应的最大值取代输入信号频率值作为目标信号的频率来获得输出信号的信噪比。

互相关系数，是用来表征两个信号相似程度的测度指标。互相关系数的绝对值可以定量表征两个信号之间的相似程度。

残余信号方差可以描述信号经过处理后输出响应的残余噪声分布的情况，是用采集到的原始振动信号减去用最高谱峰位置频率得到的重构信号后剩余的部分。残余信号方差可以评价信号残余噪声分量中含有多少的周期信号成分。

过零点比率主要指的是信号中过零点的实际数值与理论数值之比，是一种在时域上描述信号周期性的指标。过零点比率的值一般在[0,1]，它的取值趋于0时表明信号周期性特征弱，它的取值趋于1时表明信号的周期性特征强。

|C|，|RSN|和Nvar全部归一化处理使其取值范围变为(0,1]。这部分可以让检测结果更加逼近真实信号的频率值，再借助A可进一步凸显目标频率的谱峰，因为A越大，说明目标信号的最高谱峰与次高谱峰的差值越大，最高谱峰就越突出，越有利于目标频率地检测，从而更好地调整了随机共振的观测效果。

2 基于Paul小波的多尺度噪声控制方法

文中选用Paul小波变换作为实现多尺度噪声控制的方法。Paul小波的时域波形图，如图1所示。

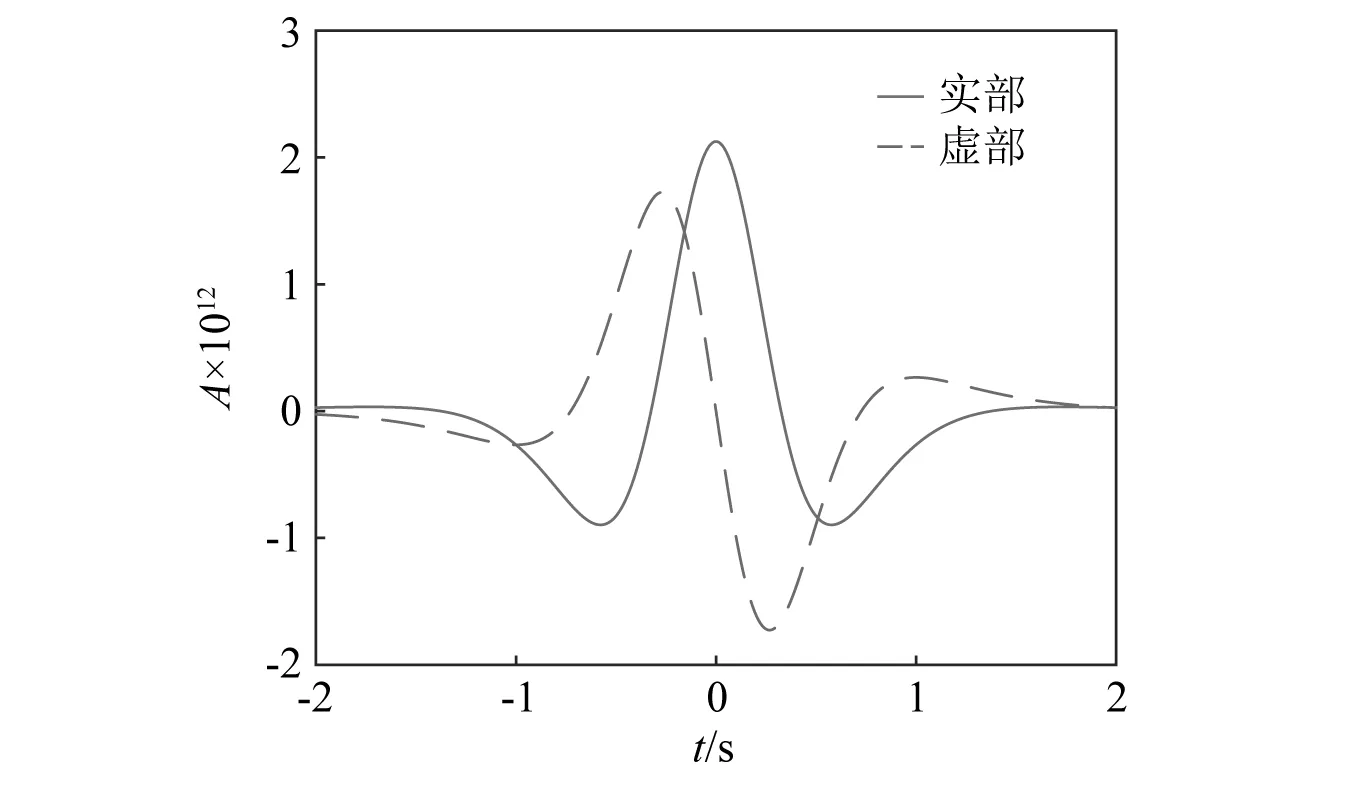
图1 Paul小波时域图Fig.1 The time domain waveform of Paul wavelet

用Paul小波变换实现调控多尺度噪声的方法如下所述。

假设x(t)为一个含有噪声的周期信号，其采样频率为fs，x(t)的连续小波变换公式可以表示为

(2)

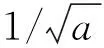
W(a,b)系数定量表征信号x(t)与母小波ψ(t)之间的相似程度。对于在一定位置b给定的尺度下，W(a,b)给出相似程度。

根据傅里叶变换的卷积定量，式(2)可以进一步表示为

(3)

由基本小波或母小波ψ(t)通过伸缩a和平移b产生一个分析小波ψa,b(t)。有

(4)

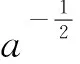
在文中，母小波Paul的表达式及其傅里叶变换[31]如下

(5)

(6)

式中： j为复数单位；a为尺度因子；m为Paul小波函数的消失矩阶数，阶数m默认值一般为4；ω为频率；H(ω)为Heavisidestep阶跃函数，ω>0时，H(ω)=1，ω≤0时，H(ω)=0。

即Paul小波的频率表达式为

(7)

一般情况下，当消失矩阶数m值越大时，时域波形中函数的幅值会随之快速变化，小波衰减也会越快，这时表现为时域宽度趋窄幅值趋于增大；当在频域上进行分析时，函数的波动趋势逐渐变缓，这时表现为频域的宽度趋于增大，幅值趋于减小。因此，较大的消失矩阶数m值对增强信号的时间分辨率更为有利，较小的消失矩阶数m值对增强信号的频域分辨率更为有利。

经过平移伸缩后，Paul小波可表示为

(8)

多尺度噪声调控过程中最为重要的是合理地选择分解尺度L。因为当分解尺度L太大时，在分解的过程中会增加低频干扰，影响二阶随机共振增强模型实现随机共振响应的效果；当分解尺度L太小时，则会使信号和噪声无法有效分离，调控失败。工程应用中，一般近似的将小波频谱中能量最多的频率值作为小波的中心频率，因此，需要选择合适的分解尺度使得中心频率始终在被分析的信号带宽内。

Paul小波的中心频率ωc=2πfc，可以表示为

(9)

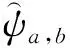
因为预期的目标信号频率必须包含在Paul连续小波经过连续小波变换后得到的信号中才有意义，因此，确定分解尺度的原则可以设定为这一点。Paul小波变换后在每一尺度下都会得到一个信号频率，这个频率被称之为伪频率，伪频率可以由式(10)计算得出

(10)

式中：fa为尺度a下Paul小波变换后的伪频率；fc为Paul小波函数的中心频率；fs为信号的采样频率。

利用分解尺度的确定原则可以得到分解尺度L

fa=L=f0

(11)

从而进一步得到1～L层分解的Paul小波变换系数W

W={W1,W2,…,WL}

(12)

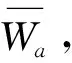
(13)

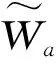
3 自适应多尺度噪声调节二阶增强方法的算法流程

自适应多尺度噪声调节二阶增强方法的目标是以CSNR为目标函数，实现二阶增强随机共振的不同尺度下噪声强度的调节参数能够自动地最优化选取。当目标频率范围内的CSNR达到最大值时，它所对应的调节参数为最优参数，从而实现目标信号地有效检测。其算法流程如图2所示。算法流程的详细步骤如下。

步骤1信号预处理。利用传统的信号处理方法对采集到的振动信号进行如包络解调等的初步处理。为了保留信号和噪声的多尺度信息，在使用包络解调方法时不对原始信号进行滤波。

步骤4二阶增强随机共振检测。用网格搜索算法，以CSNR为目标函数，以获得最优的多尺度噪声调控参数β。具体流程如下：针对噪声强度的调节参数β搜索范围内的每一个β值，进行Paul小波重构，并分别通过二阶随机共振增强模型，求出每一个对应的输出CSNR，直到找到CSNR的最大值，并保存这个最大CSNR及其相应的最优参数值β。当噪声强度调节参数β超出搜索范围时，改变参数β，并转回步骤2，重新设定β的初始值，及相应的搜索范围、搜索步长。

步骤5二阶增强随机共振输出优化结果。用最优的噪声强度调节参数β得到多尺度调整下的小波系数集合，基于Paul小波得到最优的重构信号，经过二阶增强随机共振系统，得到系统输出响应，在系统输出响应频谱中突出的谱峰所对应的频率即为检测目标信号的特征频率。

相对于信噪比指标为测度函数的随机共振而言，其检测能力有了较大地提高，不仅可以使低频信号被有效地检测，而且更适合于高频信号地随机共振检测，大大提高了随机共振的工程适用性。

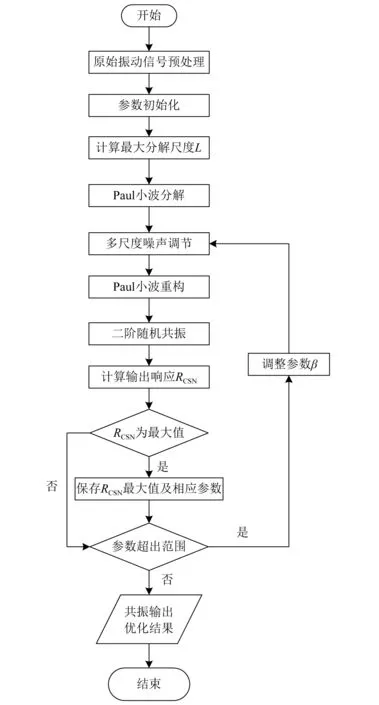
图2 自适应多尺度噪声调节二阶随机共振增强算法流程Fig.2 The algorithm flow of the second order stochastic resonance enhancement method based on the adaptive multiscale noise tuning

4 仿真实验与工程应用

4.1 仿真实验

为了验证第3章提出方法的有效性，首先构造一组仿真信号进行验证，其次用采集到的一组滚动轴承故障数据进行进一步地验证。

4.1.1 数值仿真

构造一个仿真信号

对客户的责任，让炜冈在每开发一个产品之前都会进行至少4个月的市场调研，包括客户的接受程度、产品的智能化程度、环保性，以及其在市场的生命力，从而保证该产品可以帮助客户有所提升。

x(t)=A0sin(2πf0t)+n(t)

(14)

式中：A0为仿真信号的幅值，A0=0.12；f0为信号频率，f0=150 Hz；n(t)为添加均值为0、方差为2的高斯白噪声。采样频率为fs=4 096 Hz，数据长度为8 192，其信噪比为-21.50 dB。数值仿真原始信号时域波形，如图3(a)所示。由图3(a)可知，噪声已完全淹没了周期信号分量。数值仿真原始信号的频域谱图，如图3(b)所示，没有任何有用的信息。

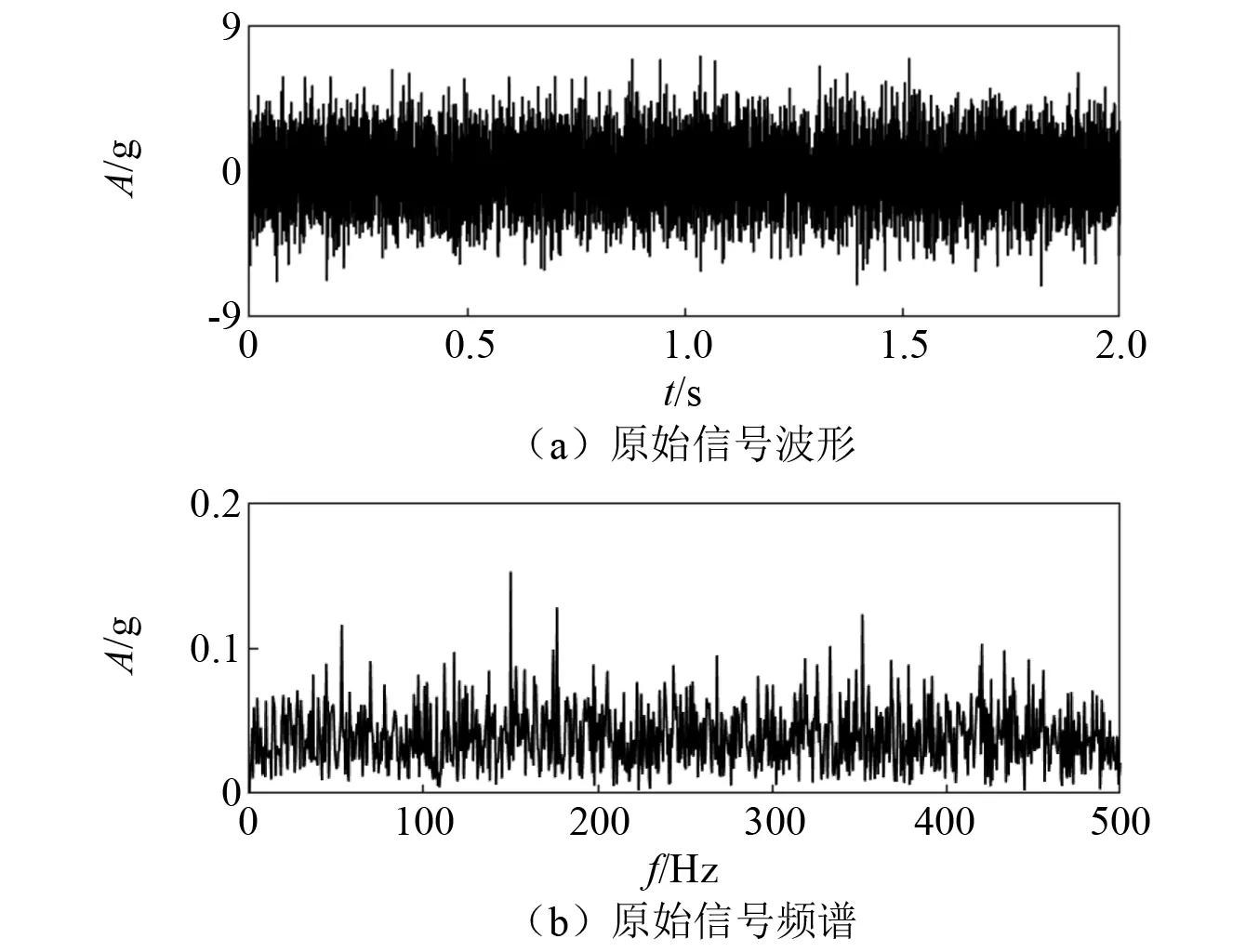
图3 数值仿真原始信号波形及其频谱Fig.3 The vibration waveform and the spectrum of the original simulation vibration signal

将原始信号采用本文所提多尺度噪声调节方法进行处理，其中噪声强度调节参数β的取值范围设为[10,40]，搜索步长为0.2，Paul小波的消失矩设置为6，经过第3章算法流程，寻优求得最大分解尺度为26，协同信噪比指标最大值为7.528 6，此时对应的系统响应输出时域波形及其频谱，如图4所示。

可以看出，图4(a)中系统响应信号的时域波形中已经出现了较为明显的周期性特征，振动幅值较大；图4(b)的频谱图可以清晰地看到显著的谱峰，对应的频率正是周期信号150 Hz的频率值，振动幅值大，检测效果较好。

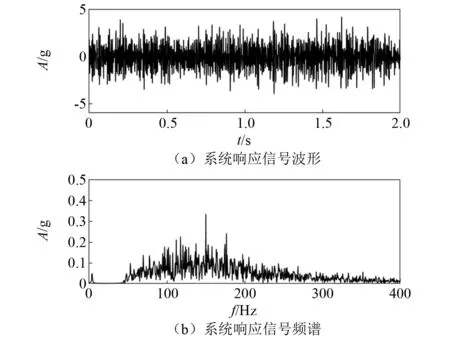
图4 数值仿真信号所提方法的输出波形及其频谱Fig.4 The output signal and the spectrum of the proposed method for the simulation signal

4.1.2 实验验证

选用SpectraQuest公司开发设计的机械故障模拟实验台SQI上的实验数据进行验证。试验中将一个加速度传感器安装在电动机前轴承的轴承支座上，用亿恒数据采集系统获取实验中的故障动态信号，轴承型号为SKF 6203，采样频率设置为6 400 Hz，电动机的输出转速为1 433 r/min。

根据电动机前轴承的各种几何参数在设定工况下可获得轴承内圈的特征为117.52 Hz。SQI机械故障模拟实验台电动机前轴承的原始振动时域波形、频谱及其包络谱，如图5所示。

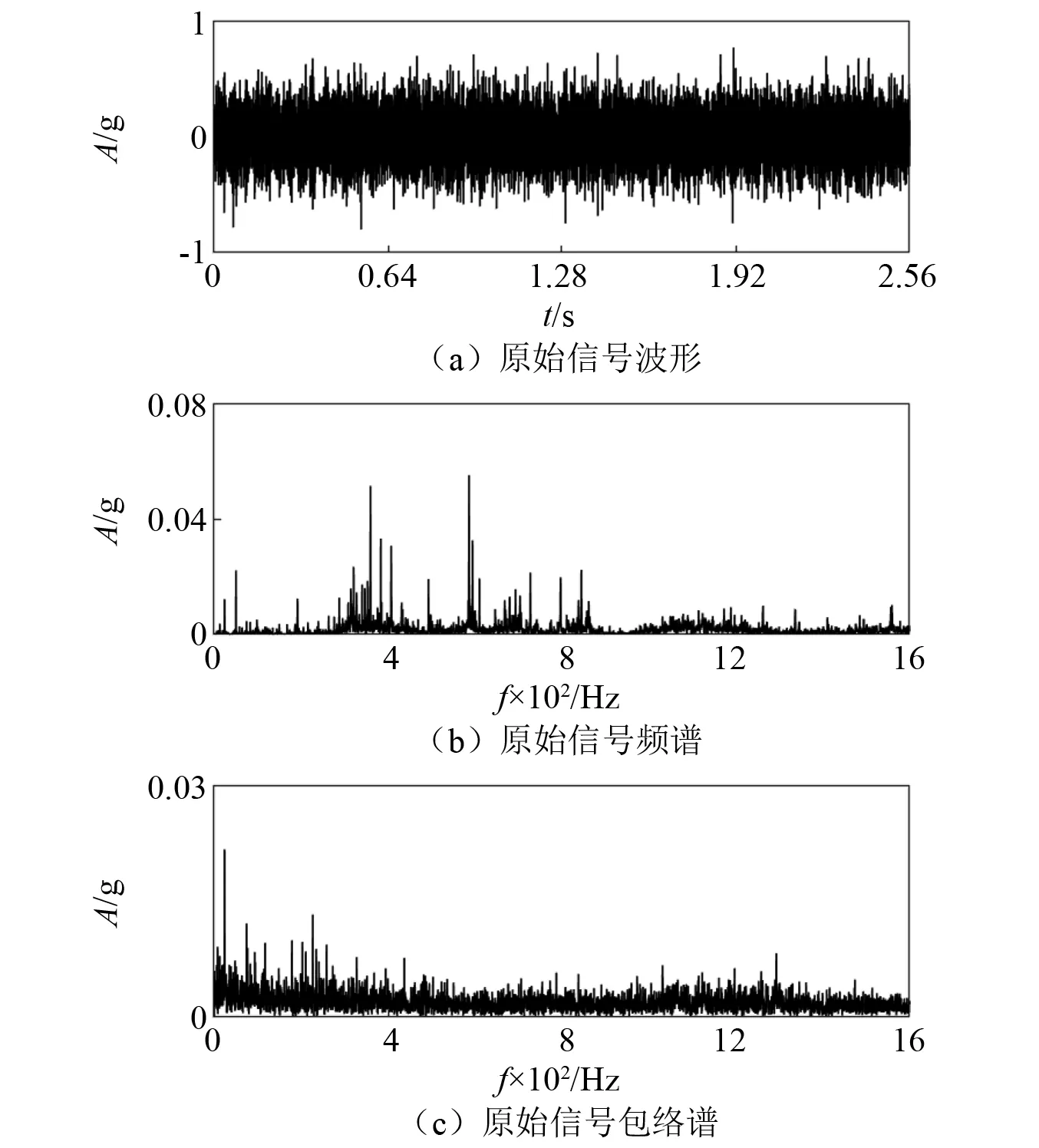
图5 实验数据信号波形、频谱及其包络谱Fig.5 The vibration waveform and the spectrum and the envelope spectrum of the experimental data

图5(a)原始信号的时域波形杂乱无章，没有明显的周期性故障特征；图5(b)的原始信号频谱中，转频信息依稀可见；图5(c)包络谱图中转频分量23.83 Hz比较突出，117.2 Hz的故障特征频率成分很不起眼，幅值很小。

采用文中提出的方法进行处理，得到的系统响应及其频谱，如图6所示。图6中，Paul小波的消失矩设置为5，噪声强度调节参数β的取为[1,20]，搜索步长为1，可求得连续小波变换的最大分解尺度为27，其系统响应RCSN=66.98。可以看出，图6(b)系统的输出频谱中，故障特征频率谱峰比较显著，自适应多尺度噪声调节二阶随机共振增强方法有效地提取出了轴承目标信号的故障频率特征，充分证明了本文方法的有效性。

图6 实验数据所提方法的输出波形及其频谱Fig.6 The output signal and the spectrum of the proposed method for the experimental data

4.2 工程应用

选用某风场联合动力风电机组的状态监测数据进行分析，在对该风场风电机组运行状态检测时，9#机组发电机前轴承幅值很大，振动超标。9#机组的主轴为双轴承支撑。发电机为双馈异步发电机，齿轮箱与发电机通过复合联轴器连接。该风场风电机组传动系统的传感器测点总共有12个，收集风电机组齿轮箱、轴承等关键部件的运行状态信息。风电机组发电机在数据采集时的实时参数为：转速1 453 r/min，采样频率12 800 Hz，数据长度16 384点。

风电机组发电机前轴承的主要技术参数，如表1所示。根据参数可以计算得出风电机组发电机前轴承内圈的故障特征频率为131.1 Hz。

表1 风电机组发电机轴承参数Tab.1 The bearing parameters of the wind turbine generator

发电机前轴承采集信号的原始波形、频谱及其包络谱，如图7所示。由图7(a)可知，振动信号的时域波形较为杂乱，没有明显的周期性特征；由图7(b)可知，原始振动信号频谱中干扰分量很多，未能提供相关的故障信息，也没有非常明显的轴承故障特征频率成分；由图7(c)可知，转频成分24.22 Hz较为明显，130.5 Hz的频率成分也较为明显，这个分量与发电机的轴承内圈的故障特征频率131.1 Hz相一致，但干扰频率成分大量存在，且130.5 Hz的频率分量所对应的幅值很不明显，难以有效识别。

发电机前轴承采集信号采用文中提出的基于协同信噪比指标的二阶多尺度噪声调节随机共振增强方法对风电机组发电机前轴承的振动信号进行处理，得到的系统响应及其频谱，如图8所示。

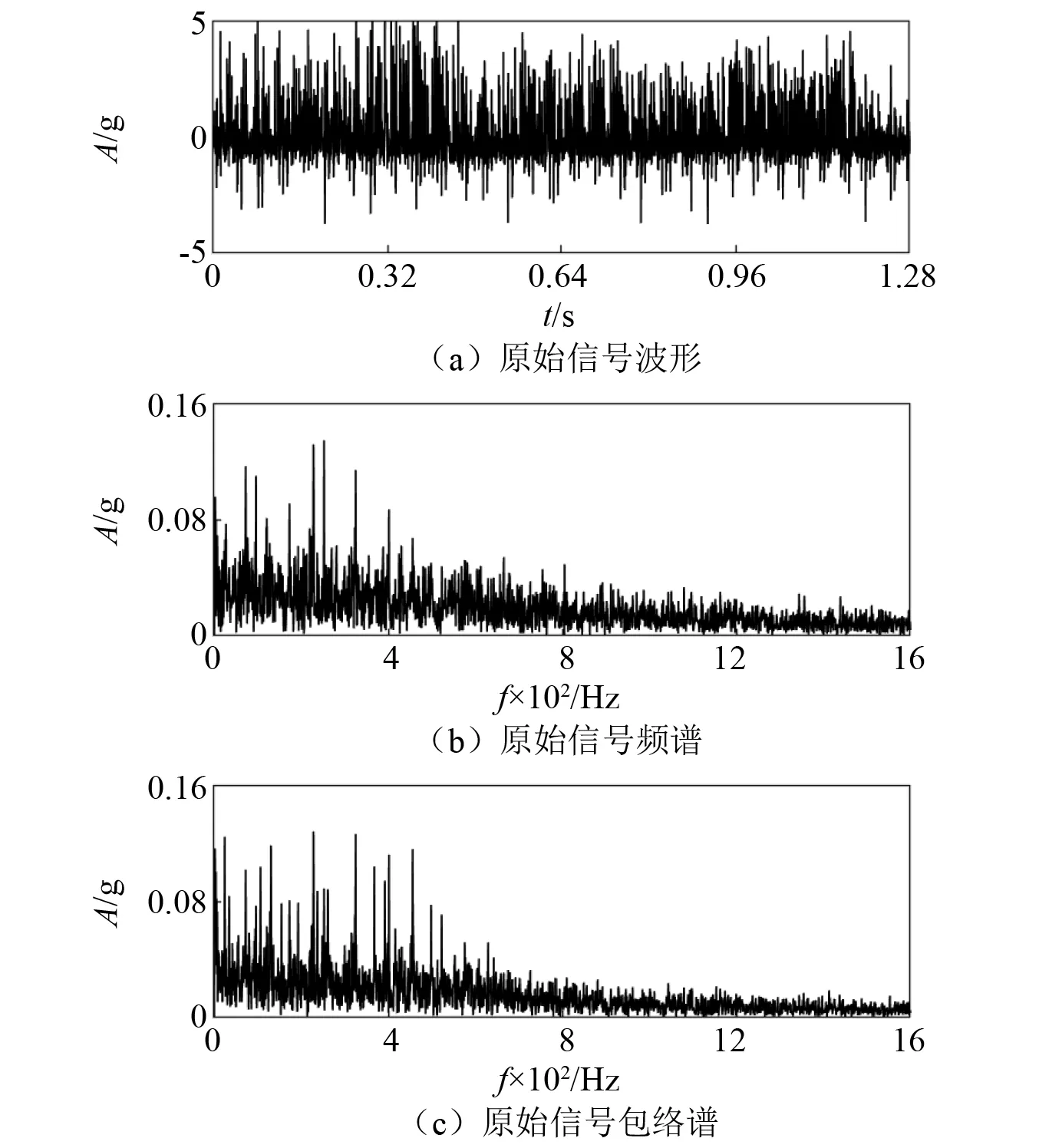
图7 工程应用数据信号波形、频谱及其包络谱Fig.7 The vibration waveform and the spectrum and the envelope spectrum of the engineering application data

其中，以CSNR为目标函数，双稳态模型的系统参数为a=1，b=1，利用Paul小波进行多尺度的噪声调节，Paul小波的消失矩设置为5，经过上述的算法流程，求得的连续小波变换的最大分解尺度为24，噪声强度调节参数β的取值范围为[1，20]，搜索步长为1，最终得到如图8所示的检测结果。其系统响应RCSN=8.44。可以看出，在多尺度噪声调节的二阶随机共振增强算法中，非常有效地提取出了风电机组发电机前轴承振动目标信号的故障频率特征，系统响应频谱中相应的目标信号频率谱峰非常突出，周围的干扰频率分量幅值很小，本工程应用案例充分证明了本文所提方法的有效性。

5 结 论

(1) 针对二阶随机共振增强方法在应用过程中存在噪声调节较难的不足，考虑到小波变换的多分辨能力，小波变换的过程相当于用了一个低通、若干个高通滤波器，将原始信号分解到一些频段内，这些频段相互正交，从不同尺度处理信号，将输入信号和噪声划分到不同频带，来实现不同频带信号和噪声强度大小的控制。提出了以协同信噪比为目标函数，基于Paul小波的多尺度自适应噪声控制二阶随机共振增强的方法，利用小波变换具有的多分辨能力以及随机共振对带限噪声的敏感能力，调控不同尺度的噪声强度，促进随机共振地发生。在此基础上，提出了自适应多尺度噪声调节二阶随机共振增强方法的算法流程。

(2) 借助数值仿真信号和SQI实验台实验数据对方法的有效性进行了验证，最后将其应用于某风场风电机组发电机前轴承内圈故障特征地增强提取上，充分证明了本文提出方法的有效性和实用性，不仅降低了多参数联合调整的复杂性，实现了多参数的自适应选取，而且可实现任意频率信号特征地增强提取。