贴片误差和扭矩对输电铁塔角钢应变数据的影响

岑添添，王璋奇

（华北电力大学 机械工程系，河北 保定 071003）

0 引言

随着我国电量需求的不断增长，输电线路不断增加，输电铁塔的数目也在逐渐增多。由于构造简单、价格便宜和运输方便，角钢被广泛运用于输电铁塔结构中。为了确保输电线路的稳定运行，需要对输电铁塔角钢构件的力学性能进行充分研究。输电铁塔角钢的力学性能研究分为实验研究和仿真模拟分析。在实验研究方面，主要实验内容有输电铁塔角钢构件的受压承载力实验[1-4]、低温冲击韧性和疲劳实验[5-9]以及受拉承载力实验[10]。在仿真模拟分析方面，主要研究内容为构件几何初始缺陷、残余应力对角钢轴心受压构件稳定性能的影响[11-12]。此外，文献[13]研究了开/合角等边角钢的整体稳定性和经济性；文献[14]研究了斜材布置方式对构件极限承载力的影响。

在角钢构件的实验过程中，尤其输电铁塔的结构实验，需要用到应变片进行应变测量[15]，并利用应变片的测量值计算构件的轴力。在实验贴片过程中可能出现贴片失误[16]。如果忽略这些失误而直接使用测量读数进行轴力计算，可能会导致轴力测量失真。输电铁塔角钢在使用过程中的受力状态复杂，角钢可能同时受到弯、压（拉）、扭的综合力作用。由于弯矩和扭矩的存在，角钢同一截面上各点应力不相等，这导致贴片测量的结果与实际值存在一定的偏差；同时，扭矩会导致应变片横向效应，进一步造成测量误差的增大。

目前，关于输电铁塔角钢的研究主要集中在轴向受压稳定性方面，而少有关于贴片误差和角钢扭矩引起的角钢应变测量失真问题的研究。为此，本文推导了双肢连接角钢的轴力计算公式；以 L140×12规格的双肢连接角钢为研究对象进行有限元分析，提取测点应变值；通过轴力计算公式计算得到存在贴片误差和扭矩时的角钢轴力，并与所施加的载荷进行比较；通过轴力误差研究贴片误差和扭矩对输电铁塔角钢应变测量的影响。

1 真型实验中角钢的轴力计算

1.1 应变片的横向效应

横向效应是指垂直于应变主轴的应变引起应变片电阻变化的效应。除了理想应变片外，横向效应存在于每个实际的应变片中。在应变测量过程中，单向应力状态下，应变片电阻值变化与应变片形变的关系可表示为：

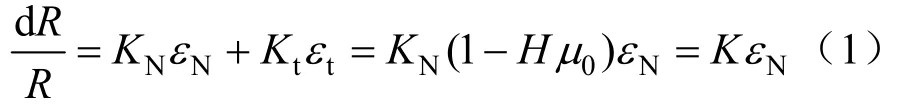
式中：εN、εt分别为平行于和垂直于应变片主轴的应变，且εt=-μ0εN（μ0为试件材料泊松比）；KN、Kt分别为应变片的轴向和横向灵敏系数；称H=Kt/KN为应变片的横向效应系数；K为应变片的灵敏系数，通常由实测来确定的。应变片自身布置导致的横向效应影响可通过出厂前的实测来克服。

然而，当试件处于非单向应力状态或应变片轴向与主应力方向不平行时，εt=-μ0εN不再成立，此时：

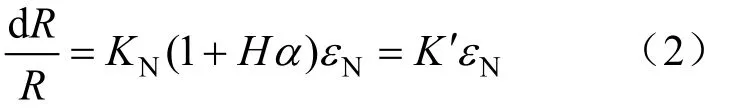
式中：α=εt/εN。

当试件发生εN的应变时，应变片电阻丝的电阻变化为dR/R=K′εN，则应变仪读数为：

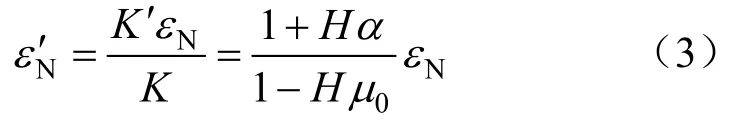
由此可见，当应变片的使用条件不是单向应力条件时，应变仪的读数并非实际的试件应变值。

1.2 双肢连接角钢轴向力计算方法

在输电铁塔真型实验中，一般将应变片贴在角钢基准线上。贴片方式如图1所示，其中X.1、X.2代表应变片1、2。对于双肢连接角钢，由于是对称连接，因此认为各个螺栓孔所承受的力是一致的，故可以将每一肢上所有螺栓孔的力简化等效成为一个集中力F/2；两肢上的集中力F/2又关于x0-x0轴对称，因此可将2个集中力F/2简化成合力F，如图2所示。图中，x0-x0、y0-y0为角钢的2个主轴，其具体位置可查看规范手册。

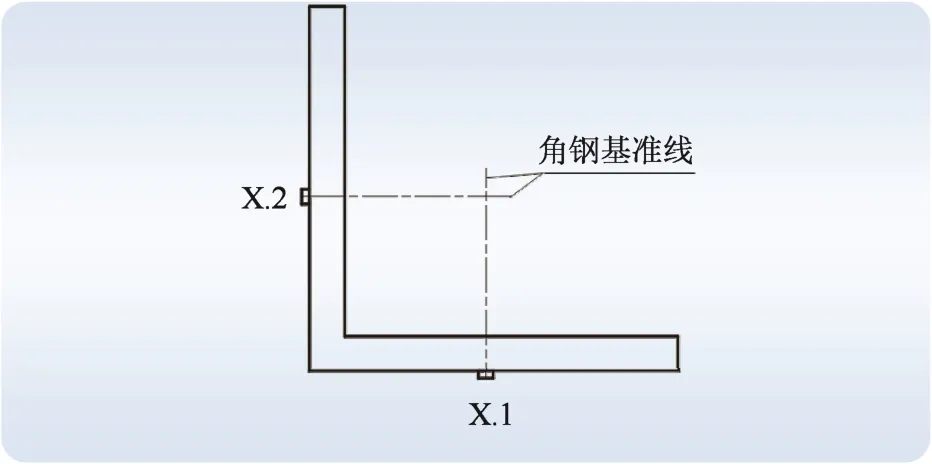
图1 双肢连接角钢贴片方式Fig.1 Location of the strain wafer of the double-limb connecting angle steel

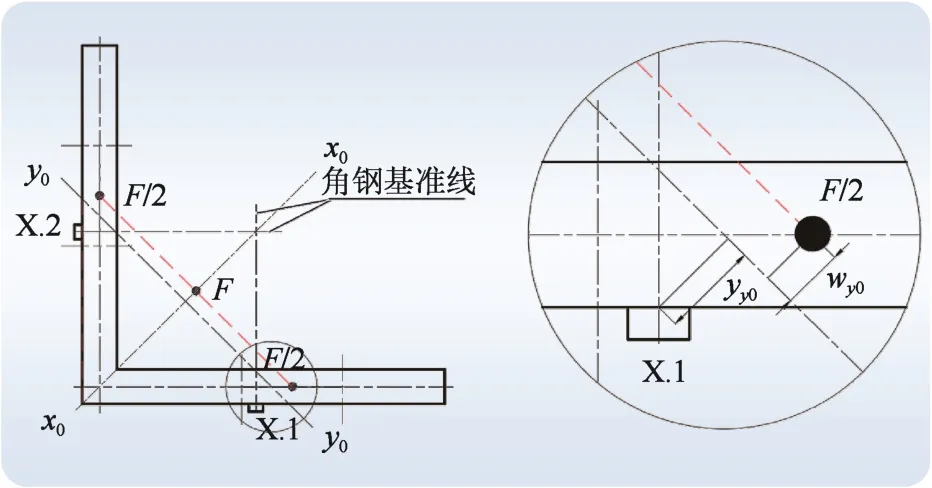
图2 双肢连接角钢截面参数示意图Fig.2 Schematic diagram (cross section) of the double-limb connecting angle steel

当角钢受到轴向力F且无附加弯矩影响时，整个角钢截面的应变为：

式中：F为受到的轴力；E材料的弹性模量；A为角钢横截面积。

如图2所示，由于力F不在两弯曲轴的交点上，因此在力F作用下产生绕y0-y0的附加弯矩，从而产生附加应变。此外，角钢两肢的贴片位置到y0-y0轴的距离相等，且在y0-y0轴的同一侧，所以应变1、2的值为：

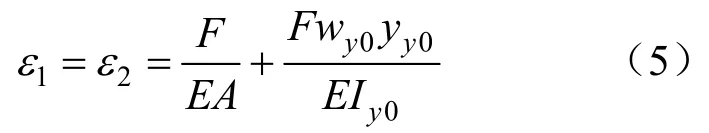
式中：wy0为力F对y0-y0轴的力臂。当F在y0-y0轴的左下方时，wy0为正；F在y0-y0轴的右上方时，wy0为负。yy0为应变片1到y0-y0轴的距离；Iy0为角钢的截面绕y0-y0轴的惯性矩。于是可得：

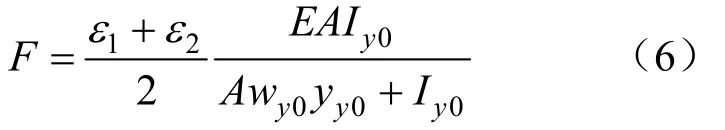
2 贴片误差对轴力测量结果的影响

将应变片的贴片误差分为应变片整体偏离（应变片主轴与角钢基准线平行）和应变片偏转（应变片主轴与基准线不平行）2类，如图3所示。

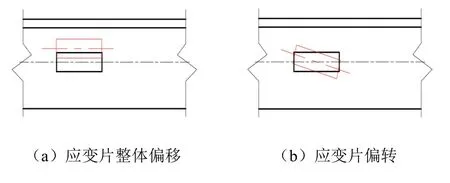
图3 应变片贴片误差类型Fig.3 Types of sticking error of strain wafer

2.1 应变片偏离对轴力测量结果的影响

由于偏心受力，角钢需要承受附加弯矩，造成同一截面各点的应力不相等。在实验过程中，若应变片偏离基准线，则利用应变读数按照轴力计算公式计算得到的轴力是存在一定的误差的。本文对双肢连接角钢进行建模，对模型施加一定的轴向力，然后提取角钢中部基准线两侧的应变值，研究应变片偏离基准线对轴力测量的影响。

选取某直线塔的横担主材进行分析。该主材型号为L140×12，长度为3.5 m。本文采用Workbench的DM建模环境进行角钢的建模。建模时，忽略角钢两肢端的倒角和轧弯处的圆弧，如图4所示。划分网格时，采用多域划分法，网格尺寸控制在4 mm。

图4 双肢连接角钢模型Fig.4 Model of the double-limb connecting angle steel

该段主材在某工况中的轴力大约为-50 kN。本文对模型右端的螺栓孔施加50 kN轴向压力，左端螺栓孔固定。提取角钢基准线中点两侧±4 mm的应变值，并通过式（6）计算出轴力，与施加的-50 kN载荷情况进行比较，如图5所示。

图5 应变片偏离导致的轴力误差Fig.5 Axial force error caused by deviation of strain wafer

由图5可知，在轴向力作用下，当2片应变片皆不发生偏移时，通过式（6）计算得到的双肢连接角钢轴力与实际施加的载荷一致，说明了公式的正确性；当应变片偏离基准线小于4 mm时，偏离对双肢连接角钢轴力测量的影响很小，最大误差仅为0.1%。

2.2 应变片偏转角度对轴力测量结果的影响

实验人员贴片失误导致应变片主轴发生偏转，则应变片主轴方向的应变不再是角钢轴向应变；并且由于横向效应的影响，应变片的读数也不是应变片主轴方向上的角钢的应变，因此：利用这时的应变读数进行轴力计算势必会造成误差的出现。

在贴片时，应变片5°～6°的偏转难以用肉眼辨别，因此选取偏离基准线±6°的方向上的应变进行分析。根据角钢的实际应变，通过式（3）计算出应变片的读数，再利用式（6）计算得到的轴力。计算结果与实际载荷进行比较，如图6所示。

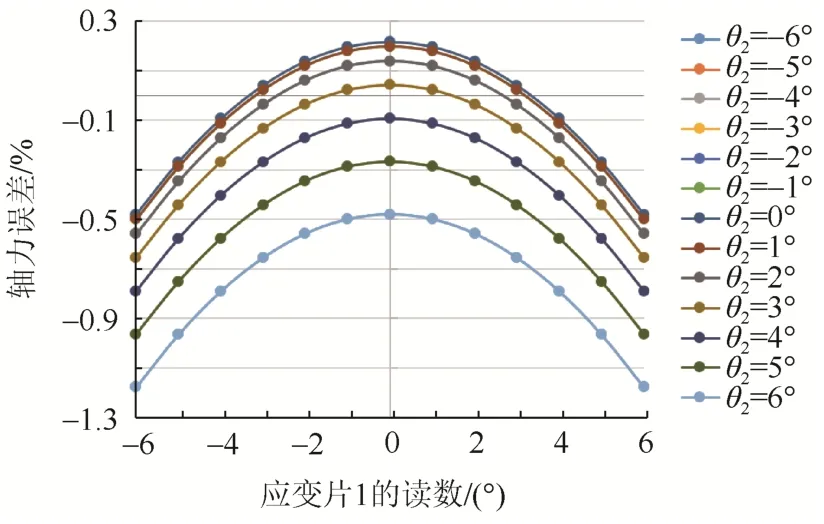
图6 应变片偏转导致的轴力误差Fig.6 Axial force error caused by strain wafer deflection

从图6可以看出：图中仅有7条曲线，其原因是θ2与-θ2的误差曲线完全重合；即当双肢连接角钢仅受轴向压力时，无论是向肢棱偏转还是向肢端偏转，相同偏转角度时应变片测量误差大小是相同的。当θ1=θ2=0°时，误差值为0；随着偏转角度得增大，误差绝对值也相应增大，最大仅为1.4%。这说明当角钢仅受轴向力作用时，应变片偏转小于6°对轴力测量的影响可以忽略。

3 扭矩对角钢轴力测量的影响

3.1 扭矩值的选取

首先计算出角钢所能承受的最大扭矩，然后将最大扭矩的10%加到角钢上。观察角钢同时受轴向力和扭转力作用时，应变片偏转对轴力测量的影响。

角钢为开口型薄壁杆件。根据高等材料力学中关于开口型薄壁杆件扭转问题的相关阐述，可将角钢截面分割为几个矩形，然后通过求解各个矩形截面得到的最大剪切应力，来寻求扭转时角钢截面上的最大剪应力值。矩形截面的最大剪应力与扭矩、矩形尺寸的关系式为：

单位长度的扭转角为：

式中：ai、bi分别为扭转截面的第i个矩形的长边和短边；Mi为第i个矩形上承受的扭矩；τmaxi代表第i个矩形长边中点附近的剪应力；G为材料的剪切模量；βi、β1i是与ai/bi有关的系数，其取值可参考表1。

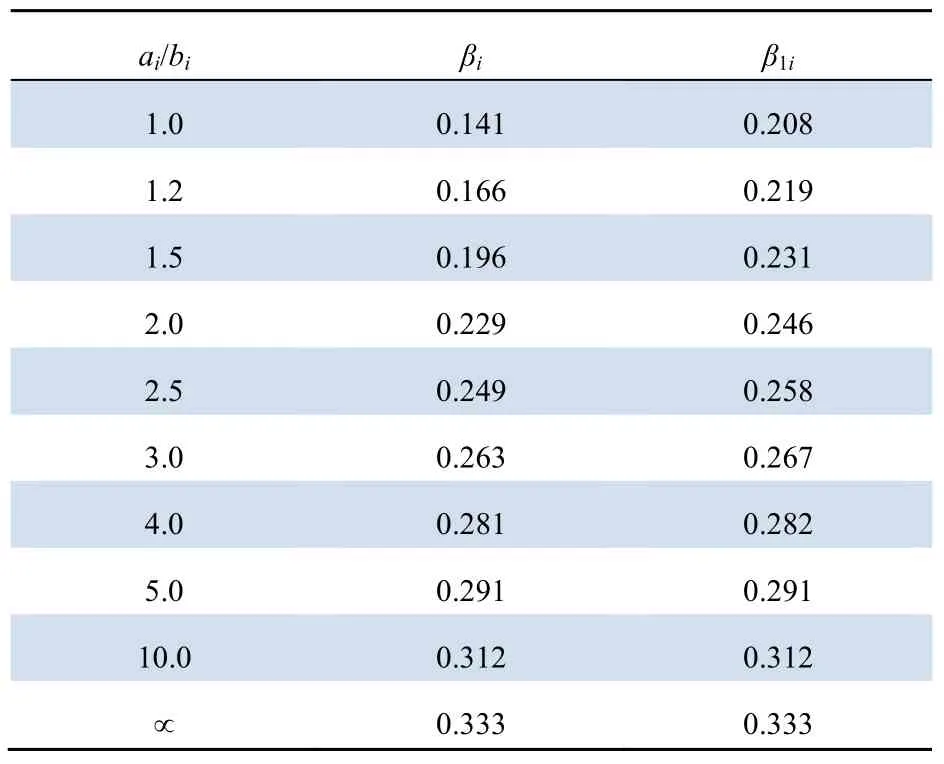
表1 βi、β1i的取值方法Tab.1 Selection of βi and β1i

由式（8）可知：

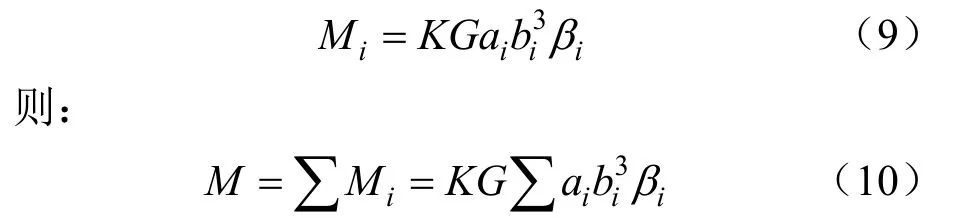
联立式（9）和式（10）得：

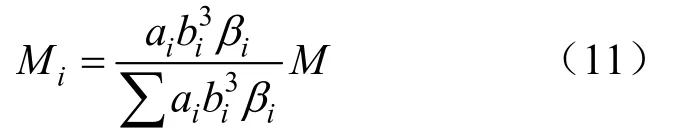
将式（11）代入式（7）得：

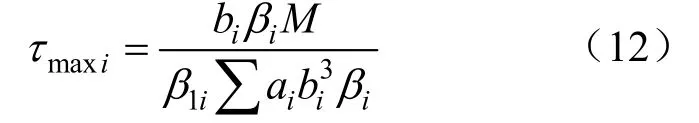
如图7所示，对L140×12的角钢进行分割。图7中，a1=140 mm，b1=12 mm，a2=128 mm，b1=12 mm，β1=β11=0.312，β2=β12=0.312。于是计算得：

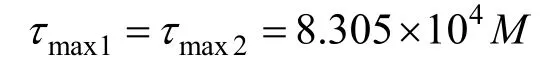
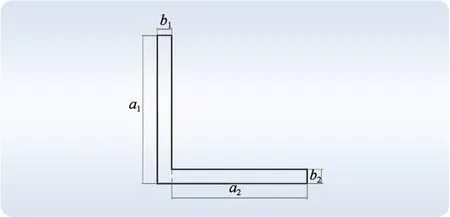
图7 角钢截面分割示意图Fig.7 Cross section view of angle steel

根据最大切应力理论，当最大切应力τmax达到材料单向拉伸屈服时得到最大切应力值τmaxs。当材料发生屈服，此时τmaxs=σs/2（σs为材料得屈服强度）。对于Q420材料，σs=420 MPa，即τmaxs=210 MPa。因此，τmax1、τmax2必须满足τmax1=τmax2＜τmaxs=210 MPa，于是可计算出角钢可承受最大扭矩为M=2 529 N·m。

3.2 扭矩对角钢轴力测量的影响

当角钢同时受到轴向压力和扭转力的作用时，角钢基准线上的单元受力状态变为平面应力状态，即正应力和切应力共同作用。这时，角钢轴线方向不再是最大主应力方向，基准线两侧的应变不再相等（仅受轴力时是相等的）。

将10%最大扭矩施加到角钢的右端面处，提取偏离基准线±6°的应变值，并将其换算成应变片的读数；利用轴力公式计算出轴力，并与所施加轴心载荷进行对比。对比结果如图8所示。

图8 压扭组合作用下的轴力误差Fig.8 Axial force error under compression and torsion combination

从图8可知：当存在扭转力时，计算得到的轴力误差并非是对称的。当θ1=θ2时，误差非常小，几乎接近于0。这说明，若2应变片的偏转方向和角度一致，则扭转力的存在对角钢轴力测量的影响极小。误差值与应变片偏转角度成线性关系。当θ1=-6°，θ2=6°时，误差值达到28.7%；当θ1=6°，θ2=-6°时，误差值达到31.5%。

为研究扭矩大小对轴力测量的影响，本文选取θ1=-6°时的情况。通过改变扭矩数值，研究扭矩大小对轴力测量的影响规律，结果如图9所示。

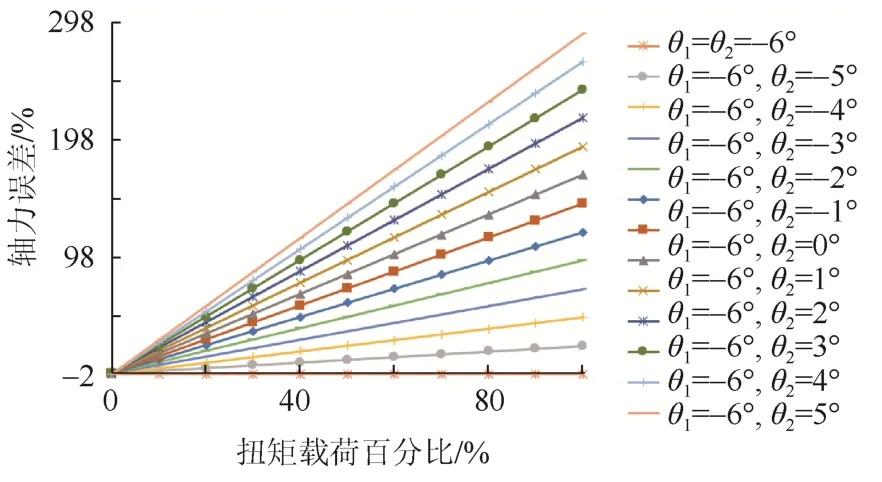
图9 θ1=-6°时轴力误差随扭矩的变化规律Fig.9 Variation of axial force error with torque when θ1= -6°

当θ1=θ2时，轴力误差值不随扭矩变化发生改变，且其值与仅受轴向压力作用时相同：说明当角钢两肢上的应变片偏转角度相同时，扭矩对轴力测量无影响。当θ1≠θ2时，轴力误差随扭矩的增大而增大，且误差与扭矩载荷大小成线性关系。当扭矩大小不变时，误差随θ2的增大而增大，这与前述中角钢同时承受一定的轴向力和扭矩时的变化规律是一致的。

4 结论

为分析了贴片误差和角钢扭矩对双肢连接角钢应变测量数据的影响，本文给出了用应变数据计算角钢轴力的计算公式；以规格为L140×12的双肢连接角钢为研究对象，进行了有限元仿真分析，得到以下结论。

（1）本文推导的由测量应变值计算双肢连接角钢轴力的公式是有效的。

（2）在轴向力作用下，当偏移距离小于等于4 mm时，应变片的整体偏移对本文所选角钢轴力的测量结果影响很小，误差最大仅为0.1%；当偏转角度小于等于6°时，应变片的偏转对本文所选角钢轴力的测量结果影响很小，最大误差为1.4%。

（3）当双肢连接角钢既承受轴力又承受扭矩作用时，若2应变片偏转角度不同，则会导致较大的误差出现；且随着扭矩的增大，误差值随其线性增加。对于本文所选角钢，当其承受 50 kN轴向力、10%最大扭矩以及θ1=6°，θ2= -6°时，误差值达到31.5%。

（4）通过本文研究发现：进行角钢力学性能实验时，若在载荷施加过程中角钢偶然出现较大的扭矩，势必会导致应变测量数据失真，进而造成较大的轴力误差，影响实验结果的准确性。