摆式惯容-零二次刚度自复位阻尼器并联加固双柱墩抗震性能研究

张振华， 张静思， 王 磊

(河南理工大学 土木工程学院，河南 焦作 454000)

钢筋混凝土(reinforced concrete，RC)双柱桥墩不仅能满足多车道的需求，还能提供较大的侧向抗力和抗倾覆力矩以控制结构侧向变形和上部结构倾覆，目前被广泛用作中小跨径公路桥和城市高架桥的下部结构。但对历次破坏性地震的统计结果表明，RC双柱墩在强震下易发生塑性铰区的弯、剪破坏和较大的残余变形[1-4]，非常不利于灾后救援和重建。因此，发展强震下结构损伤可控、震后功能可恢复的桥梁加固技术具有很强的现实意义。

目前基于保险丝理念的防屈曲约束支撑(buckling-restrained brace，BRB)和自复位支撑(self-centering brace，SCB)加固双柱墩技术已被研究证明能有效控制结构地震下的变形[3-12]。近期Dong等系统比较了SCB加固和BRB加固双柱/多柱墩的抗震性能和自复位能力，结果均表明SCB在残余位移控制方面具有更加显著的优势。但自复位加固双柱墩也带来一些不容忽视的问题。Dong等利用碟簧组作为自回复元件与传统BRB并联提出的自回复BRB(self-centering-buckling-restrained brace，SC-BRB)与普通的BRB相比，SC-BRB加固桥墩会导致上部结构峰值加速度和桥墩基底剪力的显著增加。Xiang等研究表明活塞式自复位支撑(piston-based self-centering damper，PBSCBs)加固双柱桥具有更好的自复位性能，但是加固结构对自复位支撑的最大恢复力需求明显高于BRB，这意味着PBSCB加固结构会导致更大的加速度和基底剪力响应。这是因为SCB恢复力需求的增加会显著增加结构的自振频率，从而使结构吸收更多的地震作用。过大基底剪力会增加墩柱发生剪切破坏的概率，因此有必要研究SCB加固双柱墩基底剪力和结构加速度的控制问题。Yousef-Beik等[13]提出了一种由摩擦元件和蝶簧构成的零二次刚度自复位阻尼器(zero-secondary-stiffness self-centering damper，ZSCD)来控制结构的峰值和残余位移，研究结果表明该阻尼器在有效控制结构峰值和残余位移的同时，并没有显著增加结构基底剪力。因此采用零二次刚度的自复位阻尼器加固结构，有利于控制自复位加固结构的基底剪力。

近年来，惯容类阻尼器在土木结构振动控制中的应用引起广泛关注[14], 惯容的调频作用可用来抵消由SCB添加导致的结构自振频率增加现象，进而可减小地震作用，可为解决自复位加固后结构加速度和基底剪力增加问题提供一种途径。在目前研究中，可通过对惯容、弹簧和阻尼器进行不同的组合构成不同的惯容减震(振)系统，包括惯容阻尼器(inerter damper，ID)[15-16]，调谐黏性质量阻尼器[17-18]和调谐惯容阻尼器[19-20]等。其中，ID是直接将惯容的两个节点与结构相连而不会引起结构的附加自由度，且这种连接方式能更直接地通过改变惯质的大小来调节结构的自振频率，进而抑制地震作用[21]。目前惯容主要的结构形式有滚珠丝杠式、齿轮齿条机构、液压式和电磁式等。这些惯容装置具有复杂精密的机械、电磁结构和传动关系，运维要求和成本较高，不易在桥梁工程中推广。

综上，现有的自复位阻尼器加固会导致双柱墩基底剪力和桥梁上部结构加速度显著增加，增大了墩柱的破坏风险。为了解决这一问题，作者提出一种由摆式惯容和零二次刚度自复位阻尼器并联构成的自复位阻尼系统(based inerter and zero-secondary-stiffness self-centering damper，IZSCD)来加固双柱墩。通过被加固结构位移反应谱的研究和直接基于位移的设计方法，对IZSCD加固双柱墩进行抗震设计，并通过弹塑性时程分析对设计结果进行验证和研究。结果表明，与SCD(self-centering dampers)和ZSCD加固双柱墩相比，所提出的IZSCD在控制自复位加固双柱墩桥的加速度和基底剪力方面有显著优势。该研究可为IZSCD加固双柱墩的抗震设计提供指导。

1 摆式惯容-零二次刚度自复位阻尼系统(IZSCD)

本研究提出的摆式惯容-零二次刚度自复位阻尼系统(IZSCD)如图1所示。由摆式惯容和零二次刚度自复位阻尼器并联组成。

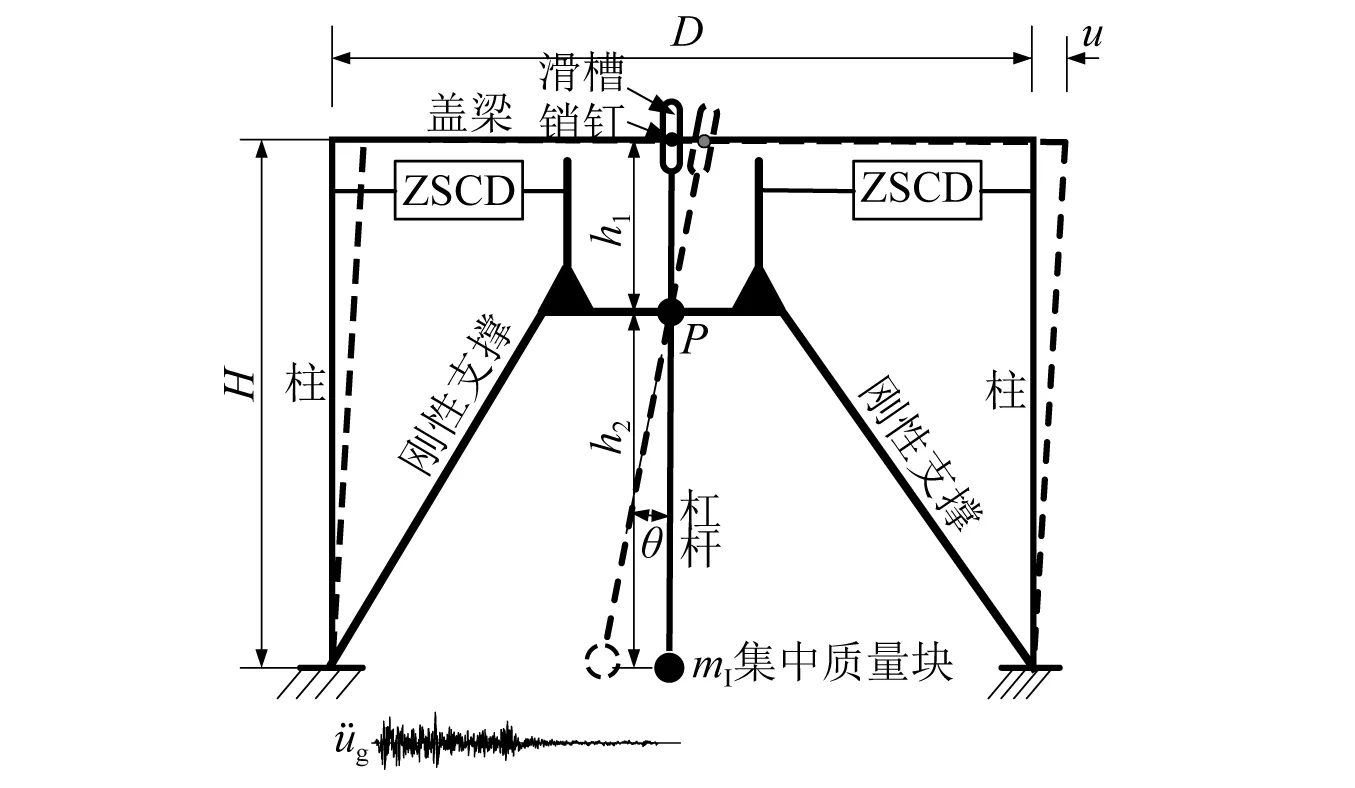
图1 IZSCD加固双柱墩结构简图Fig.1 Configuration of the double-column bridge bent retrofitted with IZSCD

PI由刚性支撑、杠杆和集中质量块mI组成，杠杆支点与刚性支撑铰接于P。杠杆的上端通过杠杆上的滑槽与盖梁上的销钉连接，杠杆下端安装一集中质量块mI。杠杆支点距盖梁距离为h1，距质量块距离为h2。当上部结构与地面产生水平相对运动时，盖梁通过销钉驱动杠杆，进而带动下部集中质量块进行摆动，使上部结构受到来自该摆的惯性阻力。该惯性阻力一方面可以增大结构表观质量，另一方面可以减小桥梁的地震作用。新提出的摆式惯容与现有的齿轮齿条和滚珠丝杠等惯容相比，具有更简单的结构形式，制造和维护成本较低，便于在土木工程中推广应用。

ZSCD由Yousef-Beik等提出，其结构如图2(a)所示，由自复位摩擦机构和受压蝶簧组成，详细结构见Yousef-Beik等的研究。该阻尼器不能受拉只能受压屈曲，其力-位移曲线如图2(b)所示，具有零二次刚度的自复位特征。如图1所示，当ZSCD在结构中对称安装时，ZSCD提供给结构的恢复力与变形的关系可用图2(c)所示的双旗帜滞回分段线性模型表示。图中的参数Fsy,usy,usu,Ks,α和β分别为屈服力、屈服变形、极限变形、初始刚度、屈服后刚度比和滞回因子。

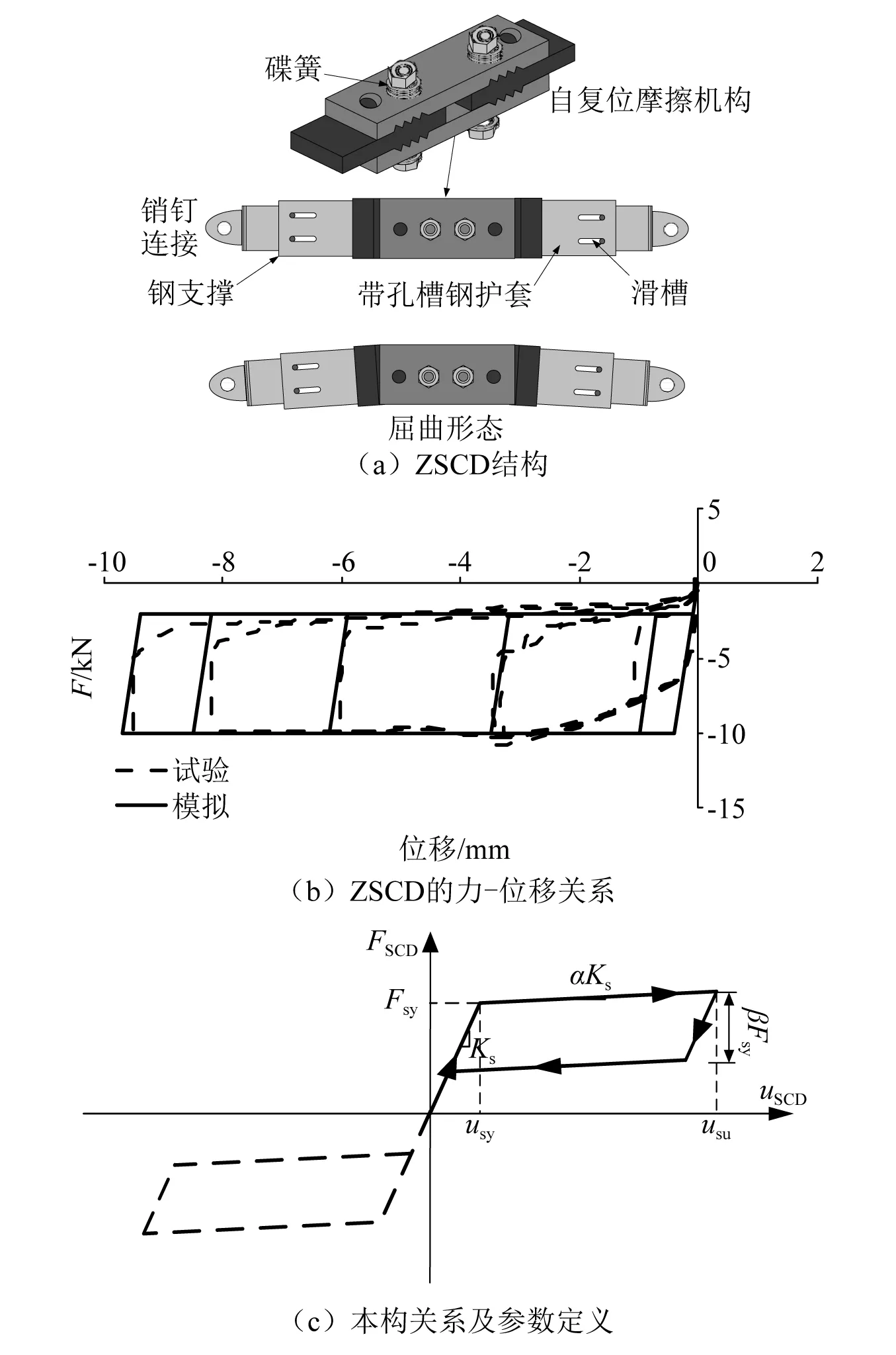
图2 ZSCD结构及分段线性本构关系Fig.2 ZSCD and its piecewise-linear constitutive model

杠杆受力分析如图3所示。对P点应用动量矩定理可得

(1)

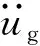
(2)

式中，φ为放大系数，φ=h2/h1。

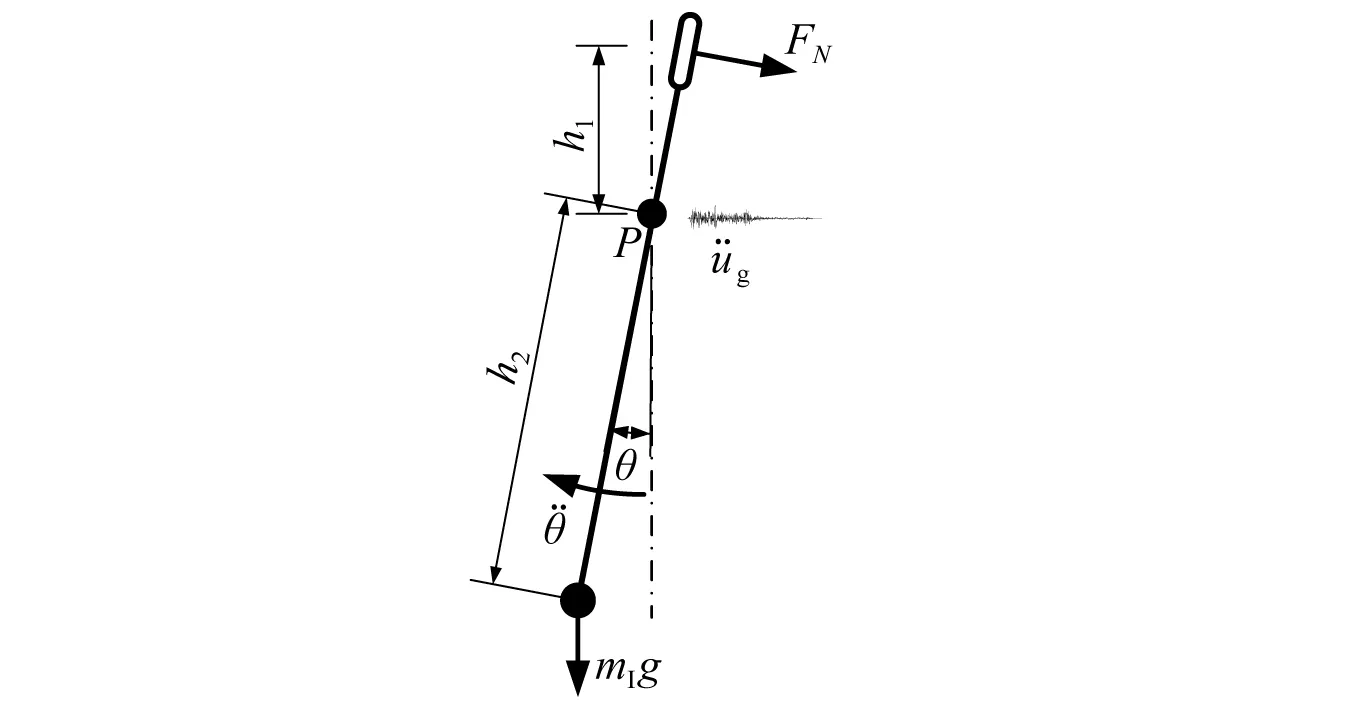
图3 IZSCD中杠杆的受力分析Fig.3 Force analysis of the lever in IZSCD

易知杠杆作用在帽梁上的力与FN互为反力。将地震作用下IZSCD加固双柱桥梁简化为如图4所示单自由度动力学模型，其动力学方程可写为

(3)

式中：M为双柱墩和上部结构的等效质量；C为桥梁内部阻尼系数；Fp(u)为原结构双柱墩的侧向抗力；FZSCD为ZSCD提供的阻尼力；MI=φ2mI为PI的表观质量。由方程式(3)可知，摆式惯容的增加不仅增加了结构的表观质量，延长了结构的自振周期，还抵消了部分地震激励。

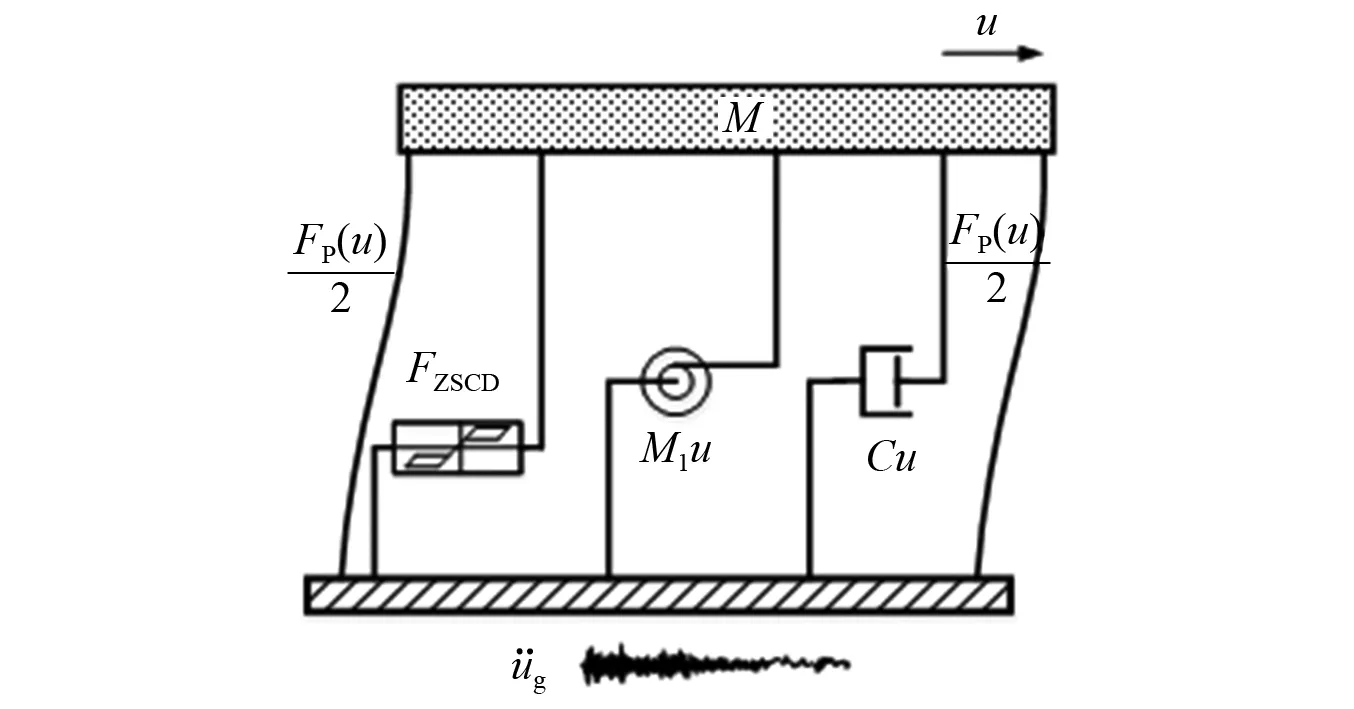
图4 IZSCD加固双柱墩单自由度模型Fig.4 Linearized SDOF model for double-column bridge bent retrofitted with ISCDS

2 IZSCD加固双柱墩抗震设计方法

2.1 位移反应谱

对动力学方程式(3)进行线性化等效，可得

(4)

式中：Ceq为等效阻尼系数；Keq为等效刚度。将动力学方程进一步无量纲化为

(5)

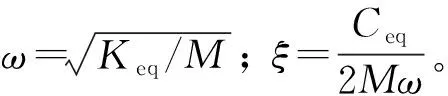
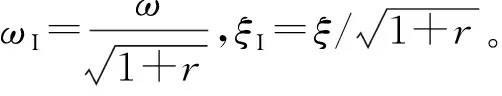
(6)

当惯容质量比r=0时，系统的加速度反应谱可表示为

(7)

根据方程式(6)和式(7)，位移反应谱和加速度反应谱关系表示为

(8)

式中，T=2π/ωI。

采用Eurocode 8标准加速度设计谱[23-24]表示Sa。将Sa代入式(8)可得含惯容线性化系统位移设计谱。

通过直接积分法求解方程式(5)，获得地震作用下含惯容系统的位移反应谱，并和式(8)得到的位移设计谱进行比较，以验证该位移设计谱。地震作用下的位移反应谱计算步骤如下首先根据场地类型和设计地震加速度确定普通线性系统加速度设计谱；通过该加速度设计谱，在PEER(太平洋地震工程研究中心)数据库[25]中选取地震波；用SeismoMatch软件对所选地震波与加速度设计谱进行匹配[26-27]；给定惯质比，通过直接积分法求解方程式(5)，获取不同自振周期系统的位移极值，绘制自振周期与位移极值之间的关系，得到含惯容线性化系统的位移反应谱。

以C类场地为例，设计地震加速度取0.4g，等效阻尼比取5%。根据加速度设计谱选择10条地震波，其基本信息如表1所示。根据上述流程，计算得到含惯容线性化系统地震作用下的位移反应谱，并与对应的位移设计谱进行比较，如图(5)所示。图5中的平均位移反应谱是指10条地震动下位移反应谱的平均值。结果表明，在自振周期小于2 s内，平均位移反应谱和位移设计谱吻合较好，说明所提出的位移设计谱可较好地预测具有中低自振周期含惯容线性系统的位移。此外，在结构自振周期相同时，谱位移随着惯质比的增大而减小，说明惯容对系统位移响应具有较好的抑制作用。本文拟基于该位移设计谱，采用直接基于位移(direct displacement-based design,DDBD)方法对IZSCD加固双柱墩进行抗震设计。

表1 选定地震动信息Tab.1 Information of the selected ground motions

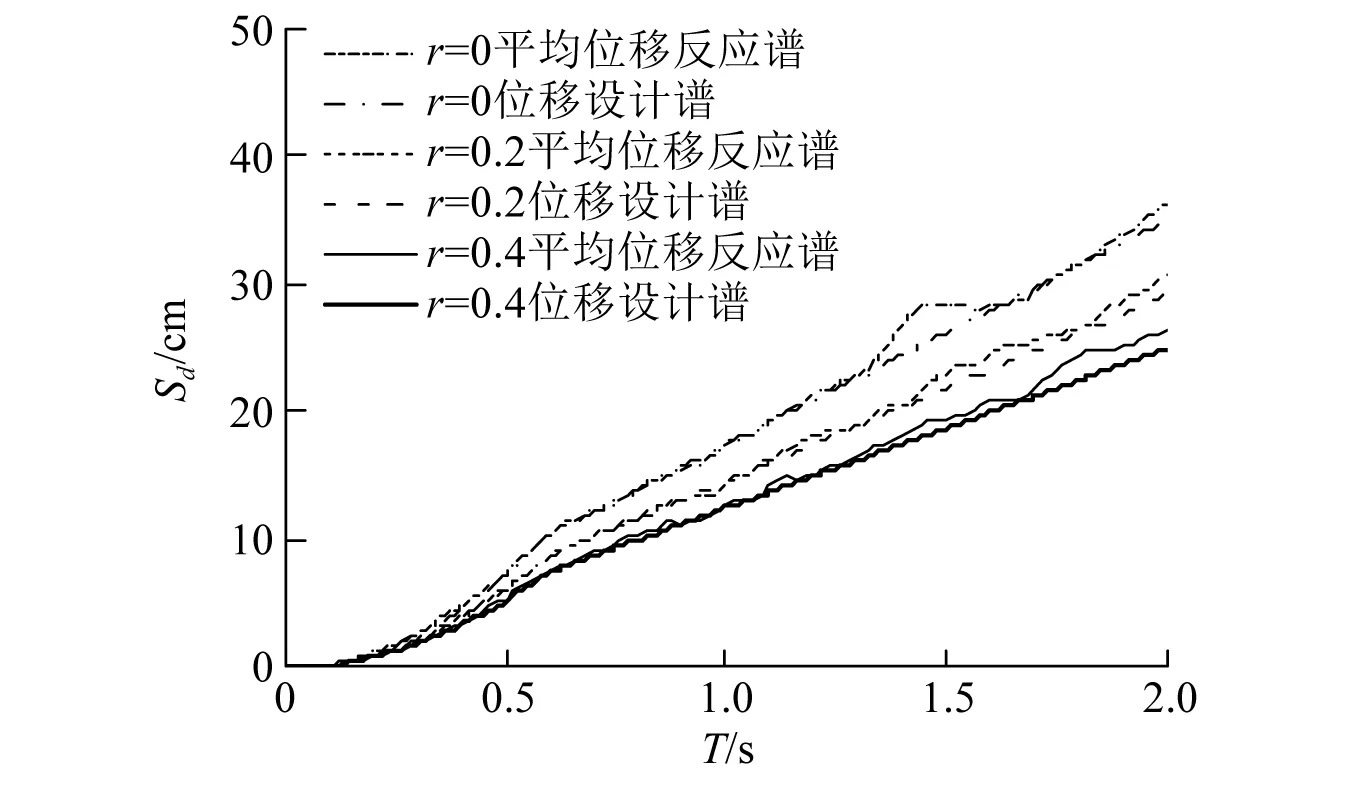
图5 位移设计谱验证Fig.5 Validation of the proposed displacement design spectrum

2.2 IZSCD加固双柱墩DDBD流程

基于2.1节中提出的位移设计谱，利用Priestley等[28-29]提出的直接基于位移的设计流程(DDBD)，提出IZSCD双柱墩加固设计流程如下。

步骤1通过原始双柱墩的Pushover分析，确定原始双柱墩的屈服力Fpy, 屈服位移upy，极限位移upu和极限力Fpu。

步骤2在设计地震动下，确定加固双柱墩的设计位移ud，为了确保桥梁在设防地震下处于弹性状态，阻尼器应先于双柱墩屈服，使ud≤upy。

步骤3由几何关系知，阻尼器ZSCD的设计变形uZ=ud。设ZSCD的位移延性为μs，放大系数为φ，惯容质量比为r，则ZSCD的屈服变形可表示为usy=uZ/μs。

步骤4假设ZSCD的初始屈服力为Fsy，则ZSCD的初始刚度Ks可表示为

Ks=Fsy/usy

(9)

步骤5ZSCD的最大力Fsu可表示为

Fsu=Fsy+(usu-usy)αKs=Fsy

(10)

步骤6加固双柱墩的等效刚度Ke可表示为

Ke=(Fsu+Fpy)/ud

(11)

步骤7加固双柱墩的有效质量me和有效周期Te表示为

(12)

(13)

式中：msup为双柱墩上部结构的质量；msub为下部结构质量；MI为惯容的表观质量。

步骤8加固双柱墩整体系统的等效黏滞阻尼比ξ可表示为

(14)

式中：ξs为ZSCD的等效黏滞阻尼比；ξp为原始双柱墩的等效黏滞阻尼比。表示如下

(15)

(16)

式中：β为ZSCD的滞回因子；μ为原始双柱墩的位移延性。

步骤9根据式(17)计算阻尼修正系数，和场地类型参数和设计地震加速度共同代入式(8)获得位移设计谱。将有效周期Te代入该位移设计谱，计算出谱位移Sd。

(17)

步骤10检查谱位移Sd=ud是否成立。若不成立，返回步骤4，重新迭代；如满足，停止迭代，完成设计。

步骤11根据获得的参数设计阻尼器。

整个设计DDBD流程如图6所示。

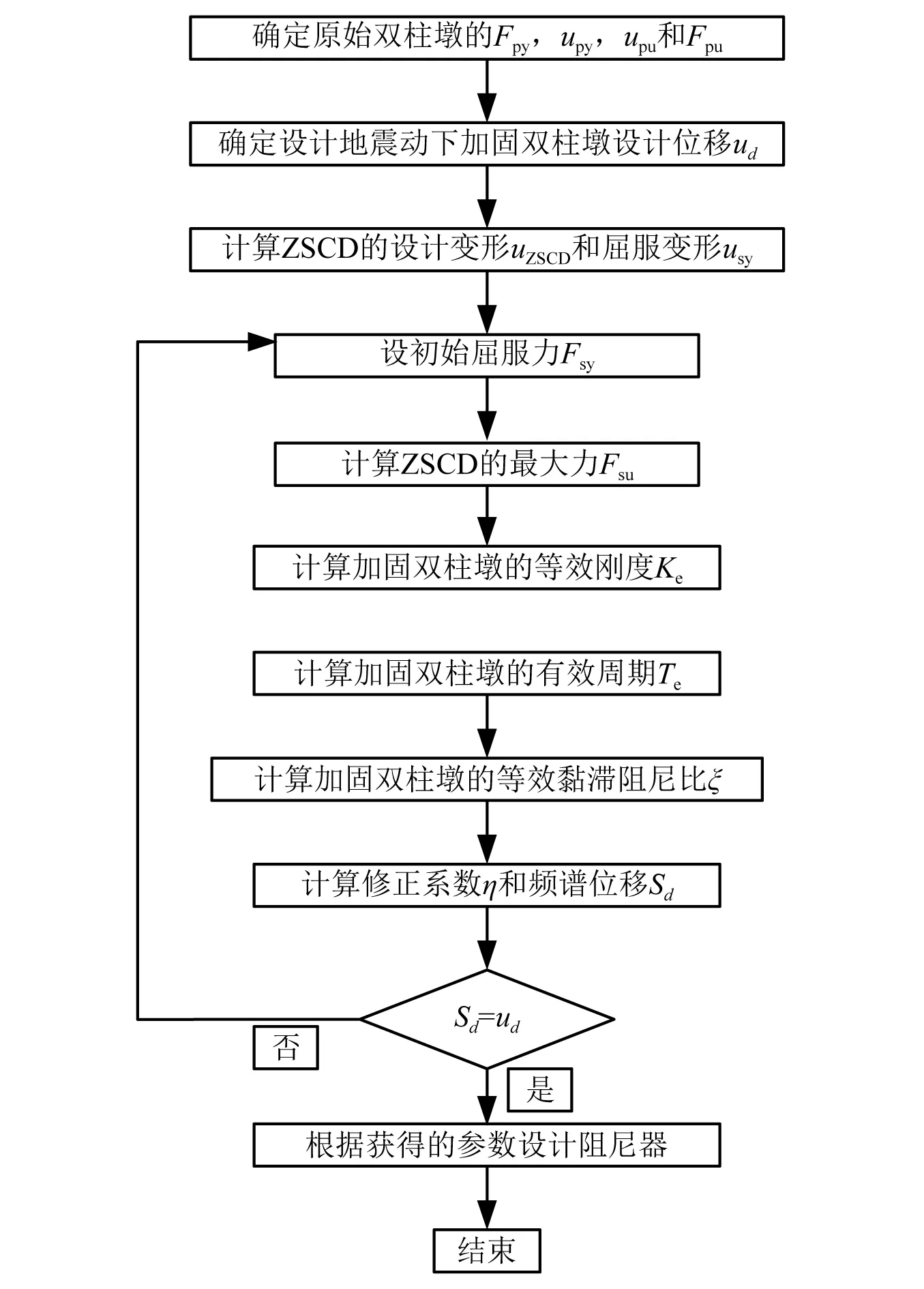
图6 IZSCD加固双柱墩的DDBD流程Fig.6 DDBD procedure for double-column bridge bent retrofitted with IZSCD

3 设计实例

为了验证IZSCD加固双柱墩DDBD流程，本章选用一座三跨连续桥梁的混凝土双柱墩为加固对象进行抗震设计。该双柱墩结构和尺寸如图7所示。其由两根横截面为圆形的墩柱和横截面为矩形的盖梁组成。柱直径为1.6 m，净高7 m；盖梁长、宽、高分别为11.4 m，1.8 m，1.6 m。柱截面均匀分布有28Φ30 mm的纵向钢筋，配筋率为1.12%。钢筋屈服强度为400 MPa，混凝土的峰值强度为30 MPa。双柱墩的上部结构有效质量为942 t，下部桥柱质量为64 t。

图7 钢筋混凝土双柱墩原型(mm)Fig.7 Prototype of the double-column bridge bent (mm)

对原双柱墩进行Pushover分析得到其力学性能参数：Fpy=3 650 kN，upy=22 mm，upu=140 mm。根据DDBD流程，对IZSCD加固双柱墩进行抗震设计，为了便于比较，又分别对常规SCD和ZSCD加固双柱墩桥进行同位移目标的抗震设计。其中SCD可由不同自复位元件实现，比如蝶簧-摩擦复合自复位阻尼器和形状记忆合金基自复位阻尼器[30]等。

3种加固结构的设计参数如表2所示。该设计结果表明IZSCD加固结构中所需的阻尼器屈服力Fsy最小，是ZSCD加固结构中阻尼器屈服力的62%。并且IZSCD加固结构具有最大的等效自振周期。

为了验证设计结果，利用OpenSees软件对原桥墩和3种加固桥墩进行弹塑性时程分析。加固结构的有限元模型如图8所示。在该有限元模型中，桥梁上部结构等效为在盖梁顶部的集中质量。盖梁在历次地震的破坏并不显著，因此可采用弹性梁单元模拟。柱采用非线性纤维单元模拟。该类单元可以定义和组合不同的纤维来模拟约束混凝土、非约束混凝土和纵向钢筋，其可更好的模拟钢筋混凝土柱的弹塑性行为。自复位阻尼器采用Self Centering材料构成的两节点连接单元进行模拟，该单元可以很好的模拟ZSCD阻尼器的力-位移关系。摆式惯容中的杠杆和刚性支撑通过较高刚度的弹性单元模拟；杠杆与盖梁之间的滑槽-销钉连接可通过零长度弹性单元模拟，在该单元水平方向上设置较高刚度用于约束横向的相对位移，在垂向不设置刚度可模拟滑槽和销钉的相对滑动；杠杆支点与刚性支撑之间通过RigidLink命令进行约束，该约束限制其相对移动而不限制其相对转动。

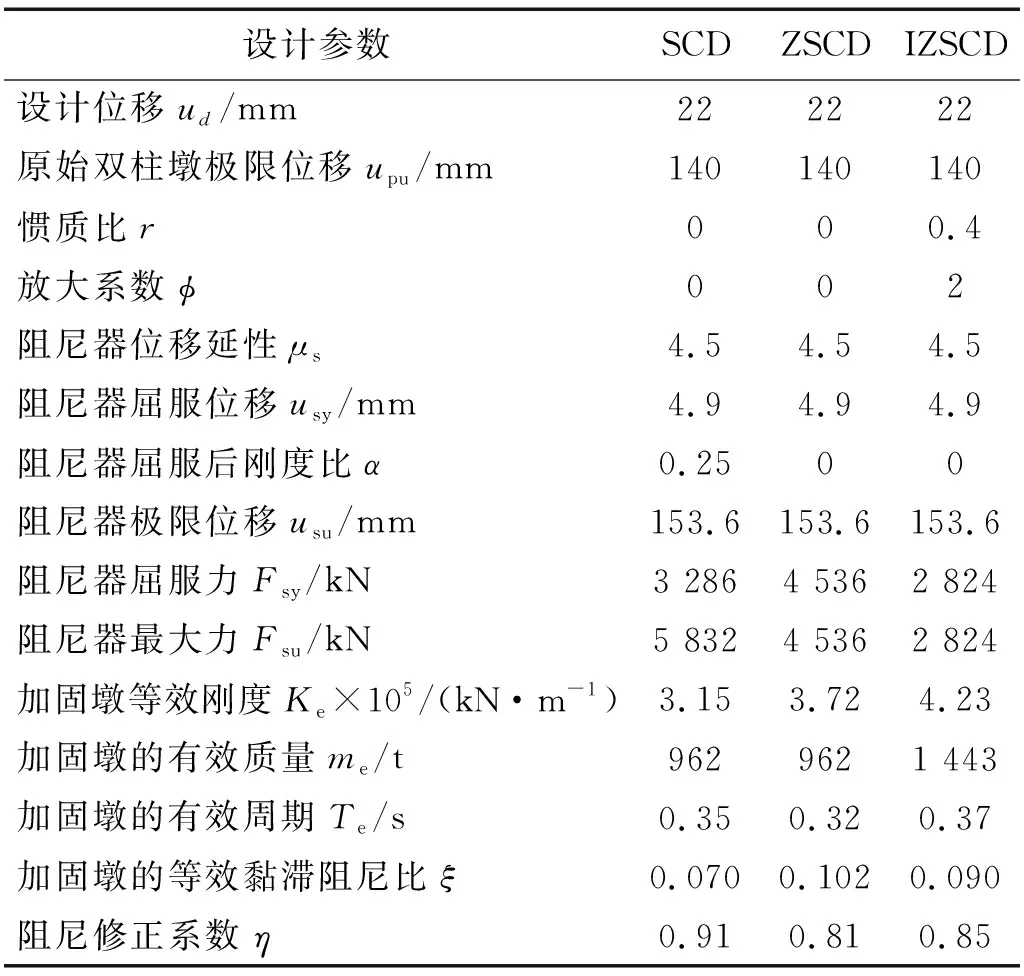
表2 SCD，ZSCD和IZSCD加固双柱墩的设计结果Tab.2 Design parameters of the bridge bent retrofitted with SCD, ZSCD and IZSCD respectively

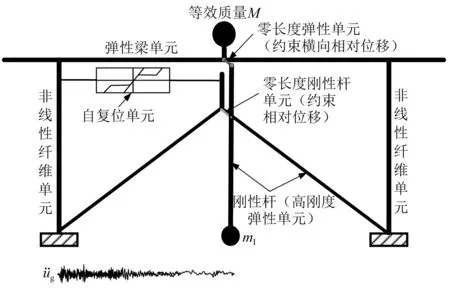
图8 IZSCD加固双柱墩有限元模型Fig.8 Finite model of the bridge bent with IZSCD

选用表1中10条地震波，并经过SeismoMatch匹配后作为结构弹塑性时程分析的地震激励。原结构和3种加固结构峰值位移、峰值加速度、基底剪力和残余位移等地震响应对比，如图9所示。图9(a)表明，3种加固双柱墩的上部结构峰值位移均能达到目标位移，证明了所提出IZSCD加固双柱墩桥的DDBD流程是可靠的。图9(b)表明，采用SCD，ZSCD和IZSCD加固结构的残余位移均远小于原结构，均表现出优异的自复位性能。

图9(c)表明，SCD双柱墩的峰值加速度明显高于原结构，而ZSCD加固结构的峰值加速度稍低于SCD加固结构，但仍明显高于原结构。而IZSCD加固结构的加速度明显小于原结构，其平均加速度是原结构平均加速度的64%。这表明单独的SCD或ZSCD会放大双柱墩桥的加速度响应，而IZSCD通过摆式惯容能有效降低双柱墩桥的加速度响应。

图9(d)表明，采用SCD，ZSCD和IZSCD加固双柱墩桥的基底剪力都高于原结构，而IZSCD加固双柱墩的基底剪力明显小于SCD和ZSCD加固结构，这表明PI系统的加入能有效减小地震作用下自复位阻尼器对基底剪力的不利影响。

总之，设计后的SCD，ZSCD和IZSCD加固双柱墩桥的弹塑性时程分析表明，三者均能达到设计位移目标和理想的自复位性能。与SCD和ZSCD相比，IZSCD能有效减小自复位加固对双柱墩加速度和基底剪力的不利影响。

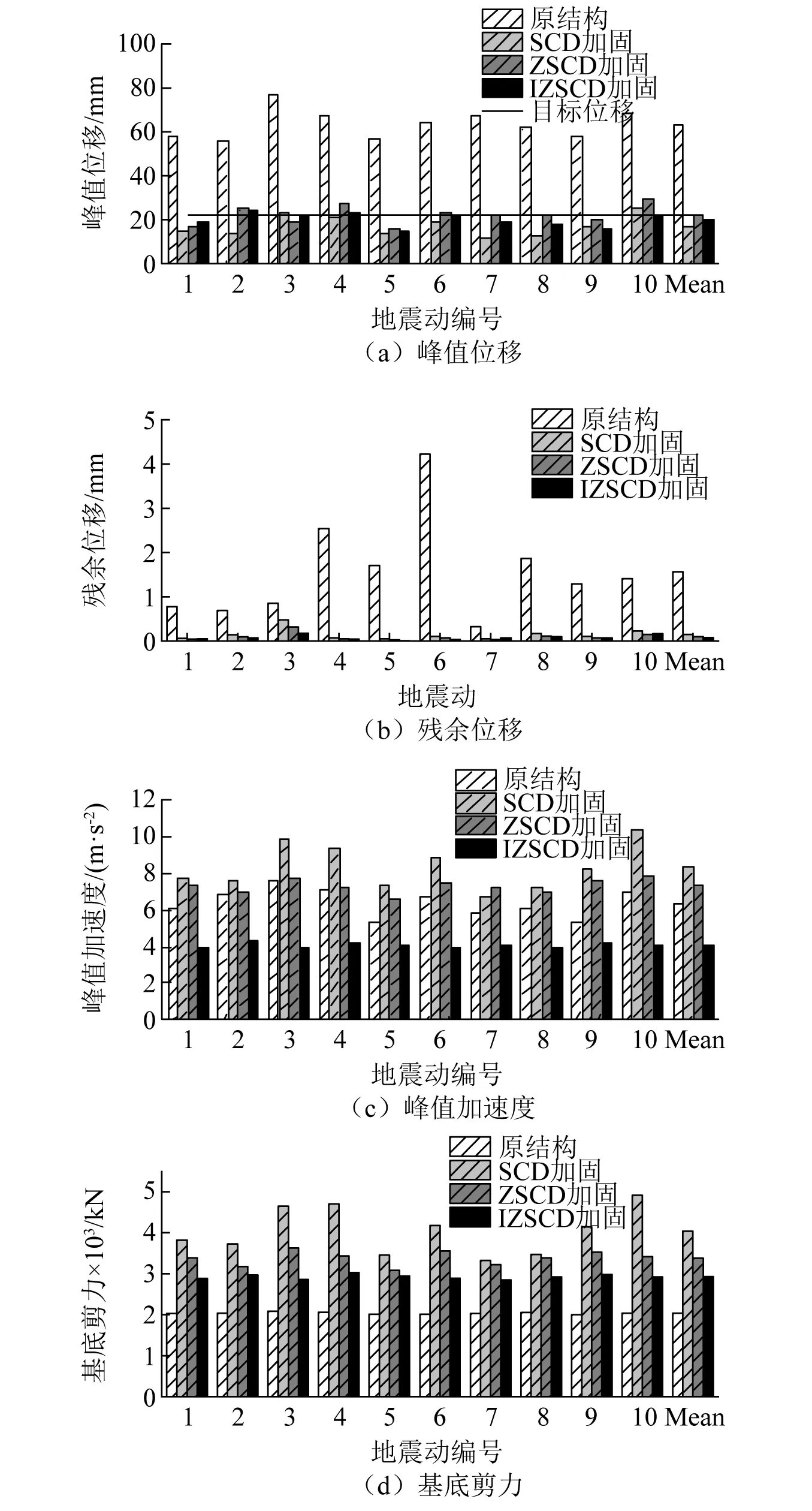
图9 原结构和加固结构地震响应对比Fig.9 Seismic responses compassion among the prototype and the structures with SCD, ZSCD and IZSCD respectively

图10比较了4种结构在地震Morgan Hill作用下结构基底剪力-位移滞回曲线和3种阻尼系统的恢复力-位移滞回曲线。图10(a)表明加固双柱墩桥的基底剪力高于原结构，而IZSCD有效降低自复位加固引起的桥墩基底剪力增量。图10(b)显示IZSCD作用于结构的最大恢复力最小。需要指出，IZSCD加固双柱墩和IZSCD的滞回曲线均比较复杂，这是由惯容与相对加速度线性相关性导致的。

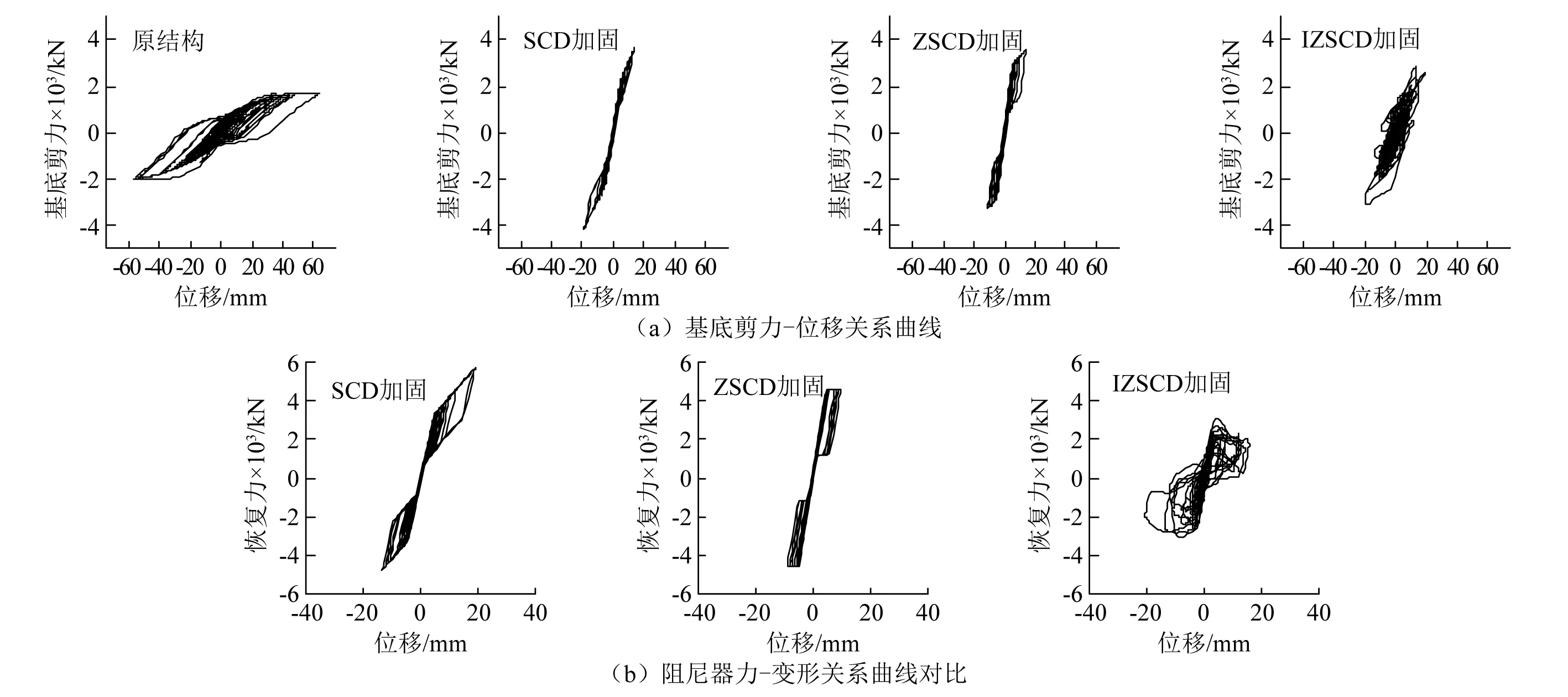
图10 原结构和加固结构在Morgan Hill地震动下滞回行为Fig.10 Hysteretic behaviors of the prototype and the three retrofitted structures

4 参数分析

4.1 惯质比

第3章的研究表明，在相同的目标位移下，IZSCD在控制自复位加固双柱墩的加速度和基底剪力方面有明显优势。为了进一步揭示惯容的影响，利用DDBD设计流程对不同惯质比的IZSCD加固桥梁进行抗震设计，并对设计结果进行弹塑性时程分析。惯质比r对IZSCD加固双柱墩桥的峰值位移、峰值加速度、基底剪力和残余位移的影响如图11所示。

图11(a)和(b)表明，含不同惯质比r的IZSCD加固双柱墩均能达到设计目标位移，且残余位移均远小于原结构的残余位移。图11(c)表明，随着惯质比r的增大，加固双柱墩桥的加速度响应逐渐降低。当r>0.2时，加固结构的加速度开始小于原始桥梁。当r=0.5时，加固结构的加速度与原结构相比，降低了36%。图11(d)显示，IZSCD加固后双柱墩基底剪力均高于原结构，但随着惯质比r的增加，双柱墩的基底剪力显著减小，r=0.5时的基底剪力是r=0.1时基底剪力的50%。表明惯质比r的增加能显著降低自复位加固对桥墩基底剪力和上部结构加速度的不利影响。但当r接近0.5时，加速度和基底剪力降低的速率明显减小。为了兼顾杠杆惯容的轻量化需求，建议r取0.5。

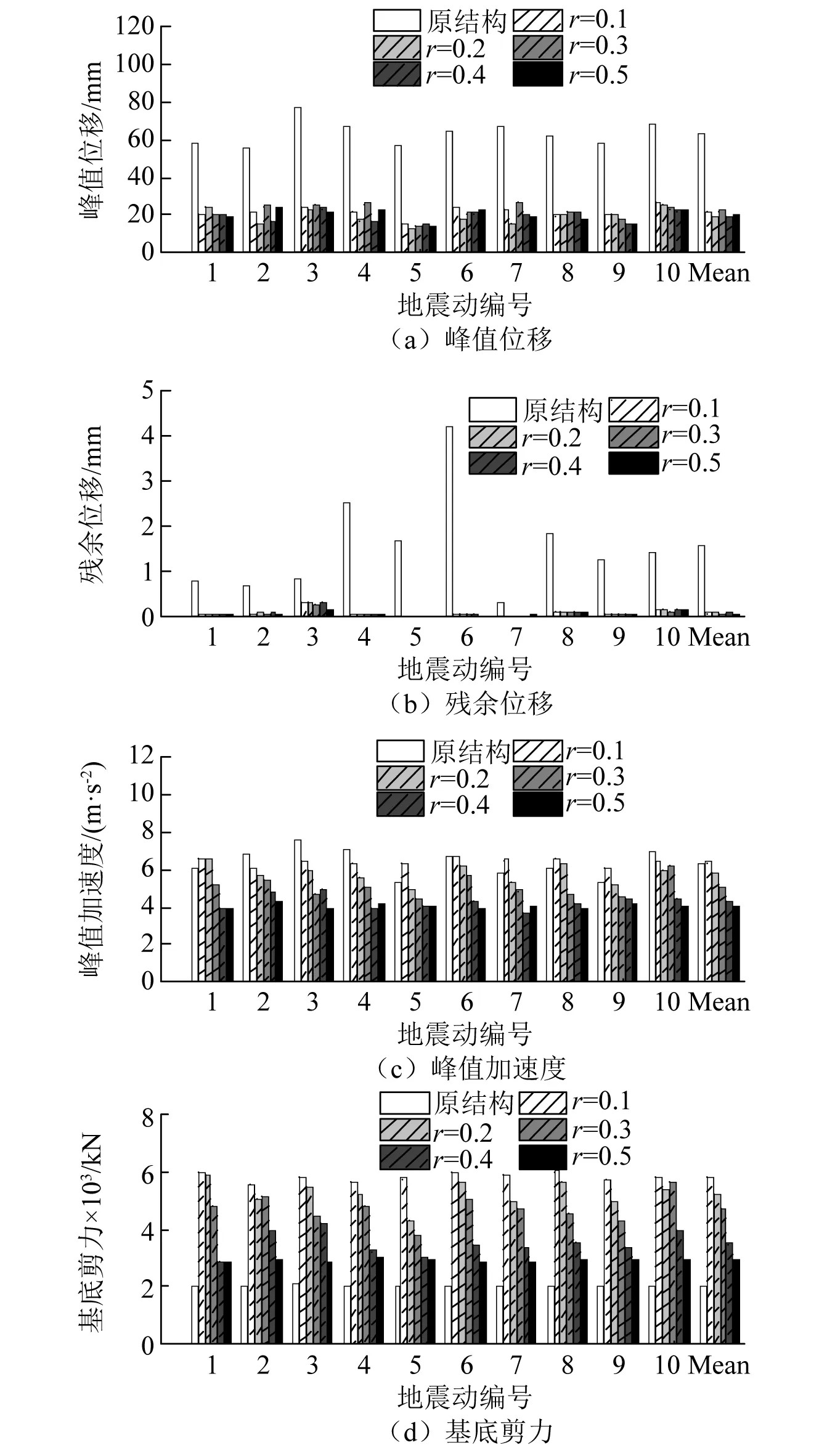
图11 惯质比r对IZSCD加固桥梁地震响应的影响Fig.11 Effects of r on the responses of bridge bent with IZSCD

4.2 杠杆放大系数

当r取0.5时，对不同杠杆放大系数φ的IZSCD加固双柱墩进行同目标位移的抗震设计，并对设计后的加固结构进行弹塑性时程分析。图12给出了不同φ时的IZSCD加固双柱墩的峰值加速度和基底剪力。结果表明，随φ的增加，IZSCD加固结构的加速度和基底剪力均先降低后增加，当φ=3时加速度和基底剪力均取最小值。因此，当φ=3时IZSCD对双柱墩加速度和基底剪力的控制效果最好。

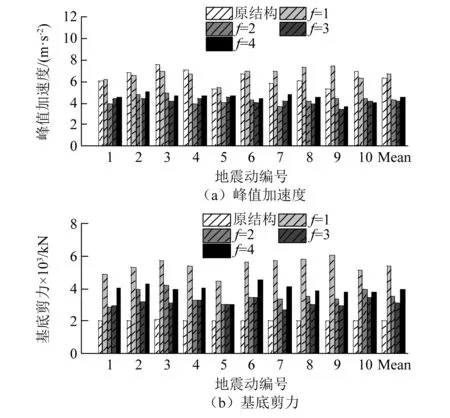
图12 放大系数φ对IZSCD加固桥梁地震响应的影响Fig.12 Effects of φ on the responses of bridge bent with IZSCD

此外，在实际应用时，既需要该摆式惯容系统能达到较好的减震效果，也希望该系统尽可能轻量化。根据r=MI/M和MI=φ2mI，可知r=φ2mI/M。定义rm=mI/M来表示附加质量块的物理质量与双柱墩桥等效质量之比，易知rm=r/φ2。当选定惯质比r时，希望得到较小的rm以减小附加物理质量。如图13所示，当r=0.5时rm随φ增大而减小，且当φ>3时rm减小的速率明显减缓，而再增大φ时就会需要更大的空间来安装IZSCD。综合考虑IZSCD的减震效果、轻量化和安装空间需求，建议φ=3。

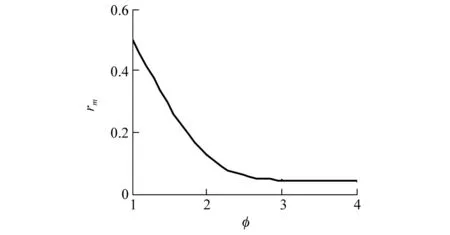
图13 rm和φ的关系Fig.13 Relationship between rm and φ

5 结 论

提出了一种新型的摆式惯容-零二次刚度自复位复合阻尼系统(IZSCD)用于加固双柱墩以控制自复位加固时双柱墩的基底剪力和上部结构的加速度响应。结合卷积积分和现有加速度设计谱提出含惯容单自由度线性化系统的位移设计谱，并通过对该系统的时程分析验证了该位移设计谱。基于所提出的位移设计谱，采用直接基于位移的设计方法对IZSCD加固双柱墩进行抗震设计，同时对SCD和ZSCD加固双柱墩也进行了同目标位移下的抗震设计，并利用弹塑性时程分析验证了设计结果。通过3种加固结构对比发现，IZSCD能有效减轻自复位加固对双柱墩桥加速度和基底剪力的不利影响。且在相同的设计目标位移下，增加惯质比有利于减小双柱墩的加速度和基底剪力响应，但减小速率随惯质比的增加而降低。此外，随着杠杆放大系数的增加，IZSCD加固双柱墩基底剪力和峰值加速度先减小再增大。综合考虑IZSCD的减震性能、安装空间及轻量化需求，建议惯质比取0.5，放大系数取3。

与现有双柱墩自复位加固体系相比，PI-ZSCD加固体系主要增加了摆式惯容PI。PI中的刚性支撑、摆杆和摆锤结构简单，且均由型钢构成，因此增加的成本是有限的，有望在双柱墩桥梁加固中推广使用。本文采用的设计方法虽然具有较多的设计步骤，但是设计思路清楚，在工程中应用时可通过编写迭代程序来实现双柱墩PI-ZSCD加固设计计算。