基于深度Q网络的轨道交通客流控制

张 辉，郭建媛，豆 飞，唐雨昕，杜佳敏

（1. 北京交通大学交通运输学院，北京 100044；2. 北京地铁运营有限公司，北京 100044）

城市轨道交通因具有方便准时等优点，吸引和承载了大量乘客的交通出行，这使得车站经常出现大客流聚集的情况。尤其是在高峰时段，当有限的线路运输能力不能及时满足出行需求时，许多乘客会聚集在站台上无法上车，如果在站台等候的乘客数量超过了站台的设计容纳人数，那么车站将会产生运营安全隐患。因此，在早晚高峰时期，对客流常采取控制措施，以缓解车站的客流压力。

近年来，国内外许多学者对轨道交通车站客流控制问题进行了研究。姜曼以城市轨道交通单线多站系统为研究对象，采取结合客流需求管理的运力资源配置方法，研究了拥挤客流的控制问题[1]。李登辉等以乘客总等待时间最少和客运周转量最大为目标，建立了线路客流协同控制线性规划模型[2]。赵鹏等以乘客延误损失最小化和客运周转量最大化为优化目标，利用所求解的控流率为限流措施，制定提供量化的依据[3]。Shi 等以特定线网下各车站乘客等待时间和风险总和最小化为目标，建立了一个双目标整数线性规划模型，用来描述乘客控制过程[4]。Li 等以最小化地铁线路的时刻表和发车间隔偏差为目标，建立了针对车站每列车的出发时间和载客量演变的耦合状态空间模型[5]。Zhang 等将列车运行和乘客上下车过程作为约束，以乘客总出行时间最小为目标，建立了非线性非凸规划模型[6]。

同时，从模型构建上可以分为线性规划模型[2-4]、二次规划模型[5]和非线性组合优化模型[6]。非线性组合优化客流控制模型能够更充分地刻画优化的安全和效率目标，对此传统的运筹学方法无法在短时间内做出动态决策。

为此，有学者尝试使用强化学习的方式进行客流控制优化求解。Jiang 等以最小化地铁车站乘客的滞留次数和候车时间为目标，提出基于强化学习方法来优化每个车站一定时间内的进站量，得到了比较好的优化效果[7]。另外，他们又以全线乘客滞留的惩罚值最小为目标，提出了将协调客流控制与列车重调度策略相结合的线路优化方案[8]。

综上所述，一方面，在目前的研究中，客流控制以提高乘客出行效率为主要的模型优化目标，相对较少考虑过多客流控制对乘客出行造成的不便，而过度的客流控制会增加乘客的等待时间，影响乘客的出行效率；另一方面，强化学习在客流控制问题上仅有初次尝试，还具有很大的研究空间。 因此，笔者建立了多目标多站客流协调控制模型，目的是在满足列车容量约束下，最小化地铁车站乘客的站台超限量、平均等待时间，提高客流控制强度的综合效益；并基于强化学习深度Q 网络，优化每个车站在一定时间内的进站量，以缓解车站站台的乘客拥堵，保障乘客的出行效率。

1 客流协调控制模型建立

1.1 模型假设

为构建模型，对相关影响因素作如下假设：

1) 列车按运行计划开行，不存在晚点。

2) 控制乘客进站，不会导致高峰期乘客出行需求减少。

3) 在地铁线路上，各车站可实施乘客进站控制策略。

4) 乘客遵循先到先上的原则。

1.2 目标函数

相关的参数以及所用变量在表1 中列出，目标函数如下：

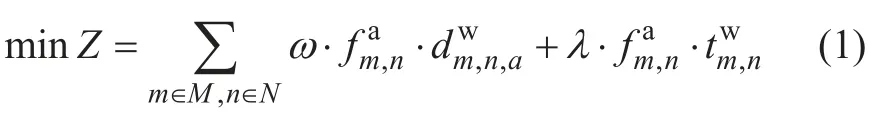
模型目标是在客流控制强度较小时，尽量减少乘客在站台等待的超限数及等待时间。

约束条件如下：

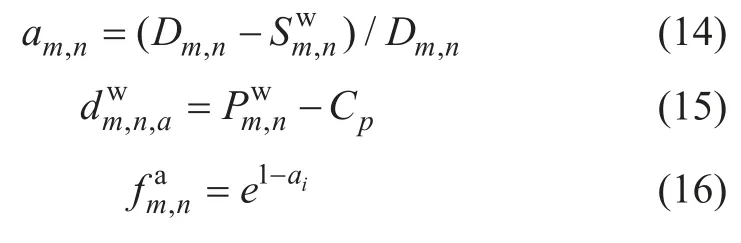
表1 变量及参数定义 Table 1 Definition of variables and parameters

式(2)表示到达站台时间等于乘客到达站外时间与站外等候时间以及站内走行时间之和；式(3)表示站台等待时间等于登上列车时间减去到达站台时间；式(4)表示乘客的平均等待时间等于车站外以及站台等待时间之和与总乘客数的比值；式(5)表示上车人数要小于列车定员与最大满载率的乘积；式(6)表示乘客的上车时间等于列车到站时间；式(7)～(9)指乘客到达、进站候车和登上列车3 种不同状态的0～1 变量；式(10)～(12)表示在站外等候、站台等候以及上车的累计乘客数量；式(13)表示站台等待人数等于上车人数及滞留站台人数之和；式(14)表示客流进站率为进站乘客数量与到站总人数之比；式(15)表示站台超限人数等于站台人数与站台容量之差；式(16)为客流控制强度约束，允许乘客进站比率越大，客流控制强度越小。

2 深度Q 网络客流协调控制

2.1 深度Q 网络

上面提出的客流控制模型属于典型的复杂约束下的非线性模型，下面使用深度Q网络进行该模型的求解，给出客流协调控制的深度Q 网络模型框架和算法流程。

如图1 所示，基于深度Q 网络的客流控制强化学习框架包括环境、状态、动作集，首先智能体将各车站的初始乘客数作为状态，输入到深度Q 网络中，网络根据Q 值更新公式，选择各车站客流控制率作为动作，将状态和动作输入到环境中进行乘客与列车之间的交互，得到下一个状态与奖励后再次输入到网络中去，以此不断迭代更新。

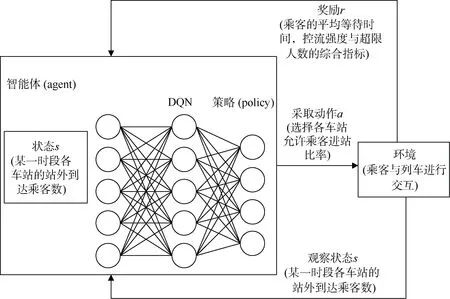
图1 基于深度Q 网络的客流控制强化学习框架 Figure 1 Reinforcement learning framework for passenger flow control based on deep q-network

2.2 客流环境

该环境可以仿真单条地铁线路上各个车站的客流到达直至上车离开的过程，通常包括3 个子流程：到达车站、进入车站、上车-下车[9]。如果单位时间内进站量的控制率大于0，则被限制进入站台的乘客应在站外等待，并根据下一阶段的控制率和上一阶段站外等候乘客的到达顺序进入车站。

2.3 车站状态

车站状态是指在单条线路某个时间步长上每个车站的进站客流需求量。每个车站的进站率随控制时间步长发生改变，而车站状态随进站率不同发生改变。

将总仿真时间分为M 个控制时间步长，控制站的进站率将会每15 min 改变一次。在控制乘客进站量的情况下，将控制时间步长m(0＜m≤M)内车站n 的状态Sm,n定义为

式中，Dm,n为在控制时间步长m 内车站n 的到站人数，为第m-1 时段车站n 的进站人数。

控制乘客进站量时，一些在步长m-1 内到达车站的乘客可能需要在车站外等候，直到下一个步长m 才允许进入车站，所以表示步长m-1 内在站外等候的乘客数量。

2.4 动作集

动作ai指的是在每个控制时间步长m 内车站n 所选择的动作，表示在步长m 内车站n 允许乘客进站数量的百分比，即控制下的进站率，则动作集A 包含了单条线路上某车站的进站量控制率。假设在控制时间步长m 内有100 人希望进入车站n，A={0.2，0.4，0.6，0.8，1.0}，对车站n 执行动作a1=0.2，则在步长m 内允许进站的乘客数量为20 人，动作a5=1.0 表示允许所有乘客进入车站。

2.5 奖励函数

奖励函数定义了强化学习问题的目标[10]。在本研究中，目标是在客流控制强度较小的情况下，尽量减少乘客在站台等待的超限数及乘客的平均等待时间。因此，奖励函数为

2.6 算法过程

强化学习算法过程如下：

?

6 遍历线路上的车站 7 根据当前状态选择动作，将动作与环境交互 8 根据环境函数得出下一状态，奖励值及站台超限人数 9 记录当前状态，动作，下一状态，奖励 10 将记录的参数传入网络进行训练 11 更新状态并打印动作及站台超限人数 12 end for 13 每一时间步长的奖励求和并更新时间步长m 14 如果m 达到需要控制的时间步长，循环结束15 end while 16 计算客流控制时段内一条线路所有乘客平均等待时间17 END

3 轨道交通客流控制实例

3.1 仿真场景

这里用一个真实线路的仿真实例来评估强化学习方法在地铁的客流协调控制中的可用性。选取北京地铁八通线在2019 年某工作日8:00—9:30 时间段进行实验，该线路的车站情况如图2 所示。

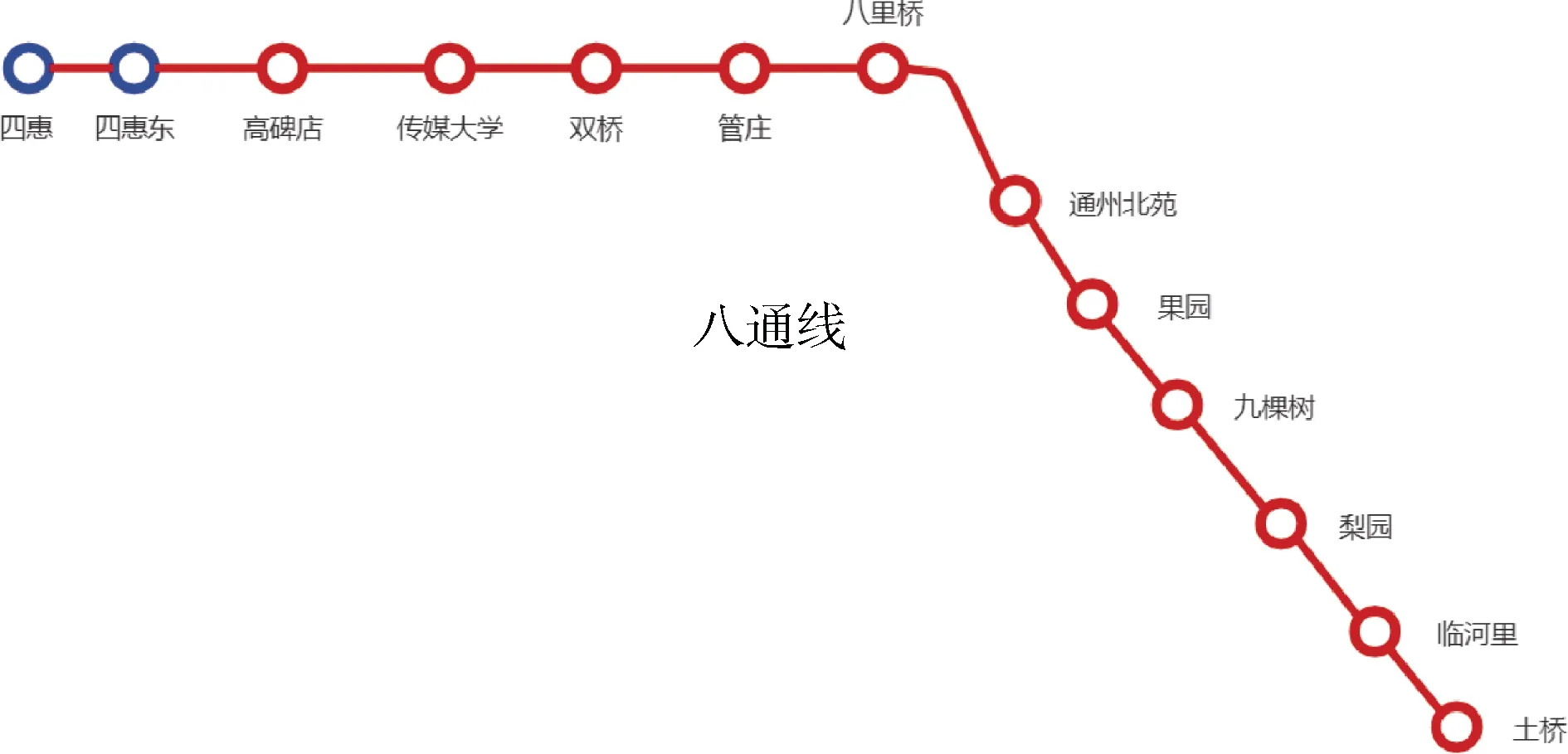
图2 北京地铁八通线线路图 Figure 2 Route map of Metro Batong Line

使用当日八通线的实际工作日运营时间表，获取当日AFC 数据OD 客流量作为实验输入，各车站分时进站量如图3 所示。该模拟在TensorFlow2.0 中调用keras 库实现，所用参数如表2 所示。共做了100 次训练，并与未采用本客流控制模型的目标参数进行比较。

3.2 结果分析

训练曲线如图4 所示。实施客流控制策略的奖励值越高，在该线路上客流控制强度较低，乘客平均等待时间和车站乘客超限人数的综合指标将会减小。由训练结果和训练曲线可知，在第38 次训练时候，奖励值达到最大，即：车站站台乘客超限量与该线路上乘客平均等待时间的综合指标最小。

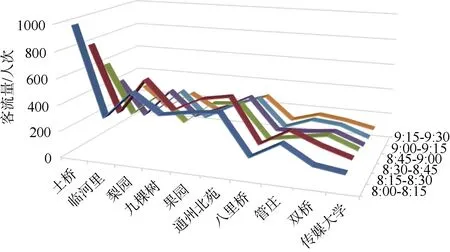
图3 不同时段的进站客流量 Figure 3 Inbound passenger flow in different periods

表2 实验参数设定 Table 2 Experimental parameter setting

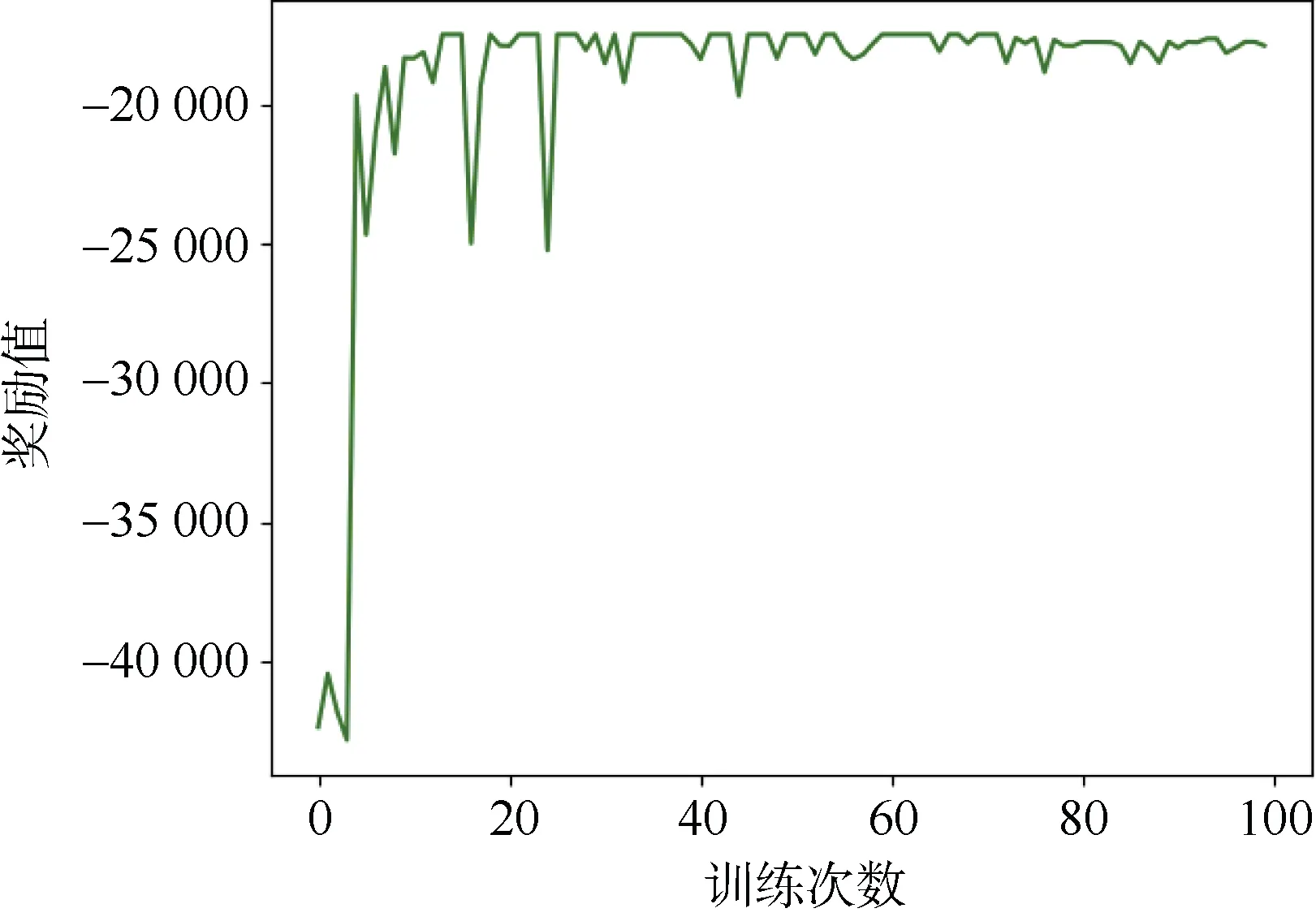
图4 训练曲线 Figure 4 Training curve

如表3 所示，与未采取客流控制相比较，采取客流控制后超限人数明显减少。同时，如表4 所示，采取客流控制的情况下，乘客平均等待时间从4 min 43 s缩短到4 min 20 s。对应的客流进站率如表5 所示。

3.3 应用讨论

本研究提出的模型，使用实际的线路、车站与列车运行计划以及实际刷卡的客流数量进行验证。在实验环境下，于15 min 之内完成了100 次迭代，并在10 min

内可以达到收敛，并开始趋于稳定。在时间效率和数据规模与特征上，均可以对实际应用实施提供支撑。

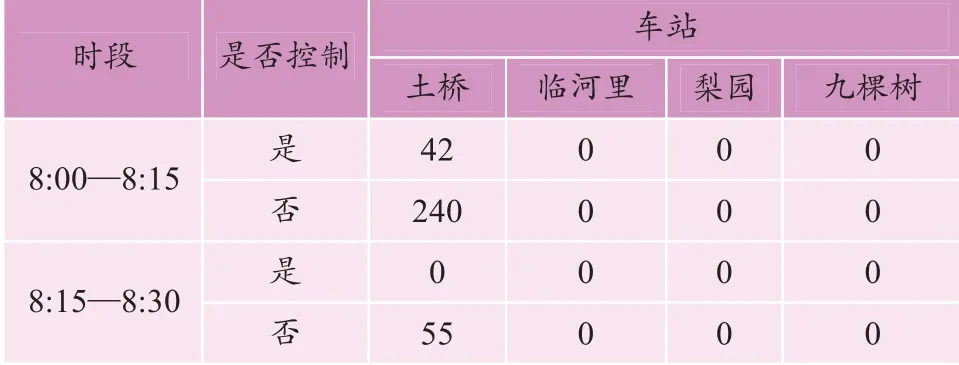
表3 各时段乘客站台超限量 Table 3 Platform overrun in each period 人

表4 平均等待时间 Table 4 Average waiting time

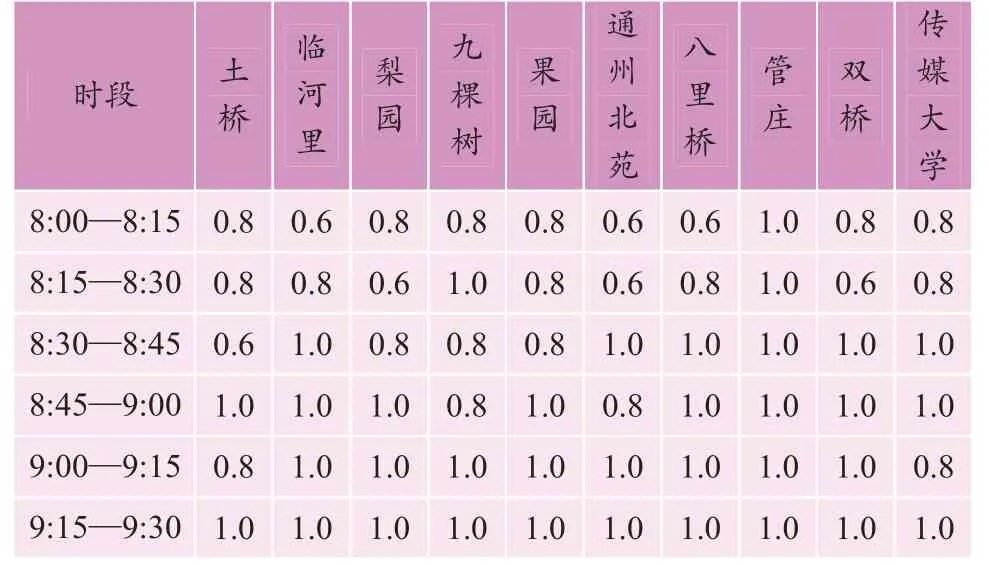
表5 地铁八通线控制车站的客流进站率 Table 5 passenger flow control strategy of Metro Batong Line

同时，本研究提出的模型在应用实施时，也需要满足一定的条件，并且还有待于进一步细化和完善，列举如下：

1) 在应用实施时，本研究提出的模型需要获取基本的数据输入，包括线路车站节点序列、列车运行计划、高峰期乘客出行OD 需求，各个车站的进站走行时间和站台的安全容量，并设置控流下的列车最大满载率。

2) 在模型应用实施时，可根据现场的要求和条件，进一步加强模型约束，并转换控制方案的表达形式。例如，根据应用要求，缩小客流控制的车站和时间范围，将进站率转化成单位时间的进站人数，以利用实施。

3) 本模型适用于线路单向大客流的控制，更适用于潮汐明显的郊区向市中心连接的线路，如果应用于线路双向大客流的控制，还需要对模型进行改进。

4 结语

本研究提出了一种基于深度Q 网络的多站客流协调控制模型，目标是在满足站台容量约束条件下，最小化地铁车站乘客的站台超限量、平均等待时间，提高客流控制强度的综合效益。使用北京地铁八通线，验证了该模型和方法的可用性。与未采取客流控制的结果相比，采取客流控制策略，可以有效降低乘客等待时间，减少车站站台乘客的超限人数，提高乘客出行效率。