零阻变换器系统中开关单元的优化分布方法

2022-06-28杨晓峰陈茂鲁郑琼林顾靖达

都市快轨交通 2022年3期

夏雪，杨晓峰，陈茂鲁，郑琼林，顾靖达

（北京交通大学电气工程学院，北京 100044）

1 研究背景

城市轨道交通输送客流量大、方便快捷，近年来获得了迅猛发展[1-2]。目前城市轨道交通多采用直流牵引供电系统，出于经济性考虑，走行轨通常兼作列车电流回流路径[3-4]。然而，走行轨存在纵向电阻，列车电流流经走行轨产生与地之间的压降，即钢轨电位[5-6]；部分电流从走行轨进入大地，形成杂散电流[7-8]。过高的钢轨电位会威胁人员安全，造成地铁停运等事故[9]；而杂散电流则会逐渐腐蚀轨道、沿线埋地金属管线等，影响其使用寿命[10-11]，因此需要采取措施加以抑制。

为限制钢轨电位，在线路中设置钢轨电位保护装置(over-voltage protection device，OVPD)，钢轨电位过高时，OVPD 动作将钢轨直接接地，但会导致更多的电流泄漏[12]。治理杂散电流的方法大致分为排流法与源头控制法[13]：前者通过加装排流网、排流柜等设备收集杂散电流[14-15]；后者则从杂散电流产生源头出发，通过提高供电电压、增加沿线牵引所数量、增大轨道对地电阻[16]、采用专用轨(第四轨)回流[17]等方法，减少杂散电流。

上述措施仅适用于新建线路，且治理效果随时间逐渐下降。近年来，基于电力电子技术的硬件治理措施受到关注，即在现有供电系统结构的基础上加装电力电子设备，相对于传统治理措施治理效果好、便于维护。Fotouhi 等采用了一种吸流(Booster)电路，使走行轨回流电流经专用回流线缆转移至牵引所负极[18]。有研究者采用基于直流自耦变压器(DC-auto transformer，DCAT)的牵引供电系统，通过DCAT 装置将走行轨电流转移至负馈线[19-20]。这两种措施均能从源头上治理杂散电流，但所采用的电力电子器件数目较多，且控制策略复杂。Gu 等提出了一种零阻变换器系统(zero-resistance converter system，ZRCS)，在传统牵引供电系统的基础上，加装开关单元、负阻变换器、回流线缆，将走行轨电流转移至增设的回流线缆[21]。Yang 等分析了ZRCS 不同部件的典型故障，验证发现ZRCS 在大多故障情形下均能降低钢轨电位[22]。该系统器件数目较少，控制简单，不影响牵引供电系统的可靠性，便于现场安装与维护。

ZRCS 的开关单元在列车运行时切换导通时序，使走行轨电流经导通的开关单元转移至牵引所负极，且非列车所在区段的走行轨电流为零；牵引所负极和导通开关单元与走行轨连接处等电位，即为虚拟回流地。作为构造零阻回路的关键部件之一，开关单元的数量与分布直接影响ZRCS 中虚拟回流地的位置与走行轨回流路径长度，也改变了钢轨电位与杂散电流的分布。

然而，现有研究多假设开关单元均匀分布情况下对ZRCS 进行分析，但在实际列车牵引曲线下，较高的钢轨电位与较大的杂散电流集中分布在列车电流较大的牵引以及制动工况下，改变虚拟回流地的分布，以缩短列车位于此两个工况内的走行轨回流路径，能够降低对应区段的钢轨电位，提高ZRCS 的综合治理效果。

因此，笔者提出开关单元的优化分布方法。首先介绍开关单元在构造虚拟回流地与零阻回路时的作用，随后分析开关单元数量、分布优化的必要性与优化方法，最后根据典型列车运行线路对所提出的优化分布方法进行仿真验证。

2 ZRCS 工作原理

如图1 所示，ZRCS 在传统牵引供电系统(conventional traction power system，CON-TPS)的基础上，在牵引所(traction substation，TS)负极处设置两个负阻变换器(negative resistance converter，NRC)，n 个开关单元(switch unit，SU)沿线分布，经回流线缆(returning cable，RCA)连接，把走行轨划分为(n+1)个区段。

图1 ZRCS 结构 Figure 1 Illustration of ZRCS

在本研究中，负阻变换器、开关单元的典型拓扑分别如图2(a)、(b)所示。SU 为双向导通开关，随列车的移动，对应的SU 切换通断状态，使得仅列车所在区段两侧的SU 导通。NRC 为双极性输出的电力电子拓扑，根据导通的SU 及RCA 生成参考电压，通过控制各IGBT 的通断输出双极性电压，实时构造零阻回路，将走行轨电流转移至牵引所负极。

如图3 所示，以列车位于区段k 为例(1≤k≤(n+1)，k 为正整数)，SU-(k-1)与SU-k 导通，NRC1 抵消RCA-1～RCA-(k-1)与SU-(k-1)的压降，NRC2 抵消

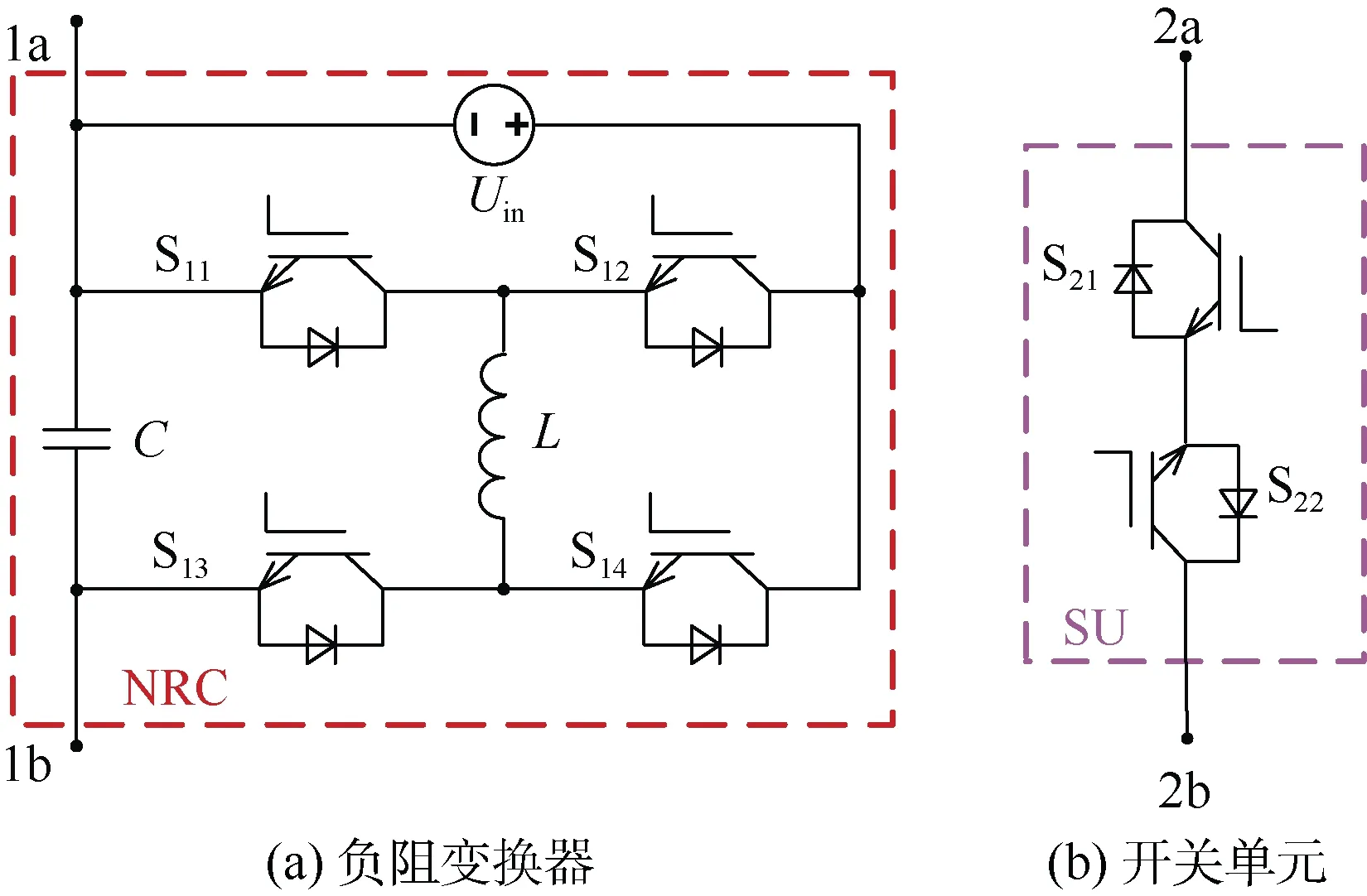
图2 关键部件拓扑 Figure 2 Topology of Key Components

图3 列车位于区段k 时ZRCS 的工作原理 Figure 3 Operation principle of ZRCS when the train is in rail-section k

RCA-(k+1)～RCA-(n+1)与SU-k 的压降(见式(1))；NRC1、NRC2 的等效电阻与对应的RCA 及SU 的电阻之和为零，等效为两条零阻回路(见式(2))。具体计算如下：

式中：uzr为零阻回路的等效电压，uNRC为NRC 的输出电压，uSUon为SU 的导通电压，uRCA为RCA 的电压；Rzr、RSUon、RNRC分别为零阻回路、SU、NRC 的等效电阻，RRCA为RCA 的电阻。

同时，走行轨上与导通的SU 相连接处构造虚拟回流地(returning euqi-point，REP)，将回流路径由整个走行轨缩短至区段k，以此减少走行轨电流泄漏，从而降低钢轨电位。

在零阻变换器系统中，各SU 的工作模式根据列车位置检测[23]的结果确定；NRC 实时采集导通SU 及连接两者的RCA 的压降生成参考电压，以实现零阻回路的构造。

3 开关单元优化分布

零阻变换器系统能随列车运行移动虚拟回流地的位置，将部分区段的走行轨电流转移至回流线缆，实现钢轨电位与杂散电流的降低。而开关单元作为可能的虚拟回流地的位置，其分布将会影响钢轨电位的分布。

为得到较优的开关单元分布方案，需确定SU 的数量n。当SU 均匀分布时，随着其数量的增加，回流地间的距离逐渐缩短。如图4 所示，n 增加，虚拟回流地AREP位置移动，回流路径长度l 减小，钢轨电位也相应降低。理论上n 越大、l 越小，则对钢轨电位的治理效果越好，但ZRCS 整体建设成本也会不断增加。

图4 不同SU 数量下ZRCS 的钢轨电位 Figure 4 Rail potential of the ZRCS under different quantities of SUs

在实际运行过程中，当列车处于牵引或制动工况时，相应的列车电流远大于匀速工况，导致其钢轨电位与杂散电流较大。调整此部分回流地间的距离，能降低钢轨电位，减少杂散电流，进而提高ZRCS 的综合治理效果。

因此，本研究对ZRCS 的开关单元数量及分布进行优化。考虑到列车运行中大部分时间处于匀速工况，所以在进行SU 数量优化时，以列车牵引电流恒定为条件，分析n 个SU 均匀分布时的钢轨电位、杂散电流分布，以确定较优的SU 数量。

以单车情形为例的SU 优化分布策略如图5 所示。对SU-k 进行位置优化时，列车应在此SU 两侧的区段k 与区段(k+1)运行，此时SU-k 处于工作状态，其位置能直接影响REP 的位置与ZRCS 的钢轨电位分布，对SU 位置分布的优化才有意义。

图5 SU 优化分布策略 Figure 5 Optimal distribution strategy of the SU

无论是单车还是多车情形，开关单元位置优化的基本方法都相同，均通过调整SU 的分布，移动虚拟回流地REP 的位置，以改变回流路径的长度，从而获得更优的治理效果。

为简化分析，本研究定义平均杂散电流与作用时间的乘积，即总泄露电量Qsum，计算如下：

式中，is为杂散电流，Isav为杂散电流平均值，T 为杂散电流作用时间(即列车运行时间)。

由式(3)可知，总泄露电量的大小取决于杂散电流的大小以及杂散电流在金属结构上作用时间T 的长短。

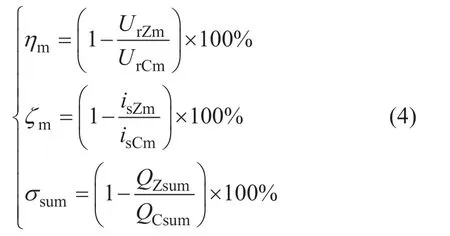
为了评估列车运行过程中ZRCS 的治理效果，定义最高钢轨电位、最大杂散电流与总泄漏电量的降低百分比ηm、ζm与σsum，有式中，UrZm、isZm、QZsum分别为ZRCS 的最高钢轨电位、最大杂散电流、总泄露电量，UrCm、isCm、QCsum分别为CON-TPS 的最高钢轨电位、最大杂散电流、总泄漏电量。

4 开关单元仿真验证

4.1 数量优化

为简化分析，作如下假设：一是牵引所等效为恒压源，忽略内阻及各牵引所输出电压的差异；二是忽略电流跨区间传输对钢轨电位的影响。搭建图1 所示的仿真模型，依据表1 仿真参数得到ZRCS 的最高钢轨电位、最大杂散电流、总泄漏电量降低百分比随SU数量n 变化的曲线。

表1 系统参数 Table 1 System parameters

如图6 所示，开关单元均分时，随着n 增加，ZRCS的最高钢轨电位、最大杂散电流、总泄漏电量的降低百分比呈现逐渐上升的趋势，但最大杂散电流的降低百分比在n=3 时略有下降。这是因为回流路径中点处杂散电流较大，且列车位于SU 处时，理论上该处SU导通即可，但ZRCS 中的SU 导通策略致使该区段两侧的SU 均导通，造成区间中点处的杂散电流升高，即最大杂散电流降低百分比的下降。

图6 降低百分比 Figure 6 Mitigation percentage

当SU 数量n＞4 以后，降低效果曲线已逐渐平缓，即使增大n，降低百分比也仅能提高5%甚至更小，不能充分利用SU，反而增加了建设成本；当n＜2 时，降低效果不够理想。因此n 取2～4 时，能够兼顾建设成本以及治理效果，综合考虑后选取n=3 对ZRCS 进一步分析。

4.2 优化分布

在实际列车运行线路中，通常在两个牵引所之间有一个降压所车站，列车需在此车站停站。本研究在仿真时，选取北京地铁亦庄线“荣昌东街—同济南路—经海路”路段进行分析。为简化分析，设置相邻两车站之间的距离为2.5 km，即区间长度为5 km，同济南路站为降压所车站，停站时间取为30 s[14]，牵引曲线如图7 所示，列车在两个牵引所之间完成两次“牵引-匀速-制动”的过程，且总运行时间T=315 s。

图7 列车牵引曲线 Figure 7 Traction curve of the train

根据SU 数量优化的结果，设置3 个SU 分布在TS1～TS2 之间，将走行轨划分为4 个区段。为兼顾整条线路的治理效果，将SU-2 设置在2.5 km 处，SU-1与SU-3 分别设置在区间中点(即降压所处)两侧。

4.2.1 SU-1 位置优化

结合图7 牵引曲线，分析列车运行于区段1(TS1～SU-1)、区段2(SU-1～SU-2)，SU-1 位置变化时走行轨全段的最高钢轨电位、最大杂散电流及总泄漏电量降低百分比的变化趋势。

如图8 所示，SU-1 设置于区间中点左侧2.1～2.4 km时，列车在此段处于电流较大的制动工况内，整体的降低效果优于其他位置。SU-1 设置在A、B、C 三点处分别取得了最高钢轨电位、最大杂散电流以及总泄漏电量的降低百分比最大值，分别是79%、86%、74%。在AB 段内最高钢轨电位取得最大治理效果，曲线较为平缓，而最大杂散电流以及总泄漏电量的降低百分比曲线斜率较大；在BC 段内，ηm、ζm的变化趋势均已十分缓慢，但随着SU-1 位置的改动，总泄漏电量的降低百分比曲线增长至最大值，因此认为当SU-1 位于C 点，即走行轨上2.2 km 处，能够获得较好的治理效果。

图8 降低百分比 Figure 8 Mitigation percentage

4.2.2 SU-3 位置优化

分析列车运行于区段 3(SU-2 ～SU-3)、区段4(SU-3～TS2)，SU-3 位置变化时走行轨全段的最高钢轨电位、最大杂散电流以及总泄漏电量降低百分比的分布趋势。

在图9 所示的降低百分比曲线中，SU-3 设置于区间中点右侧2.6～3 km 时，列车在此段内处于电流较大的牵引工况，ZRCS 的整体降低效果优于其他位置。SU-3 设置于D 点处的最高钢轨电位、总泄漏电量的降低百分比分别取得了最大值91%与74%，在E 点处的最大杂散电流取得最大降低百分比，为82%。在DE 段内，最高钢轨电位降低百分比曲线以较大的斜率衰减，而最大杂散电流以及总泄漏电量降低百分比曲线斜率较小，因此认为当SU-3 位于D 点(即走行轨上2.8 km 处)时，能够获得较好的治理效果。

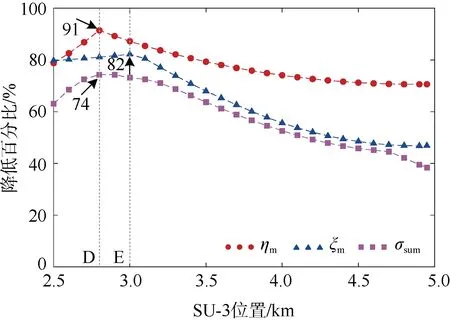
图9 降低百分比 Figure 9 Mitigation percentage

在实际列车运行中，各线路长度不同、列车牵引曲线也不完全相同，无法做到对每一条线路进行具体的SU 分析。考虑到列车的牵引曲线基本走势一致，对类似于本研究所分析的“荣昌东街—同济南路—经海路”路段的线路，将SU 设置在列车电流较大的降压所附近的位置，即牵引曲线中第一个制动工况以及第二个牵引工况内，均能够获得较为理想的降低效果。

4.3 优化后的ZRCS

根据上述优化结果，针对所分析的情形，设置3 个SU 分布于走行轨上2.2、2.5 和2.8 km 处，对SU 优化后ZRCS 的钢轨电位、杂散电流及总泄漏电量分布进行分析，并与CON-TPS、SU 均分时的ZRCS 进行对比。

CON-TPS 与SU 优化后ZRCS 的钢轨电位三维分布如图10 所示。在CON-TPS 中，回流路径的长度始终为L，牵引以及制动工况下的钢轨电位相比于匀速工况要高，且基本分布与列车牵引曲线的变化趋势相似。对于SU 优化后的ZRCS，回流路径的长度随着虚拟回流地位置的改变缩短为11L/25、3L/100、3L/100 和11L/25，因此钢轨电位也整体小于CON-TPS。

图10 钢轨电位三维分布 Figure 10 Three-dimensional distribution of rail potential

由图11 及表2 可知，相比于CON-TPS，SU 优化后，列车处于第一个制动工况(109.7～142.3 s)时，钢轨电位的绝对值峰值降低为3.4 V，降低了约88.9%，杂散电流峰值降低为0.2 A，降低了约92%；列车处于第二个牵引工况(172.3～207.8 s)时，钢轨电位、杂散电流峰值分别降低为2.61 V 与0.2 A，分别降低了约88.8%和89.5%；总泄漏电量降低为29.78 C，降低百分比提高至74.7%。

图11 SU 优化前后的钢轨电位及杂散电流分布 Figure 11 Rail potential and stray current before and after SU optimization

表2 总泄漏电量 Table 2 Total leakage charge

结合图11，在CON-TPS 与SU 优化前的ZRCS中，区间中点附近为全线钢轨电位及杂散电流较高的区段，1、3 区段的钢轨电位、杂散电流峰值分别达到了1、4 区段的2～5 倍。优化后，SU 集中分布在区间中点附近，中点两侧制动与牵引工况下的回流路径缩短，钢轨电位及杂散电流的降低百分比均提高，如图12 所示。但在SU 数量一定时，走行轨上各段回流路径的长度互相关联，因此对于2、3 区段内较高的钢轨电位的显著降低需要牺牲1、4 区段内的较低的钢轨电位的治理效果。