考虑列车运行工况的钢轨电位硬件动态模拟平台

王双慧，杨晓峰，王慧康，郑琼林

（北京交通大学电气工程学院，北京 100044）

1 研究背景

城市轨道交通具有运力大、速度快、节能环保、不受气候影响等优点，近年来获得快速发展。截至2020 年，我国城市轨道交通运营线路总里程达7 978 km[1]。城市轨道交通广泛采用直流牵引供电系统，牵引所通过接触网(或第三轨)向列车供电，并通过走行轨回流[2]。数千安培的列车电流流经每千米数十毫欧的走行轨会产生钢轨电位问题，过高的钢轨电位会危及人员及设备安全[3]。走行轨与大地之间并非完全绝缘，部分电流会泄漏至周边介质或大地中，形成杂散电流[4-5]。杂散电流容易导致钢筋混凝土结构及其他埋地金属结构的腐蚀，极端情况下会严重损坏其结构，减少使用寿命[6-8]。

常见的钢轨电位与杂散电流治理措施包括：降低走行轨电阻、增强走行轨-大地间绝缘、提高供电系统电压等级、缩短牵引所间距、采用杂散电流收集网等[9-13]。但受环境因素的影响，上述措施随着时间推移逐渐恶化，依然存在杂散电流泄漏现象[14]。一些研究者提出利用电力电子技术实现对杂散电流的治理[15-18]，为杂散电流的治理提供了新思路。然而，上述治理措施直接用在现场，开展实验的协调难度大。钢轨电位硬件动态模拟平台(rail potential hardware dynamic emulator，RPHDE)，能突破时空约束，再现钢轨电位的动态分布规律，为硬件治理措施的采用提供物理验证平台。王慧康等提出了一种电力电子的硬件动模方法[19]，但其可变电阻模块仅能模拟列车单一运行工况下的钢轨电位。为此，杨晓峰等研究了一种改进的可变电阻模块[2]，以适应不同列车运行工况，但拓扑相对复杂。而徐杰等提出了一种简化拓扑[11]，采用固定电阻模拟走行轨-大地的过渡电阻，但未考虑列车运行工况影响。

为此，本研究提出考虑列车运行工况的钢轨电位硬件动态模拟平台(简称“硬件动模平台”)。首先，分析直流牵引供电系统模型和钢轨电位模型，将分布参数的回流系统简化为集中参数电阻网络，提出低阻模块(low resistance module，LRM)模拟接触网与走行轨纵向动态电阻、高阻模块(high resistance module，HRM)模拟走行轨-大地动态过渡电阻的方法；然后，在分析LRM 与HRM 工作原理的基础上，提出考虑列车运行工况的硬件动态模拟平台及其控制策略；最后，通过仿真和实验，对上述理论和控制进行验证。

2 牵引供电系统建模

直流牵引供电系统基本结构如图1 所示，由牵引所、上/下行接触网(或第三轨)、回流系统、列车构成。为方便分析，假定直流牵引供电系统中全线路上/下行轨道、接触网分别贯通。当列车牵引出站时，沿线路所有牵引所为列车提供电流，各牵引所与列车构成供电回路。

图1 直流牵引供电系统基本组成 Figure 1 Configuration of a DC traction power supply system

2.1 列车与牵引所模型

作为直流牵引供电系统的主要负载，列车通常被等效为一个电流源[20]，牵引电流随列车运行工况变化。

牵引所TPS 的整流机组采用24 脉波不控整流。整流机组外特性与交流侧电感、移相变压器的漏感、变压器耦合系数以及整流器接线方式等多种因素有关，外特性为多段曲线[21]。为简化分析，本研究将整流机组等效为电压源串联内阻的形式。

2.2 供电回流系统建模

回流系统为无数微元段构成的电阻网络，具有分布参数特征。仅考虑走行轨-大地两层模型的数学模型如图2 所示，其中Rr表示单位长度走行轨纵向电阻(Ω/km)，Rg表示单位长度走行轨-大地过渡电阻(Ω·km)。供电区间的起点坐标为L(km)，终点坐标为L+ΔL(km)，区间长度为ΔL，流入起点处的电流为Ir1，流出终点的电流为Ir2。在微元段dx 中，ir(x)表示x 处轨道电流，urg(x)表示x 处钢轨电位。

图2 回流系统两层分布模型与微元段 Figure 2 Two-layer distribution model and micro-element segment model of a recirculation system

根据图2 微元段，得到任意位置x 处钢轨电位Urg(x)与轨道电流Ir(x)表达式

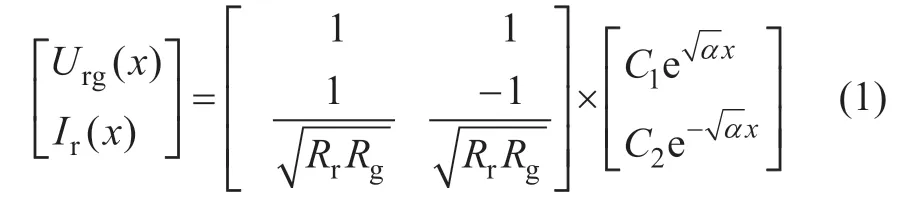
式中，α=Rr/Rg为波阻抗传播系数。

由式(1)可知，当供电回路内电阻参数及区间长度确定时，钢轨电位与轨道电流表达式中的系数C1、C2由边界条件确定。

设单列车单牵引所的区间长度为Ls，边界处的钢轨电位为Ur1、Ur2，区间内的边界条件为

由式(1)解得，待定系数C1、C2为

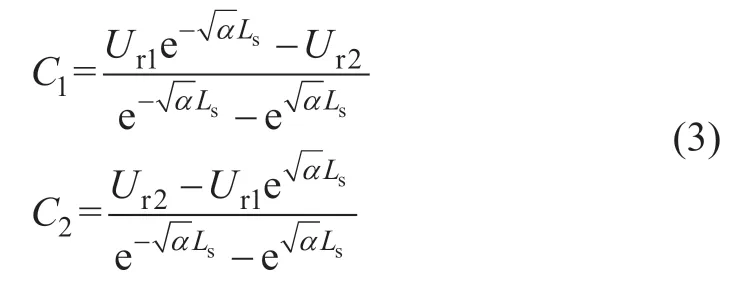
3 钢轨电位理论计算

基于列车与牵引所的等效电路，笔者以两列车3个牵引所为例，建立了图3 所示的直流牵引供电系统模型。以列车和牵引所位置作为截面，将线路划分为4 个区段。其中，牵引所空载电压和支路电流分别为Udi、Idi，牵引所内阻Rini，列车电流为Iti。截面i 处走行轨电位为Uri，接触网电压为Uci，截面i 与i+1 之间走行轨电阻为Rri，接触网电阻为Rci。

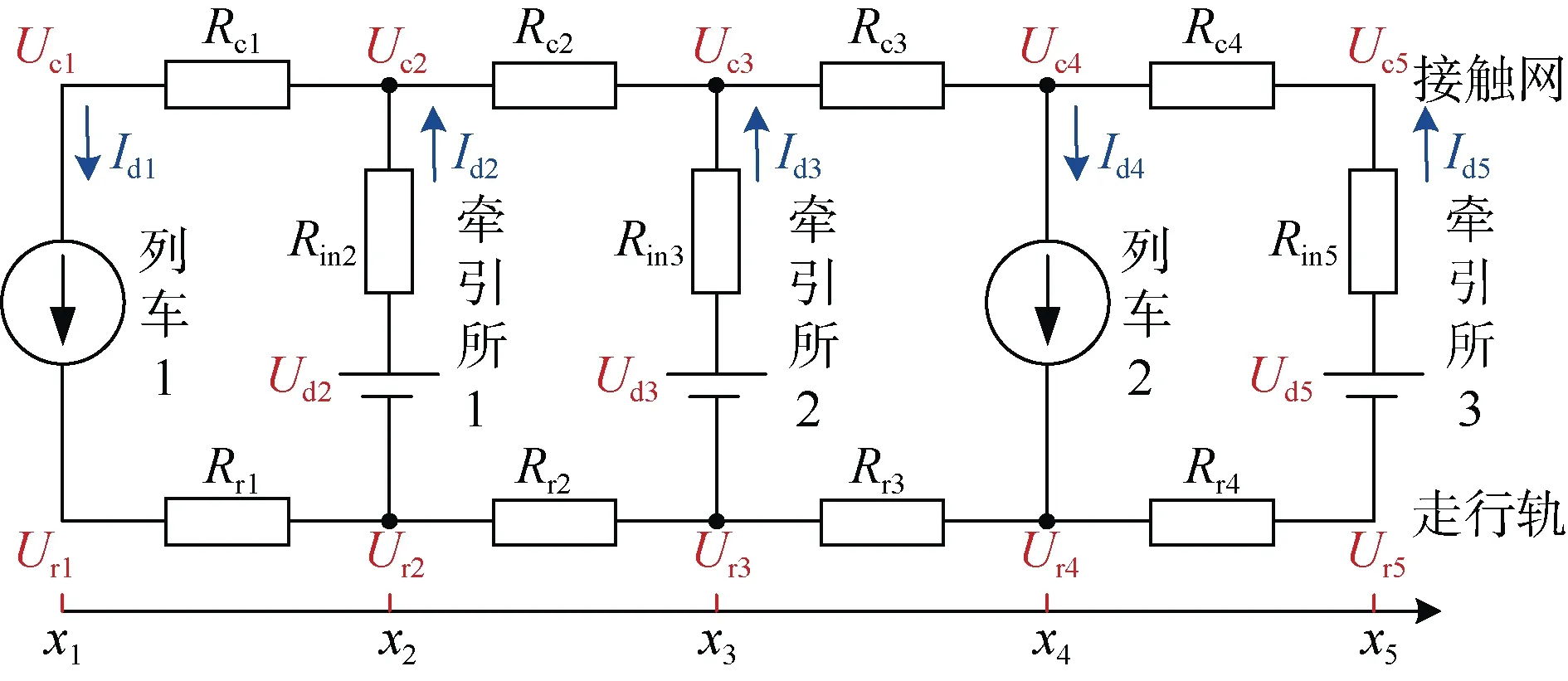
图3 直流牵引供电系统模型 Figure 3 DC traction power supply system model

在截面x1～x5中，建立截面导纳子矩阵Yi。截面i 与截面i+1 之间的阻抗子矩阵可建立为Zi，Yi与Zi-1共同构成导纳矩阵。在截面xi处，节点电压矩阵与注入截面电流矩阵定义为Ui与Ii。对上述模型列写节点电压方程，得到

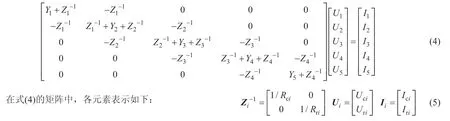
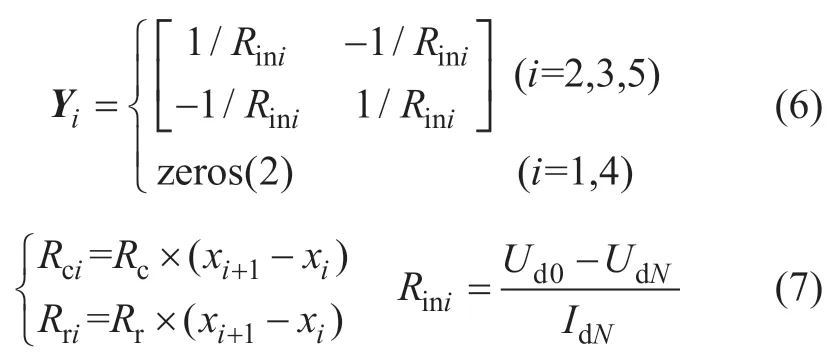
当线路参数与列车牵引特性确定时，流入截面的电流[I1；I2；I3；I4；I5]、导纳矩阵Yi与Zi-1均为已知。由式(4)即可求得系统分析模型中的各点电位，由此求得牵引所的支路电流Idi如下：

考虑列车之间不同工况下的电流耦合，牵引所电流与列车电流满足

式中，λ1～λ5定义为分流系数。

当列车工况不同时，其分流系数如表1 所示。

表1 分流系数与列车工况关系 Table 1 Relationship between λ and train operating condition

列车1 和列车2 的功率分别为P1、P2。当两列车同为牵引工况时，λ3、λ4、λ5=0，P1＞P2，λ1=1；P1＜P2，λ2=1。当列车1 牵引、列车2 制动时，P1＞P2，λ1～λ4=1；P1＜P2，λ1、λ2、λ4=0。当列车2 牵引、列车1 制动时，P1＞P2，λ1、λ2、λ4=1；P1＜P2，λ1、λ2、λ4=0。由上述分析可知：

1) 两列车在不同工况下，线路存在多个供电回路；

2) 列车不同工况与功率，会影响系统潮流分布；

3) 当列车不同工况时，列车电流存在跨区间传输，其传输距离跨越多个供电区间。

图4 列车1 与牵引所2 之间的供电回路 Figure 4 Power supply circuit between train1 and TPS2

接下来以表1 的工况3 为例，分析回路电流对钢轨电位的影响。线路中存在4 个供电回路，各供电回路电流与钢轨电位微元模型如图4 所示。供电回路 电流Id2将线路划分为供电区间1 和回流区间2，其中：供电区间1 的钢轨电位为Ur1(x)，轨道电流为Ir1(x)；回流区间2 的钢轨电位为Ur2(x)，轨道电流为Ir2(x)。 沿线路分布的钢轨电位与轨道电流公式如下：

其边界条件为

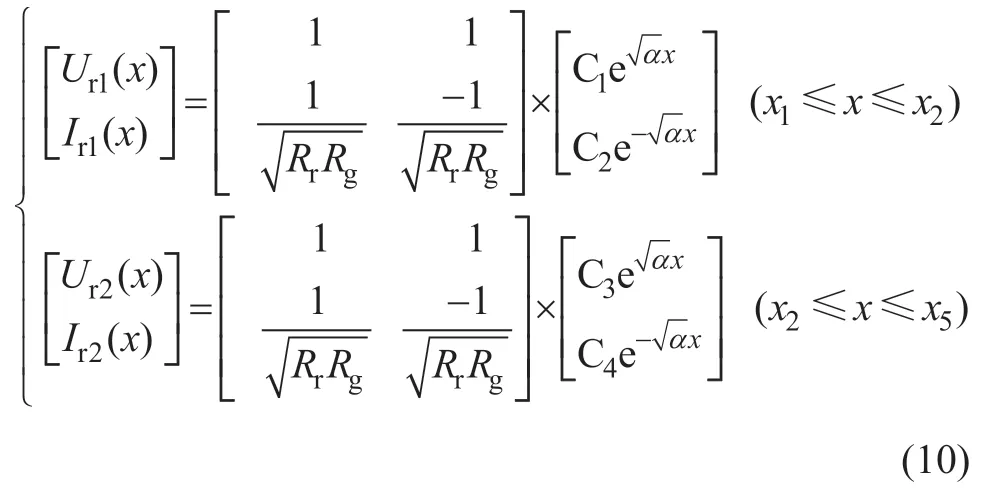
通过上述边界条件，得出回路电流Id2对全线路钢轨电位与轨道电流的表达式。以此类推，可以求解出回路电流Id3、It4、Id5对全线路的钢轨电位与轨道电流，最后进行叠加，得到沿线钢轨电位的分布情况。

在牵引所或列车数量发生变化时，采用同样的方法建立节点电压方程，并改变导纳矩阵，求得支路节点电位与支路电流。首先根据列车工况及电流确定系统中存在的回路电流，其次计算不同供电回路电流对全线路钢轨电位与轨道电流的影响，最后进行叠加得到全线路钢轨电位。

由上述分析可知，在直流牵引供电系统中，电流的回流路径受到列车运行工况与瞬时功率的影响。

4 可变电阻模块模拟

前述回流系统建模均基于分布参数的电阻网络，无法直接用于硬件动模实现，为此有必要将分布参数的电阻网络转换为集中参数模型。本研究采用集中参数电阻等效模拟ΔL 段内的微元电阻，并采用可变电阻模块模拟其外特性。

4.1 集中参数模型特性

如图5 所示，π 型集中参数模型中走行轨电阻为Zr，走行轨对地过渡电阻为Ryg1、Ryg2，流入起点电流为Ir1，流出电流为Ir2，起点处钢轨电位为Ur1，终点处钢轨电位为Ur2，流过Zr的电阻为Ix。

图5 回流系统集中参数等效 Figure 5 Lumped parameter equivalence of the returned system

根据图5 的集中参数模型，区间L～(L+ΔL)内回流系统的等值参数满足下述关系，即

整理式(12)，可得到集中参数模型中钢轨电位与轨道电流的关系如下：

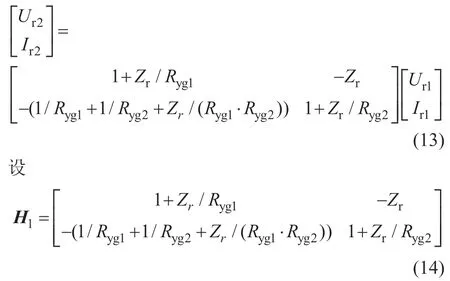
式中，H1表示由起点处电流与钢轨电位到终点处电流与钢轨电位的转换矩阵。

在分布参数模型下，各起点与终点处钢轨电位与轨道电流的关系如下： 设

式中，H2表示由起点处电流与钢轨电位到终点处电流与钢轨电位的转换矩阵。

根据边界位置处轨道电流与钢轨电位的关系，令H1=H2，得到

由式(17)，得到集中参数模型下走行轨纵向电阻Zr以及走行轨-大地过渡电阻，即

由以上分析可知，长度为ΔL 的回流系统采用集中参数模型替代，替换前后的钢轨电位和电流保持不变，且集中参数模型中的阻抗仅与区间内回流系统自身参数与区间长度ΔL 有关。

4.2 可变电阻模块特性

列车两侧接触网电阻、走行轨纵向电阻与走行轨-大地过渡电阻的特性随列车位置变化，图6 为单供电区间系统模型。

图6 单供电区间系统模型 Figure 6 Single power supply interval system model

当列车在长度为L 的供电区间运行时，左右侧牵引所位置分别为0 和L，列车位置为S。由式(18)，列车左右两侧接触网电阻Rc，走行轨电阻Rr，走行轨-大地电阻Ry与列车位置S 满足如下关系，即

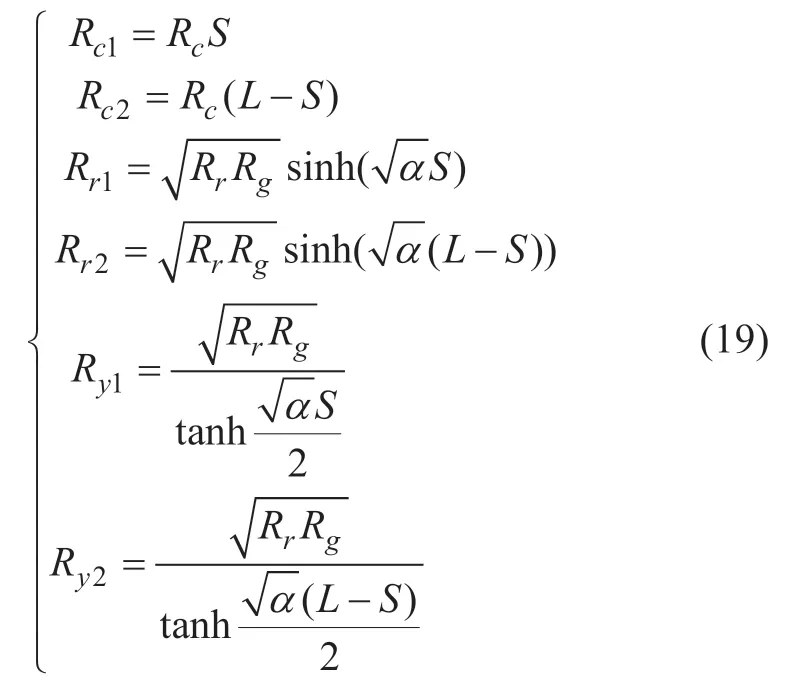
列车位置对地过渡电阻Ry为固定值，即

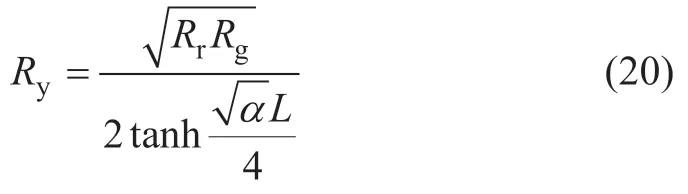
接触网电阻Rc1、Rc2的等效阻值范围为[0，RcL]，走行轨电阻与Rr1、Rr2的等效阻值变化范围为[0，RrL]，与列车位置呈线性关系。走行轨对地过渡电阻Ry1、Ry2的等效阻值变化范围为[2Rg/L，+∞)，与列车位置S 为反比关系。

4.3 LRM 拓扑工作原理

图7 所示的低阻模块LRM 用来模拟走行轨纵向动态电阻，LRM 由电阻Rol、开关管S1与S2、Rel-Cl支路以及电感Ll构成。两个开关管反向串联，使LRM能够在双向电流下工作。

图7 LRM 拓扑 Figure 7 Topology of LRM

根据电流的流动方向，LRM 具有两种典型的工作模态。在两种工作模态下，LRM 具有相同的等效电路，以端口1 流入为例分析其工作原理。

根据电感电流伏秒平衡，LRM 等效输出阻值为

可见，通过控制Dl，即可控制LRM 输出阻值，进而模拟随列车移动的接触网电阻Rc与走行轨电阻Rr。

4.4 HRM 拓扑工作原理

如图8 所示，高阻模块HRM 用来模拟随列车移动的走行轨-大地动态过渡电阻，它由输入电阻Rih、输入电容Cih、反向串联开关管S1与S2及S3与S4、输出电阻Roh、输出电容Coh以及储能电感Lh构成。通过控制开关管开通或关断，使得HRM 能够在双向输入电压下工作。 HRM 在输入电压极性不同时有两种工作模态。在输入电压Uih＞0 时，S2、S4常闭、S1、S3互补导通；在Uih＜0 时，S1、S3常闭、，S2、S4互补导通。在两种工作模态下，HRM 具有相同的等效电路，故以Uih＞0 为例分析工作原理，可分为两个典型工作阶段。

图8 HRM 拓扑 Figure 8 Topology of HRM

阶段1：开关管S1导通，S3关断，时间为DhTsh，电感Lh被充电。根据小纹波近似法，此阶段电感电流满足

阶段2：开关管S3导通，S1关断，关断时间为(1-Dh)Tsh。电感电流通过S3、S4续流。此阶段电感电流满足

根据电感电流伏秒平衡，联立式(22)、(23)，可得

由小纹波近似法，假设输入电流为恒定值，可得

由能量守恒原则，输入功率与输出功率相等，得到

联立式(24)～(26)，可得HRM 等效输出阻值为

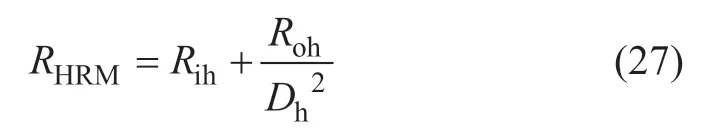
控制开关管占空比Dh即可控制HRM 阻值，进而模拟随列车移动的走行轨-大地过渡电阻Ry。

5 钢轨电位模拟平台

5.1 单供电区的钢轨电位模拟系统

列车由电流源Itr模拟，牵引所由电压源U1、U2模拟。LRM-1 与LRM-2 用于模拟接触网电阻与走行轨电阻Rc1、Rc2、Rr1与Rr2；HRM-1 与HRM-2 用于模拟走行轨对地过渡电阻Ry1、Ry2，其阻值满足式(19)。列车位置与大地间的过渡电阻为固定阻值，其数值满足式(20)。

5.2 考虑列车工况的控制策略

为实现RPHDE 在不同列车运行工况下对钢轨电位和杂散电流分配规律的模拟，本研究采用了图9 所示的控制策略。

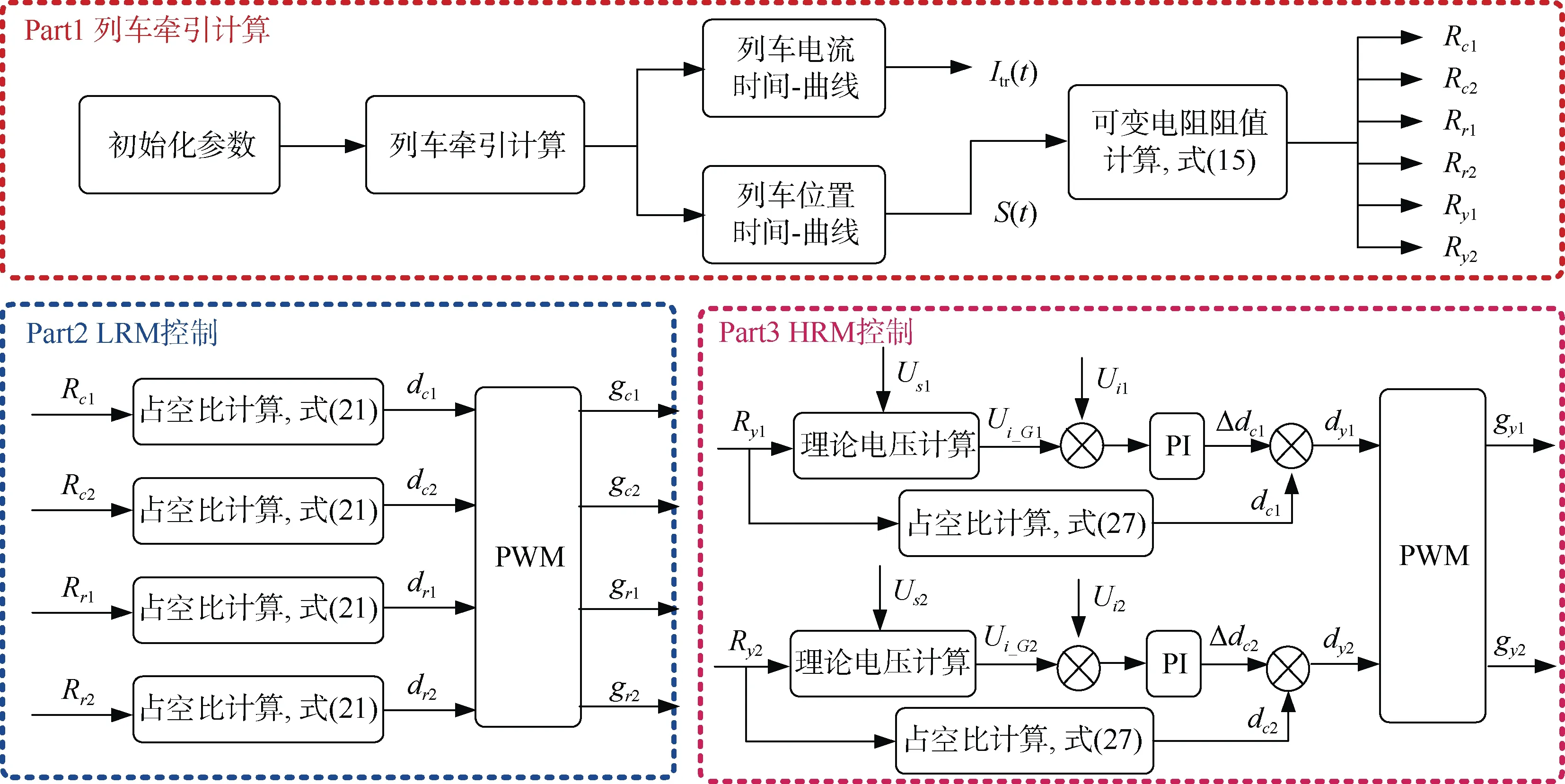
图9 考虑列车运行工况的钢轨电位模拟系统控制框图 Figure 9 RPHDE control strategy by considering operating conditions

Part 1 为列车的牵引计算及可变电阻值的计算。首先选定模拟目标线路及线路参数，如供电区间的长度、回流系统参数等。其次，根据列车的牵引计算曲线，得到列车电流随时间变化的曲线Itr(t)、列车位置随时间变化的曲线S(t)，Itr(t)用于设置电流源参数，根据S(t)及式(19)可计算出可变电阻控制的目标阻值。

Part 2 为LRM 的控制。LRM 采用开环控制，利用Part 1 计算的走行轨电阻Rr1、Rr2及接触网电阻Rc1、Rc2的目标阻值作为RLRM，通过式(21)、RLRM与占空比DL的关系，得到LRM 的控制信号gr1、gr2、gc1、gc2。

Part 3 为HRM 的控制。HRM 采用闭环控制，利用Part 1 计算的走行轨-大地过渡电阻Ry1、Ry2的目标阻值作为RHRM，通过式(27)、RHRM与占空比DH的关系，得到HRM 的控制信号gy1、gy2，结合输入电压的极性，给出对应开关管的驱动信号。

6 仿真与实验验证

结合数学模型计算结果以及模拟系统实验结果进行对比，验证所提系统拓扑、控制的正确性。由于实际列车运行过程中电流峰值可达数千安培，而单位长度的走行轨纵向电阻通常小于10 mΩ/km，在不改变钢轨电位幅值和分布规律的基础上，将列车电流和走行轨纵向电阻、走行轨-大地过渡电阻进行缩放，得到硬件动模平台参数，分别如表2～4 所示。

表2 动模系统实验参数 Table 2 Experimental parameters of a dynamic emulator

表3 LRM 仿真参数 Table 3 LRM simulation parameters

表4 HRM 仿真参数 Table 4 HRM simulation parameters

采用上述电路参数，搭建如图6 所示考虑列车运行工况的钢轨电位硬件动态模拟平台，得到牵引所1 处、列车处的钢轨电位动态分布结果，如图10 所示。

图10 考虑列车运行工况的钢轨电位实验波形 Figure 10 Experimental waveforms of the rail potential considering

由实验结果可知，牵引所处与列车处钢轨电位大小相等，方向相反，满足钢轨电位分布特征。随着列车运行工况改变，列车处钢轨电位最大值为4.8 V，由前述的钢轨电位理论计算，结合线路参数，计算出实际线路列车处的钢轨电位为4.84 V，偏差为0.7%。

7 结论

笔者研究了考虑列车运行工况的钢轨电位硬件动态模拟平台的拓扑及其控制策略，通过理论计算、仿真结果与实验验证，得到了以下结论：

1) 直流牵引供电系统中电流的回流路径受列车运行工况与瞬时功率的影响。

2) LRM 能模拟走行轨纵向电阻与接触网电阻的动态变化，HRM 能模拟走行轨-大地过渡电阻的动态变化，二者在双向电压输入时阻值可调，具有较好的稳态精度和动态特性。