新课程下高考和教材在数学文化中的呼应
2022-06-27安徽省合肥市第三中学邮编230001
安徽省合肥市第三中学 张 丽 (邮编:230001)
安徽省合肥市第三十二中学 严国华 (邮编:230051)
关键字 数学文化;高考;实例分析;教学建议
《普通高中数学课程标准(实验)》(以下简称《课标》)提倡体现数学的文化价值,近几年的《普通高等学校招生全国统一考试大纲》(以下简称《考纲》)中提出:要展现数学的科学价值和人文价值,体会数学的美学含义等要求.《考纲》与《课标》必然互为呼应. 为此笔者整理了近5 年来蕴含数学文化知识的高考真题,并挖掘它们在教材中的身影,以期对高中数学的日常教学有所启示.
1 “数学文化”的概念
从字面上理解,“数学文化”即“数学的文化”,狭义上,数学文化是指数学的思想、方法、精神以及它们的形成与发展;广泛的描述还应该包含数学史、数学美学、数学教育、数学发展中的人文部分,数学与各种文化以及社会的关系等. 它重在对人的数学教化,即让人具备用数学的语言描述世界,用数学的思维去研究、探索世界.
2 近5 年体现数学文化知识的高考题分布
笔者整理了2017-2021 共5 年的全国各省市(地区)的各种版本的高考卷中蕴含数学文化知识的42 道真题,列表如下表1.

表1

?
从高考题的分布上看,近两年高考卷几乎每一版都设置了数学文化试题,
3 教材中“数学文化”的融入与分布
新课改对“数学文化”内容的重视与增加,贯穿整套教材,数学文化依托于数学史、数学典故、数学问题、数学实际应用等,在教材中以引言、探究、例题、练习、阅读与思考等方式呈现在广大师生面前. 以人教版(2019)选择性必修二第四章数列(以下简称数列)为例,笔者初步统计融入的数学文化就有34 处,详情见下表2:
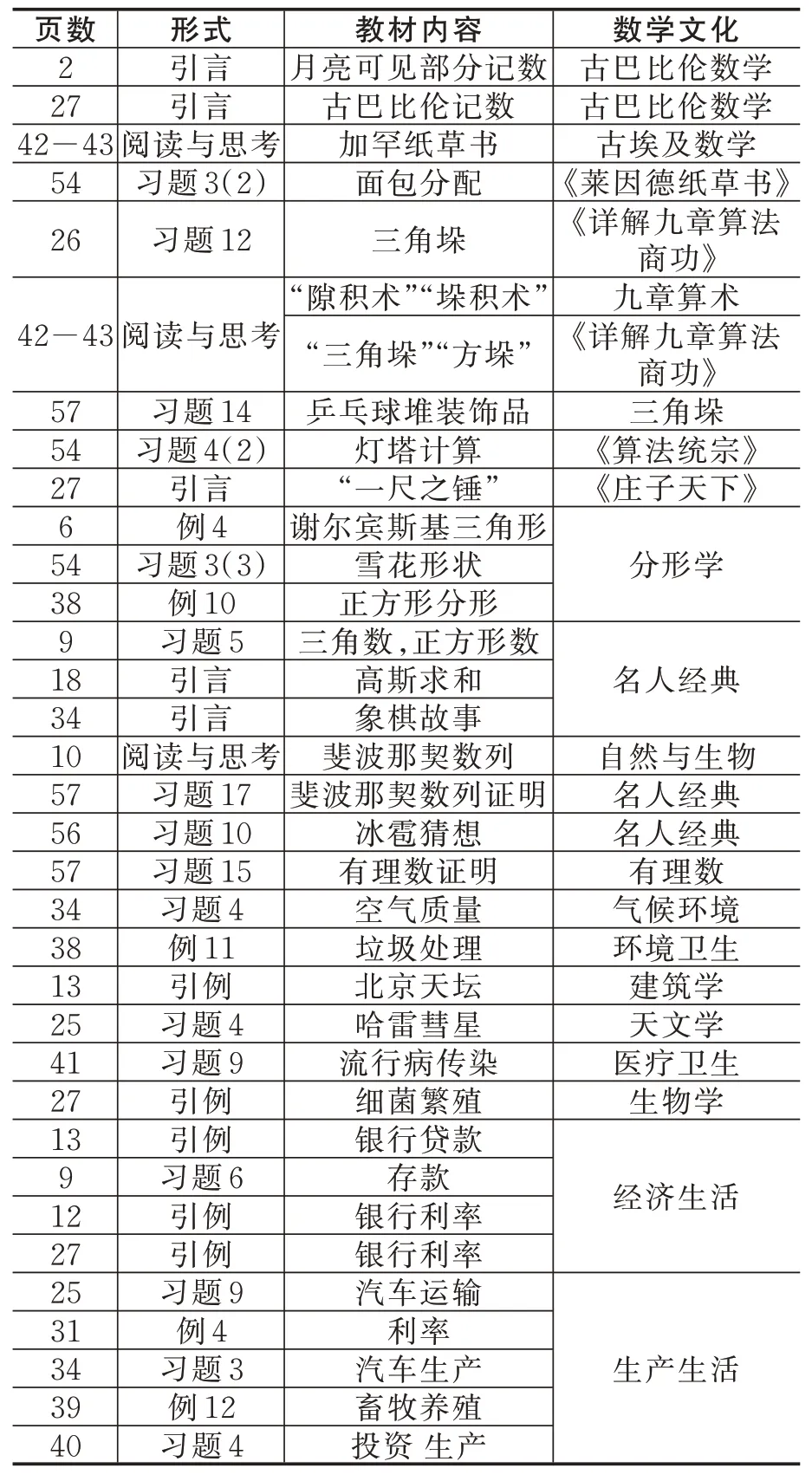
表2
如此大量的数学文化知识的融入,展现了数学的科学价值和文化价值;更也给广大教师带来了挑战. 在课时有限的前提下,如何处理教材中出现的数学文化知识,既能完成教学内容,又能提升学生的数学素养,还能较好的应对高考.
4 高考和教材在数学文化中的呼应
研究发现,数学文化在高考题和教材中通常从以下三个方面体现:
4.1 以数学史为载体,体现数学文化
数学史中有大量的古今中外的数学名著、著名的定理、公式和图论、著名的猜想、数学每个分支发展的历程……,数学史的丰富内容为命制高考题提供了丰富的资源,以数学史为背景的高考题细分为两类.
4.1.1 数学名著中的数学问题
例1(2021·全国(理))魏晋时刘徽撰写的《海岛算经》是有关测量的数学著作,其中第一题是测海岛的高.如图1,点E、H、G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”则海岛的高AB=( )

图1

这类应用问题的解决策略和教学策略在后文中详细阐述,这里不做赘述.
4.1.2 数学史中著名的定理、结论的数学思想方法和原理.
例2(2020·北京)2020 年3 月14 日是全球首个国际圆周率日(π Day).历史上,求圆周率π的方法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔·卡西的方法是:当正整数n充分大时,计算单位圆的内接正6n边形的周长和外切正6n边形(各边均与圆相切的正6n边形)的周长,将它们的算术平均数作为2π的近似值.按照阿尔·卡西的方法,π的近似值的表达式是( ).

此题蕴含的是“割圆术”中“以直代曲、无限趋近、内外夹逼”思想,把圆用两个正n 边形进行夹逼,由s2n<s<s2n+(s2n-sn)当n 无限大时,s2n→s则可估计出圆的面积s,取单位圆,则此时s值就是π的值. 无独有偶,在2017 年浙江卷第11题也出现了刘徽的“割圆术”
类似以“割圆术”作为文化背景的考题在高考题中频繁出现!如2019 年浙江卷和2013 年上海卷的“祖暅原理”;2021 年浙江卷和2007 年北京卷(理)的“赵爽弦图”;2020 年浙江卷的“垛积术”等等.
我们再来看高考题考察的深度,浅层次的考察仅套了个数学史文化的帽子. 如2017 年浙江卷的“割圆术”,即使不了解“割圆术”也可以求出正六边形的面积,2019 年浙江卷的“祖暅原理”;2007 年北京卷(理)的“赵爽弦图”;2020 年浙江卷的“垛积术”也属于此类,对于这种层次的考察,只要加强数学知识的教学即可;深层次的考察是考察数学史文化中的思想和原理. 如2020 年北京卷的“割圆术”,要用无限微分、近似替代的思想化圆面积为正六边形的面积,再用夹逼原理得单位圆的近似值,从而得π的近似值. 针对这类层次的考察,在教学中就要足够重视. 翻阅教材会发现,同时与教学内容有关的数学史在教材中都有介绍,比如上文中的“祖暅原理”、“赵爽弦图”、“垛积术”、“割圆术”等,也就是说高考中的深层次考察都是立足于教材的. 因此要重视教材中“阅读与思考”、“拓广探索”中的数学史知识,尤其是中国古代数学,可以带领学生以研究性学习的方式阅读教材中的内容,探索它蕴含的思想和原理,并对原理和方法加以锤炼.
4.2 以跨学科知识为载体,体现数学文化
文化是交融的,数学文化一方面同天文、地理、物理、生物、医药、建筑的传统学科交叉,体现数学知识的工具性,另一方面还会和新兴学科比如航空航天、电子信息、人工智能、地球信息、数据科学、分形学等交融在一起,体现数学文化的与时俱进!而高考考察也分两类.
4.2.1 各学科与数学学科交叉的知识
例3(2020·海南)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面. 在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬400,则晷针与点A处的水平面所成角为( )

图2
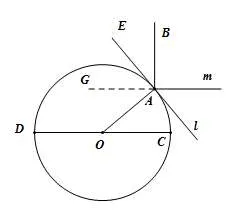
图3
A. 20° B. 40° C. 50° D. 90°
此题主要考察的数学知识是立体几何中的线面位置关系的判定和运用以及角度的计算,以古代测试间的日晷为背景,进行实物呈现,所以它还考察了数学能力中的直观想象力、抽象能力和建模能力,而学生能把实物抽象为空间图象的前提是理解地理学中的经度纬度和赤道面的知识,否则学生无法想象出球体图象,更不可能得到如图所示的截面图,此题就只有扼腕兴叹!
此外,在2021 年全国II 卷第四题“北斗三号卫星导航”中又涉及了纬度的知识,此题同样考察了有关球的位置关系的判定和角度的计算背景仍是纬度和赤道面,与2020 海南卷是何其的相似!事实上,人教A 版(2019)必修第一册第256页的“拓广探索”第27 题已明确提到地球公转过程中太阳直射、地球纬度问题,若在此处重视一下纬度知识,锻炼学生实物与空间几何图象的转化,空间图形与平面图形的转化,那么此类高考题解决的就会较为轻松.
4.2.2 分支学科所蕴含的思想原理和方法
例4(2021·全国)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折,规格为20dm×12dm 的长方形纸,对折1 次共可以得到10dm×12dm,20dm×6dm 两种规格的图形,它们的面积之和S1=240dm2,对折2 次共可以得到5dm×12dm,10dm×6dm,20dm×3dm 三种规格的图形,它们的面积之和S2=180dm2以此类推,则对折4 次共可以得到不同规格图形的种数为 ;如果对折n次,那么
此题貌似民俗文化背景,通读完题目后就会发现此题具有明显的迭代递归、自相似的特征!这恰是分形几何学的基础!目前分形理论广泛应用于各个领域,从物理学到地球物理到地质地貌、从化学到生物学到医学、从计算机科学到工程技术学、从艺术设计到人文社科、甚至改变了传统的维度的划分!对于像这样的新兴的、对社会影响巨大的学科,教材和高考都会有所涉及,以体现知识的与时俱进,激发学生的创新精神!
比如在数列中就把“谢尔宾斯基三角形”(以下简称“谢三角形”)作为典型例题编入教材,“谢三角形”是很有代表性的线性分形,具有严格的自相似特点,是分形几何学中一个经典的例子,不仅如此教材第38 页的例10“正方形分形”和第55 页练习题“瑞典数学家科赫的雪花形状”又是经典的分形问题.

如果我们教师在此教学时对教材的典例研究它们的共性,引导学生寻找迭代,发现规律,进行方法原理上的锤炼,甚至拓展一下介绍“分形学”在人文社科、自然科学中的发展,不但可以加深学科知识的掌握应对高考;还可以拓宽学生的视野,以数学的目光看世界,提升学生的数学素养!
4.3 以数学应用为载体,体现数学文化
随着国家对学生应用意识、应用能力的日益重视,高考卷中体现学生解决日常生活中的实际问题的试题不断呈现. 这类命题通过设计合适的试题情景把生活中的方方面面融入数学,如:营销策略、经济生产、环境保护、医疗卫生、军事科技、建筑测量、生活服务、概率统计等等. 从知识能力角度:它体现了数学建模思想,考察学生的阅读、抽象、转化与化归、实践等能力;从情感角度:培养了学生的社会意识和创新意识,让学生感受知识来源于生活服务于生活.
教材中随处可见各种文化背景的数学应用题,以“数列”为例,从第1 页至第43 页,先后编入了15 道数学应用题(见表2),在2021 年的高考真题中仅涉及数列知识的实际应用题就出现3 处.
例5(2021 年上海)某公司从2021 年第一季度开始,第一个季度的营业收入1.1 亿元,利润0.16 亿元,后面每一季度比前一季度营业收入上涨0.05 亿元,利润比上一季度多4%;(1)求到2025 年总共20 个季度的营业收入之和.(2)从哪一年哪个季度起,利润超过营业收入的18%.
本题两个对象,“营业收入”构成一个首项为1.1,公差为0.05 的等差数列{an} ;“利润”构成一个首项为0.16,公比为4%的等比数列{bn} . 然后本题的第(1)问就转化成了等差等比数列的分组求和问题,第(2)问转化成解指数不等式问题. 对比教材“数列”内容:
例6(教材“数列”第38 页例11)去年某地产生的生活垃圾为20 万吨,其中14 万吨垃圾以填埋方式处理,6 万吨垃圾以环保方式处理. 预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5 万吨,为了确定处理生活垃圾的预算,请写出从今年起n年内通过填埋式处理的垃圾总量的计算公式,并计算从今年起5 年内通过填埋方式处理的垃圾总量.
同样提取信息可知:每年生活垃圾的总量构成等比数列{an},每年以环保方式处理的垃圾量构成等差数列{bn},每年以填埋方式处理的垃圾量构成数列{cn},cn=an-bn,因此仍是利用等差、等比数列的知识进行计算,它们蕴含的文化背景不同,考察的能力和数学知识是一致的.
对此类数学文化问题的教学重点在于培养学生的阅读能力和抽象概括能力,锻炼学生提取关键信息,建立关联,归纳到相关数学知识上.
5 结语
《考纲》与《课标》必然互为呼应,高考立足于教材又高于教材,“立足于教材”体现在高考中的数学文化都分布在教材的每一行每一页,而“高于教材”则需要运用我们学习到的数学知识、原理、思想以及锤炼出的数学能力来解决问题!所以日常教学要钻研教材,运用大单元教学整体把握思想原理和知识脉络,提升学生的数学素养.
