基于分类思想 整合教材练习——以《平行四边形性质2》为例

广东省深圳市光明区实验学校（集团） 钟文波 （邮编：518132）

1 引言

随着数学新标的不断发展，教师对课堂更加注重优质、高效，自然，对教材的质量也提出了更高的要求，对教材进行有效的整合是教师提高课堂效率的重要手段之一，也是教师教学中“创造性教学”行为.《义务教学数学课程标准（2011 年版）》指出：“教材的编写要有利于调动教师的主动性和积极性，有利于教师进行创造性教学”. 教材是教学活动中的一种重要的资源，教师应该克服对教材一味的崇拜与依赖，要从“教教材”转变到“用教材教”，凸显教师的主动性，根据学生学习水平和心理特征等实际情况，因材施教，适当替换、删减、补充、重组、调整相关内容，特别是教材中例题和习题. 有时教材中的习题比较零散，系统性和整体性没有预期中的效果，常常会影响课堂质效，教师可以用分类思想整合习题，这样让学生更能系统地、整体地应用知识，提高学生的数学核心素养. 笔者就以北师大版八年级下册《平行四边形性质2》为例，谈谈运用分类思想，整合教材中的练习.

2 教材整合内容

2.1 基本内容

在上一课时的“做一做”中，我们发现:平行四边形的对角线相互平分，请尝试证明这一结论[2].

已知：如图1，▱ABCD的两条对角线AC与BD相交于点O.

图1

求 证：OA=OC，OB=OD.

你还有其他证明方法吗？与同伴交流.

定理平行四边形的对角线相互平分.

2.2 基本习题

例如图2，在▱ABCD中，对角线AC与BD相交于点O，过点O任作一条直线分别交AB、CD于点E、F．

图2

求证：OE=OF.

做一做 如图3，▱ABCD的对角线AC与BD相交于O，∠ADB=900，OA=6，OB=3.求AD和AC的长度.

图3

平行四边形性质2 是北师大版的八年级下册第六章第一节第二课时内容，主要是探索并证明平行四边形对角线相互平分的性质，并进行平行四边形的简单应用. 而在人教版教材中，平行四边形对角线的性质是人教版的八年级下册第十八章第一单元第一课时内容，主要也是探索并证明平行四边形对角线相互平分的性质，并应用性质解决相关问题，所以笔者在整合教材时，保留了探索并证明平行四边形对角线性质，而对例题和习题进行归类，再系统地分类，形成了利用平行四边形的对角线性质解决线段问题、周长问题、面积问题三大类应用，对面积中的一般性规律也进行了总结，得出以下结论2，并适当延伸拓展，把平行四边形性质内容巩固深化，具体整合内容如下：

2.3 教材整合优化

例1已知：平行四边形ABCD的两条对角线AC与BD相交于点O.

求证：OA=OC，OB=OD

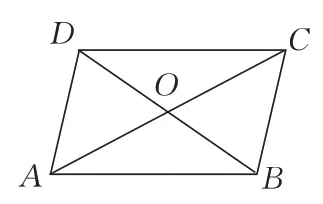
图4

分析学生根据上一课时探究出的平行四边形对边相等，以及平行四边的定义，会有两种证 明 方 法：（1）ΔAOD≌ΔBOC；（2）ΔAOB≌ΔCOD，从而证出AO=OC，OB=OD，由此证出平行四边的对角线的性质：

结论1平行四边形对角线相互平分.

教学说明上一课时学生已经探索出了“平行四边形的对角线”的性质，学生已经猜想到结论，但缺乏演绎推理，通过文字语言直接转化为数学的几何语言，让学生清晰明了相关知识点，并让学生思考、表达自己证明的思路，鼓励学生选择多种方法进行证明，完成合情推理到演绎推理的过程.

教材中的例题和习题主要是平行四边形性质的应用，但相对比较琐碎零散，针对此情况，笔者对平行四边形的应用进行了整合和深一步挖掘，把平行四边形性质的应用分为：线段问题、周长问题、面积问题三类问题，采用分类讨论思想，更加深刻地、系统地解决平行四边形性质应用问题，提高学生的数学核心素养.

3.1 线段问题

3.1.1 用整体法求解

练1如图5，点O为▱ABCD的对角线AC、BD的交点，且AO+BO=11，则AC+BD= .

图5

分析学生根据平行四边形的性质不难得出：，即AC+BD=

教学说明此题学生由平行四边形的性质容易得出AC、BD与AO、BO的数量关系，再用整体法求算出结果，教师在学生在求解过程中，渗透整体法思想，提高学生的数学核心素养.

3.1.2 用勾股定理思路求解

练2如图6，在▱ABCD中，AC、BD相交于点O，AB=10cm，AD=8cm，AC⊥BC，则OB= cm.

图6

分析学生根据平行四边形的性质得由勾股定理得从而得到：OC=

教学说明在八年级阶段，学生在求线段的长度问题时，常常利用勾股定理，教师可以适当引导学生用勾股定理思路，同时让学生思考并表达自己的想法，让学生积极参与到课堂中来.

3.2 周长问题

3.2.1 用整体法求解

练3如图7，▱ABCD的周长为20cm，AC、BD相交于点O，OE⊥BD交CD于E，则△BCE的周长为 cm.

图7

分析学生由平行四边形的性质可知：BO=DO，又OE⊥BD，即OE垂直平分BD，得出DE=BE，所以△DCE的周长为：BC+CD=

教学说明周长问题本质上是线段问题，引导学生把周长转化为线段问题，即BE可以换成DE，△BCE的周长就是BC+CD，再用整体法得出结果. 通过此分析反推就可以得出结果，让学生感受逐级分解目标、分析推理过程，体会反向推理的魅力，提高学生的推理能力.

3.2.2 用全等思路求解

练4如图8 所示，在平行四边形ABCD中，对角线AC与BD相交于点O，过点O任作一条直线分别交AB、CD于点E、F．

图8

（1）求证：OE=OF；

（2）若AB=7，BC=5，OE=2，求 四 边 形BCFE的周长．

分析学生由平行四边形的性质易，从而得到（1）；C四边形BCFE=BE+BC+CF+EF=DF+BC+CF+2OE=CD+BC+2OE=16.

教学说明此题是教材中例题和习题的整合，采用的一题多问的形式，涵盖了线段问题和周长问题，是平行四边形性质的综合应用，有效地解决了例题与习题分裂问题，系统地处理了平行四边形性质应用问题.

3.3 面积问题

3.3.1 总结规律

例2如图9，平行四边形的两条对角线将平行四边形的面积分成四部分，分别记作S1，S2，S3，S4，则它们之间的大小关系是 .

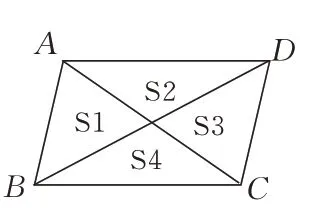
图9

分析学生易证S1=S3，S2=S4，而S1和S2是同底等高，得到S1=S2，即S1=S2=S3=S4.

教学说明在推理平行四边形对角线相互平分的过程，学生已经推出了S1=S3，S2=S4，进一步引出问题：S1和S2有什么关系？学生通过分析，能得出它们是同底等高的三角形，推出S1=S2=S3=S4，引导过程循序渐进，层层梯进，得到下面的结论自然就是水到渠成！

结论2平行四边形的对角线把平行四边形的分成四个面积相等的三角形.

练5如图10 所示，在▱ABCD中，AD⊥BD，AD=4，DO=3． 则△COD的 面 积是 ．

图10

分析学生由平行四边形的性质可知：BD=2DO=6，而AD⊥BD，即S▱ABCD=AD·BD=24.

教学说明此题是结论2 的应用，学生通过练习巩固了新知内容，达到学以致用的效果，同时让学生加深了对平行四边形性质的理解，换角度换方法理解性质，学生也更加全面地了解了平行四边形的对角线的性质.

3.3.2 拓展延伸

延伸1如 图11，P为平行四边形内任一点，△PAB、△PBC、△PCD面积分别为3，4，5，则△PAD的面积为 .

图11

分析学生通过观察P不是对角线的交点，不能用结论2解决，这时学生想到要回归到面积的公式，容易想到作高，过P点作PM⊥AB，PE⊥AD，如图12，并反向延长MP、EP交CD于N和F点，易 证MN⊥CD，EF⊥BC. 则SΔPAB+同理可证：SΔPBC+，即可算出SΔPAD=4.

图12

教学说明此题是结论2 的拓展延伸，由平行四边形的对角线交点O改变为一般的P点，从特殊到一般，有部分学生可能猜到了结论，但引导学生理论证明，让学生理性地回归到三角形求面积公式，学生不难得出需要作高，从而解出此题，让学生体会从合情推理到演绎推理质飞跃的过程. 此题主要是让学生独立思考并表达自己的求解思路，提高学生的表达能力和挑战精神，教师及时鼓励表扬，使学生体会到成功的快乐.

延伸2如图13 所示，一个平行四边形被分成面 积 为S1，S2，S3，S4的四 个 小平行四边形，当CD沿AB自左向右在平行四边形内平行滑动时，S1·S4与S2·S3的大小关系为 .

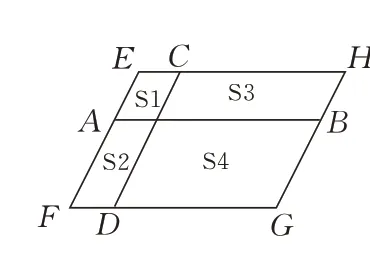
图13

分析学生根据上面一题能想到作高求面积，如图14，过C作CN⊥FG交AB于M点，易证CM⊥AB，S1·S4=CM·AP·MN·PB，S2·S3=MN·AP·CM·PB，从而得到S1·S4=S2·S3.

图14

教学说明延伸1 到延伸2 是三角形面积问题到四边形面积问题，进一步得到延伸应用，思路层层递进，让学生领略更广的一般性规律，同时注入了线段移动的条件，让学生在动中找不动，使学生体会数学中的动中有静，激发学生对数学的学习兴趣，提高学生学习积极性.

4 教材整合反思

基于分类思想，通过系统地对知识内容和习题进行分类整合，让学生能更加整体性掌握知识点，促进学生有条不紊地分析并解决问题，无形中也渗透了数学分类思想，提高了学生的数学核心素养. 其实，教材的整合不是简单的删减和拼接，也不是简单的替换和补充，而是教师根据学生学习水平和认知水平进行的有效整合，也是因材施教教学的体现.

4.1 整合要尊重课标的基础性

通过整合，本课时的内容主要还是探索并证明了平行四边形的性质定理：平行四边的对角线相互平分，且通过练习以及延伸，加深了对平行四边性质定理的理解，也发展了学生的应用意识，这些都是围绕着课程标准内容展开的. 教材编写和教材整合都应该以课程标准为依据基础，所有教材整合都要以课程标准为核心，只有在课程标准的框架下，开展教材的整合才会有实质性的效果.

4.2 整合要注重学生的主体性

本课时体现了学生是数学学习的主体，通过学生讲解自己的求解过程，让学生在积极参与学习活动的过程中发展了学生的语言表达能力；通过学生上台板演活动，让学生在几何书写过程中提高了学生的逻辑思维能力. 注重了学生对基础知识、基本技能的理解和掌握，整合之后，有平行四边形性质的基础练习应用，也有性质的拓展延伸，注重了知识的“生长点”与“延伸点”，让学生体会对知识内容可以从不同的角度加以分析、从不同层次进行理解. 在本课时中，教师主要采用设问引导式教学，充分发挥教师是学生学习活动的组织者、引导者、合作者的作用，教材的整合要体现“以人为本”的理念，重视学生的主体性，促进学生全面发展.

4.3 整合要符合学情的顺序性

根据课程标准要求，教材编写和教材整合“要符合学生的认知规律”，这要求在教材整合过程中，知识内容和练习应用都要符合学情的顺序性和学生认知情况，本课时不管是性质练习应用，还是拓展延伸，都是学生用已有的知识可以解决，并在旧知的基础上构建新知体系. 教材的整合是人性化，不具有普遍性，要从学生实际情况出发，遵循学情的顺序性，因地适宜地进行开展.