指向课堂建构的教学设计示例——透过“数轴概念”的视点

淮北师范大学数学科学学院 张 昆 （邮编：235000）

在发生认识的心智活动中，研究者从各自的观察立场、视点、对于观察对象的个性特点的心理预期等出发，提出了一系列学习理论：例如，“目的－手段分析”或“有目的探索”；“突然理解”或“顿悟”；“方法与目的之间的协调”等；其中，皮亚杰引入认识图式的概念，解释发生认识的心理活动过程，知识的发生与发展归结为两方面：其一，知识形成需要一个心理结构（图式）；其二，知识发展过程中的新知识具有符合知识特点的心理形成机构. 整合图式与合乎新知识特点的心理形成机制，构成了建构主义学习理论的基础.

1 建构主义学习理论的内涵

皮亚杰使用了一组四项递进的概念：图式、同化、顺应（有翻译成顺化）和平衡，用以说明发生知识认识心智过程中的建构活动. 其中的图式概念，指的是动作（在没有建立起逆运算的婴儿期，孩童不能进行运算）或运算（六、七岁年龄段的学龄前的儿童，建立起了逆运算）的内在心理结构，这是人类发生知识认识的心理工作台，也是学习主体已经通过学习掌握了需要发生新知识的素材的仓库，即外在信息就是在图式中进行锻造加工的，同时图式还提供了学习主体已经掌握了的发生新知识认识的部分素材. 因此，图式构成了发生新知识认识的物质载体[1].

同化指的是学习个体将外在现象中的学习素材（信息）纳入自己已经形成的图式之中，于是，信息经由图式的过滤与选择，因此，将外在信息刺激输入的过滤、选择与改变称为同化. 凭此，能够认识到，同化只能引起学习主体的图式的量的变化，因为它同化信息时，无须改进或完善已经形成的图式，就足以应对现象性信息.

顺应指的是当学习主体面临外在信息时，目前所具有的图式无法直接同化外在具体特点的信息，从而为了发生知识认识，学习主体就必要依据外在信息特点，自己经验中成功地同化某些程度上具有相似特点的信息的那个具体图式，加以改进与完善以适应面临的外在信息特点，从而创造出适合于新信息特点的新的图式，如此发生知识认识.

平衡概念，指的是同化作用与顺应作用两种技能的平衡. 这种平衡具有自我调节的意义，学习主体以一系列的主动补偿作用来反应同化与顺应两者之间的相互作用.

同化、顺应与平衡的整合作用构成了图式这一工作台工作活动、发生知识认识的操作方式与行为活动. 学习主体在发生知识认识时，总是首先使用原有图式进行同化，如获得成功，便得到了暂时认识上的平衡；如果同化不成功，学习主体便要作出顺应，选择与调整原有图式或创造新图式去同化外在信息，由此认识到，发生知识认识的最初源头应该归结为认识结构的同化作用，直至达到认识上的新的平衡为止[2].

这几个概念构成了建构主义学习理论的基础. 建构主义学习理论认为，学习主体面临外在信息时，如果内部图式没有依据外在信息特点的经验，外在信息就是毫无意义的信息碎片、星星点点、一盘散沙，无意义的碎片信息是不可能发生知识认识的，要想发生知识认识，就需要首先通过利用认识结构，即图式中曾今同化过与外在信息特点相类似的信息，赋予外在信息以意义，达到同化外在新信息的目的，从而发生知识认识.

将学习主体利用图式赋予外在新信息以意义的过程称为建构，以建构为基础的发生知识认识的心理过程的理论，称为建构主义学习理论.

2 数学课堂教学中学生建构活动的主要特点分析

学生发生数学认识是由认知方面、情感方面与社会方面协同作用的结果，认知方面提供了建构的平台与相关材料（包括学生通过过去的学习已经掌握了的知识、观念与方法等；还包括通过及时感知外在信息等）；情感方面提供了学生发生数学知识认识的心理动力（内驱力）；社会方面（包括两方面，一方面，通过数学史、数学文化等，这是通过教科书提供的语言，据此形成与过去的数学家进行交流；另一方面，课堂教学现场中的同学之间、师生之间的交流），前者提供了数学规范（例如相关的数学知识规定的表述，如特定的符号或其他语言）与格式；后者由于课堂的生成，提供了课堂教学活动的素材与动力. 因此，学生发生数学知识认识的构建活动具体递进的且相互依赖的几项特点：

其一，个性构建. 建构主义学习理论特别注重学生发生新知识认识时所选择使用的图式（后面一律称为认识结构）的特点，很显然，对于班级授课制来说，不同的学生对于呈现于自己面前的信息，由于他们的数学现实与生活经验不同，具有不同的认识与理解，进而选择具体图式，将信息构建出不同的个性意义，因此，这种建构活动明显地具有个性特点. 即当数学教师（或教科书）提供或者学生自己发现新信息时，不同的学生对于信息产生的认识结果，不是千篇一律的，应该处于从现象到本质的各种不同层次的水平上，这就构成了个性建构的特点.

在教学设计及其课堂实施中，数学教师要特别注意启发学生进行个性建构所得到的结果，这是每名学生基于自己的基础（特定的认识结构，即图式与数学现实），赋予新信息以具体意义的心理活动过程，当学生需要顺应才能建构信息形成轮廓时，就会充分地体悟到建构时思维的创造性. 在个性建构活动中，不同的学生可能对于同一种信息产生了不同的理解，赋予不同的意义，这些不同的理解与赋予不同的意义，在班级中，就会造成了一种竞争的态势，这为学生营造了非常好的学习氛围，学生在提出自已的理解，即赋予信息以自己的意义，就会为自己的意见与想法辩护，通过学生之间或师生之间进行充分交流，一定会帮不同学生深入理解信息，揭示信息所组成结构的本质形成心理内驱力.

其二，共同体建构. 在发生数学知识认识时，对于呈现于学生面前的信息，班级中的不同学生经由个性建构，一定会出现深深浅浅的理解及其比较准确或比较不准确的结果表达，这种不同的理解及其结果表述，作为教学素材，对于教师所进行的课堂教学非常重要. 首先，不同学生产生的不同理解的结果，一定会具有创造性，即使产生的理解是错误的、表示可能是非常不准确的，但是，这些生成性的素材，构成了学生发生数学知识认识、理解新知识产生的基础，即最终学生发生知识的正确认识一定蕴含于这种个性建构的素材之中；其次，重要的是，教师要想方设法将这种个性构建及其成果，转化为共同体建构的素材与基础.

共同体建构的素材来源在于个性建构所形成的结果，数学教师要对个性建构的结果即兴地进行评估，将这些个性结果形成等级层级，然后，帮助学生理解这种将个性建构结果划分等级层次的活动过程，从而启发学生经历将这些个性建构内容去粗取精、去伪存真，由此及彼、由表及里的改造制作功夫[3]，这是一种协调的过程，在这种协调过程中，学生理解他人的观点、方法，发生数学知识认识，从而帮助学生构成数学知识的尽可能准确的表述，这种表述尽可能接近课本上提供的内容，但是，终究不可能形成完全等同于课本上的表述. 这就是从个性构建过渡到共同体建构，共同体建构将会更接近那个数学知识点的本质及其表述.

其三，文化规范. 对于个性建构的结果内容，虽然经由共同体的建构，即将通过个性建构内容的协调与整理，形成的比较准确的结果内容，但是，大多数情况下，这些内容的表述可能与课本提供的内容，还存在着或多或少的差距. 此时，就需要历史文化中经由数学家长期的选择、调整与修正，形成的字斟句酌进行表述的数学知识点，学生最终必须要使用这种文化规范的表达的结果来武装自己，因此，就为帮助学生与数学共同体（数学家的表述内容）的交流打开了通道.

这是因为，直接由文化规范表述的知识结论，通过社会化的方式的传递，学生也可以进行学习的，而且低年级大多数知识认识活动，基本上都可以通过社会上人与人（包括教师与学生）之间的互相作用，即通过社会传递帮助学生完成学习任务. 其实，社会化是一个结构化过程，学习数学的个体对社会化所作出的贡献，正如他从社会化中所得到的同样多，从“个性建构”过渡到“共同体建构”的协调过程的特点出发，就能够认识到，“个性建构”与“共同体建构”过程，其实是学习个体与班级的一种相互交换的过程，对于数学课堂教学来说，这种交换是特别重要的.

其中，最为重要的是“个性建构”. 这是因为，作为社会性的知识传递，能够直接从文化规范了的数学知识出发，传递给受教育者，帮助学生完成学习的任务，如此，就能够绕过发生数学知识认识的“个性建构”与“共同体建构”这两个重要环节. 对于学校数学教育教学来说，教师稍有不慎，就有可能选择采用这种传递文化规范的方式进行教学活动. 这就会极大损伤数学知识的教育教学价值，泯灭学生学习积极性、热情与兴趣，长期以往，最终会导致学生放弃数学学习.

总之，在数学教学设计及其课堂实施的活动过程中，也可以绕过“个性建构”与“共同体建构”这两个重要环节，直接使用文化规范所形成的数学知识表述传递给学生，但如此教学将损伤数学知识的教育教学价值.

3 指向课堂建构的教学设计示例

陆游诗云，“纸上得来终觉浅，绝知此事要躬行”；《增广贤文》曰，“理在用中方识妙，事非经过不知难”. 虽有至善的数学教育教学理论，如果不将这些数学教育教学理论运用于数学教师的教学实践中去，那么数学教育教学理论就会尽显苍白，失去力量，数学教育教学实践也不得不在具体数学教学活动中不断地摸索[4]. 这里，以“数轴概念”教学为例，加以必要说明.

师：有理数的组成：负有理数；零；正有理数.

师：向大家提出一个问题：能够用一直线上的点表示所有有理数吗？

生1：负数、正数无限多，零只一个，在MN上任取一点O，规定它表示零（如图1）.

师：这个点O在直线MN上具有非常重要的作用，大家如何给它起一个名字，这个名字叫什么好呢？

注学生给这个点O取了许多名字，如“中点”“点”“元点”等，笔者必须要说明历史上的数学家通过不断地选择、完善与修订，最终将这个点O称为“原点”. 这里，就经过了“个性建构”、“共同体构建”与“文化规范”的过程.

师：点O将直线MN分成三部分，自身表示有理数0，称点O为“原点”. 负、正数该由射线OM，或射线ON（除端点O）上的点表示. 究竟哪一条射线上的点表示正有理数呢？

师：这些方案中，那种更简单、更实用？

生：用箭头！

师：在图1 的直线上，添加一个箭头. 约定用具有箭头的射线上的点表示正数；反之，表示负数. 称“箭头”为“正方向”.

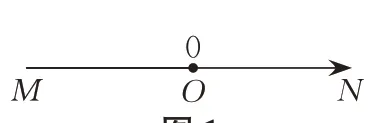
图1

注学生想出了区分哪一条射线表示正有理数与负有理数的许多标志. 例如，“规定原点右方的射线表示正有理数，则原点左边的射线表示负有理数”；“染色，将染成黑色的射线表示正有理数，染成红色的射线表示负有理数”等等. 笔者通过调整直线段方向形态，否定了前一种方法；以染色操作太复杂否定了后一种方法；学生的其他方法也不太好. 直到学生想到了在一条射线上打上一个“箭头”为止. 笔者使用文化规范，告诉学生这个“箭头”成为“正方向”. 很显然，这种鼓励学生建构的活动经过了“个性建构”、“共同体建构”与“文化规范”的过程.

师：如何在图1 上表示+2？

注课堂主要活动记录：如图2，两同学分别选择点A和点B，都声称要表示+2. 这就出现了新问题.

图2

师：哪一个才是真正表示+2 的点？

注学生想出了许多方法用以确定表示有理数+2 的那个点，如图3，学生决定用一把“尺子”裁决，以原点O为起点，在具有正方向的那条射线上次第量两尺，规定“尺子”落脚的终点C为表示+2 的 点，而A和B都不是 表示+2 的点.

图3

师：“尺子”是一个度量长度的单位，称之为“单位长度”.

注这里的“尺子”是借用生活语言的一种个性建构或共同体建构的表述，需要使用文化规范中的字斟句酌的表述，就是“单位长度”.

师（利用文化规范进行总结表述）：当在一条直线上约定了“原点”“正方向”与“单位长度”这三个关键性的要素后，这条直线就可以表示所有的有理数了. 于是，规定了原点、正方向和单位长度的直线叫数轴.[5]

笔者在教学设计及其课堂实施时认识到，只有帮助学生理解了数轴三要素“原点”“正方向”“单位长度”的功能及其协调发挥，才能促进学生从整体上认识与理解数轴概念. 在分析数轴概念这个知识点时，教师必须要认识到数轴作为一项工具的功能，建构这一工具的目的，都只是为了在一条直线上表示所有的有理数（更进一步理解是使用一条直线上的点表示所有的实数），从而使有理数（或实数）达到“可视化”的目的，因此，这节课所选择的引入情境，就是讨论“如何在一条直线上表示有理数？”这一初始问题[6].

在这个初始问题的促动下，笔者通过启发学生研究有理数分类的“三分法”特点，鼓励学生在这条已知直线上一步一步地建构出了“原点”、“正方向”与“单位长度”这“三要素”，学生经由亲身的建构活动过程，理解了“三要素”各自的不同功能. 将这“三要素”的功能整合起来，促进学生理解了数轴概念的功能，进而理解了数轴概念.课堂教学的策略在于，对“原点”“正方向”与“单位长度”这“三要素”次第采用了“个性建构”“共同体建构”与“文化规范”的建构顺序，并且通过整合的这三项建构的心理活动，最终发生了数轴概念的认识.

4 结束语

学习主体任何数学知识的发生，最终都是认识结构同化作用的结果. 这种同化作用的过程就是将面临发生具体数学知识认识的外在现象性信息进行组织，即选择认识结构、即图式形成某种有意义的轮廓的过程，这就是认识结构的建构过程. 在班级教学中，这种建构活动存在三种不同层级的递进方式：一是个性建构，二是共同体建构，三是文化规范（其实历史上经由成功建构而形成的字斟句酌的结果表述），课堂教学活动过程的特点在于，必须要体现这三种层次构建的整个活动过程.