基于数学自然性的问题情境设计与分析
2022-06-27安徽省六安市霍邱县教育局教研室李永林邮编237400
安徽省六安市霍邱县教育局教研室 李永林 (邮编:237400)
安徽省六安市霍邱县第一中学 梁 松 (邮编:237400)
数学的自然性是指数学知识发生发展的内在逻辑必然性. 普通高中数学教材主编刘绍学在《主编寄语》中指出:数学是自然的[1]. 事实上,数学核心素养的形成与发展,数学概念的形成,数学对象的研究思路探寻,数学问题的解决方法产生都是自然的.
数学教学需要遵循自然性原则. 基于数学自然性的教学,有利于学生提高学习数学的兴趣,增强学好数学的信心,理解数学本质,训练科学思维方法. 然而,在实际教学中,数学的自然性并没有得到足够的重视,依然存在“重结果,轻过程”、“重怎么做,轻怎么想”等现象.
如何将数学的自然性体现在实际教学中,教师需要深度思考知识的发生发展过程以及它们之间的相互联系,要在立足学生认知基础、遵循学生认知规律的前提下,设计自然而然的问题情境,并以之为载体,有序开展教学活动,让学生从中感受到问题的发现和提出途径是自然的,问题的分析和解决过程是自然的.
下面,以初中数学教学为例,从四个方面阐释基于数学自然性的问题情境设计思路.
1 创设自然而然的问题情境,促进学科核心素养发展
数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析是数学学科的六大核心素养,它们是在数学学习和应用的过程中逐步形成和发展的. 以沪科版九年级数学上册《23.1 锐角的三角函数》中关于“如何刻画坡度?”内容教学为例,通过设计如下自然而然的问题串,推进教学,形成并发展学生数学学科核心素养.
问题1(展示图1 和图2)汽车爬坡能力是衡量汽车性能的重要指标之一,汽车爬坡能力是指汽车在满载时所能爬越的最大坡度,图中两辆汽车都在爬坡[2]. 你能画出几何图形表示爬坡过程中汽车的位置变化吗?你能比较图中两坡的陡缓程度吗?请说明.

图1

图2
问题2你能比较图3 和图4 两坡的陡缓程度吗?(图中数字表示长度)

图3

图4
问题3你能比较图5 和图6 两坡的陡缓程度吗?(图中小写字母表示长度)

图5

图6
问题1 从学生生活实际(汽车爬坡)和已有基本活动经验(坡的陡缓程度与坡角的关系)出发,让学生感受到数学源于生活,并应用于生活.学生从实际情境中抽象出几何图形,直观获得“爬坡过程中,汽车既水平前进,又铅直上升”和“对于水平前进同样距离,坡若越陡,汽车铅直上升就越高”等结论,发展数学抽象、数学建模和几何直观等核心素养.
问题2 是对问题1 的定量分析,当水平距离相等时,比较坡的陡缓程度,只需比较铅直上升高度大小,这是学生通过问题1 的解决,形成的已有认知. 当水平距离不相等时,如何比较坡的陡缓程度?解决这一问题,需要引导学生立足已有认知,紧盯“化未知为已知”目标,深入思考,让学生自然而然地想到,利用相似形知识,将其转化为“水平距离相等时,比较坡的陡缓程度问题”,培养学生化归思想,发展逻辑推理核心素养.
问题3 是对问题2 的一般化推广,发展学生的逻辑推理核心素养. 实际上,在问题2 解决的基础上,问题3 可解决如下:
如 图7 和8,在AC和A1C1上 分 别 取 点M和M1,使得AM=1,A1M1=1,过M作AC的垂线,交AB于点N,过M1作A1C1的垂线,交A1B1于点N1.
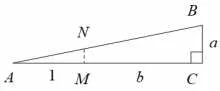
图7

图8
比较两坡的陡缓程度,即比较线段MN和线段M1N1长度,易得△AMN∽△ACB,△A1M1N1∽△A1C1B1,由相似三角形性质可得
学生解决了问题1、2、3,经历了完整的数学建模过程,发展数学建模核心素养.
2 创设自然而然的问题情境,促进数学概念形成
数学概念是关于某一类数量关系和空间形式共同本质属性的表达. 它们的形成都有自然背景,数学概念教学要让学生明确这个自然背景,只有弄清“概念从哪里来?”、“为什么学概念?”和“概念是什么?”的问题,学生才会感受到概念的形成是自然的,才能真正理解概念的本质. 下面以沪科版八年级数学上册《函数》概念教学为例,阐述如何遵循自然理念.
教师在设计函数概念教学时,应借助学生在函数方面的已有认知(第一学段(1-3 年级)的“探索简单的变化规律”,第二学段(4-6 年级)“正比例、反比例”及“探索给定情境中蕴含的规律和变化趋势”等.),设计如下问题串:
问题1已知长方形的长为a,宽为b,面积为S.
(1)若a=2,那么S与b成正比例,还是成反比例?对于S、b这两个量,给出其中一个量,你能求出另一个量吗?结果唯一吗?
(2)若S=2,那么a与b成正比例,还是成反比例?对于a、b这两个量,给出其中一个量,你能求出另一个量吗?结果唯一吗?
问题2现实生活中,有很多变量,它们之间的关系很微妙,值得我们去研究,请思考并解决教材中的问题①、问题②、问题③.(问题①:热气球上升海拔高度与上升时间关系表;问题②:用电负荷曲线;问题③:汽车制动距离与车速之间的关系式.)
问题3请思考,上述问题①、②、③中的两个量是怎样变化的?有什么共性?
问题1 的设计意图是让学生在已有认知基础上,感受即将研究的对象是小学所熟悉的知识,解决“函数从哪里来的?”的问题.
问题2 的设计是结合生活实际,利用表格、图象、表达式刻画两个变量间的依附关系,目的是让学生真切感受到正在学习的内容是有用的,解决“为什么要学函数?”的问题.
问题3 的设计是让学生感受数量的变化过程,以及两个变量之间的依附关系,通过数学抽象,获得函数的概念,解决“函数是什么”的问题.
3 创设自然而然的问题情境,促进数学对象的研究思路探寻
数学学习离不开对数学对象进行研究,要促使学生自主、深度参与到数学学习中去,就必需创设自然而然的问题情境,帮助学生构建研究数学对象的路径,让学生明白研究数学对象是有“套路”的. 以沪科版八年级数学下册《19.2 平行四边形》教学为例,设计如下自然而然的问题串,促进数学对象的研究思路探寻.
问题1有关三角形的知识,我们学过了哪些?
问题2观察图9 中的图片,从图片中你发现了哪些几何图形?请画出来. 判断所画的图形是不是平行四边形?若不是,请说明原因. 根据你的判断,试着给出平行四边形的概念.

图9
问题3类比三角形,平行四边形有哪些基本元素?观察图形,猜想一下,这些元素本身具有什么性质?它们相互之间有什么样的关系?
问题4(列举出学生猜想出来的结论)这些结论是正确的吗?若是,请证明;若不是,请举出反例.
问题5能证明正确的结论就是平行四边形的性质,类比等腰三角形性质和判定定理之间的关系,你能写出平行四边形的判定方法吗?
问题6你写出的这些判定方法是正确的吗?若是,请证明;若不是,请举反例.
问题1的设计,虽然在知识方面,三角形与要研究的平行四边形关系似乎不大,但在研究的方法和思路上是类似的,也是几何对象研究的基本“套路”. 教师要注意梳理学生回顾的知识,帮助学生理清研究三角形的脉络:背景~三角形的概念~三角形边的关系,三角形中角的关系,三角形的角平分线、中线、高线概念及性质~三角形之间的相互关……. 借鉴于三角形的研究方法,平行四边形及其他几何对象的研究思路形成也就自然而然了.
问题2 的设计,学生经历从生活图片画出几何图形的过程,直观获得“哪些几何图形是平行四边形”的结论,自然形成平行四边形的概念(两组对边分别平行的四边形是平行四边形).
问题3 的设计,类比三角形的基本元素,自然获得平行四边形的基本元素有边、角、对角线等.学生类比三角形的研究方法,研究平行四边形的边、角、对角线关系,获取一些结论.
问题4 的设计,学生交流结论,相互评判,无论是证明还是举反例,目的是培养思维的严谨性,发展逻辑推理核心素养.
问题5 的设计,师生辨析,总结出平行四边形的性质定理:平行四边形对边相等;平行四边形对角相等;平行四边形对角线互相平分. 类比等腰三角形的性质定理与判定定理的关系,引导学生从性质定理的条件和结论来研究平行四边形的判定方法,符合学生的认知基础和认知规律.
问题6 的设计,与问题4 一样,培养思维的严谨性,发展逻辑推理核心素养.
上述问题串的设计自然而然,层层推进. 学生利用直观感知、类比等手段,掌握研究几何对象的基本“套路”,体会知识的产生发展自然而然.
4 创设自然而然的问题情境,推进数学性质探究
很多数学性质的获得,需要经历猜想、验证、归纳等探究过程. 探究过程必须是自然推进的,要立足学生的认知基础、遵循学生的认知规律、符合数学特点,要让学生明确“为什么有结论”和“有什么样结论”. 大多数的数学探究过程就是问题的解决过程,设计自然而然的问题情境,是探究过程自然、顺利推进的保证. 下面以沪科版八年级数学下册《一元二次方程的根与系数的关系》教学为例,阐述设计怎样的问题串,自然推进数学探究.
问题1请大家各自写出一个一元二次方程,并用求根公式求解.
问题2求根公式揭示了一元二次方程系数与根之间的关系,本质是通过一元二次方程系数的运算求出方程的根. 解下列方程并观察所得根与方程系数有何关系?用自己的语言叙述出来.
(1)x2-5x+6=0 (2)x2+2x-24=0
(3)x2+6x+8=0
问题3若一元二次方程ax2+bx+c=0(a≠1)有解,那么你在问题2 中所发现的关系对于它是否仍然成立?举例说明.
问题4若一元二次方程ax2+bx+c=0有两个实数根x1、x2,则该根与方程系数的关系是怎样的?并证明.
问题1 的设计意图是通过利用求根公式解一元二次方程,促使学生意识到一元二次方程的系数与根有关系,激发学生探究这种关系的欲望,解决“为什么有结论”的问题.
问题2 的设计是从特殊到一般,通过根的运算获得“若方程x2+px+q=0 有两实数根x1、x2,则x1+x2=-p,x1·x2=q”的结论,体现由简单到复杂,由具体到一般的研究思路,也是符合学生认知规律的.
问题3 的设计目的是让学生产生认知冲突,问题2 所获得的关系是有局限性的,对于二次项系数不为1 的一元二次方程不适用,很容易举例说明,新的问题也随之自然产生:二次项系数不为1 的一元二次方程,若有根,则根与方程各项系数有什么关系呢?学生的思维很自然地被引导到更一般的研究对象.
问题4 的设计目的是帮助学生获得一元二次方程的根与系数的关系,有了问题2、3 的结论,一元二次方程的根与系数的关系就水到渠成、自然而然,解决的是“有什么样结论?”的问题. 证明结论,目的是引导学生利用逻辑推理来说明结论的正确性,培养严谨的思维习惯,也更有利于对数学结论的理解和把握.
上述探究过程是在学生已有的认知基础上,对“一元二次方程”的性质进行探究,“为什么有关系”、“有什么样的关系”等问题都是学生在探究过程中自然发现并解决的,也是数学自然性的体现.
总之,数学是研究数量关系和空间形式的科学,它有着自身的发生发展规律,数学教学要遵循这个规律,设计出既符合数学学科发展的逻辑顺序,又符合学生心理发展特点的问题情境,发展学生学科核心素养,真正落实立德树人根本任务.
