一道解析几何高考题的调查与研究
2022-06-27福建省漳州市厦门大学附属实验中学邮编363123
福建省漳州市厦门大学附属实验中学 邱 云 (邮编:363123)
1 试题分析

命题分析本题以点的坐标满足的距离关系这一简单问题情境为载体,考查双曲线的定义、直线与双曲线的位置关系等主干知识.“线段长度乘积相等”蕴含了“四点共圆”的几何背景及交线的对称之美;动点T不改变两直线斜率之和的恒定性渗透了特殊与一般的数学思想.试题整体设计立足常规又超越常规,凸显了基础性、综合性的考查要求,有益检测数学运算、逻辑推理素养及观察猜想能力,体现了“价值引领、素养导向、能力为重、知识为基”新高考命题理念.



2 解题障碍
高考后学生普遍反映这题做得不理想.为了解学生的真实解题障碍,笔者设计了问卷对“物理类、历史类”各100 名考生做了第Ⅱ问解题情况调查.结果如下:44.5%的同学不知条件怎 么 用 放 弃 解 答.19.7%的同学知道先用特殊点猜得“斜率之和为0”.27.7%的同学因直线方程变量太多没有化简到方程①.23.4%的同学不知能化成式②,直接运用两点间距离公式,导致解题受阻.11%的同学算得式②,没能得到式③.8.8%的同学算得形式②,不知同理可得| |TB及式④.11.7%的同学求得最终结果.因新教材没学参数方程,没有学生用直线参数方程解题.
从调查情况看,学生普通存在三个问题. 一是对解析几何运算普遍存在畏难心理.将含有两个变量的直线方程代入曲线方程化简时,缺乏运算自信的同学占比较高,不敢尝试解题直接放弃的同学较多.二是知识理解与运用上存在思维定势.用惯了直线与圆锥曲线相交所得弦长公式于是固化思维,缺乏对弦长公式本质的理解.以为只有曲线的弦长才可用弦长公式,以致对| |TA这样的非弦长犯难,无奈只好用两点间距离公式计算线段长度,因运算繁琐,只能作罢.三是缺乏观图猜想意识.将点T置于特殊位置,根据图形的对称性,易发现所探求的两直线关于x轴对称.
3 推广引申
本题主要研究在点T运动变化下的不变性质.其核心条件是“|TA|·|TB|=|TP|·|TQ|”,满足此条件的圆锥曲线都具有“两直线斜率之和为0 的”特性.
推广1将“直线”改为“直线x=m”或“直线y=n”,其他条件不变,结论仍成立.证明类似“通法”.

推广4设点T(m,n)是不在抛物线C:y2=2px的一点,过T的两条直线分别交C于A,B两点和P,Q两点,且|TA|·|TB|=|TP|·|TQ|,则 直线AB的斜率与直线PQ的斜率之和为0. 证明类似“推广2”.
推广5已知⊙M与椭圆或双曲线或抛物线E:y2=2px交于四个不同的点A、B、P、Q,则过其中任意两点的直线的斜率与过另外两点的直线的斜率之和为0.如图1、图2,通过几何画板验证:kAB+kPQ=0,kAP+kBQ=0,kAQ+kBP=0.三组直线都具有对称性.
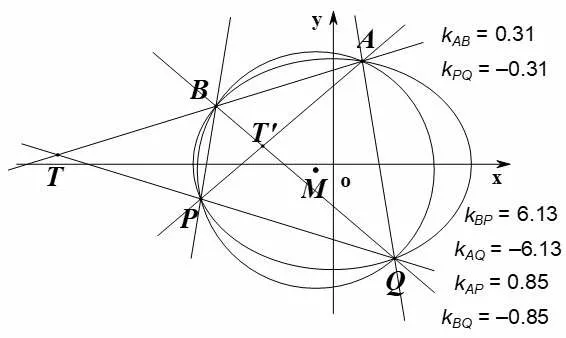
图1

图2
高 考 题 中 藏 在“|TA|·|TB|=|TP|·|TQ|”背后的的几何背景就是⊙M.因为圆锥曲线上的四点A,B,P,Q共圆,所以有|TA|·|TB|=|TP|·|TQ|,或|T′A|·|T′P|=|T′B|·|T′Q|.故“推广5”可转化为“推广2”证明.
4 反思感悟
近十年(2011-2020)高考全国卷解答题从未考双曲线综合题,今年高考在倒数第二题位置出现双曲线背景的解析几何大题,着实让师生感到意外.其实,2021 年“八省联考”已破例在第21题设置了双曲线大题,为新高考“去模式化”发出了信号.高考再现双曲线大题属情理之中.2017 年 浙 江 省 新 高 考 卷 第21 题 第2 问“求|AP|·|PQ|的最大值”就出现了线段乘积问题及弦长公式本质的运用,将非弦长|PQ|表示为是解题的关键.实行新高考综合改革后,没有了“考试大纲、考试说明”指挥棒,高考命题以“一核、四层、四翼”为基本遵循,突出素养导向,试题更加灵活多样,老师要加强对高考信息的研究,传统的“套路、模式与刷题”复习备考策略不再适应时代要求.
高三解析几何复习课,教师应立足“四基”做好运算示范,着力提升学生的运算素养,帮助学生“过好运算关”.一是先化简再代入.将直线方程代入曲线方程是求解析几何问题的常规步骤.这一步运算的准确性事关解题全局.通常先将直线方程化为y=kx+t或x=ky+t的形式,将圆锥曲线方程化为mx2+ny2=1 的形式,再将直线方程代入曲线方程运算更简洁.高考中很多同学直接将y-n=k1( )x-m代入x2-,陷入运算困境.二是活用同构运算.两条相关联的直线与圆锥曲线交汇生成的问题,往往具有算理相同的运算.只要认真算清一个表达式,同构替代可得另一表达式,从而简化运算.例如推广2 证 明用k2代换k1得到的 表达式;又如两条互相垂直的直线,用代替k.三是从特殊情况入手猜想结论.探求圆锥曲线定点定值问题,引导学生有意识取动点、动直线的特殊值,尝试猜出结论,揭示隐藏其中的一般性质.先求得运算结果有助优化运算方法、提升运算信心.例如本文研究的试题从点入手发现k1+k2=0.再如2020 高考北京卷第20题第2 问:求的值,令动直线l方程为y=0,得yp+yq=0,猜想于是将所求线段的比值转化为运算yP+yQ=0.运算猜想本质上是一种数学直觉.
另外,引导学生进行解题反思也是提升解析几何解题能力、发展运算素养的有效方法,例如思考结论是否能从特殊推广到一般.反思一道题“打开一片天”,从而开阔数学视野,积累更为丰富的运算经验.
