基于思维导图教学策略的复习课探究
2022-06-27杨松
杨松
摘要:《全等三角形》的专题复习课,它不仅仅是对知识的回忆、回顾,更是对错综复杂的知识进一步更全面、系统地梳理成体系,它承载着知识的巩固、联系、延展与再生。而思维导图在教学上,加强了各知识点之间的联系,对学生知识的整合、解题策略的优化、思维能力的形成与提高有着重要作用,能够有效突出重点,帮助学生突破难点。
关键词:全等三角形;复习课;思维导图
引言:
思维导图一般情况下会采用各种图形框架,图文并茂,实现对知识点的归纳、总结、分类,更依着知识的相关性进行延伸;体现着某个知识主体的来龙去脉的同时,也体现着贯穿知识脉络的研究方法、思想导向,把思维主体的整个过程清晰记录下来,并利用该种模式来对思维过程和形式全面掌握,对思维进行可视化处理;思维导图能还能及时发现自身在思维中存在的薄弱环节,及时弥补缺陷,更准确把握解题策略的条件切入点,优化解题方法。所以说,思维导图不但是知识脉络的载体,还是思维可视化处理工具,甚至是优化解题策略的指南针。思维导图在初中数学教学中也有着广泛的应用。
本文以人教版《义务教育教科书·数学》八年级上册(以下统称为“教材”)第十二章《全等三角形》专题复习课第二课时为例,交流分享在使用思维导图进行全等三角形复习的教学设计方面的几点探索和感悟,用以抛砖引玉。
一、以思维导图复习现旧知,达到复习巩固的作用
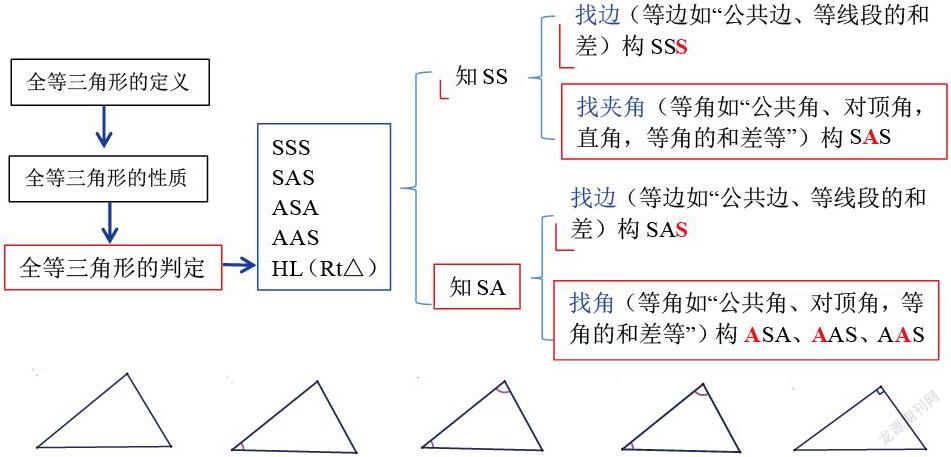
问题1:什么是全等三角形?性质是?判定?如何唯一确定一个三角形的形状?
师生元问题式问答复习,教师播放多媒体课件,知识以导图的形式逐步呈现.
[评析]以问答复习方式进行师生交流,运用思维导图式的知识梳理和呈现,不但可以达到节省时间高效复习旧知识,让学生对上节课所学内容快速回顾,做好本节复习课的基础准备;直观性的思维导图把全等三角形的定义、性质、判定方法和基本证明策略有机组合,让学生对全等三角形有了整体的视觉感受和认知,初步体会知识的内在联系,突出了全等三角形复习课中“梳理全等三角形的性质、判定等相关知识形成体系”的重点,也为突破“快速准确找到条件切入点,构造全等三角形解决边角关系的一般方法策略”的难点做基础准备。
二、以思维导图呈模型,知识延伸,串思维,找到解题策略
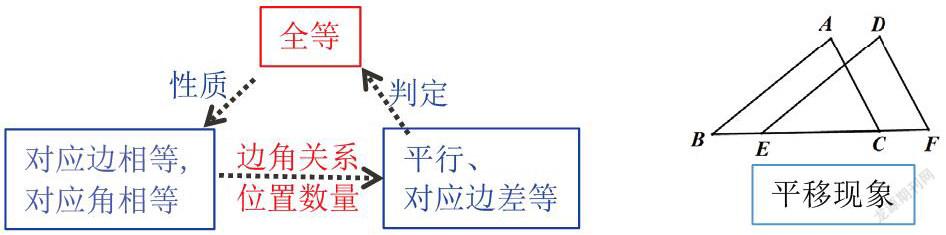
问题2:如图,已知B,C,E,F四点在同一直线上.
(1)若△ABC≌△DEF,AB与DE的数量关系是________,位置关系是_________;
(2)若AB平行且等于DE,BE=CF.求证:△ABC≌△DEF.
师:①审题,你的关注点是什么?
②根据全等的已知条件你联想到了什么?
③这两个三角形的边有何位置关系?可以通过什么变换得到?
生:全等;全等三角形的性质(对应边相等);平行;共线段,平移.
[评析]以思维导图进行平移现象分析,可以有助于学生看清出题者意图,高度概括题目意思,找到“三角形全等”与“边角的数量、位置”的关系,找到解题突破点,也更容易归纳出平移模型的一般解题策略。
问题3:已知△ABC≌△DBC,则∠ABC=_______,所以BC平分__________.
变式: 已知AB=AD,AF平分∠BAD,点O是AF上一点,延长BO交AD于点C,延长DO交AB于点E.
(1)求证: △ABO≌△ADO.还有其他全等三角形吗?请罗列出来.
(2)图中有哪几个三角形是等腰三角形.
师:①审题,你的关注点是什么?
②根据全等的已知条件你联想到了什么?
③这两个三角形有何特殊位置关系?可以通过什么变换得到?
生:全等;全等三角形的性质(对应角相等);角平分线;共顶点,共线段,翻折.
[评析]以思维导图分析翻折的全等现象,根据“全等三角形的对应边、对应角相等”的关系得到特殊的“边角的数量、位置”的关系,再高度概括提炼出全等三角形中隐含的“对称性”的关系,再由“对称性”联想到同样含有对称关系的“角平分线、垂直平分线、等腰”等知识;从而概括整理出“对称式的全等三角形模型”,找到解题突破点,也更为以后的解题归纳出一般解题策略,即“遇到含‘角平分线、垂直平分线、等腰’特征条件时,可以考虑添加辅助线补成全等三角形,再进行边角关系的证明”,为突破“为何、如何”添加辅助线的难点提供有效参考方法。
问题4:已知把△ABC绕着点A旋转得△AB’C’,∠BAB’=60°.求证:B’C’平分∠AB’C.
师:①审题时,你的关注点是什么?
②根据全等的已知条件你联想到了什么?
③这两个三角形有何特殊位置关系?可以通过什么变换得到?
④“特殊角60°”+“对应边相等”你又联想到了什么?
生:旋转,全等;全等三角形的性质(对应边、角相等);共顶点;等边三角形.
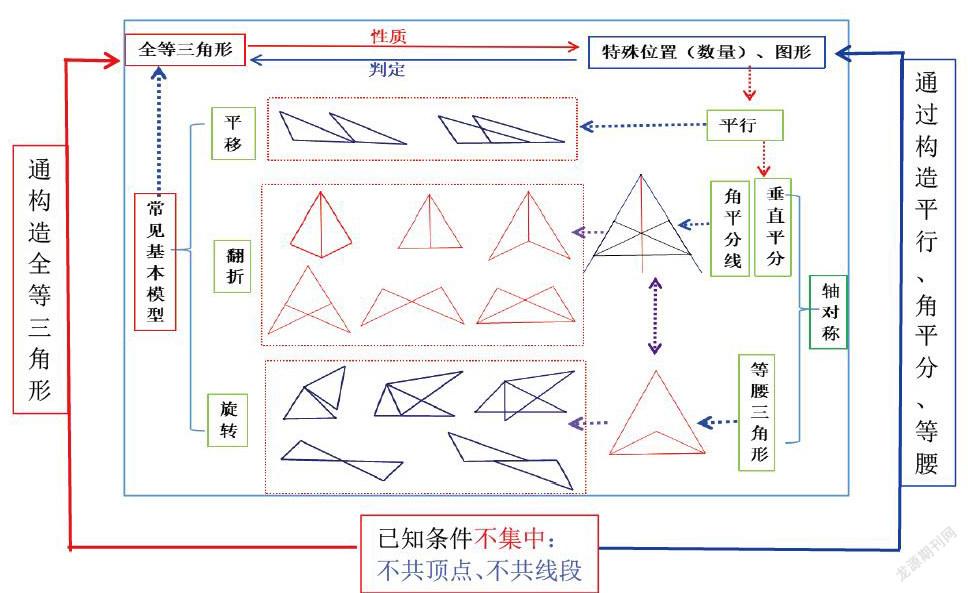
师生活动:师生共同逐题分析,用思维导图及时归纳总结平移、翻折、旋转下的全等模型,图象表征下牵引出的平行、角平分线、垂直平分线、等腰三角形等等相关图形,并不断强调不同的模型下它们的“共性”,即“全等三角形——对应边相等,对应角相等”的相同主线。逐步完善知识点,并拓展延伸出去,丰富主线知识。
三、参照思维导图学以致用,一题多解,优化策略
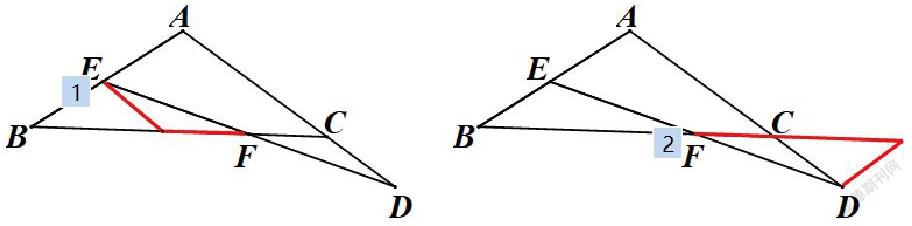
应用:如图点D是△ABC的边AC延长线上的一点,点E是AB上的点,BE=CD,DE与BC相交于点F,点F是DE的中点.求证:△ABC是等腰三角形.
师:①审题时,你的关注点是什么?是什么等量关系?
②根据已知条件你联想到了什么知识点?从图形你联想到什么全等模型的?
③缺什么条件?可以怎么补?为什么这样添加?
④你有多少种方法?能否归纳你的解题思路?哪一種方法最优?为何(因为哪些条件导致的)?
师生归纳解题思路:
[评析]通过习题再次体会从审题、从文字找特殊的边角关系(平行、角平分、垂直平分、等腰三角形……)、从图找相关模型(平移、翻折、旋转……),从已知和求证发现所缺;从所缺和相关模型找到补形的方向,从而确定辅助线的作法(把不共顶点、不共线段的量,通过辅助线集中在一起),构造所需的模型,再根据“全等三角形——对应边相等,对应角相等”实现全等三角形与边角特殊关系的转化。思维导图的呈现,让解题切入点有了对比,让解题思维可视化,能不重不漏实现多种思维方向,形成一题多解,这种可视化让不同的解题方法在同一版面得以直观对比,实现策略优化。思维导图让学生可以直观通过图象表征的“异同”和内在联系的“共性”综合对比归纳,形成一般方法策略。既突出了全等三角形的重点,也逐步分解难点,形成因内在关联而保持一致性的相同套路,也形成因已知条件的变化而如何选取切入点进行解题的最优策略。
当然培养学生如何画出高质量的思维导图?教师如何在课堂上恰当使用思维导图进行复习,使学生的学习效果达到事半功倍,而不是流于表面的形式累赘?这些都是值得我们思考和研究的。
参考文献:
[1]项佳 . 思维导图在初中科学课中的应用方法分析[J]. 亚太教育,2018,12(08):136-136.
[2]肖俊 . 思维导图在初中科学教学中的应用[J]. 南昌师 范学院学报,2019,24(06):27-31
[3] 李柏青. 复习课单元整体教学设计的实践与思考[J]. 数学通报,2013,52(3):31-36.
注:本文系南宁市教育科学“十三五”规划2019年度课题《基于思维导图教学策略的复习课探究——《全等三角形》复习课为例》(课题编号:2019C774)阶段性研究成果.
