数学问题意识培养应如何起步——基于一年级小学生的视角

于 勇

(江苏省苏州市吴江区思贤实验小学 215200)

《义务教育数学课程标准(2011年版)》明确指出：“创新意识的培养是现代数学教育的基本任务，应该从义务教育阶段做起，并贯穿于数学教育的始终.学生自己发现和提出问题是创新的基础；独立思考、学会思考是创新的核心.”一年级作为义务教育阶段的起始年级，应在教学实践中扎实培养学生敢问、会问、善问的问题意识，以此引领他们慢慢学会从数学的视角发现问题、提出问题，创造性地分析和解决问题，逐步提升他们数学学习的自主建构及知识“理解”证据的呈现能力.

1 基于教学对话，切实厘清什么是数学问题

可以想见，一个连数学问题是什么都不知道、不明晰的学生，不可能提出富含较高思考价值与认识深度的数学问题，引领他们认识并真正厘清什么是数学问题，才是开启对他们数学问题意识培养的逻辑起点.一年级起步很难开展讨论合作、动手操作等自主探究活动，而借助师生对话组织教学，可以有效将学生认知与思维等探究活动不断推向纵深，故而被教师广泛使用.教师可在高频率师生对话中，通过适当形式引导学生弄清什么是数学问题，为促使他们提出真正意义上的数学问题迈实第一步.

如在“比长短”教学过程中，教师提出这样的问题：“下面三根绳子中，哪一根最长呢？请在它后面括号内画√.”学生能够很快找到最长的一根，并在其后面括号内画上“√”.“大家为什么会选择这一根呢？”教师接着追问.“是老师让我们选择最长的绳子，并在它后面画对号的.”“是的，我刚才提出哪一根绳子最长的问题,需要大家做出选择，这就是一个数学问题.”教师继续追问：“同学们，你们也能像老师一样再提出一个数学问题吗？”由于教师刚才提出的是“哪一根绳子最长”的问题，学生自然就能提出“哪一根绳子最短”的对比性数学问题.

又如在学习“9的分与合”时，教师利用课件把9根小棒分成两堆.“请同学们仔细观察，左边一堆有几根小棒？”“这需要你们先数一数，然后再用数字来回答的问题就是一个数学问题.”学生回答后，教师继续与学生对话，哪位同学也能提出一个用数字回答的问题，学生自然也能准确、快速地提出“右边一堆有几根小棒”的数学问题.

在师生对话过程中，教师先是示范性提出一个数学问题，需要学生做出选择或用数字来回答，然后明确告诉他们这就是数学问题，最后引导学生结合师生对话的具体情境，参考教师提出的范例问题，提出对比性数学问题.随着持续、深入的师生对话，学生就会慢慢明白需要他们做出选择、回答或解释等相应认知活动的问题就是数学问题.只有如此，才会使学生有机会独立思考、互动交流、发现问题，进而使学生提出问题成为可能.

2 强化数学表达，深度感知数学问题结构

一个真正的数学问题一般是由两个条件和一个问题构成的，学生对这一逻辑结构的认识是提出问题、培养问题意识的认知基础.在具体认知活动中，要强化学生数学信息“三句话”的表达训练，以此引导他们深度感知数学问题的基本结构，深度理解前两句是构成一个问题的条件，第三句是由数学问题转化而成的运算结果.

2.1 在数字认识中，模仿学说三句话

在认识10以内的数字后，绝大多数学生能用学过的数字比较熟练、准确地说出一句话.要让学生快速、有序地说出三句话恐怕是不现实的，可他们善于模仿及图形认知，可以此作为训练他们学说数学信息三句话的切入点.如在学生认识“>”、“<”或“=”之后，就可以根据教学需要，有意识地引导学生学说数学信息三句话.

△ △ △ △ △ △

□ □ □ □ □ □ □ □

如上，先是引导学生数一数△与□各有几个，并填写下来，然后去比较□比△多几个，让他们完成这样的练习：△有( )个，□有( )个，□比△多( )个.当学生找到正确答案后，也就形成了数学信息三句话，△有6个，□有8个，□比△多2个.这时，教师可以带领学生共同读一读，然后放手学生照着样子自己读一读，同时教师进一步追问：△有( )个，□有( )个，△比□少( )个.最后，在正方形下方添加4个○，让□、△分别与○形成结构性数学信息，让学生再去说一说.当然也可用同一类图形创设数字认识情境，对学生进行“共有多少个图形”的数学信息三句话训练.

一年级上学期数字认识资源是异常丰富的，教师在将教学活动指向数字认识的同时，要灵活、规范、有序地引领学生参与模仿学说数学三句话的基本训练，以此引领学生初步建构数学问题结构的基本表象.

2.2 在情境理解中，有序学说三句话

数学信息三句话一般分别包含一个数字，三个数字间的正确逻辑关系构成了数学问题的启蒙样态，并不是任意包含数字的信息就可以构成一个数学问题.一年级上学期教学内容多以情境图、图文结合、简单符号等形式予以呈现的，蕴含丰富的数学信息及逻辑关系.教学不仅要引导学生关注情境中的相关数学信息，更要关注数据间的逻辑顺序，引导他们有序说出数学信息三句话，如此才有可能引领学生真正认识数学问题的基本结构.

如“得数在5以内的加法”(图1)，主要是引导学生从“合起来”的角度明晰3+2=5的基本算法，关键是找到“原来有3人浇花”“又有2人来浇花”等相关数学信息.可实际上最先让学生得到的数学信息是“一共有5人在浇花”，进一步观察后才能发现“原来有3人在浇花”“又有2人来浇花”，学生难以搞清三条信息间的逻辑关系.解决这一问题的有效途径是先让学生充分说出情境中的基本信息，然后引导他们思考应该先说什么，再说什么，最后说什么.在此基础上，教师出示：原先有( )人在浇花，又来了( )人来浇花，现在一共有( )人浇花.学生在情境理解过程中，规范有序地说出了数学信息三句话，由此基本明确了数学加法问题的基本结构.

图1 图2

2.3 在符号理解中，完整学说三句话

“用括线和？表示的实际问题”是苏教版数学教材第一次出现的相对完整的数学问题，主要是引领学生初步了解括线和“？”表示的实际意义，会从括线和“？”表示的实际问题中收集信息，说清已知什么，要求什么，进而让学生认识理解真正意义上的数学问题.如图2情境就包含括线和“？”两个数学符号，正确理解弄清每个符号的基本内涵是解决这个问题的关键.教师首先引导学生提取情境中的数学信息，出示“盘子里有5个苹果”与“盘子外有3个苹果”，并明确告知学生这些数字就是已知条件；然后结合相应的演示动作告诉学生括线表示把盘子里和盘子外的苹果合起来，括线下面的“？”表示把盘子里和盘子外的苹果合起来一共有多少个？同时明确告诉学生这就是数学问题，接着引导学生完整地说一说这三句话，教师再次明确地告诉学生这就是一个完整的数学问题，它包含了两个已知条件和一个需要回答与解决的问题.

教材中具有丰富的由括线和“？”构成的情境素材，教师应不失时机地引导学生经历提取信息、找到问题、正确解答的基本过程，并于过程中引导学生想一想、说一说具体条件及问题，逐步在他们大脑中建立起丰富的数学问题结构表象.

3 训练提问技能，打好问题意识培养基础

3.1 借助解释算式含义，引导学生提出问题

教材中有关解决问题的教学内容，基本都是通过图画、简单符号、图文结合的形式予以呈现的，主要是引导学生在提取信息、弄清图意的基础上，通过一图一式、一图两式、一图四式等逐步深入的方式对问题予以解决.为此，可引导学生在解释算式具体含义的过程中，经由从答案到问题的形式催生出完整的数学问题.如一图四式的练习(见图3)，在学生列出正确算式后(以第一个算式为例)，教师可以引导他们思考6、2、6+2分别表示什么意思？根据学生回答依次出示：地上有6个红萝卜，小白兔的筐子里有2个红萝卜，一共有多少个红萝卜？这样一个真正意义上的数学问题就在学生解释算式含义的过程中油然而生.

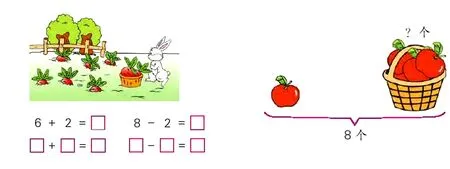
图3 图4

3.2 借助巧妙变式练习，引导学生提出问题

变式是指通过变换同类事物非本质特征的表现形式，变更观察事物的角度和方法，从而突出事物的本质特征，突出那些隐蔽的本质要素，让学生在变式中思维.在学生知道一个真正数学问题的基本结构后，教师可以通过巧妙变化条件的方式衍生出数学问题.如这样的练习(见图4)，就可引导学生在提取信息、提出问题的基础上，通过变换多种水果图片、相应的数量及“？”的位置，引领学生提出更多的变式问题，让他们真正意识到由于实物、数量等条件的不断变化，提出的数学问题自然也会有所不同，但“已知整体，求部分”减法的实质与数学模型始终是没有变化的.