浅议辅助线在初中平面几何解题中的应用

李士伟

(山东省济南市平阴县玫瑰学校 250407)

添加辅助线对学生的能力要求较高，为更好的提高学生的解题自信，既要注重为学生讲解添加辅助线的相关理论知识，又要优选经典例题为学生展示辅助线的应用过程，启发学生高效解题，以免其在以后的解题中走弯路.

1 结合对称点添加辅助线

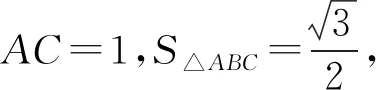
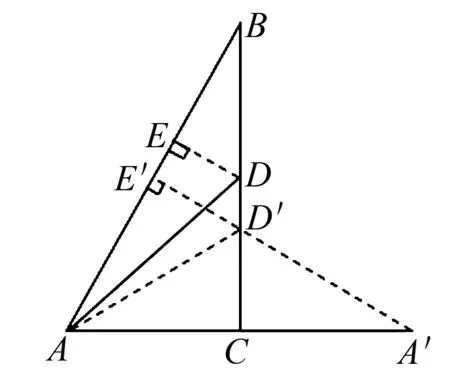
图1

再如图2，在△ABC中，AB=2，BC=3，D是三角形内的一点，CD=2，∠ADC+∠B=180°，求解当∠B为何值时，△ABC和△ADC的面积差最大，最大值是多少？

图2

解析将△ADC沿着AC进行翻折得到△AD′此时两个三角形全等，∠AD′C+∠B=∠ADC+∠B=180°，因此，四边形ABCD′内接于圆，所以AB=CD=CD′=2,得出四边形ABCD′是等腰梯形，所以A′D′∥BC.

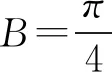
点评解答平面几何线段长度最小值问题时可借鉴“将军饮马”模型的思想方法，通过找到对称点添加辅助线确定最小值点的具体位置，问题也就迎刃而解.

2 结合图形性质添加辅助线

如图3，等腰△ABC的内切圆O分别和三边切于点D、E、F，若AB=AC=5，BC=6，则DE的长为( ).

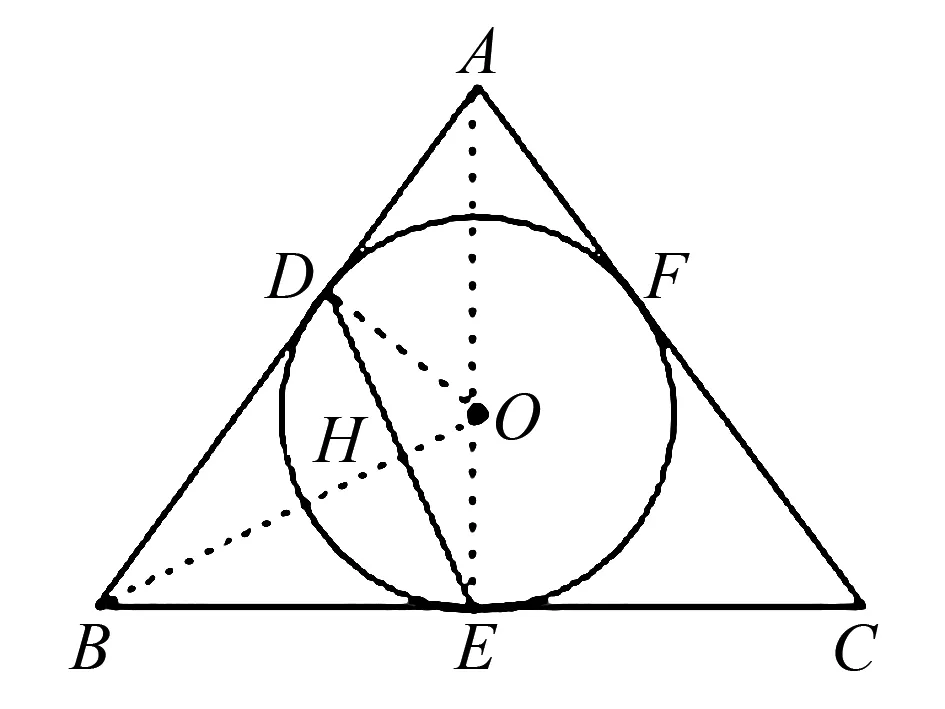
图3

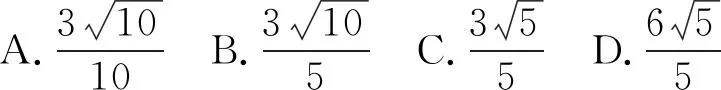
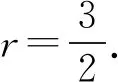
再比如，如图4所示，在梯形ABCD中，AD∥BC，对角线AC和BD垂直，且相交于点O，MN是梯形ABCD的中位线，∠DBC=30°.求证：AC=MN.

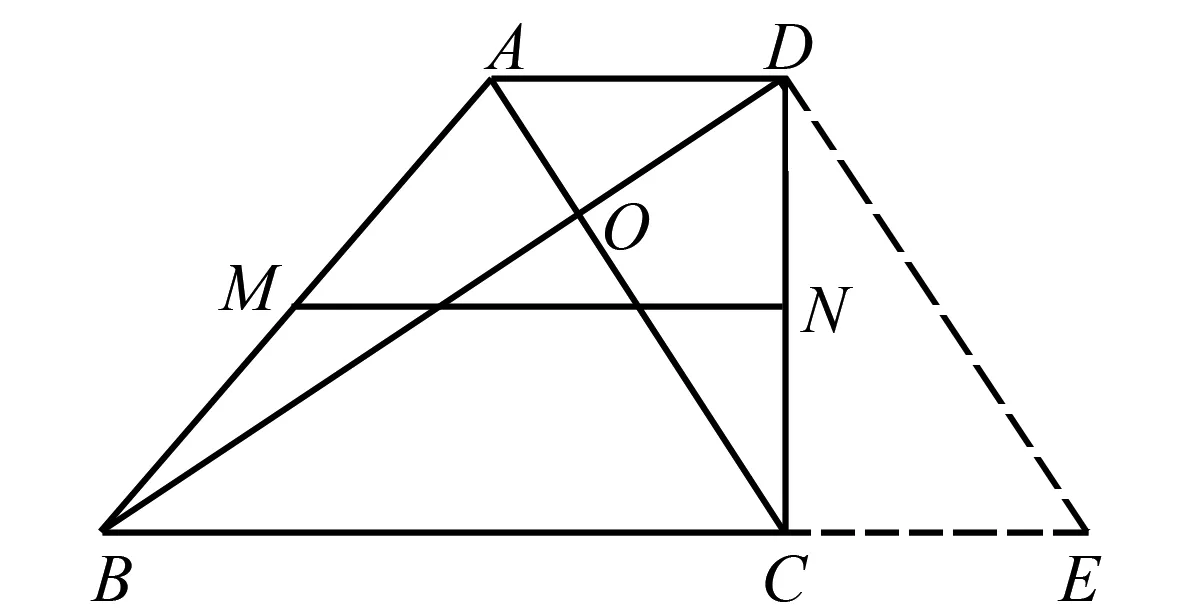
图4

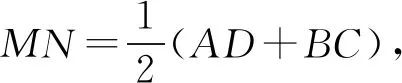
点评运用辅助线分析平面几何问题时应结合问题题设的情境，认真分析相关图形的性质，如矩形、平四边形、菱形、圆形等，结合图形性质添加辅助线.通过添加辅助线运用图形性质进行求解.

3 结合线段关系添加辅助线

如图5，已知AP∥BC，点E是DC的中点，且AD+BC=AB，求证：AE⊥BE.

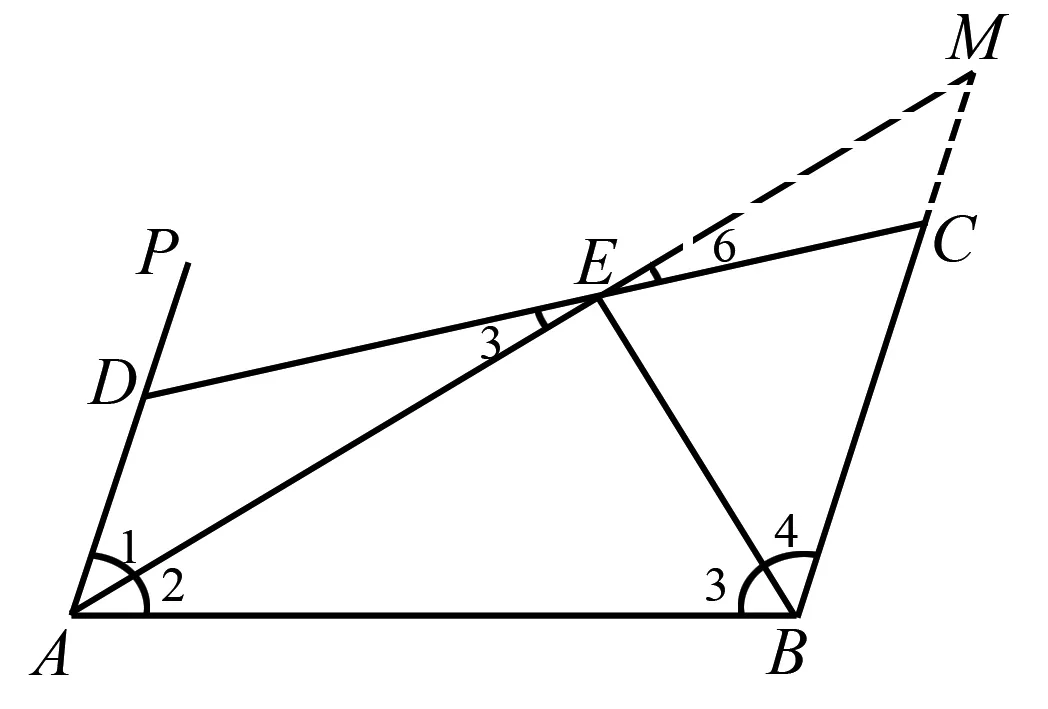
图5

根据题意，分别延长AE，BC交于点E.因为AP∥BC，所以∠1=∠M.又因为E是DC的中点，所以DE=EC，而∠5=∠6，所以△ADE≌△MCE，则AD=MC，AE=EM，又因为AD+BC=AB，所以MC+BC=AB，而MC+BC=BM，所以AB=BM，所以△AEB≌△MEB，所以∠AEB=∠MEB，又因为∠AEB+∠MEB=180°，所以∠AEB=90°，即，AE⊥BE，得证.

再比如，如图6所示，四边形ABCD是任意四边形，E、F、G、H是AB、BC、CD、DA的中点，M、N是对角线BD、AC的中点，求证：EG、HF通过MN的中点.

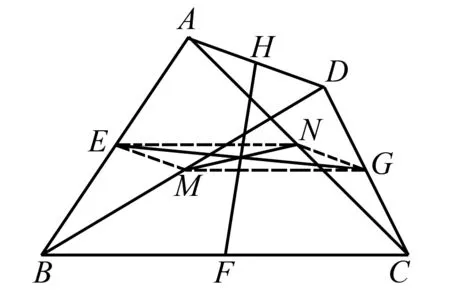
图6

解析欲证明三条线段在图中的关系，需要找出其存在的内在关联，题目已知条件中的中点比较多，可以任意选择一个顶点，如A作为位似中心，根据位似比将BC缩小，连接EN，得到EN等于和平行BC的一半，采用相同的方式组成更易于解答问题的平行四边形，从而完成题目的解答.

点评当习题的已知条件中涉及到线段的长度关系时，添加辅助线时应注重等量代换，而后运用三角形全等、相似等相关知识进行破题.

4 结合角度关系添加辅助线

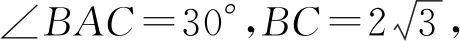
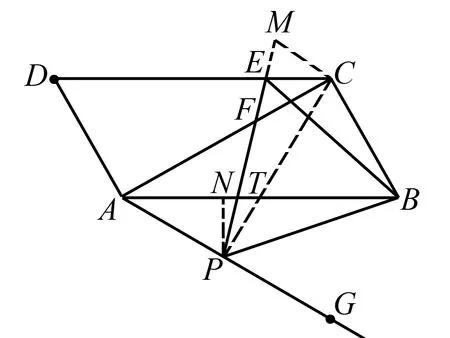
图7

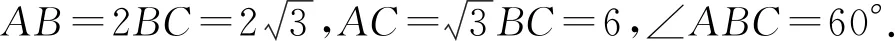
综上，为更好的提高学生应用辅助线解答初中数学平面几何的能力，教师在讲解例题的过程中既要注重与学生积极互动，驱使学生主动的思考、讨论，又要结合具体例题进行辅助线应用的方法点拨，使学生积累更多的添加辅助线的经验.另外，还应鼓励学生做好听课以及平时训练的总结，掌握不同题型添加辅助线的技巧.