电容驱动型多级感应线圈炮模型简化
2022-06-23郭灯华史铎林关晓存管少华吴彪
郭灯华, 史铎林, 关晓存, 管少华, 吴彪
(海军工程大学 舰船综合电力技术国防科技重点实验室,湖北 武汉 430033)
0 引 言
电磁发射装置将电能转化为机械动能,利用电磁力推动弹丸加速[1],提高了炮弹的出口速度,在新型武器系统研究中拥有重要地位。电磁炮按照结构不同分为轨道炮、线圈炮、重接炮[2-3],其中感应线圈炮结构简单、设计灵活[4],通过驱动线圈与电枢之间的电磁力实现炮弹加速,发射过程中电枢与驱动线圈之间无物理接触,且可控性强,不仅在武器系统中有广泛应用,还在航天、航空领域拥有广阔的发展前景[5-8]。
精确的感应线圈炮的控制模型十分重要,虽然感应线圈炮的结构简单,但是发射过程中的线圈与电枢的耦合使得线圈炮的数学模型复杂。在国内外线圈炮的研究中,都是通过不断地精确其模型来提升其发射效果。早在20世纪90年代,Sandia国家实验室开发的WRAP-10[9]、SLINGSHOT[10]以及CEM大学的Axi-coil[11-12]程序建立了同步线圈炮的动态模型仿真以检验发射器的性能。除此之外,针对动态过程中各种可能影响发射性能的因素,也有诸多相关模型仿真研究。文献[13]考虑线圈发射装置中电枢结构受径向磁场力的影响,建立了完整的磁流体力学模型,并以此计算出最优的电枢结构,实现了在高能量下使电枢形变最小。文献[14]针对电枢捕获效应的数学模型做定量分析,在模型中通过改变驱动线圈参数来减小电枢的捕获效应,使发射效果最优。文献[15]通过在驱动线圈中放置检测装置来评估线圈强度,通过测试与评估改进驱动线圈的结构。文献[16]设计了一种非对称的驱动线圈模型,为每一级线圈单独设计结构以获取更好的结果。
由于趋肤效应的影响,感应电流在电枢中的分布是不均匀的,电流丝法将电枢分为若干电流环,当细分足够小时可以假设每个环上的电流是均匀的,以此来精确细化模型[17]。运动过程中,电枢受到的电磁力与电枢和驱动线圈间的互感梯度成正比,在建立的模型中,互感梯度需要得知运动中不同位置各电流环与驱动线圈的互感[18],可以通过有限元软件的静态模型中计算,也可以通过互感计算手册来查表计算[19]。相关研究对基于电流丝法建立模型已经有了比较成熟的方法,但是对于过程中未触发的驱动线圈,必然会受到之前触发线圈的影响[20]。回路中功率开关器件的存在使放电过程非线性化。触发与未触发的驱动线圈要做分开处理,不仅增加了模型复杂程度,而且计算时容易出现错误,模型要求高。
本文将基于电流丝法建立动态过程的完整模型,用开关函数以及虚拟大电阻等效驱动线圈回路晶闸管以及二极管的工作状态,整合已触发和未触发的驱动线圈模型,简化电路的数学模型。研究线圈的最佳触发策略,并利用MATLAB/Simulink建立线圈炮的路模型,电流丝与驱动线圈互感通过Ansys有限元仿真软件计算获得,将结果导入到Simulink模型中,减少路模型实时计算工作量,提升仿真速度,将结果与有限元仿真结果进行比较,并在实验平台进行实验,验证模型的正确性。
1 电流丝法原理
1.1 线圈炮模型
为了简化线圈炮的分析,作如下假设:
1)线圈是理想圆且所有线圈同轴;
2)电枢是理想圆柱筒,各处电导率和密度相同;
3)电枢位于线圈中心位置,且与线圈同轴;
4)忽略线圈外部弱导磁材料的影响。
基于线圈炮的轴对称性,采用电流丝(current filament method,CFM)以电阻、自感、互感、电感梯度、电压等位参数,将三维问题简化为二维问题,建立线圈炮的电磁路方程。
电流丝法模型如图1所示,由于电枢电流沿轴向分布,若将电枢划分为m个同心圆环,则当圆环截面足够小时,可以认为感应电流在截面上均匀分布,即用m个“电流丝”来等效电枢感应电流。这样,线圈炮路方程可以表示为变系数常微分方程。
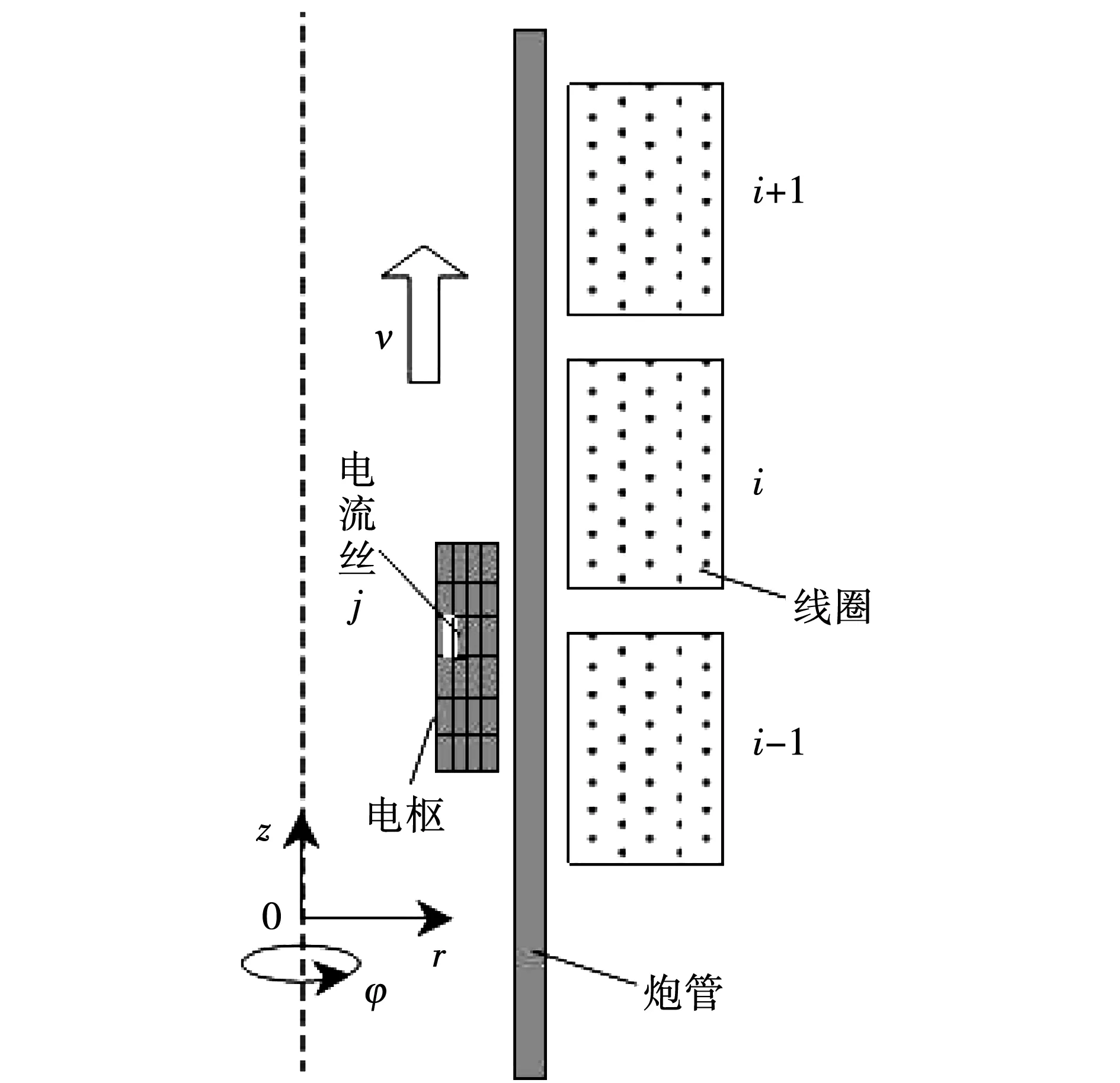
图1 线圈炮电流丝法示意图
线圈通常采用litz线绕成多匝结构,匝间彼此绝缘,可以忽略线圈导线涡流,因此,单个线圈中每匝激励电流相等。假设激励线圈有n级,根据基尔霍夫电压定律,可以将电压方程用矩阵形式表示为:
(1)
式中:Us表示线圈断开电压,是n维向量;φs表示线圈磁链,是n维向量;Rs表示线圈电阻,是n×n矩阵;Is是线圈电流,n维向量;φr是电枢环磁链,m维向量;Rr是电枢环电阻,m×m矩阵;Ir是电枢环电流,m维向量。
磁链方程为:
(2)
式中:Ls是线圈电感矩阵,n×n矩阵;M是线圈和电枢环互感矩阵,n×m矩阵;Lr是线圈电感矩阵,m×m矩阵。
电枢受到的电磁推力方程为
(3)
式中dM/dz表示沿电枢发射方向——轴向的互感梯度矩阵,是n×m维矩阵。
运动方程为:
(4)
式中:m是发射体质量;v是电枢速度;z是电枢位置。
1.2 电容驱动型电流丝法
电容通过高功率充电机恒流充电模式[21],连接晶闸管、二极管以及负载组成脉冲形成网络[22]。电容驱动型线圈炮电路如图2所示,当晶闸管触发时,电容向线圈释放电压,当电容电压释放至0,线圈电流再通过二极管支路续流,二极管支路串联电阻可以减小续流时间,降低晶闸管和二极管损耗。
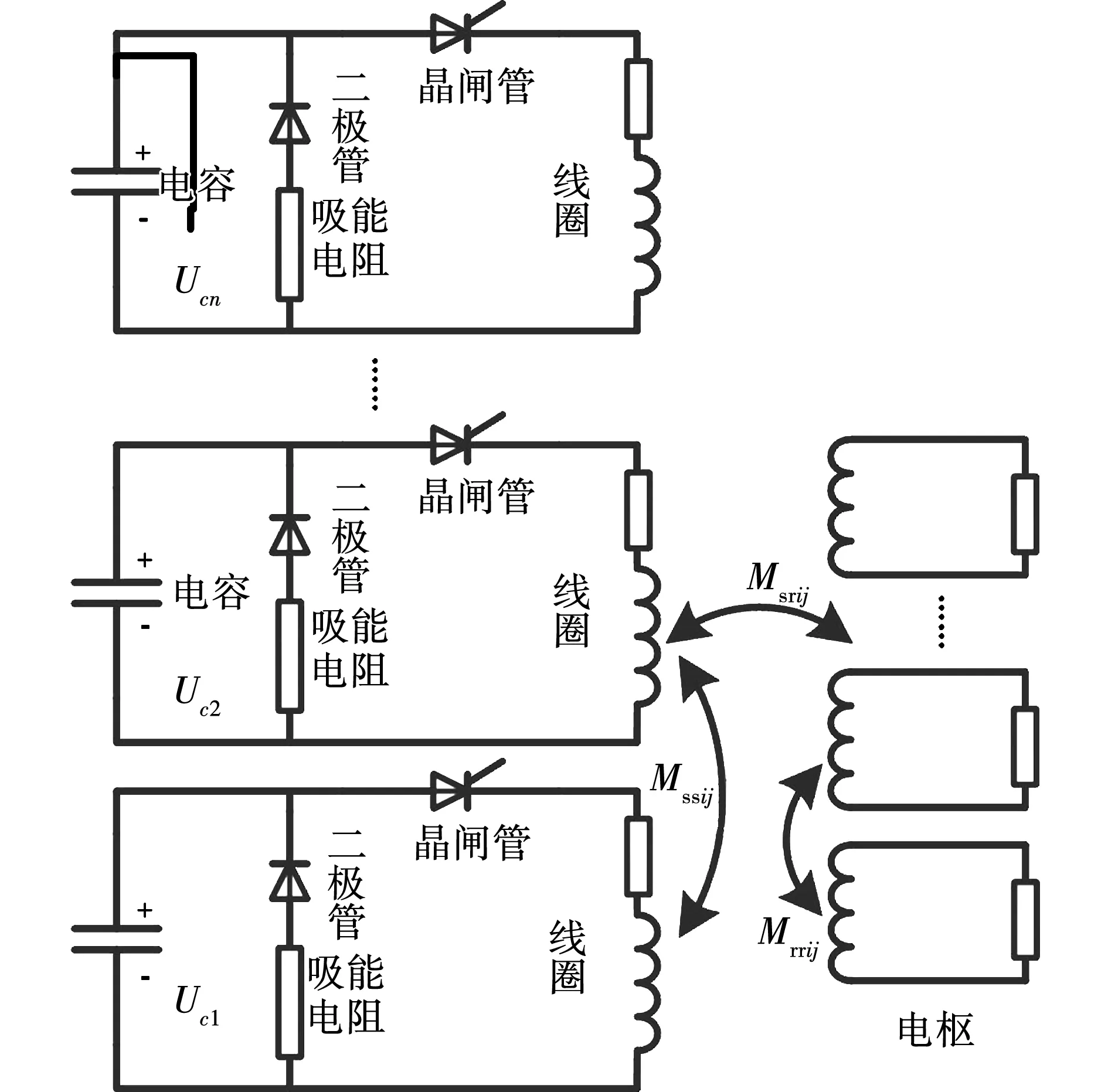
图2 电容驱动型线圈炮电路图
由于晶闸管和二极管的存在,造成供电回路的非线性,使得电流丝法建立的线圈回路方程复杂,分晶闸管触发前和触发后两种情况。
根据式(1)和式(2),晶闸管触发前第i级线圈的回路方程为:
(5)
式中:usi和isi是第i级线圈电压和电流;Mi1,Mi2,…,Mim是互感矩阵第i行。
晶闸管触发后,第i级线圈的回路方程为
(6)
式中rs是线圈电阻。
电枢电流方程为
(7)
晶闸管触发后,电容放电分两个阶段,第一阶段通过电容向线圈放电,如图3所示。
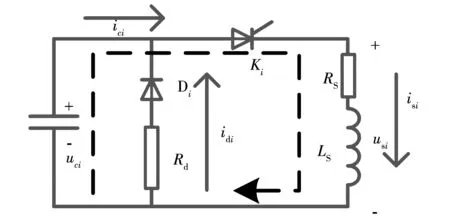
图3 电容放电电路图
电容放电回路方程为:
(8)
式中:C是电容值;uci和ici是第i级电容电压和电流;idi是二极管支路电流。
当电容电压降为0后,电容放电转入第二阶段二级管续流阶段,如图4所示。
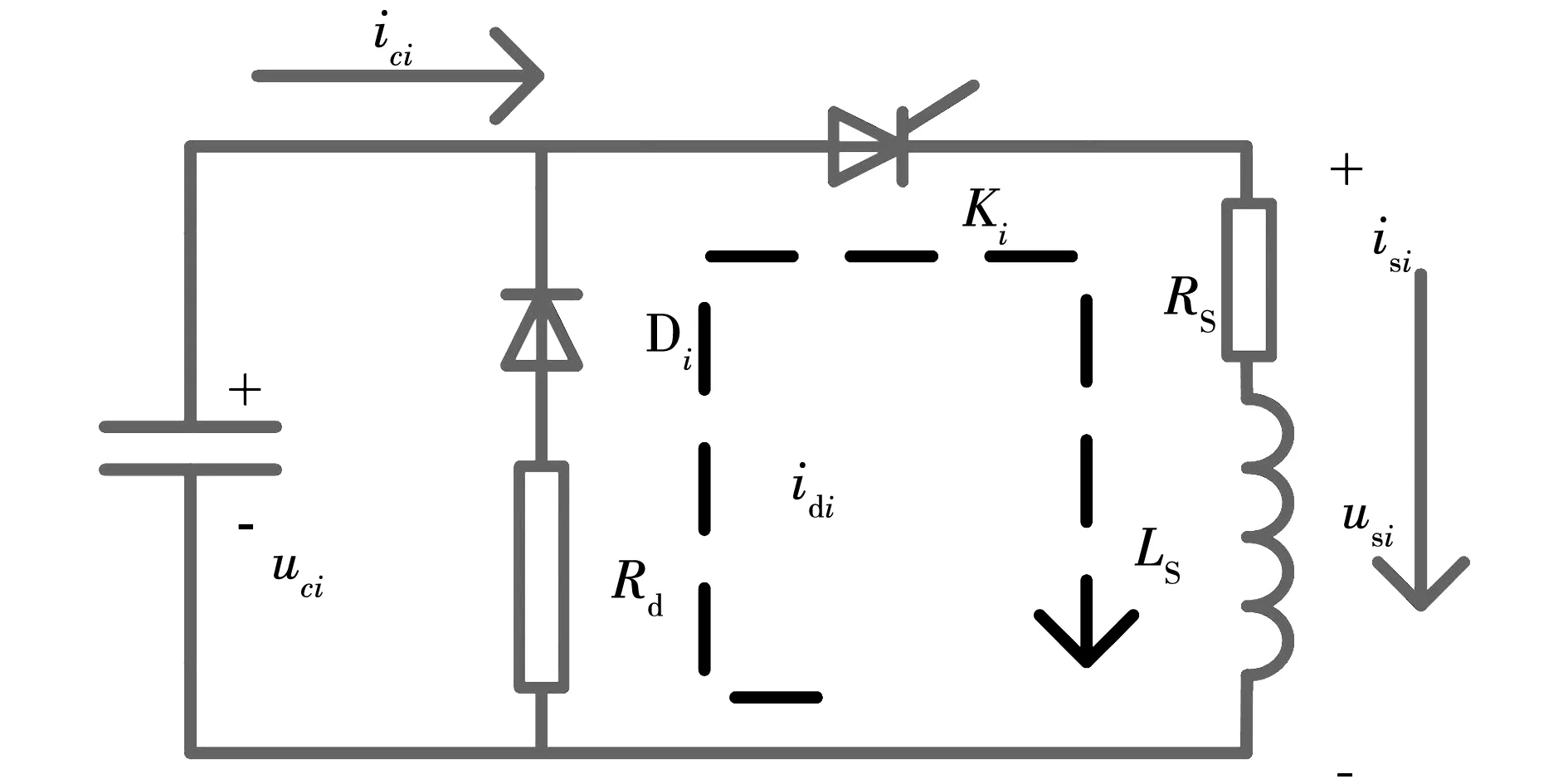
图4 二极管续流电路图
续流回路方程为:
(9)
式中rd是二极管支路电阻。
一般来说,多级线圈炮是按顺序逐级触发供电的,设第1~k级线圈已触发供电,第k+1~n级线圈未供电,汇总前面的分析,此时线圈炮回路方程用矩阵形式表示为:
(10)
(11)
式中:v是电枢运动速度;下标1_k表示向量或矩阵取对应元素1,2,3,…,k;下标k+1_n表示向量或矩阵取对应元素k+1,k+2,…,n,例如Mk+1_n是(n-k)×m矩阵,形式为
2 改进型电流丝法
2.1 等效电阻法
原有电流丝法应用在电容驱动型线圈炮时,由于半控器件引入非线性,增加了分析困难。由式(9)所描述的回路方程可知,需要根据触发情况,对n级线圈进行分段处理,已触发的k级线圈和未触发的n-k级线圈要采用不同的微分方程组。
为了解决这种情况,在线圈回路引入虚拟大电阻,如图5所示。若晶闸管未触发,则线圈支路串入大电阻;触发后,大电阻变为0。
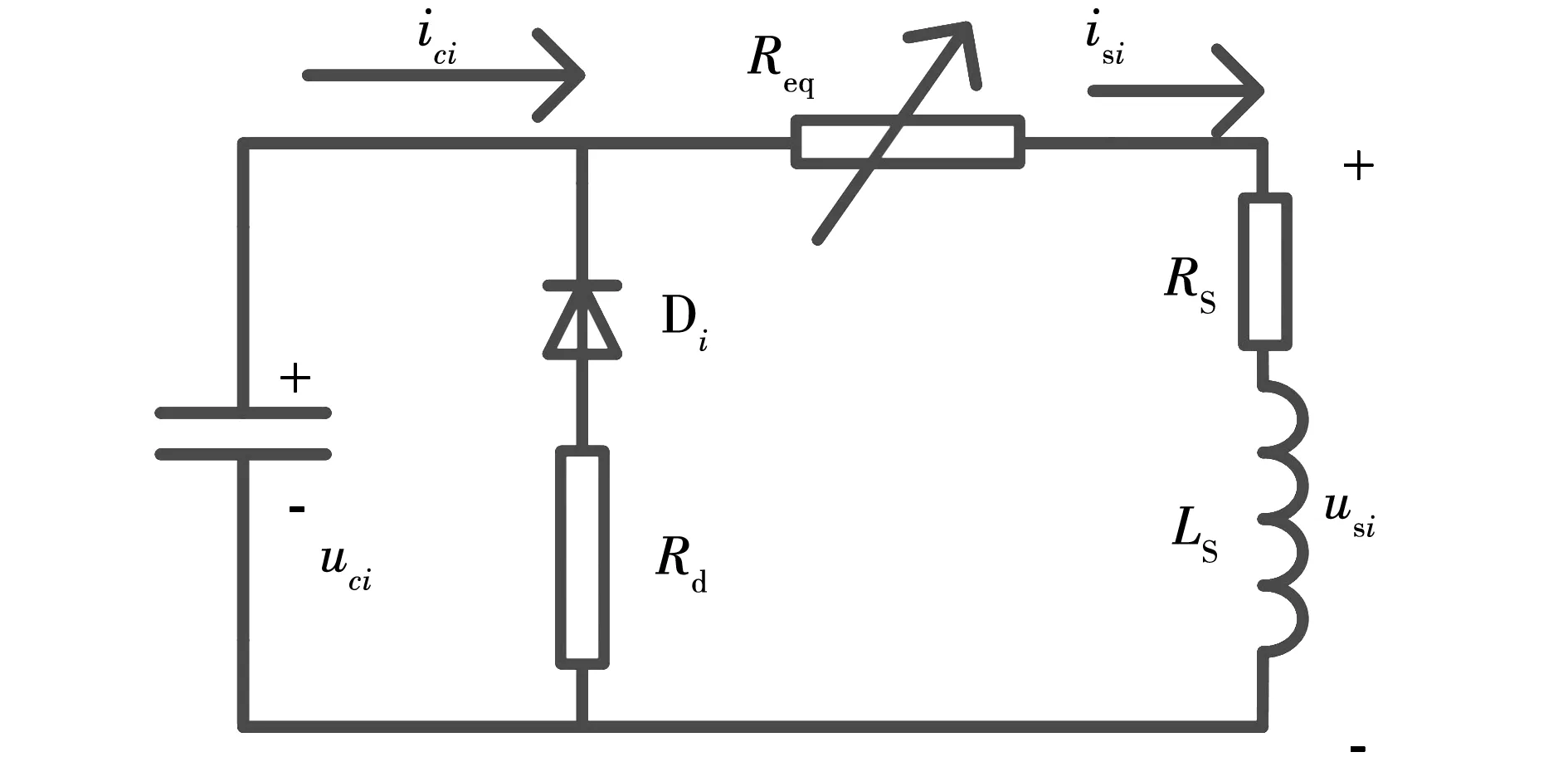
图5 等效电阻放电电路
加入虚拟大电阻后,式(10)可以写为
(12)
式中Req1_k是k×k对角矩阵,元素是req。当req足够大时,Is近似相等为0,式(12)和式(11)具有相同形式,因此,将触发与未触发状态线圈回路方程整合列写为
(reqS+Rs)Is。
(13)
式中:req是虚拟大电阻,根据正常工况,电容储存电压值为6 000 V,若要使虚拟大电阻等效关断时的晶闸管,需要考虑使其留过电流与该工况下的漏电流近似相等,已知晶闸管的漏电流一般小于10 mA,那么根据计算,虚拟大电阻的阻值可以是1 MΩ;S是开关对角矩阵,S=diag[0,0,…,0,1,1,…,1],前k个对角元素是0,后n-k个对角元素是1,表示前k级线圈触发,而后n-k级线圈未触发。这样,结合电枢方程,整个线圈炮改进电流丝法回路方程可以写为
(14)
引入虚拟大电阻后,线圈炮路方程不必采用分段微分方程组形式,可采用统一形式,大大简化分析计算。
相应地,电容放电回路也可以处理更简单,不需要考虑本级是否触发导通,直接采用式(8)和式(9)计算电容电压,当回路存在大电阻时,计算出的放电电流近似为0,可以等效认为本级未触发。
2.2 系数分析
分析式(13),由于各线圈之间相对位置不变,电枢电流丝之间相对位置也不变,因此,Ls、Lr是定常矩阵,Rs、Rr也是定常矩阵。而M、dM/dz是变系数矩阵,是线圈和电枢之间相对距离的函数,电流丝与线圈的互感关系如图6所示。
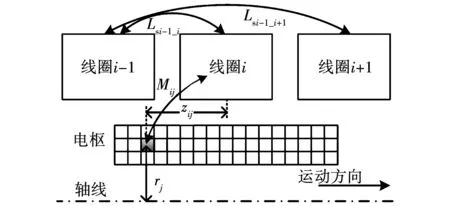
图6 电流丝自感互感矩阵示意图
由于M、dM/dz矩阵是随电枢位置z变化的系数,使得式(14)是变系数微分方程,对其求解比较费时。对式(14)进行变换,令:
传统农业植保工作的开展,以大型机械、人工操作为主导,前者具有作业效率高的特点,但却存在设备成本高的缺陷;后者呈现耗时长、人力资源多的问题[2]。而在无人机技术的衍生下,植保无人机的使用改变了传统植保模式,使植保工作更具快速性、高效性。植保无人机的优点具体如下。
(15)
则式(13)可以写为
(16)
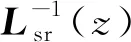
2.3 触发控制
电容驱动的线圈在晶闸管触发后,由于线圈时间常数较大,电流上升存在一定时间,当电枢速度较高时,上升时间内电枢会运动较长距离,而线圈和电枢耦合出力范围较短,因此,需要考虑电流上升时间和电枢运动速度。
该触发方式是在电枢运动至耦合出力点较大位置前,提前触发线圈,当线圈电流达到最大时,电枢恰好运动到耦合出力点,使电枢推力达到最大。
触发方式示意图如图7所示,触发时刻电枢位置是z,第i级线圈和电枢最佳耦合位置是Zsi,电枢速度是v,线圈电流上升时间是Tr。则第i级线圈触发在满足下式关系时,可获得较优触发效果,有
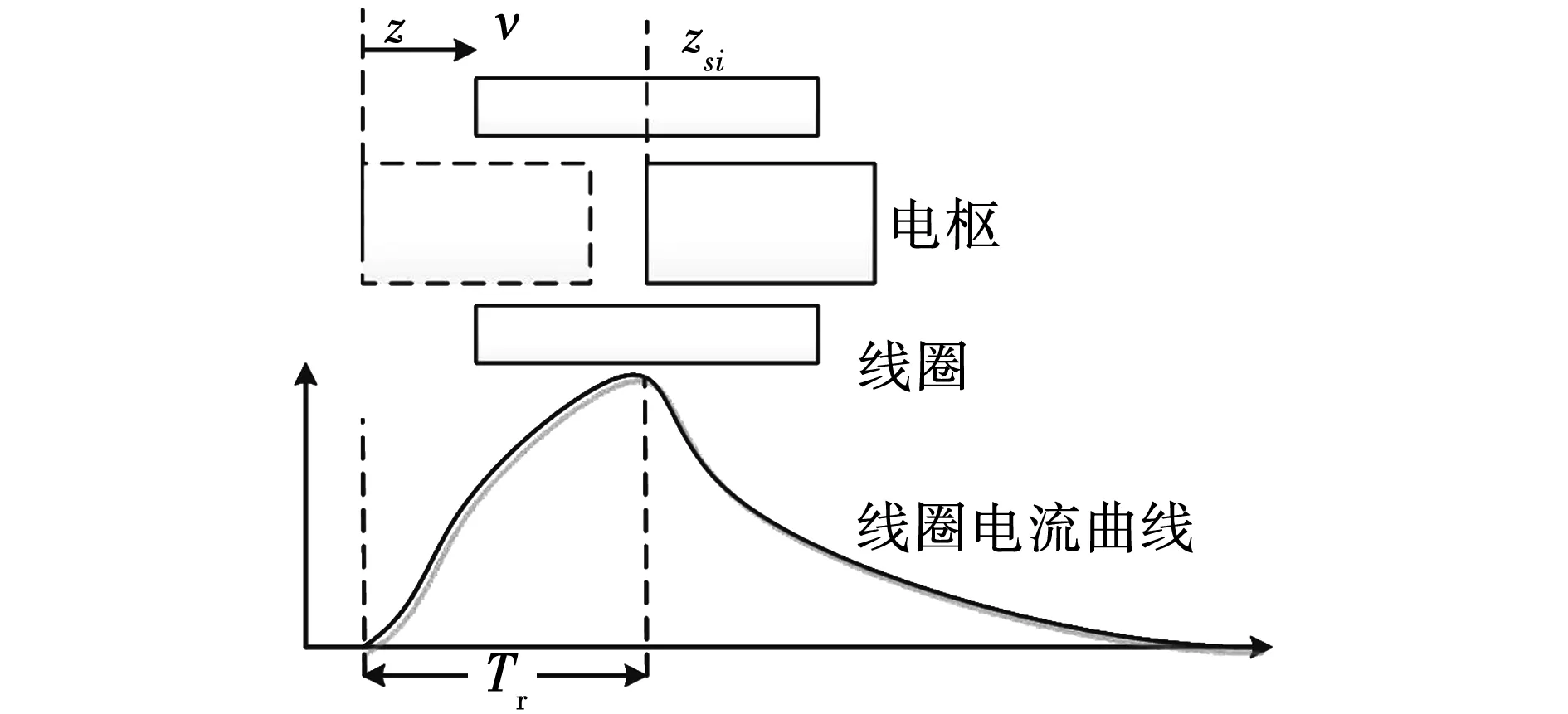
图7 触发方式示意图
(17)
式中Si是第i级线圈的晶闸管触发信号。在模型中,当某级线圈满足式(17)的触发条件,S矩阵中相对应的一位由1变为0,即从大电阻变成0。
3 仿真分析
采用前面分析方法,在MATLAB/Simulink中搭建电容驱动型多级感应线圈炮仿真程序,模型框图如图8所示。模型将脉冲回路中的晶闸管等效替换为大电阻Req,使用SFUNCITON模块建立其数学模型,计算出电枢运动的电磁推力,使用Simulink中的积分函数得到电枢的速度与位移量,经过触发策略单元,输出虚拟电阻的S矩阵,构成了完整的系统仿真模型。
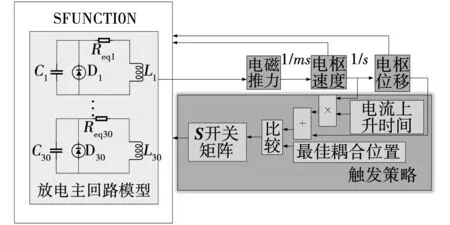
图8 线圈炮仿真模型
线圈炮系统的参数如表1所示。
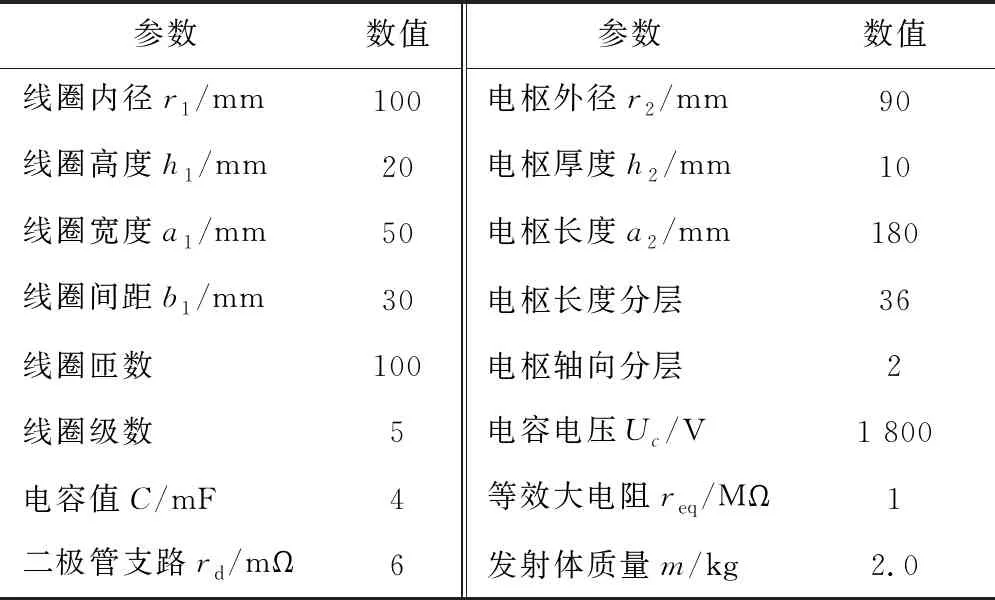
表1 线圈炮系统参数
采用有限元法提取电流丝法仿真所需的静态参数,按表1参数,n=5、m=72,Ls是5×5矩阵,采用Ansys计算线圈自感和线圈之间互感,线圈自感为220 μH,相邻线圈之间互感为75 μH,隔1个线圈之间互感为31 μH,隔2个线圈之间互感为15 μH,隔3个线圈之间互感为8.9 μH。
同理,Lr是72×72矩阵,由于参数较多,这里不再写出,电流环轴向互感曲线如图9所示。
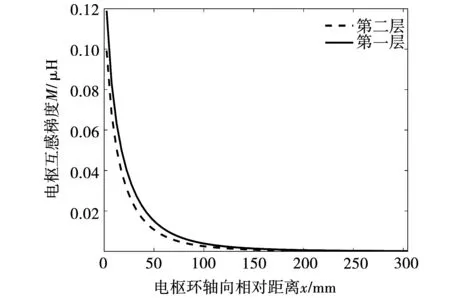
图9 电枢互感曲线
计算单个电流环与单个线圈之间的互感和互感梯度曲线如图10所示,其中,将线圈径向从外到内划分为4层计算。
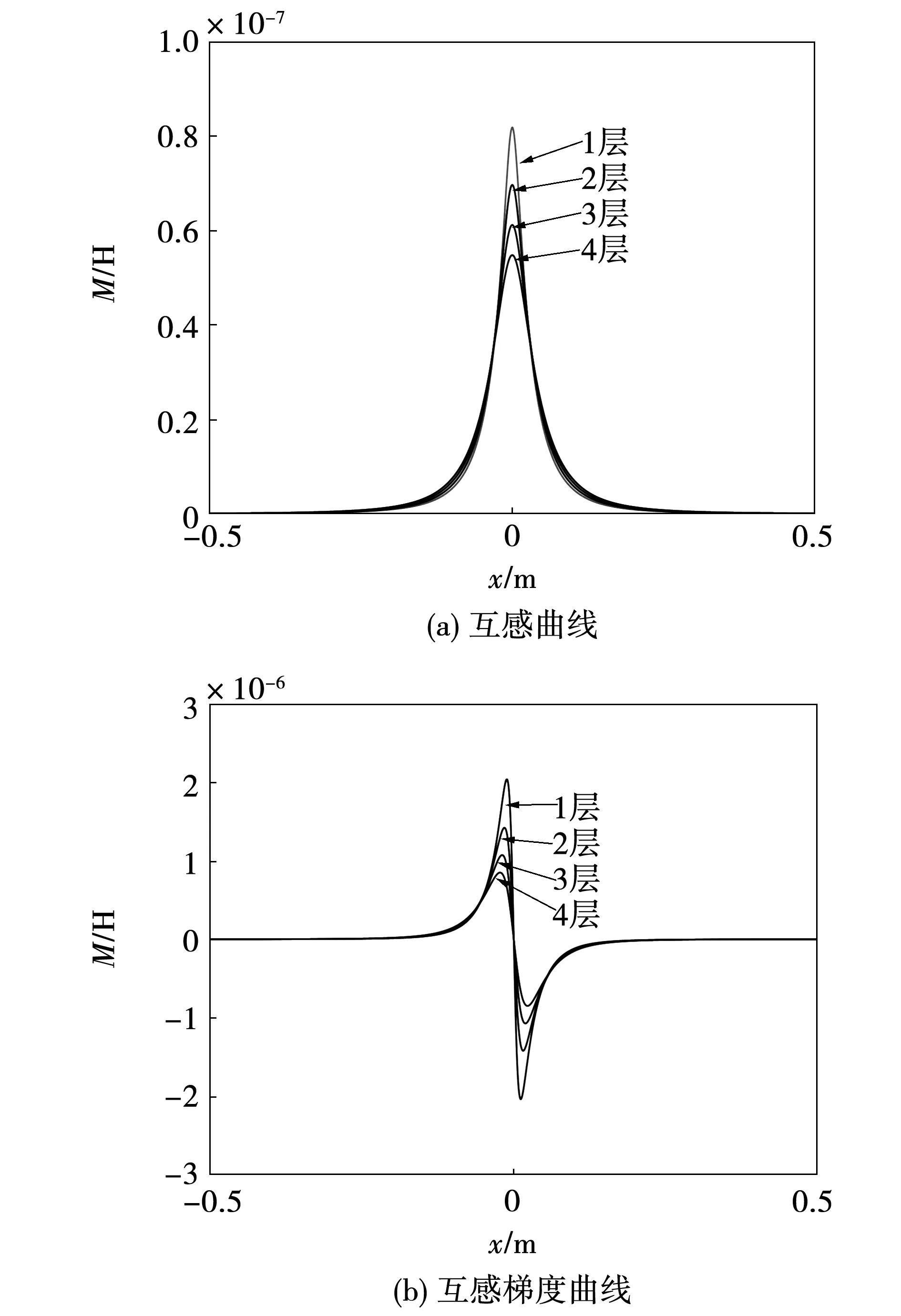
图10 电枢电流环与线圈的互感与互感梯度曲线
当电枢电流环和线圈之间轴向距离超过200 mm后,互感和互感梯度可以忽略不计。
5级线圈总长度是400 mm,线圈长度80 mm,单个线圈耦合范围在(-300,300)mm,因此线圈和电枢的互感和互感梯度矩阵只需考虑相对距离值(-380,430)mm时对应的互感及互感梯度值,将有限元中的互感结果导入到MATLAB数学模型中,直接利用矩阵进行计算,大幅减少了计算量,提升了计算速度。对整个发射过程进行仿真,并在MAXWELL有限元仿真软件中建立同样的场路耦合模型进行比较。采用式(15)改进电流丝法进行计算,触发控制策略采用式(16),根据现有装置的转换效率,预期出口速度在70 m/s。最终得到的仿真结果如图11和图12所示。
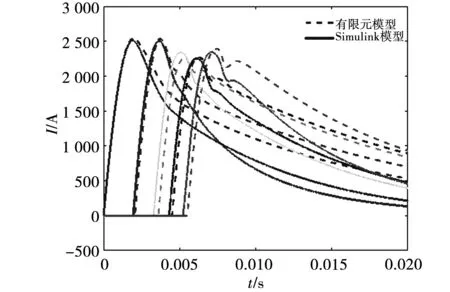
图11 各级线圈电流曲线
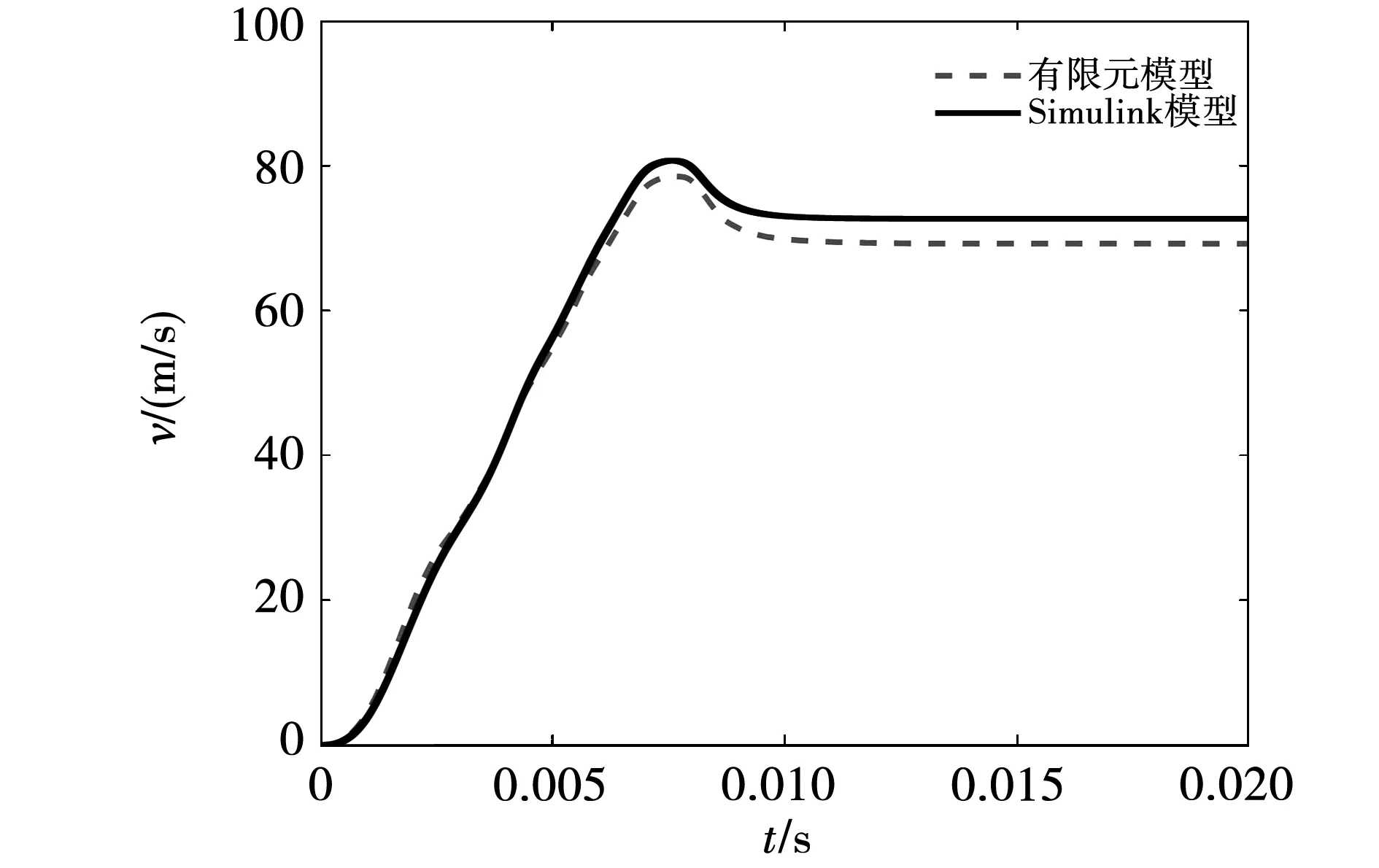
图12 电枢速度曲线
对有限元仿真模型与Simulink模型进行比较,设置相同的目标时间,Simulink模型比有限元模型仿真速度快50%。且通过仿真可以看出,脉冲回路放电过程按照逐级放电的顺序正常放电,有限元模型与Simulink模型的各级放电曲线的上升沿吻合度高,3、4、5级触发时刻有细微差别,说明两个模型中的电枢运动不是完全一致的,从图12中也可以看出,两个模型的速度曲线存在3%的误差,经分析,由于在Simulink中的电枢环以及线圈参数都是固定的,其中电枢的电阻不能像有限元精细剖分,趋肤效应考虑得并不充分,所以电流曲线在下降阶段会出现较大误差。最终仿真的出口速度达到了71 m/s,仿真结果达到了预期分析的速度。
4 实 验
通过图13所示的五级线圈发射装置实验平台对仿真模型进行验证。

图13 五级线圈发射装置实验平台
在额定电压下的各级放电电流曲线如图14所示,并与有限元放电结果进行比较。可以看出,实际放电曲线与仿真相比,上升沿出现较大误差,经分析是由于模型中的线圈参数是根据有限元中仿真计算得到,与实际线圈存在偏差,下降沿吻合度相较于两个模型之间的吻合度较好。这说明有限元模型中的模型具有更好的参考意义,Simulink模型中存在误差。
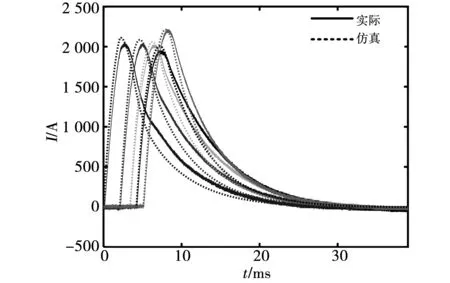
图14 实验平台五级电流放电曲线
采用光电传感器在出口测算速度,最终的速度为65 m/s,与仿真结果相差7%,存在一定误差,是由于电流曲线决定了电枢运动受力,相对于仿真模型,实际电枢受力较小。
5 结 论
通过对多级感应线圈炮的电路方程以及运动方程进行分析,对模型进行了简化,并在Simulink中搭建模型验证简化方法,结合实验进行比较,得到以下结论:
1)探讨了电容驱动型多级感应线圈炮的电流丝模型。引入等效大电阻使其合并为一个方程组,简化了模型,优化了模型计算中的非线性过程,使其利于分析和仿真计算。同时将模型中互感矩阵部分做成查表形式,避免了整体计算求逆出错的问题。与有限元计算方法相比提升了计算速度。
2)将Simulink模型与有限元模型进行比较。其中,放电电流的吻合度不高,经分析原因为两种模型剖分方法不一致,导致电流曲线出现误差,但是在连续脉冲形成的电枢受力曲线中,主要的影响因素是电流上升沿,所以两个模型的运动曲线存在较小误差。
3)通过五级线圈发射实验平台验证了模型的正确性,结果存在一定误差,但该模型对于电枢的运动分析具有一定的参考性,为之后系统提高性能、寻找最优触发策略提供了新的模型参考。
