复杂网络输出反馈量化同步控制

石宇静， 胡昌敏， 李善强

(1.福建工程学院 计算机科学与数学学院，福建 福州 350118；2. 哈尔滨理工大学 数学系，黑龙江 哈尔滨 150080)

0 引 言

复杂网络普遍存在于我们的生活以及工程中， 如万维网、互联网、生命科学[1]等。近几年， 由于复杂网络的广泛应用，复杂网络的研究吸引了越来越多学者关注。同步是复杂网络的一种普遍现象。复杂网络同步控制的方法主要包括牵制控制[2-3]、脉冲控制[4]、滑模控制[5-6]和间歇控制[7]等。

目前复杂网络同步控制的研究多数采用状态反馈控制方法。但在实际中，由于复杂网络包含众多节点以及各种条件的限制，复杂网络节点的状态往往不便测量或者测量成本过高，因此研究有效的输出反馈同步控制方法是极具现实意义的。文献[8]研究了基于状态观测器方法的复杂网络输出反馈同步控制问题， 利用Lyapunov稳定性理论，得到了保证复杂网络同步的充分条件。文献[9]研究了带有执行器饱和以及概率故障的时滞复杂网络输出反馈同步控制问题。利用Lyapunov-Krasovskii函数法和随机分析技术证明了同步误差系统和观测误差系统的渐近稳定性，并且给出了原点吸引域估计的凸优化算法。文献[10]研究了复杂网络的自适应输出反馈同步控制问题，考虑了系统执行器的偏差故障，利用线性矩阵不等式技术得到了同步误差范数有界的充分条件。

另一方面，在网络化系统中，由于信号传输过程中传输容量的限制、 数据包的有限字长等原因,通常需要对经由有限速率网络传输给下一个节点的信号进行量化。量化器的引入解决了一些数字信号不易编码的问题，同时也减轻了信息传输对网络带宽的压力。量化现象对复杂网络同步性能的影响不容忽略，因此，近些年对于复杂网络的量化同步控制问题已涌现了一些研究结果。例如，文献[11]设计了量化牵制同步控制器，其特点是控制器中不含有符号函数避免了抖动现象，并给出了复杂网络固定时间稳定的判别准则。文献[12]利用量化同步控制的方法，研究了具有不连续节点的复杂网络有限时间同步控制问题。文献[13]设计了量化间歇同步控制器，利用多重Lyapunov函数法和凸组合技术，研究了复杂网络的有限时间同步控制问题，并给出了设定时间估计的最优算法。但上述复杂网络量化同步控制的研究都是采用状态反馈控制策略，而当网络节点的状态不可测时，上述控制策略均不能适用。

基于上述分析，本文研究复杂网络的输出反馈量化同步控制问题。主要贡献可归纳如下：1)为了减轻信号传输对网络带宽的压力，采用对数量化器对控制输入信号进行量化。并利用范数有界不确定性的方法处理控制量化问题，分析量化对复杂网络同步性能的影响。2)通过设计状态观测器获得网络节点的状态估计，以该状态估计为基础给出复杂网络输出反馈量化同步控制器的设计方法。3)通过Lyapunov 稳定性理论以及线性矩阵不等式技术, 得到保证观测误差和同步误差渐近收敛的充分条件。

1 问题描述

考虑由N个节点构成的复杂网络，且第i个节点的动态模型为：

(1)

其中xi(t)∈n,ui(t)∈m,yi(t)∈q分别表示复杂网络第i个节点的状态向量，控制输入和测量输出。A∈n×n,B∈n×m,C∈q×n，且矩阵B为列满秩矩阵。g(·)∈n是一个非线性函数向量。Γ是对角的内部耦合矩阵。Φ=(φij)N×N表示外部耦合矩阵，当i≠j时，若第i个节点与第j个节点有连接，则φij>0，否则φij=0，且

令x0(t)∈n是复杂网络中孤立节点的状态，假定它是唯一的, 并且满足如下方程:

(2)

其中y0(t)∈q是复杂网络孤立节点的测量输出。

考虑系统(1)中的状态是不可测的，设计如下形式的状态观测器：

(3)

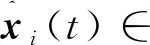
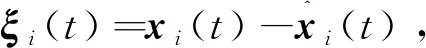
LiCξi(t)。

(4)

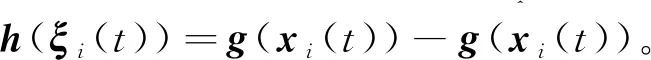
定义同步误差为ei(t)=xi(t)-x0(t)，由式(1)和式(2)可得，同步误差动态方程可以表示为

Bui(t)。

(5)

其中f(ei(t))=g(xi(t))-g(x0(t))。

假设1:对于任意的a,b∈n，非线性向量函数g(xi(t))满足以下条件：

‖g(a)-g(b)‖≤d‖a-b‖,

其中d≥0是一个已知的常数。

引理1[14]对于任意的两个向量x,y∈n，有下列不等式成立：

xΤy+yΤx≤λxΤx+λ-1yΤy。

其中λ>0是一个常数。

引理2[15]M,N,F是具有适当维数的实矩阵，且F满足FΤF≤I，那么对于任意的标量ε>0，有

MFN+NΤFΤMΤ≤ε-1MMΤ+εNΤN。

2 量化同步控制器设计

令φ(·):→为对数量化器，其中={±ωi:ωi=ρiω0,i=±1,±2,…,}∪{±ω0}∪{0}，且ω0>0。对于∀τ∈，相应的对数量化器可表示为：

(6)

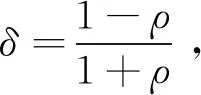
对于第i个节点，设计如下量化控制器：

(7)

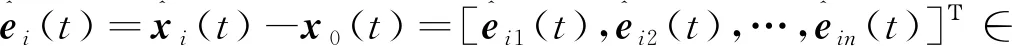
又由式(6)可得

[In+Λi](ei(t)-ξi(t))。

(8)

其中Λi=diag{Λi1,Λi2,…,Λin}，且Λij∈[-δi,δi]。

根据式(8)，量化控制器式(7)可以进一步表示成如下形式：

ui(t)=-Ki[In+Λi]ei(t)+Ki[In+Λi]ξi(t)。

(9)

将式(9)代入式(5)，则同步误差系统可以改写为

BKi[In+Λi]ei(t)+

BKi[In+Λi]ξi(t)。

(10)

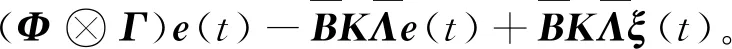
(11)

由于矩阵B∈n×m列满秩，即rank(B)=m，则有那么存在正交矩阵U∈Nn×Nn，V∈Nm×Nm使得下列等式成立：

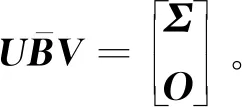
(12)

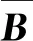
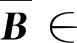
(13)

其中P11>0∈Nm×Nm，P22>0∈N(n-m)×N(n-m)，则存在非奇异矩阵R∈Nm×Nm使得

另外，容易得到观测误差动态系统(4)的增广形式为

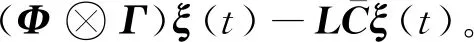
(14)

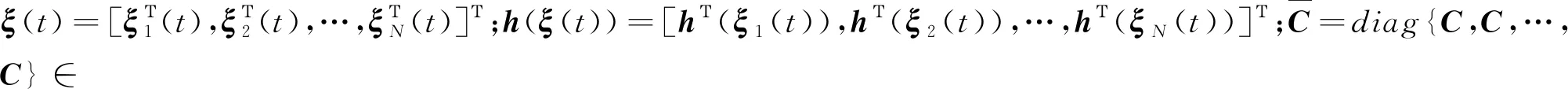
若令η(t)=[eΤ(t)ξΤ(t)]Τ，由式(11)和式(14)可得如下闭环系统方程：

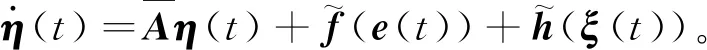
(15)

其中

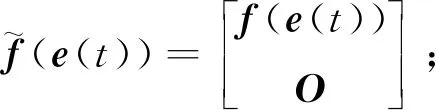
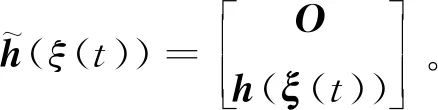
3 主要结果

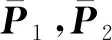
(16)

其中

(IN⊗AΤ+ΦΤ⊗Γ)P1-

(IN⊗AΤ+ΦΤ⊗Γ)P2-

则在量化控制器(7)的作用下闭环系统(15)渐近稳定，且控制器和观测器增益矩阵分别为

证明：选取如下Lyapunov函数

V(t)=ηΤ(t)Pη(t)

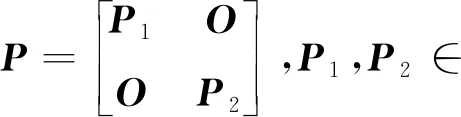
(17)

由假设1可知：

‖f(ei(t))‖=‖g(xi(t))-g(x0(t))‖≤

di‖xi(t)-x0(t)‖=

di‖ei(t)‖。

从而有

eΤ(t)(D⊗In)e(t)。

(18)

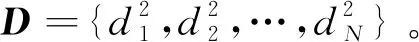
hΤ(ξ(t))h(ξ(t))≤ξΤ(t)(Θ⊗In)ξ(t)。

(19)

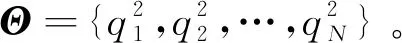
(20)

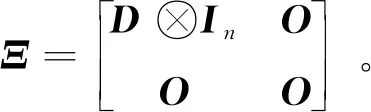
(21)

将式(20)和式(21)代入式(17)，则有：

λ1Ξ+λ2Q]η(t)=ηΤ(t)Ωη(t)。

(22)

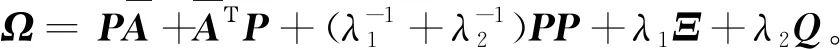
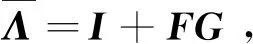
(23)

其中

(IN⊗AΤ+ΦΤ⊗Γ)P1-

根据引理3可知，存在非奇异矩阵R∈Nm×Nm使得由式(12)和式(13)可得

即有：

因此R=(VΤ)-1Σ-1P11ΣVΤ，由此可得：

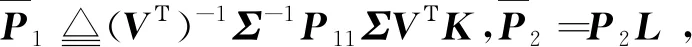
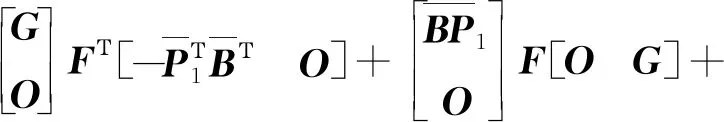
(24)

其中

由式(24)，应用Schur补引理可知，若有下面的不等式成立，则可保证Ω<0。

(25)

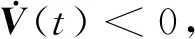
4 仿真

根据文献[17]，考虑由5个蔡氏电路构成的复杂网络。单个蔡氏电路如图1所示，且其动态方程描述如下：

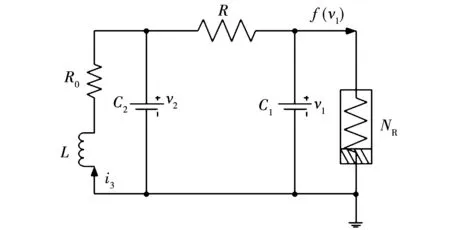
图1 蔡氏电路

其中：v1、v2分别表示电容C1、C2两端的电压；i3表示通过电感器L的电流；R0、R是线性电阻；f(v1)表示通过非线性电阻NR的电流，且

f(v1)=Gb1v1+0.5(Ga1-Gb1)(|v1+1|-|v1-1|)。

根据文献[18]，将反馈控制与电感串联构成电源u(t)，因此复杂网络可以表示成如下形式：

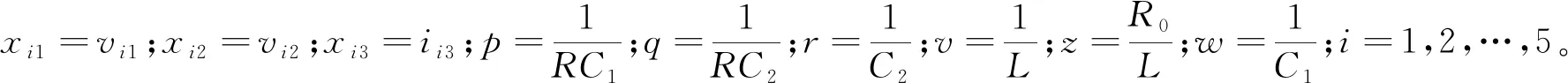
令复杂网络的外部耦合矩阵为：

如文献[18]，选择p=9.1，q=1，r=1，Gb1=-0.755 9，Ga1=-1.393 86，v=16.581 1，z=0.138 083，w=0.09。选择量化密度ρ=0.7，参数d=0.039，q=0.033。选择内部耦合矩阵为Γ=diag{0.05,0.05,0.05}以及网络各个节点和孤立节点的初始状态分别为：

x1(0)=[0.01,-0.01,0]T；

x2(0)=[0.03,-0.02,-0.05]T；

x3(0)=[0.07,-0.02,-0.03]T；

x4(0)=[0.01,-0.02,0]T；

x5(0)=[0.03,0.02,-0.05]T；

x0(0)=[0.02,0.01,-0.01]T。

首先, 考虑不对复杂网络施加控制的开环响应如图2所示，从图2可见开环情况下同步误差轨迹是发散的。

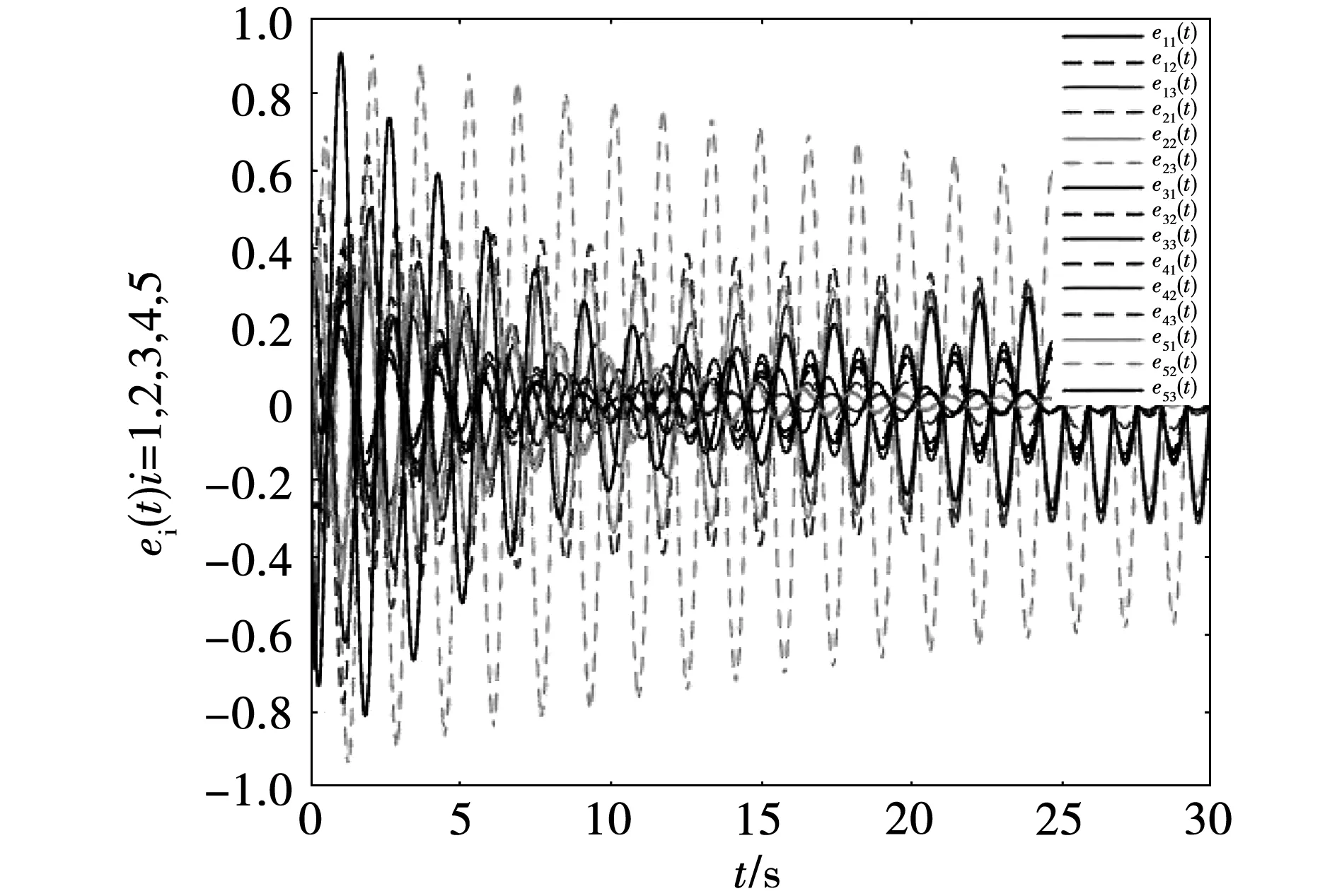
图2 开环轨迹

然后，将量化输出反馈同步控制器式(7)作用于蔡氏电路网络，且选择观测器的初始状态为：

ξ1(0)=[0.01,-0.01,0]Τ；

ξ2(0)=[0.03,-0.02,-0.05]Τ；

ξ3(0)=[0.07,-0.02,-0.03]Τ；

ξ4(0)=[0.01,-0.02,0]Τ；

ξ5(0)=[0.03,0.02,-0.05]Τ。

利用MATLAB LMI工具箱, 通过求解线性矩阵不等式(16)，根据定理1可求得观测器增益矩阵为：

以及控制器增益矩阵为：

观测误差以及同步误差在控制器(7)作用下的闭环轨迹如图3和图4所示。根据图3和图4发现可知观测误差动态以及同步误差动态系统均可在量化输出反馈控制器(7)的作用下达到渐近稳定。

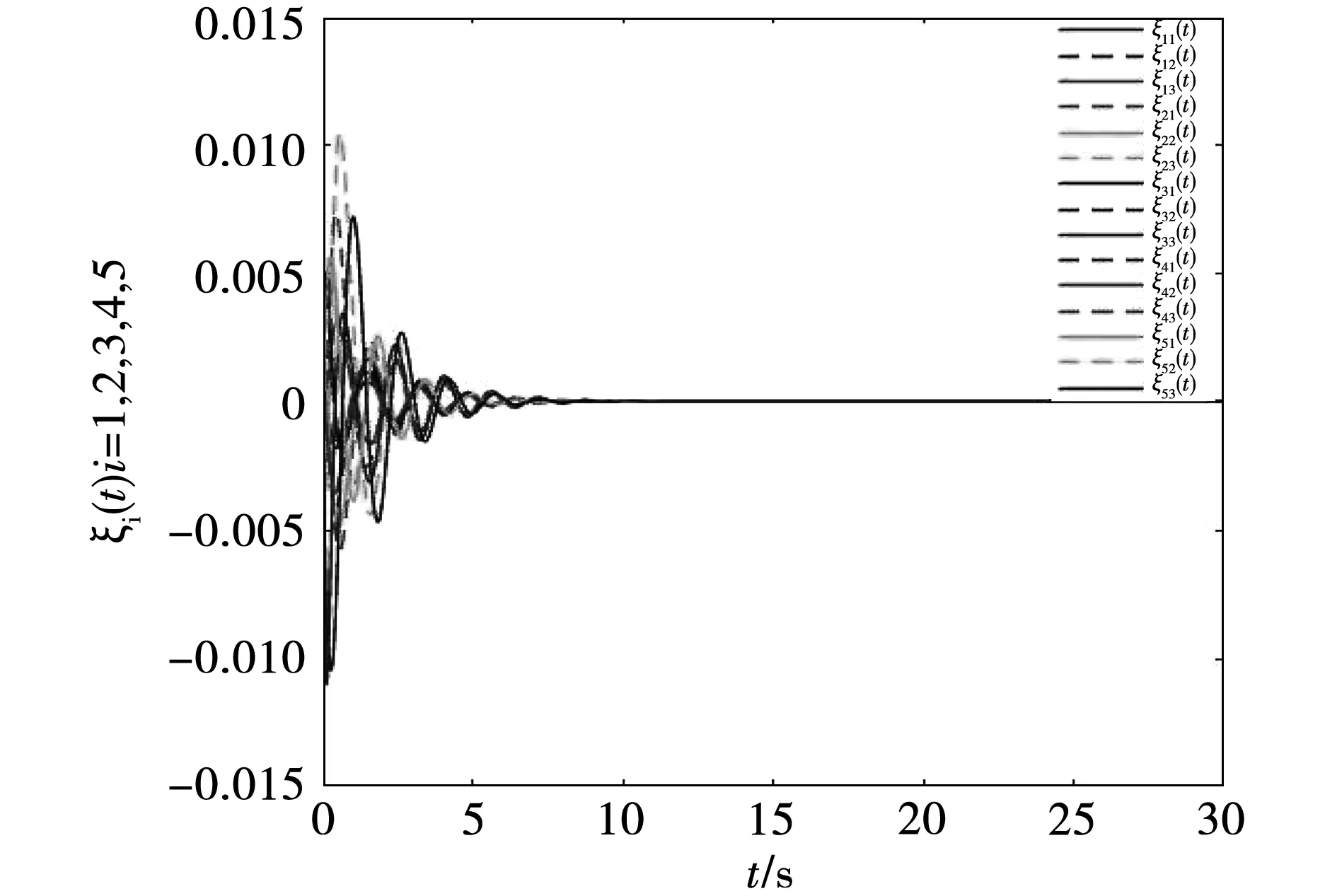
图3 观测误差闭环轨迹

为了进一步说明本文所给控制方法的有效性，将本文设计的控制方法与文献[19]中的控制方法进行对比。文献[19]的自适应控制器与自适应更新律分别为如下形式：

ui(t)=-di(t)CΤεi(t)(1+‖εi(t)‖2(p-1))；

(26)

(27)

其中：εi(t)=yi(t)-y0(t)表示输出误差；di(t)是控制器的自适应增益，i=1,…,N，p为正整数，κk为正常数。仿真时选择参数κk=5，p=1，则在控制器式(26)，式(27)的作用下，复杂网络同步误差的轨迹如图5所示。

比较两种控制方法的同步误差轨迹图4和图5，可见在控制器式(26)，式(27)的作用下，复杂网络的同步误差达到稳定的时间需要20 s，而利用本文设计的控制器只需要8 s，即利用本文所给的控制方法复杂网络同步误差收敛的速度更快。

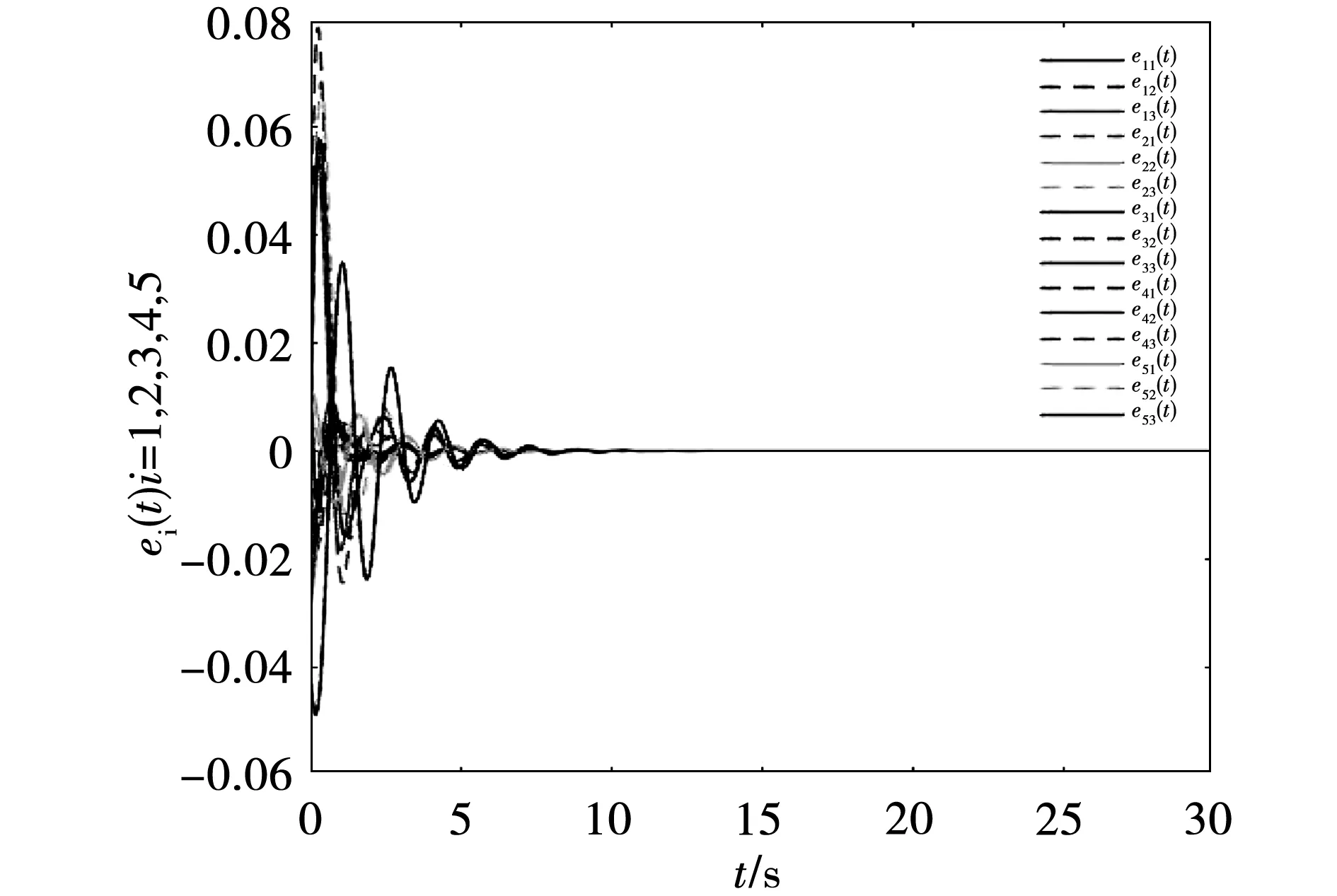
图4 同步误差闭环轨迹

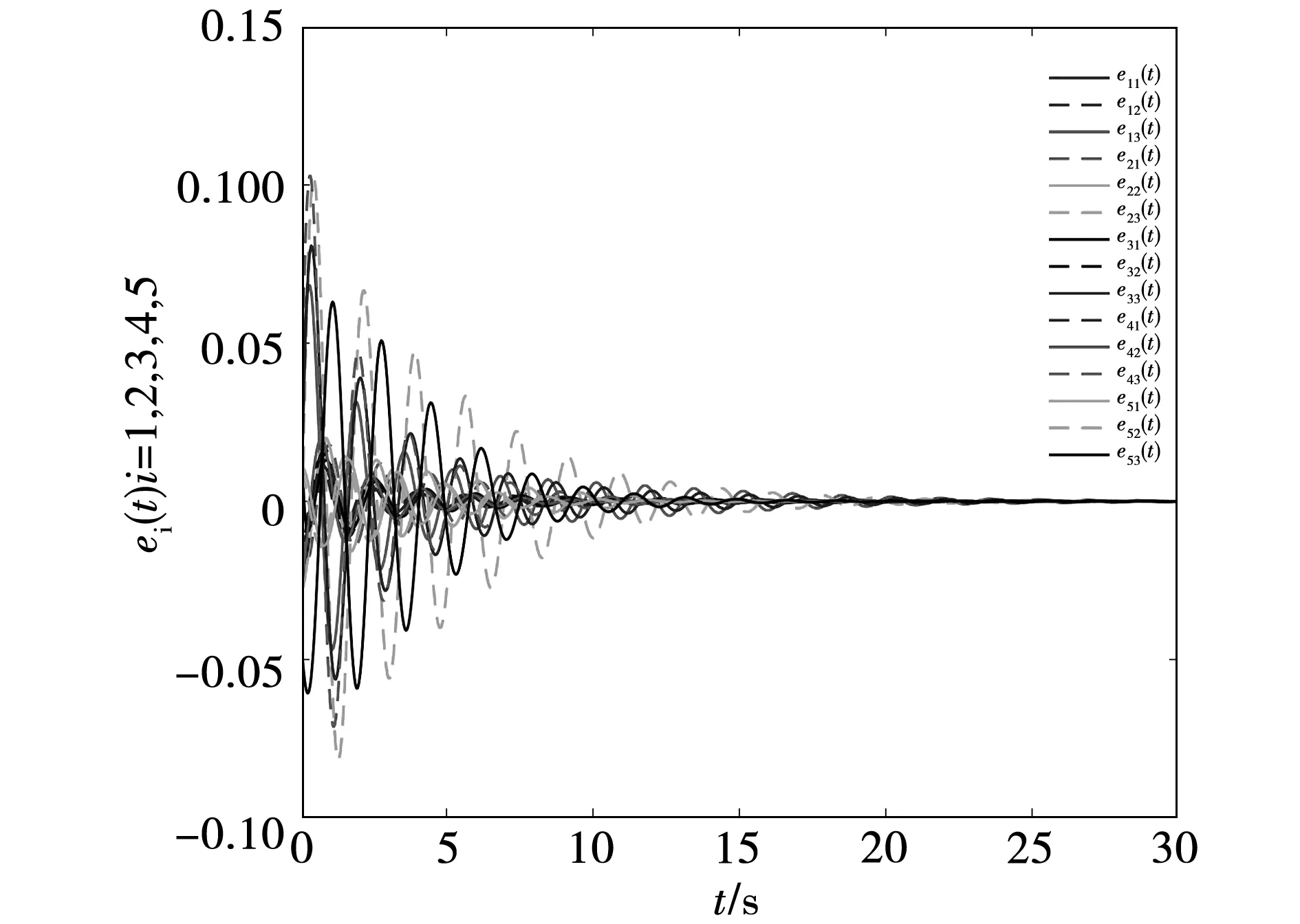
图5 采用文献[19]控制方法的同步误差轨迹

5 结论

本文主要研究了复杂网络的量化同步控制问题。基于状态观测器，设计了带有对数量化的输出反馈同步控制器。应用LMI技术给出了求解观测器增益矩阵以及控制器增益矩阵的计算方法。利用Lyapunov稳定性理论，证明了观测误差动态系统以及同步误差动态系统的渐近稳定性。最后，通过蔡氏电路仿真实验验证了所提控制方法的可行性和有效性。