磁集成双Buck/Boost-LLC三端口DC-DC变换器
2022-06-23李洪珠罗帅
李洪珠, 罗帅
(辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105)
0 引 言
近年来新型清洁能源发电系统由于受环境影响较大,为了产生稳定的电能,引入缓冲单元的新能源联合供电技术不断发展[1-2]。因此,在光伏、风能和蓄电池等混合发电系统中,一个多端口变换器可以取代多个传统二端口变换器进行不同端口间连接[3-4],实现低成本、集中控制、结构简单等优点。
国内外学者致力于多端口DC-DC变换器拓扑结构的改进与完善,文献[5]提出了三端口变换器(three-port converter,TPC)的通用结构图,在光伏端引入蓄电池储能装置作为缓冲单元,与负载端构成了一个TPC。文献[6-7]根据隔离特性,将多端口DC-DC变换器的拓扑结构按非隔离型、部分隔离型和完全隔离型分类。文献[8-10]通过多绕组变压器磁耦合方式集成一个多端口变换器,各个端口间实现了隔离,但器件较多,控制复杂。文献[11-12]提出了全桥隔离型TPC,利用全桥功率开关管的复用,减少了功率器件,但增加了磁性元件的数量和体积。
本文提出一种磁集成双Buck/Boost-LLC三端口DC-DC变换器,在全桥LLC谐振变换器的一次侧集成了两相并联双向Buck/Boost变换器,减少功率元件的数量、实现集中控制;并利用磁集成技术将原边一侧的两个Buck/Boost电感反向耦合集成,同时与LLC谐振电感解耦集成,以实现耦合电感均流、提高功率密度、缩小TPC整体体积;同时该隔离型TPC可实现原边开关管的零电压(zero-voltage switching,ZVS)开通和副边整流管的零电流(zero-current switching,ZCS)关断技术,降低TPC开关损耗。
1 三端口DC-DC变换器
1.1 拓扑结构
双Buck/Boost-LLC直流型TPC的电路拓扑如图1所示。利用功率开关管Q1~Q4的复用,且引入两电感L1、L2接在谐振槽A、B端,集成了两个并联双向Buck/Boost变换器,根据开关管的导通特性,两并联双向Buck/Boost变换器交错180°运行。
1.2 工作模式
磁集成双Buck/Boost-LLC直流型TPC根据其功率流动方向可分为两种工作模式:
1.2.1 Buck-LLC模式
Buck-LLC模式的功率流动如图2所示,Vs作为输入端,定频调节开关管Q1和Q2的占空比DBuck,一次侧双向Buck/Boost变换器工作在Buck模式,功率从Vs端向Vb端流动;定占空比调节开关管开关频率fs,功率经LLC变换器向Vo端流动。
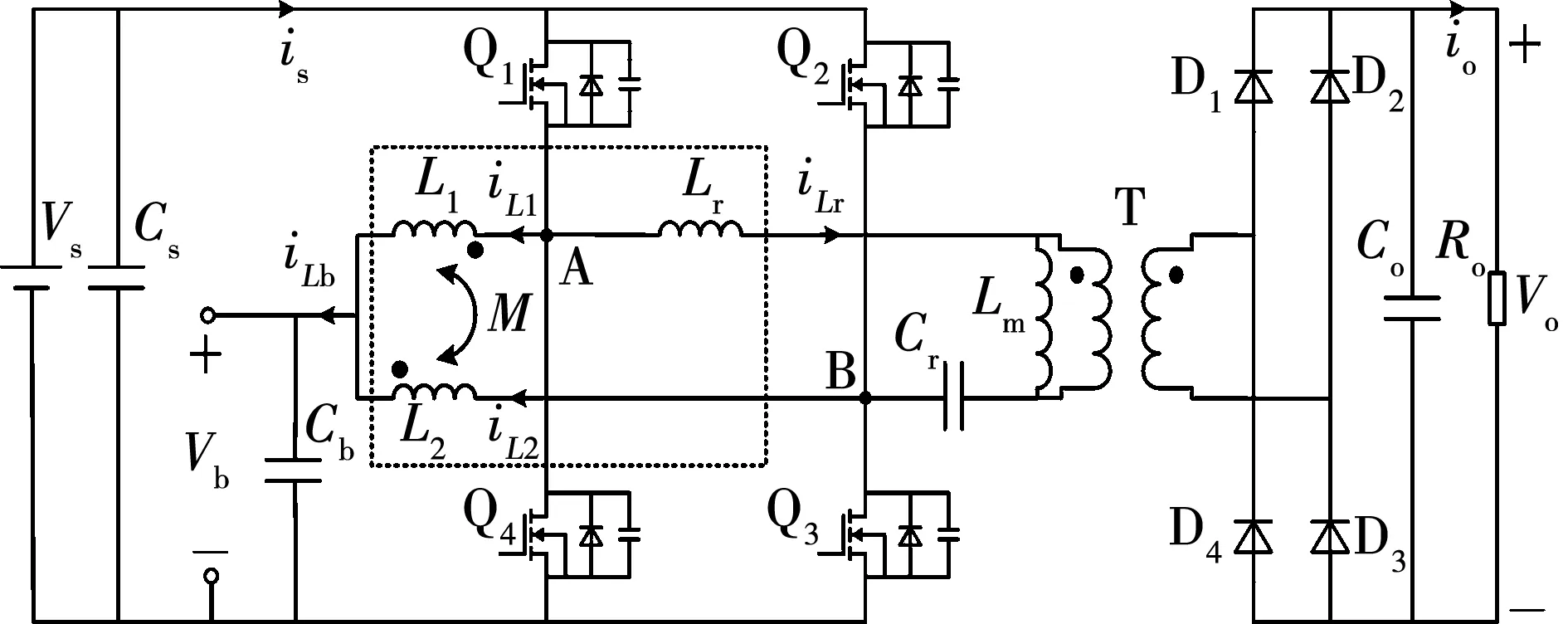
图2 Buck-LLC模式功率流动图
1.2.2 Boost-LLC模式
Boost-LLC模式的功率流动如图3所示,Vb作为输入端,定频调节开关管Q3和Q4的占空比DBoost,一次侧双向Buck/Boost变换器工作在Boost模式,功率从Vb端向Vs端流动;定占空比调节开关管开关频率fs,功率经LLC变换器向Vo端流动。
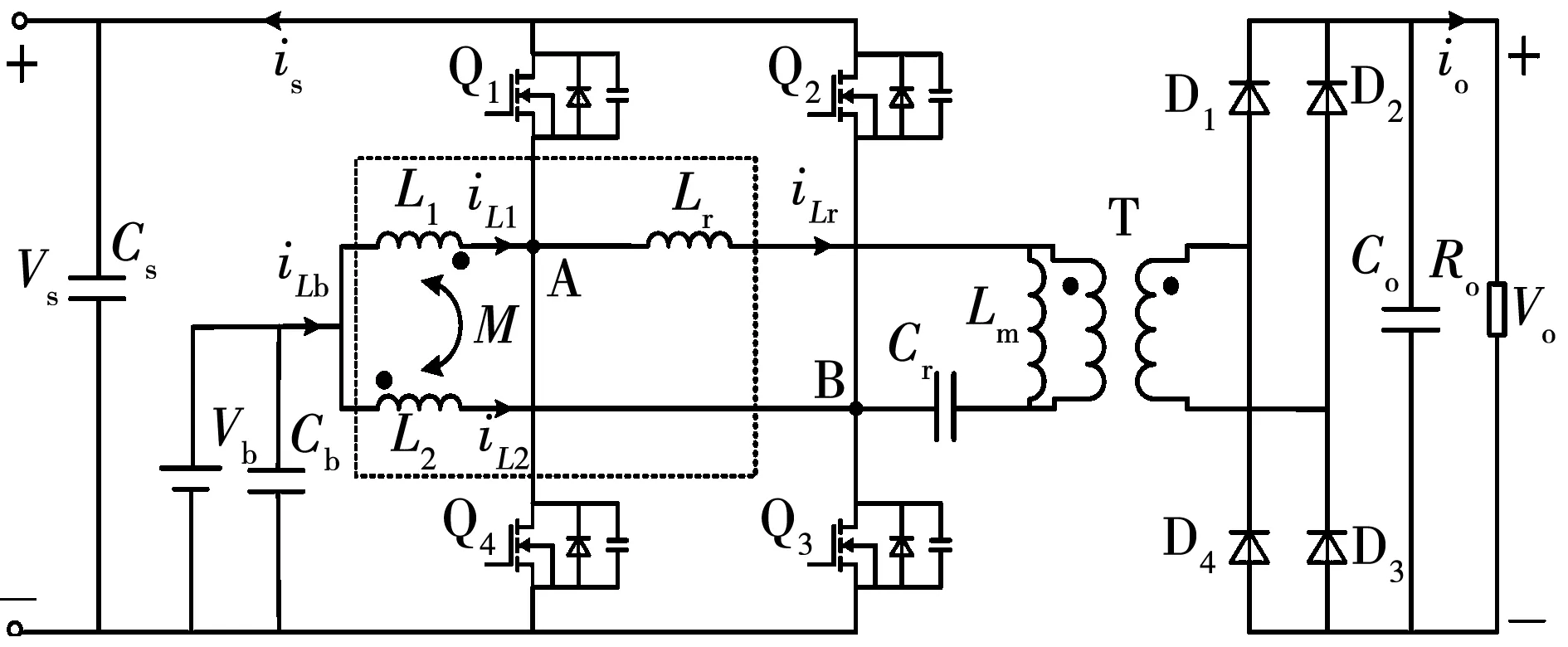
图3 Boost-LLC模式功率流动图
1.3 工作原理
以Buck-LLC模式为例,对该直流型TPC的控制及模态进行详细分析。
1.3.1 控制分析
通过脉冲宽度调制(pulse width modulation,PWM)调节占空比DBuck控制时,一次侧双向Buck/Boost变换器功率从Vs流向Vb。DBuck<0.5时,部分电流波形如图4所示,tdead为死区时间,两并联Buck/Boost电感L1、L2理论数值相等,开关管Q1和Q2交错导通,其电流波形交错互补,总输出电流iLb纹波大部分得到抵消;DBuck>0.5时,情况与DBuck<0.5类似;而DBuck=0.5时,电感L1、L2电流波形互补对称,总输出电流iLb纹波得到完全抵消。为了使双向Buck/Boost变换器电感总电流纹波达到最小,本文控制DBuck为0.5。

图4 DBuck<0.5时Buck/Boost电路部分电流波形
通过脉冲频率调制(pulse frequency modulation,PFM)调节开关管频率fs控制时,功率从母线电压Vs向Vo流动。LLC变换器的谐振槽存在两个谐振频率点fr1和fr2,表达式为:
(1)
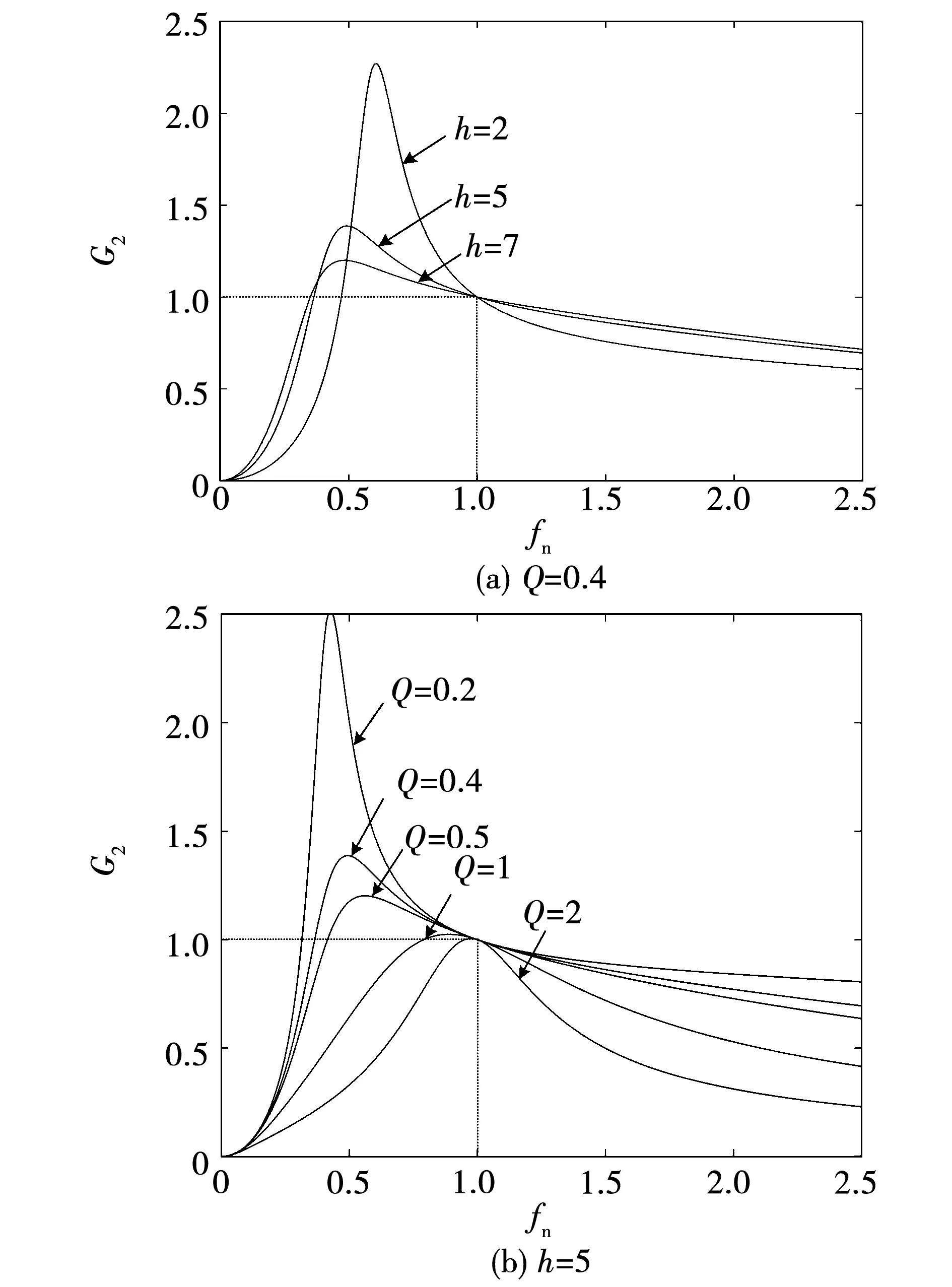
根据频率fs的变化区间,LLC谐振变换器分为三种不同的工作状态:次谐振区域(fr2 1.3.2 模态分析 结合上述控制分析,本文采用定占空比调频的控制策略(DBuck=0.5及fr2 图5 直流型TPC稳态波形图 图6 (t0~t4)阶段的等效电路 1)模态1(t0~t1)。 t0时刻,在驱动信号控制下开关管Q1、Q3导通,Buck/Boost电感L1、L2开始充、放电,电流iL1线性上升,iL2线性下降;谐振槽施加正向输入电压uAB,电流iLr先经过Q1、Q3的反并联二极管续流,减小到0后开始正向增大,Lm两端电压为nVo,电流iLm线性上升,且iLr>iLm;变压器二次侧电流经过整流管D1和D3导通。此阶段谐振槽的谐振频率为fr1。 2)模态2(t1~t2)。 t1时刻,iLr与iLm相等,Lm将不再被限制和Lr、Cr一起发生谐振,此阶段变压器没有功率传输,流经二次侧整流管D1和D3的电流到0后自然关断,实现ZCS技术。此阶段谐振槽的谐振频率为fr2。 3)模态3(t2~t3)。 t2时刻,开关管Q1、Q3同时关断,Q2、Q4仍未导通,系统处于死区时间tdead内,即所有的开关管全部关断。uAB逐渐减小至0,iLr和iLm也开始减小;iLr给开关管Q1、Q3的输出电容充电,开关管Q2、Q4的输出电容开始放电,此阶段通过电容充放电来保证系统正常工作。 4)模态4(t3~t4)。 t3时刻,开关管的输出电容充放电完成。iLr经过开关管Q2、Q4的反并联二极管续流,使得其正向压降为0,为ZVS开通提供条件。uAB开始反向增大,此时iLr 5)t4时刻,开关管Q2、Q4导通,TPC开始工作在下半个周期(t4~t8),与t0~t4阶段对称。Boost-LLC模式与Buck-LLC模式原理类似,在此不再赘述。 该直流型TPC包括两个非隔离双向Buck/Boost变换器和一个隔离单向LLC谐振变换器,因此存在两个电压增益,分别为G1、G2。 通过PWM控制,易得双向Buck/Boost变换器的电压增益为: (2) 通过PFM控制,用基波近似法[15](fundamental harmonic approximation,FHA)分析全桥LLC谐振变换器的电压增益为 (3) 直流电压增益G2的关系曲线如图7所示,可以看出,G2与h、Q、fn均有关,且存在两个普遍规律: 1)随着fn的逐渐增大,无论h、Q值如何变化,电压增益G2都先增大后减小,且都有一个对应的峰值点; 2)当fn=1,即fn=fr1时,G2始终为1。 由图7(a)可知,Q值一定时,电感比值h越小,电压增益越高,调频特性较好,但会增大磁件损耗;由图7(b)可知,h值一定时,Q值越小,调频特性越好,但会提高一次侧电流,损耗增加,效率降低,因此h、Q值的选取要综合考虑。同时在次谐振区域内(fn<1),通常选取最高增益处到归一化频率处的频率范围来调节电路电压增益G2。 图7 直流增益特性 利用磁集成技术将该直流型TPC的两个交错并联Buck/Boost电感L1和L2反向耦合,并与LLC谐振电感Lr解耦集成在一起,磁芯结构如图8所示。 通过绕组间耦合作用完全抵消的原理实现L1和Lr两电感解耦集成[16]的磁路模型如图9所示。 图9 电感L1和Lr解耦集成的磁路模型 从图8可以看出,LLC谐振电感Lr绕在磁芯中柱上,匝数为N;Buck/Boost电感L1同时绕在磁芯的两个侧柱上,匝数分别为N1、N1′。中柱绕组磁通φ与左侧柱绕组磁通φ1方向相反,与右侧柱绕组磁通φ1′方向相同,两侧柱绕组磁通在中柱上相互抵消,以此来解除耦合作用。 图9中,R11、R12、R2为磁芯磁柱上的磁阻,Rg11、Rg12、Rg2为磁芯气隙的等效磁阻,简化磁路中有: (4) 电感L1通过电流iL1,在电感Lr中产生磁链为 (5) 电感Lr通过电流iLr,在电感L1中产生磁链为 (6) 当Φ12=Φ21=0时,电感L1和Lr实现解耦,即: (7) 但此时两侧柱的磁通密度相差会很大,左、右侧柱的磁通密度B1、B2分别为: (8) 选用“EE”完全对称型磁芯,两侧柱截面积A1、A2相等,左右侧柱气隙相同,磁阻Rm1、Rm2相等,则B1 Lr和L1、L2两电感同时解耦集成的绕组结构如图8所示,结合上述电感Lr和L1两电感解耦基础,电感L2也同时串联绕在磁芯的两个侧柱上,其中L2左右侧绕组匝数分别为N2′、N2。结合式(7),此时解耦的条件为: (9) 相比较两电感解耦集成,左右侧柱磁通密度不均衡的缺点,此时图8绕组结构左右侧柱的磁通密度B1′、B2′分别为: (10) 从上式看出B1′=B2′,图8绕组结构不仅实现Lr和L1、L2两电感同时解耦,而且克服两电感解耦集成两侧柱磁通分布不均,磁芯利用率低的缺点。 2.2.1 原理分析 结合图8绕组结构及式(9),电流iL1和iL2从耦合线圈的一对异名端流入,两线圈总匝数N1+N1′、N2+N2′相等,电感L1和L2沿最外圈磁路反向耦合,实现耦合电感均流特性[18-20],磁路模型如图10所示。 图10 电感L1和L2反向耦合的磁路模型 理想状态下,各参数完全一致,L1=L2,电流iL1与iL2流入电感L1和L2后,在磁芯磁路中产生的磁通相互抵消。实际中,L1和L2会存在偏差,两相电感电流大小不再相等,假设实验过程中因外界因素导致电感L1突然增大,则电流iL1突然减小,根据楞次定律,边柱磁芯将产生防止φ1和φ1′突然减小的顺时针感应磁通,从而产生感应电动势,在感应电动势作用下iL1逐渐增大,iL2逐渐减小,直到iL1与iL2相等。电感L1和L2反向耦合实现均流也保证了式(10)中B1′=B2′,从而实现平衡左右侧柱磁通。 2.2.2 耦合度分析 由图1可知,电感L1和L2之间互感为M,两端电压V1、V2分别为: (11) 图11为电感L1、L2一个开关周期的模态电压图,其中: (12) 根据式(11)及图11,忽略死区时间,由伏秒平衡原理得开关管Q1、Q3导通时,有 图11 电感L1、L2的模态电压图 (13) 结合图5,认为iL1在稳态时的每个开关周期内变化量均为0,通过式(11)得到耦合状态的稳态相电流纹波ΔIL1,即峰峰值为 (14) 电感L1和L2解耦条件下,即非耦合状态下的稳态相电流纹波为 (15) 式中:L1_dis为解耦时电感值,L1_dis=L+M。通过式(14)和式(15)得到相电流纹波之比为 (16) 式中k为耦合系数,k=M/L,由于是反向耦合,则-1≤k<0。 电感L1相电流纹波比值在不同占空比D下与耦合系数k的关系曲线如图12所示,可以看出比值始终小于1,即耦合状态时电感相电流纹波小。因为该TPC控制占空比D始终为0.5,可得两电感耦合系数k越接近-1,即反向全耦合时,电流纹波越小。 图12 稳态相电流纹波比 为了验证理论的正确性,搭建了一台Vs=120 V、Vb=60 V、Vo=24 V,LLC谐振变换器输出功率300 W的实验系统如图13所示,实验样机的具体指标如表1所示,一次侧选用IRF640型开关管,二次侧选用RHRP3060型二极管。 表1 实验具体指标 Buck/Boost电感L1、L2与LLC谐振电感Lr分立磁件与集成磁件的对比如图13(b)所示,测得三个分立磁芯总体积为15.52 cm3,集成磁件体积为9.52 cm3,减少了38.66%。 图13 实验系统 该直流型TPC分别工作在Buck-LLC模式和Boost-LLC模式下,一次侧双向并联Buck/Boost变换器交错180°运行时,分立电感与耦合电感电流波形及输出电压波形如图14和图15所示。为了能明显看出对照效果,通过PWM控制开关管均以0.5的占空比运行,可以看出,两种模式下分立磁件和集成磁件均可输出稳定的电压,但集成磁件中两电感L1、L2反向耦合实现了良好的均流特性。 图15 Boost-LLC模式Boost电路输出波形 集成磁件下两种模式中LLC谐振变换器工作在轻载及满载时的实验波形如图16和图17所示,其中图16(a)和图17(a)均为开关管的导通波形,经过轻载到满载实验,可以看出开关管均可以实现ZVS工作。 图16 LLC轻载(10%满载)实验波形 图17 LLC满载实验波形 图16(b)和图17(b)均为集成磁件中解耦集成的谐振电感电流波形、开关管Q4两端电压波形和输出电压波形。可以看出,谐振电感电流轻载时近似为三角波,谐振槽输入电压在轻载和满载时均为矩形波,且均可实现LLC谐振变换器稳定地输出电压。证明谐振电感解耦集成后,通过PFM控制,LLC谐振变换器可以实现正常工作。 实际在新能源混合发电系统中,双向Buck/Boost变换器的Vs端和Vb端,当其中一端参数出现变化时,都会导致一次侧全桥母线电压的改变,此时可通过式(3)调节开关管频率,改变LLC谐振变换器的电压增益,实现稳定地输出电压。 本文针对双Buck/Boost-LLC直流型TPC,引入磁集成技术,对两并联Buck/Boost电感反向耦合集成,并对耦合原理及耦合度进行分析,同时与LLC谐振电感进行解耦集成与分析,结合变换器工作原理及实验验证得到以下结论: 1)该TPC实现一次侧全桥功率开关管的复用,减少了功率开关管的数量,实现集中控制,且实验验证了本文1.2节中两种功率流动模式均可正常工作。 2)集成磁件中,两Buck/Boost电感反向耦合,耦合系数k=-0.987,相比于分立磁件实现了耦合均流特性;谐振电感Lr解耦集成后,可以平衡磁芯两侧柱磁通,实现LLC谐振变换器正常工作。 3)该变换器可以实现软开关技术,开关损耗得到降低,并以低输入电流纹波的优点应用于新能源混合发电系统中。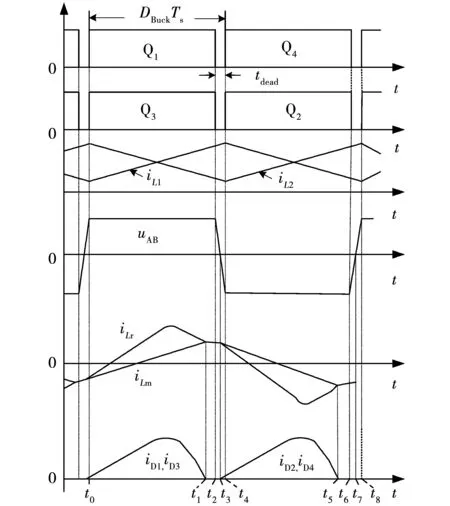

1.4 增益特性
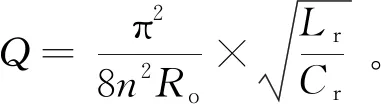
2 变换器磁集成分析
2.1 解耦集成分析

2.2 反向耦合分析




3 实 验





4 结 论
