探寻作图本质 明晰作法之理

万涛

[摘  要] 尺规作图是考查学生动手实践的数学思维能力和运用数学知识解决问题的能力，试题主要考查学生明晰尺规作图的作图原理.这给我们的教学启示是在课堂教学时可以对同一道尺规作图题进行深刻的剖析，不断优化作图的方法，增强学生与数学知识之间的关联，训练学生思维的发散性，提升学生的数学核心素养.

[关键词] 尺规作图;作图原理;发散思维

尺规作图是在学生已有的认知基础上和所具备的基本活动经验的前提下，考查学生动手实践的数学思维能力和运用数学知识解决问题的能力. 这种考查能使学生明晰尺规作图的原理，构建数学知识之间的联系，培养学生的发散性思维[1]. 下面针对2021年南京市中考数学试题第25题，和大家一起探讨这道题的作图原理，同时思考教师如何在课标的引领下，提升学生尺规作图的能力，使得学生学会分析问题，明晰作图原理.

试题呈现

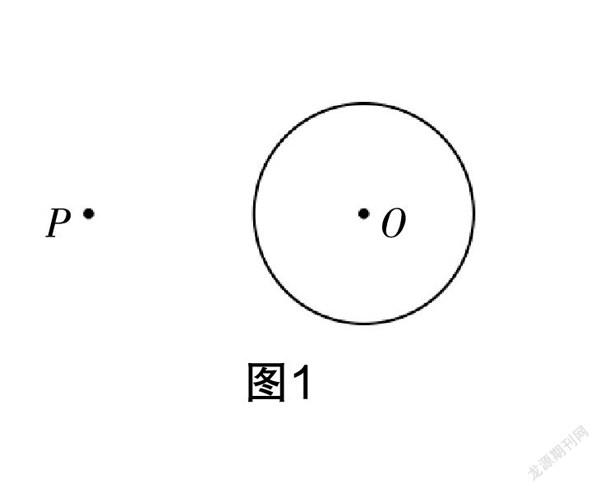
如图1，已知P是☉O外一点，用两种不同的方法过点P作☉O的一条切线. 要求：（1）用直尺和圆规作图;（2）保留作图痕迹，写出必要的文字说明.

试题分析

这是一道尺规作图题，要求学生只用直尺和圆规，过点P作☉O的一条切线. 要确定切线，根据两点确定一条直线，已知点P，关键在☉O上找一个点（即点B），使得满足直线PB与☉O相切.

本题简洁明了，但立意较高，学生感觉困难的主要原因是不理解尺规作图的原理，找不到目标图形，在有限的时间内，部分学生难以形成正确的思路，该如何突破尺规作图的思维屏障，该怎么想？方法是什么？要解决尺规作图这类问题，首先要想象出符合要求的图形，在此基础上展开几何逆向推理，进行有关联想，获得目标图形，然后利用基本的尺规作图，作出目标图形.

作法探寻

1. 作图原理——直径所对的圆周角是直角

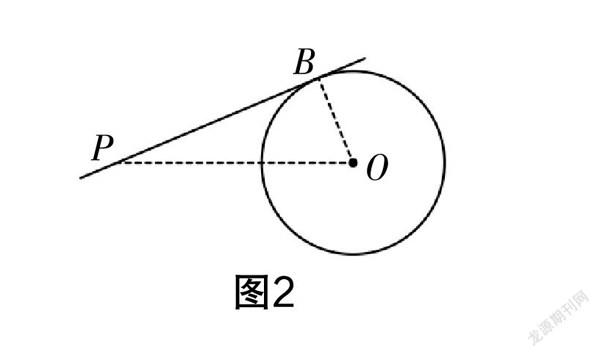
首先需要画出符合要求的图形，进行可能的几何构图. 如图2，假设过点P已经画出PB是☉O的切线，根据切线的性质，我们能得到PB⊥OB. △PBO是Rt△，并且点P和点O确定，现在要确定点B，点B是直角顶点，学生会想到什么？很自然地，学生会联想到直径所对的圆周角是直角，这个目标图形就是直径PO所对的圆周角.

作法：如图3，作PO的垂直平分线，找到PO的中点A，然后以A为圆心，AP或AO为半径作☉A，交☉O于点B，则直线PB就是☉O的切线.

2. 作图原理——同弧所对的圆周角相等

如图4，假设过点P已经画出PB是☉O的切线，根据切线的性质，得到PB⊥OB，△PBO是Rt△. 如果我们根据同弧所对的圆周角相等，构造一个△PCO，使PC⊥OC，这样只要作Rt△PCO的外接圆☉A，☉A与☉O的交点为点B，则∠PBO=∠PCO=90°，又因为PB经过☉O的外端点B，所以PB是☉O的切线，目标图形就是直角∠PCO.

作法：如图5，作射线PE，过直线外一点O作OC⊥PE，垂足为C，作△PCO的外接圆，交☉O与点B，作直线PB，则直线PB就是☉O的切线.

3. 作图原理——一边上的中线等于这条边的一半的三角形是直角三角形

除了直径所对的圆周角是直角，同弧所对的圆周角相等外，还能如何判断△PBO是Rt△呢？学生会联想到在一个三角形中，如果一条边上的中线等于这条边的一半，那么这个三角形也是直角三角形，目标图形就是中线BC（满足BC=1/2PO）.

如图6，学生只需要找到PO的中点C，然后以C为圆心，CO为半径画弧，交☉O于点B，则直线PB就是☉O的切线.

作法：如图7，作PO的垂直平分线，找到PO的中点C，或者为了和作法1不同，也可以在☉O上任选一点A，连接OA，PA. 作OA的垂直平分线，找到OA的中点D，作∠OAP=∠ODC. 交PO于点C，以C为圆心，CO为半径画弧，交☉O于点D，则直线PB就是☉O的切线.

4. 作图原理——全等三角形对应角相等

由于确定点B存在困难， 不妨先构造一个与其全等的Rt△DAO，使得半径OA=OB，OD=OP，DA=PB. 由于∠DAO为90°，所以∠PBO为90°，又因为PB经过点B，所以，直线PB就是☉O的切线. 所以目标图形就是Rt△DAO.

作法：如图8，在圆上任意选一个点A（不与点B重合），连接OA，过点A作OA的垂线AC，以点O为圆心，OP为半径画弧，交直线AC与点D，连接OD，得到Rt△DAO，显然直线DA是☉O的切线，以P为圆心，DA为半径画弧，交☉O于点B，则直线PB就是☉O的切线.

5. 作图原理——等腰三角形三线合一

由于切线垂直过切点的半径，不妨构造目标图形——等腰△POC. 根据等腰三角形三线合一，能得到直线PB是☉O的切线，所以目标图形就是等腰△POC.

作法：如图9，在圆上任意取一点A，延长OA并截取，使得OA=AD，以O为圆心，OD为半径画大圆O，再以点P为圆心，OP为半径画弧，交大圆O于点C，连接OC，OP，PC，则得到目标图形——等腰△POC. 因为OC与小圆O交于点B，则OB=BC，连接PB，根据等腰三角形的三线合一，得到直线PB是☉O的切线.

6. 作图原理——射影定理和切割线定理

如图10，画好切线PB，割线PA交☉O于点D，根据切割线定理，得到PB2=PD·PA，联想到母子三角形相似时，根据射影定理，得到PE2=PD·PA，那么PB=PE，要想作出切线PB，只要得到PE即可，所以目标图形就是线段PE.

作法：如图11，连接PO，并延长，交☉O于点D和点A，作PA的中点C，以点C为圆心，CP为半径画半圆，过点D作DE⊥PA，交半圆于点E，连接PE和AE. 这样根据射影定理，得PE2=PD·PA，然后，以点P为圆心，PE为半径画弧，交☉O于点B，連接PB，则直线PB是☉O的切线.3B07C8FC-B918-4C58-BC2A-B1B86894886D

教学启示

1. 关注课程标准，培养作图能力[2]

课标要求：（1）能用尺规完成以下基本作图：作一条线段等于已知线段;作一个角等于已知角;作一个角的角平分线;作一条线段的垂直平分线;过一点作已知直线的垂线. （2）会利用基本作图作三角形：已知三边、两边及其夹角、两角及其夹边作三角形;已知底边及底边上的高线作等腰三角形;已知一直角边和斜边作直角三角形. （3）会利用基本作图完成：过不在同一直线上的三点作圆，作三角形的外接圆、内切圆;作圆的内接正方形和正六边形. （4）在尺规作图中，了解作图的道理，保留作图的痕迹，不要求写出作法.

由于教材中没有把尺规作图作为独立的一章来归纳和总结，只是把与尺规作图有关的知识零星分布在不同的章节，导致一些教师教学时对尺规作图不太关注. 遇到尺规作图的问题，把其当成技能来训练，忽略对其背后的作图本质和作图的原理的思考. 在日常教学中，因为平时作业中很少尺规作图，平时考试也几乎不考作图，导致部分教师没有把尺规作图放在一个重要的位置，忽视了尺规作图的重要性，使得学生对尺规作图题不会分析，找不到作图的本质，不明白作图的原理，缺乏系统的认识. 因此，笔者借这次南京市中考数学尺规作图题，引导教师关注课标，重视尺规作图，培养学生尺规作图的能力.

2. 深入分析条件，探寻作图本质

尺规作图需要学生先分析条件，这道题 “已知什么，要作什么”，然后再思考该怎么作？已知圆外一点P和☉O，要过点P作☉O的切线. 下面该怎么作呢？在☉O上找点B，使得直线PB是☉O的切线. 怎么找点B，进行可能的几何构图，在构图直观的基础上展开几何逆向推理，并作出判断，获得目标图形，作出目标图形.

在平时的教学中，应引导学生以分析条件为重点，要求学生对题中的条件要逐个地去思考，依據定义、公理或定理等，把已知条件进行一步步推理，得出新的结论，由果索因，延伸出尽可能多的结论，贯通条件和结论的“桥梁”. 同时分析问题的过程中也不要忽视题中的隐含条件，比如本题中☉O的半径和OP的长是已知的. 这道尺规作图题，找到目标图形是直角三角形后，学生接着就要思考，如何才能确定直角顶点，如何作出目标图形，学生自然会和数学知识建立关联，想到直径所对的圆周角是直角，如果一个三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形，等腰三角形的三线合一等，这些就是学生需要探寻的作图原理.

3. 经历作图过程，明晰作法之理

教师在日常教学中，应该让学生经历完整的尺规作图的思考过程，不仅要求学生会尺规作图，还要求学生明白尺规作图的道理. 笔者曾经问过一个九年级的学生，作一个三角形的外接圆该怎么作？这个学生不假思索地告诉笔者：“作这个三角形两条边的垂直平分线，其交点就是圆心，这个交点与其中一个顶点的连线就是半径. ”笔者接着追问：“为什么要作垂直平分线呢？”他的回答出乎笔者的意料，他说：“老师就是这样教的. ”可见，学生并不清楚这样作图的道理，作一个三角形的外接圆为什么要作这个三角形两条边的垂直平分线，其实作三角形的外接圆是根据到线段两端的距离相等的点在这条线段的垂直平分线上，这才是“作法之理”.

在平时的教学中，教师要关注学生这种尺规作图的方法是“怎么想到的”，要对学生适时进行引导，让学生亲自去分析条件，去体验，去动手操作，去经历探索作法的过程，明晰作图的道理. 学生只有亲历这个过程，才能对尺规作图问题积累更加丰富的作图经验.

4. 发散学生思维，领悟多种作法[3]

根据五种基本的尺规作图，能产生很多综合性的方法，这个探究的过程就是学生数学思维的发散. 本题要求用两种不同的方法作图，并对每一种方法给出文字说明，在学生知法明理的基础上，融入逻辑推理，让学生在动手、动脑、动口中发散数学思维.

在教学过程中，教师要引领学生从不同的方向和角度去深入探究，找到此题尺规作图问题的不同作法，领悟到数学的魅力和乐趣. 只有学生认真去研究一个问题，深入地思考下去，主动去分析，才能逐渐领悟出其中的道理. 同时对一道尺规作图题进行深刻的剖析，可以优化作图的方法，训练学生思维的发散性，建立与该几何知识点相关的知识链，使得学生对几何的学习形成一个系统的结构，提升学生的数学核心素养.

在平时的课堂教学中，教师要不断优化自己的教学设计，多从学生的角度去考虑，对尺规作图的教学课可以设计一些开放性问题，以解放学生的思维，促进学生思维的发展. 问题的设计，需让学生先独立思考，然后互相交流，这样学生能积极投入思考中，通过变换不同的思维方式，明晰作图之理，学会尺规作图. 同时，问题的设计也能发散学生的数学思维，激发学生的创新意识，促使学生领悟多种作法.

参考文献：

[1]顾香才. 归纳来“推断”，演绎去“验证”——在“尺规作图”教学中领悟波利亚的解题思想[J]. 中学数学，2021（04）：21-22+25.

[2]中华人民共和国教育部. 义务教育数学课程标准（2022年版）[M]. 北京：北京师范大学出版社，2022.

[3]肖世兵. 近三年中考“ 尺规作图”命题分析、感悟及实践[J]. 中学数学杂志，2020（06）：60-62.3B07C8FC-B918-4C58-BC2A-B1B86894886D