异步电机转速估计方法及仿真研究

于宗艳，韩连涛，王 丽

（1.黑龙江科技大学 电气与控制工程学院，哈尔滨 150022；2.哈电发电设备国家工程研究中心有限公司，哈尔滨 150040）

在异步电机的控制中，为了达到高精度的转速闭环控制，需要对异步电机的转速进行检测。 另外，为了合理匹配电机系统，也需要对电机系统的实际转速进行监测，从而根据电机系统的实际运行状态选择电机。 由此可见，在异步电机的使用和控制中，对转速的检测是十分重要的。 对于转速的检测可以采用旋转编码器等速度传感器，但是这种方法存在如下问题：这些传感器价格昂贵；传感器的安装十分困难，甚至无法安装；在恶劣环境或安装不当将影响检测精度。 所以采用传感器检测速度的方法不但增加了成本，而且还会降低电机系统的机械强度和鲁棒性。 为了解决上述问题，开始研究无速度传感器测量技术，并取得了大量的成果。

无速度传感器转速估计方法主要有电机模型直接计算法、扩展卡尔曼滤波器算法[1]、神经网络法[2-3]、高频信号注入法[4]、滑膜观测器法[5]和模型参考自适应法[6]等。 但电机模型直接算法不能随异步电机参数的变化而实时地计算出转速；扩展卡尔曼滤波器是一种对非线性系统的随机观测器，运用最小方差最优预测估计法来削弱随机干扰和测量噪声。 其算法复杂、计算量大，运算费时；神经网络法广泛用于模式识别、系统辨识和估计等场合。 但其结构和权值不具有定性的物理意义，系统易陷入局部最优；高频信号注入法和电机实体有关，缺乏普遍性；滑膜观测器因其固有的变结构特性，使该方法对电机模型的精确程度依赖更低[7-8]。 但滑膜观测器法存在系统抖振问题，另外，能够保证系统在不同工况下的稳定性问题，也是滑膜观测器需要解决的问题。 为了解决系统稳定性和抖振问题，研究者们对滑膜观测器进行了许多改进，但改进后的方法增加了系统设计的复杂性，进而限制了其实际应用范围。

文献[9]提出了基于转子磁链的模型参考自适应方法，利用测得的端电压和电流来估计电机转速。模型参考自适应（MRAS）方法由于算法简单、稳态精度较高已被广泛应用于电机的控制[10-11]。 本文将使用MRAS 法来估计异步电机的转速。

1 模型参考自适应算法

MRAS 基本结构如图1 所示[12]，参考模型和可调模型被相同的外部输入所激励，x 和分别是参考模型和可调模型的状态矢量。 参考模型用其状态x（或输出）规定了一个给定的性能指标，这个性能指标与测得的可调模型的性能比较后， 将其差值矢量v 输入自适应机构，由自适应机构来修改可调模型的参数， 使得可调模型的状态能够快速而稳定地逼近x，也就是使差值v 趋近于零。

图1 MRAS 基本结构Fig.1 Basic structure of MRAS

本文在构造MRAS 对异步电机的转速进行估计时所使用的参考模型和可调模型如式（1）和式（2）所示。 将式（1）和式（2）表示成静止DQ 坐标系下的分量形式如式（3）和式（4）所示。

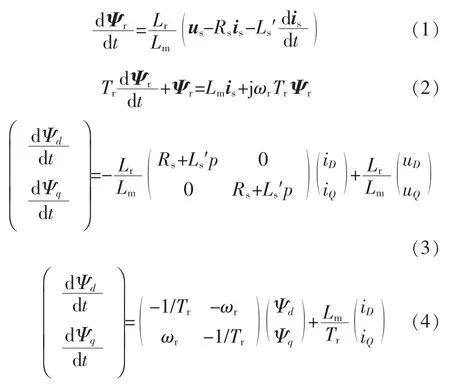
式中：Ψr为转子磁链；Rs为定子电阻；Ls为定子等效自感；Lr为转子等效自感；Lm为定、转子等效励磁电感为定子瞬态电感为转子时间常数；us为定子电压；is为定子电流；ωr为转子速度。

将ωr作为可调参数，记为如果由可调模型估计的转子磁链矢量与参考模型确定的Ψr相同，那么转速估计值一定与实际值ωr一致；如果两者存在偏差，说明估计值与实际值ωr不符。由此可见， 转速估计偏差与两个模型估计的转子磁链矢量误差间一定有必然的联系，图1 中的自适应机构，就是利用这个转子磁链矢量误差构建一个合适的自适应律，使得可调模型的能逼近真实的ωr。

下面设计自适应律。 因为MRAS 自身就是一个时变的非线性系统，其稳定性是首要解决的问题，所以本文采用波波夫稳定性理论来设计自适应律。 得到的自适应律如式（5）所示。

可得图2 所示的用于异步电机转速估计的MRAS 模型。

图2 自适应律Fig.2 Adaptive control law

2 仿真分析

在仿真中，交流异步电机的参数分别取：额定功率PN=2.2 kW；额定电压UN=380 V；额定频率fN=50 Hz；定子电阻Rs=0.435 Ω；定子漏电感Lσs=0.002 H；转子电阻Rr=0.816 Ω；转子漏电感Lσr=0.002 H；互感Lm=0.069 H；转动惯量J=0.18 kg·m2；摩擦因子F=0.1 N·m；极对数p=2。

根据前文介绍的基于MRAS 的异步电机转速估计方法搭建的异步电机转速估计及矢量控制Simulink 仿真模型如图3 所示，包括异步电机模块、逆变器模块、电流滞环控制器模块、转速估计模块、坐标变换模块、转子磁链观测模块及转速控制器模块（ASR）、转矩控制器模块（ATR）和磁链控制器模块（ApsiR）。 其中，ASR、ATR 和ApsiR 均采用的是PI 控制规律。 转速估计模块的内部组成如图4所示。

图3 Simulink 仿真模型Fig.3 Simulation model of Simulink

图4 MRAS 转速估计模块结构Fig.4 Structure of MRAS speed estimating model

异步电机矢量控制采用的基于转子磁场定向的矢量控制， 而转子磁场定向采用的是由MT 轴系给出的电流-转速模型。 异步电机矢量控制方程为

式中：Te和ωf分别为电磁转矩和转差频率；iM和iT分别为定子电流的励磁分量和转矩分量；θM为转子磁链角。

仿真参数设置情况：仿真算法为ode45，仿真时间为1 s，电动机空载启动，设定转速为1000 r/min，在t=0.6 s 时加载使负载转矩TL=55 N·m。

图5 所示为异步电机在起动和加载过程中估计转速和实际转速的波形对比。 从图5 波形中可以看到，电机刚启动时二者略有差异，但很快估计转速就能够跟踪上实际转速，且与实际转速差异很小。

图5 异步电机估计转速与实际转速Fig.5 Estimating speed and actual speed of induction motor

图6～图7 为利用MRAS 估计的转速进行异步电机矢量控制在电机起动和加载过程中电动机转矩和定子电流的变化过程，从图中可以看出估计转速矢量控制系统可以取得与测量转速矢量控制系统几乎相同的控制效果。

图6 异步电机电磁转矩Fig.6 Electromagnetic toque of induction motor

图7 异步电机定子三相电流Fig.7 Stator current of induction motor

3 结语

针对采用传感器检测速度存在的增加成本、降低系统的机械强度和鲁棒性等问题，在对比了多种无速度传感器检测方法后， 本文采用了基于MRAS的无速度传感器检测方法来估计异步电机的转速。利用Simulink 搭建了基于MRAS 的异步电机转速估计及矢量控制系统并进行了仿真实验。 结果表明该方法能够实时地估计异步电机的转速， 基于MRAS 转速估计方法构造的异步电机矢量控制系统，具有良好的动、静态性能，取得了较好的控制效果。

基于MRAS 转速估计的关键问题是自适应律的PI 参数确定问题。 经过反复调整，当Kp=50000，Ki=10 时转速估计的效果最佳。

通过仿真实验可以看出MRAS 转速估计方法在低速时存在估计转速与实际转速有差异的问题。

下一步的工作是对本文讨论的MRAS 转速估计方法进行改进，使其在全速范围内都能够对转速进行准确的估计。