基于改进PSO-PID算法的液压机压下系统控制优化

苏 力，薛 峰

（1.西安航空学院 电子工程学院，西安 710077；2.西北工业大学 电子信息学院，西安 710072）

采用双辊薄带铸轧工艺可以实现钢液的快速凝固过程，从而获得更高的钢铁材料生产效率[1-4]。文献[5]在传统铸轧方法基础上实施了进一步优化，设计了一种可以实现双辊薄带振动铸轧的新工艺，当振动辊发生振动时，从而显著降低裂纹缺陷并控制偏析程度， 并促进板带中形成更加细小的晶粒，制备得到综合性能更优的板带。 但考虑到传统铸轧通常都是在较恶劣的环境中进行，会受到多种外部影响， 尤其是轧辊辊缝会受到轧制力的明显干扰，从而无法精确控制铸轧得到的板带纵向厚度[6-7]。 相对于传统铸轧方式，双辊薄带振动铸轧采用的轧制工艺存在一定的差异，当振动铸轧辊方式上下运动的时候会导致Kiss 点出现不稳定波动的情况，从而在轧制期间发生轧制力的大幅波动，因此与传统铸轧相比振动铸轧的辊缝控制难度更大，无法达到理想的精度[8-10]。 铸轧属于板带加工的第一道工序，使成品板带的纵向上出现明显的厚度差异，引起成品板带质量不达标的问题，因此需有效克服铸轧阶段存在的板带纵向厚度误差大的缺陷[11-12]。

为尽量减少优化过程的迭代次数并达到更高的求解精度，本文综合运用粒子群收缩因子算法与扰动因子构建得到PSO 算法。该算法处理过程较简单，只需对少数参数进行调控，可以实现快速收敛的过程，同时获得精度很高的最优解。 为了对本文算法优越性进行验证， 完成测试函数的仿真分析。为确认此优化算法对双辊薄带振动铸轧工艺的适用性，利用AMESim 与Matlab 联合仿真的方式对其实施验证。

1 本文算法

本文设计了一种由带极值扰动实现的粒子群收敛因子算法，即PSO 算法，可以将其表述成以下数学过程：先对一群粒子实施初始化，粒子寻优存在一个潜在最优解；通过位置、适应度、速度各个参数来作为粒子状态的分析依据，各粒子都有相应的适应度值，可以根据该值判断粒子优劣性[13-14]。

对于m 维空间， 存在由n 个粒子构成的种群，将其表示为X， 各粒子分别对应一个m 维向量Xi，表示m 维搜索空间内第i 个粒子所处的位置。 再利用目标函数计算得到各粒子位置Xi适应度值。Vi表示第i 个粒子运行速度，以Pi表示个体的极值，群体极值为Pg，则存在以下关系式：

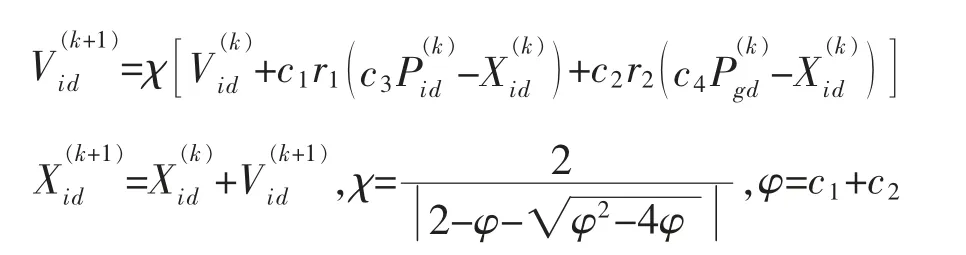
式中：k 表示目前迭代的总次数；χ 表示收缩因子；c1，c2是学习因子，通常取c1=c2=21.05；V（k）表示粒子速度；X（k）表示粒子位置；c3，c4是扰动因子；r1，r2是随机函数U （0，1）；T0，Tg依次表示个体极值与全局极值扰动时的停滞步数阈值，通常将其设定在3；t0，tg分表示个体与全局极值进化停滞的步数。

2 控制优化

通过AMESim 构建得到压下系统的运行控制模型，并利用Matlab 软件建立了PSO-PID 算法的流程，以Visualstudio 完成软件之间的数据传输[15]。 振动铸轧压状态下的各项系统模型参数如表1 所示。

表1 液压机压下系统物理模型参数Tab.1 Physical model parameters of the system under pressure of hydraulic press

进行仿真测试时，11.5 s 时设置了一个干扰力F来模拟轧制阶段受到轧制力因素的影响。以PSO 算法并结合误差积分计算过程优化了PID 控制器的Kp与Ki。本文以时间与绝对误差相乘进行积分的结果来判断粒子群优化PID 参数适应度。 进行振动铸轧的时候，轧制力形成了周期较短但幅度很大的波动性，要求液压压下系统可以实现高效瞬态响应以避免轧制力波动而引起辊缝产生较大冲击的情况。

仿真时液压机压下系统控制结构如图1 所示。

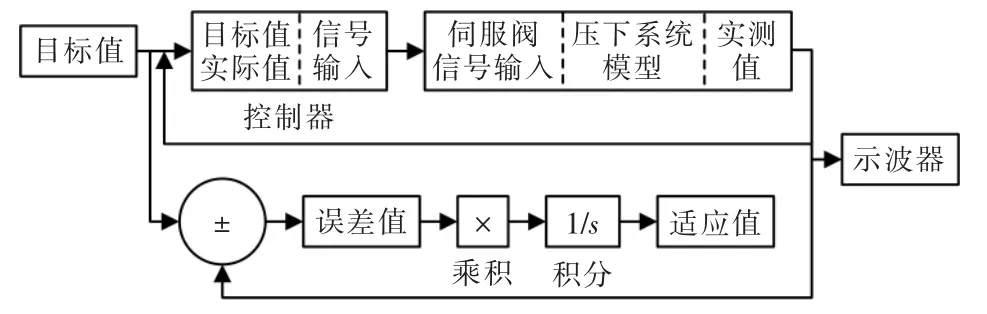
图1 液压机压下控制系统结构图Fig.1 Hydraulic press down control system structure diagram

以粒子群算法对控制系统参数进行优化的流程如图2 所示。 误差目标函数对PSO-PID 控制器进行迭代计算100 次得到的优化参数结果，如图3 所示。 分析图3 发现，迭代到50 次时便获得了理想的控制参数，实现了系统性能的显著提升。

图2 粒子群优化PID 参数流程Fig.2 PID parameter flow chart of particle swarm optimization

图3 参数优化Fig.3 Parameter optimization

抗干扰能力结果如图4 所示，上述方法进行整定得到的PID 参数如表2 所示。 根据图4 可知，对系统施加干扰作用后，普通PID 控制方式下的辊缝振荡幅度达到了01.1 mm，当以PSO-PID 控制时振荡幅度只有01.05 mm，实现了抗干扰能力的显著提升，显著改善了板带纵向厚度误差。

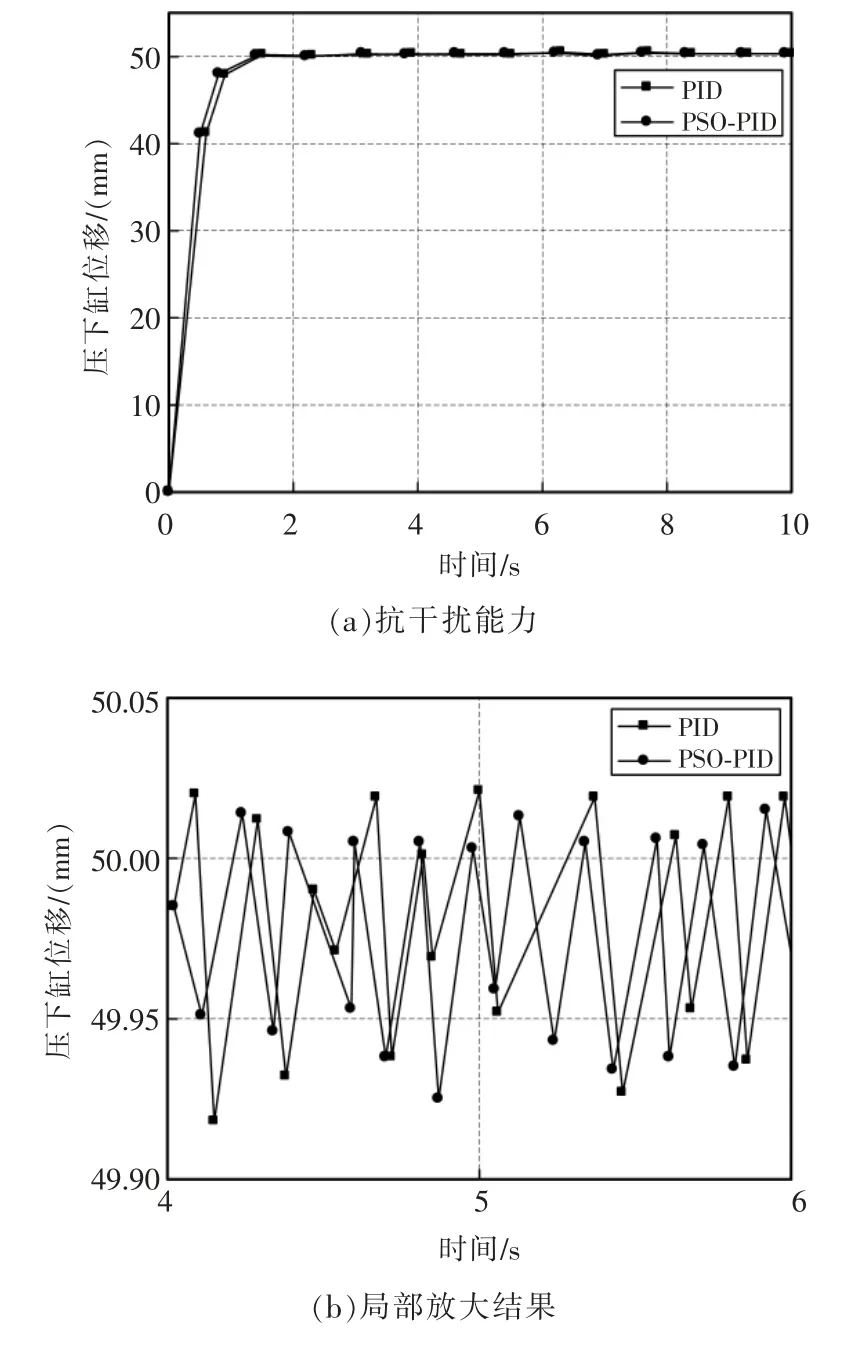
图4 抗干扰能力及局部放大结果Fig.4 Anti-interference capability and local amplification results

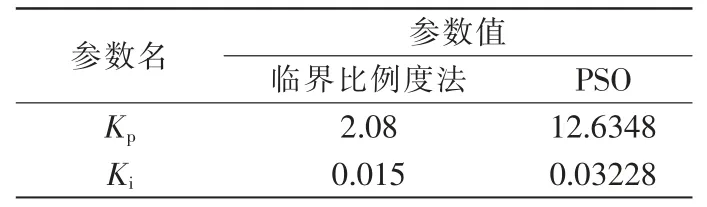
表2 整定参数值Tab.2 Setting parameter values

3 试验验证

为了对PSO-PID 实用性进行验证，把采集获得的辊缝宽度参数通过PID 和PSO-PID 进行抗干扰性能比较，得到的辊缝宽度误差测试结果如图5 所示。

根据图5 可知，采用PSO-PID 方法得到的辊缝宽度误差等于1.1 mm，以PID 方法得到的辊缝宽度误差等于1.2 mm。 以上测试结果显示，PSO-PID 可以获得更优的控制效果，能够更精确控制板带纵向厚度误差。 并且进行振动铸轧时，轧制力发生波动也会引起液压压下系统发生响应，由此实现降低轧制力波动性的作用， 其中，Kiss 点升高的过程中，轧制力逐渐增大，同时形成了更大的辊缝宽度，引起Kiss 点位置发生下降现象。 而辊缝宽度需控制在合理的变化范围内，当形成太宽的辊缝时会引起板带厚度产生明显的纵向误差。 采用本文PSO-PID 控制器进行控制时，能够降低板带纵向厚度误差。

图5 辊缝宽度误差对比Fig.5 Error comparison of roll gap width

4 结语

通过对比PSO 算法和其它各算法可以发现，此算法相对其它粒子群优化算法可以获得更快求解速度并提升了控制精度。 并且由于此算法实现过程简单，为实现双辊薄带振动铸轧工业化应用提供了理论参考。 设计了PSO-PID 优化方法来控制轧制力发生明显周期性波动的情况，由此实现精确的压下控制，降低了轧制力的波动程度，由此实现精确控制辊缝宽度的效果。