基于递归神经网络的全海深载人潜水器控制分配研究

邓 超，赵 洋，赵 兵，陈帅华

（1.中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳 110016；2.中国科学院机器人与智能制造创新研究院，沈阳 110169；3.辽宁省水下机器人重点实验室，沈阳 110169；4.中国科学院大学，北京 100049）

2020年，我国首艘全海深载人潜水器“奋斗者”号成功下潜至马里亚纳海沟10909 m 海底，标志着我国具有了进入海洋最深处开展科学研究的能力。控制系统是载人潜水器的“大脑和中枢神经”，负责对载人潜水器进行运动控制。 “奋斗者”号的运动控制主要有速度控制和位姿控制2 种模式，分别如图1 和图2 所示，2 种控制模式都有控制分配计算模块。 为了使载人潜水器具有良好的机动性能和容错性能，其推进器的数量大于载人潜水器的运动自由度。 对于这样的冗余控制系统，给定控制量，执行器的输出解不唯一[1]。 而控制分配的目的就是在控制器或操纵杆输出期望推力后，在某种优化规则下，为每一个推进器分配一个推力，使所有推进器合力尽可能满足期望推力。 此外控制分配还要考虑2 个约束：一是推进器所能提供的最大推力，即推进器的饱和约束；二是为了保护电机而采取的推进器变化率的约束。

图1 载人潜水器速度控制系统框图Fig.1 Diagram of manned submersible speed control system

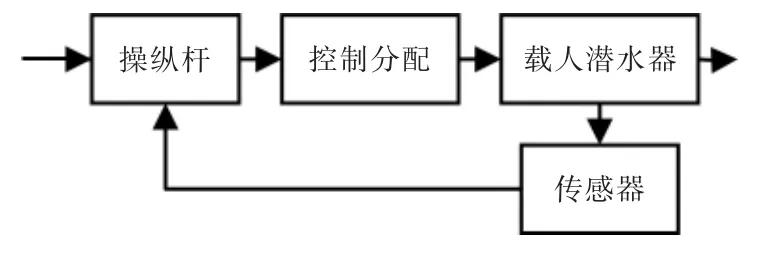
图2 载人潜水器位姿控制系统框图Fig.2 Diagram of manned submersible position control system

控制分配广泛存在于航空[2-3]、汽车[4]、船舶[5]和水下航行器[6-7]等领域。 文献[8]将控制分配问题分为无约束控制分配问题和有约束控制分配问题。 载人潜水器的推进器存在工作区间，因此载人潜水器的控制分配问题是典型的有约束控制分配问题。 针对有约束控制问题，文献[9]提出一种将控制量归一化再与伪逆相结合的方法， 解决了推进器饱和的问题，但固定的分配方法可以解出可行解，却不是最优解；文献[10]针对控制分配中的优化问题提出了人工蜂群算法，然而人工蜂群算法等智能算法计算优化问题所需的时间取决于优化问题的维度和结构，往往很难满足实时性要求[11]。

为了提高控制分配问题的计算速度与效率，本文利用递归神经网络解决控制分配问题中的优化问题，并将递归神经网络配置在FPGA 上，通过仿真验证了递归神经网络的有效性和实时计算的可行性。

1 控制分配问题描述

1.1 载人潜水器推进系统建模

以“奋斗者”号的重心为原点建立坐标系o-xyz，ox 指向“奋斗者”的正前方，oy 指向右舷，oz 指向底部。 “奋斗者”配备有9 个推进器，其分布如图3 所示。 艉部布置4 个推进器，为“奋斗者”提供进退和转向所需的推力，靠近底部的2 个推进器呈矢量分布，与x 轴夹角为α，另外2 个艉部推进器水平布置。舯部布置4 个垂向推进器，提供上浮下潜和纵倾所需的推力。 艏部布置1 个侧向推进器，提供侧移和转向所需的推力。

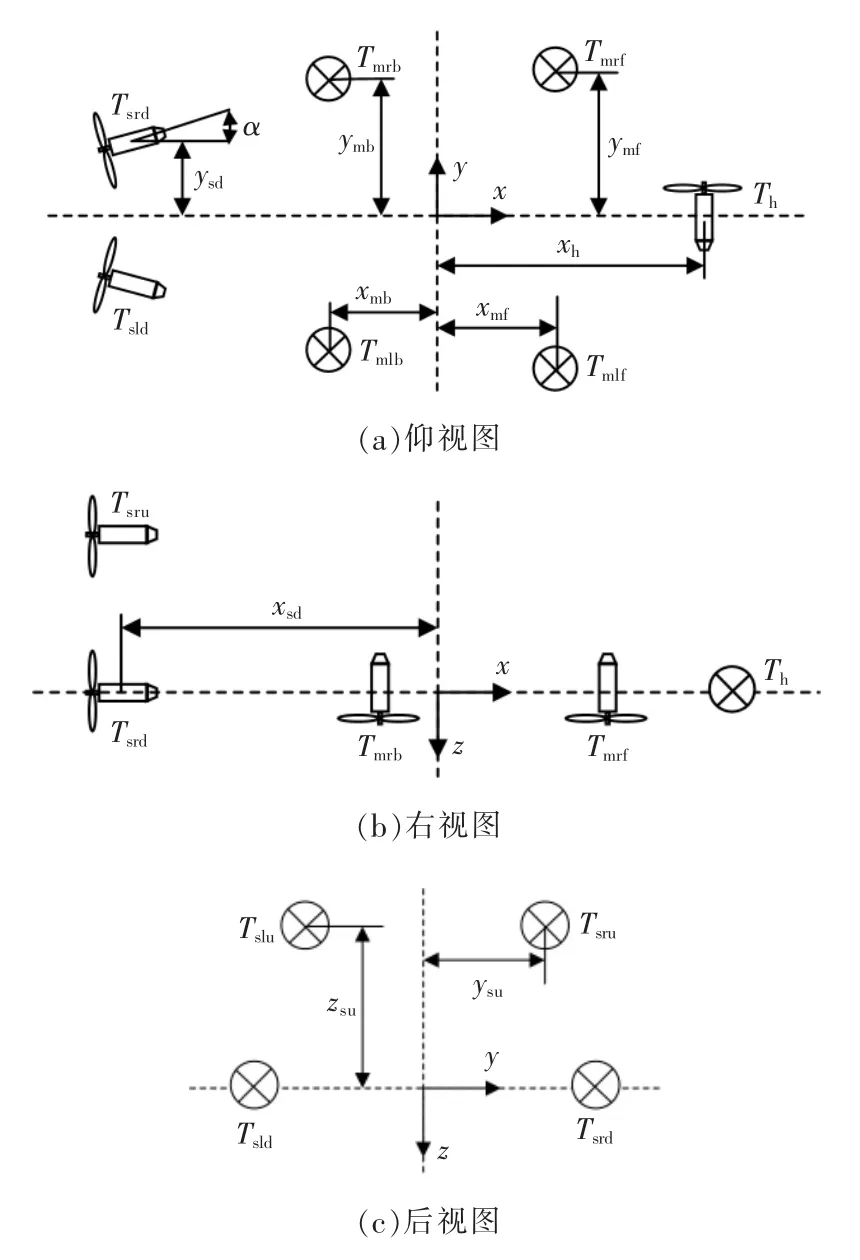
图3 “奋斗者”推进器分布示意图Fig.3 Distribution of “Fendouzhe” thrusters

为了方便研究，文献[12]对推进器模型做出如下假设：①忽略推进器的控制环动力学；②忽略推进器产生的扭矩；③忽略环境水流速度对推力的影响；④推进器正反向具有相同的推力特性。 本文仍按上述假设开展算法研究。

六自由度期望推力定义为

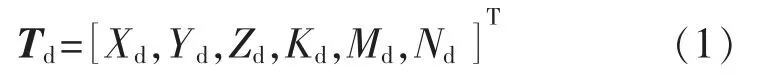
各推进器推力定义为

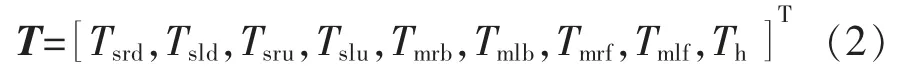
推进器的六自由度合力定义为

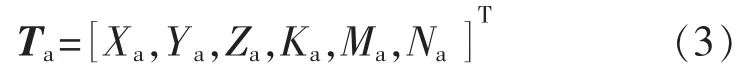
跟据图3 的推进器的布置示意图，控制分配矩阵B 表示为

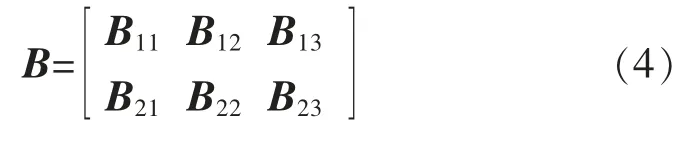
其中控制分配矩阵B 的各个子块可表示如下：

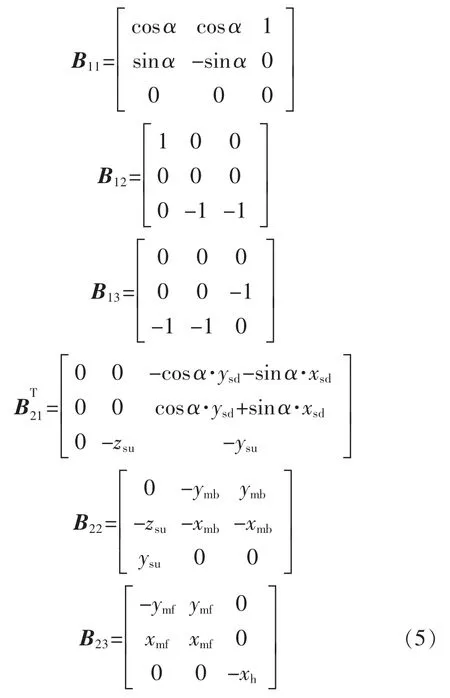
显然有：

1.2 递归神经网络

随着人工智能的发展，递归神经网络也在快速的发展和普及。 由于其具有并行计算和易于硬件实现的优点，递归神经网络可用于处理具有实时性要求和计算量大的优化问题[13]。 Tank 和Hopfield 首次提出了求解线性优化问题的递归神经网络。 此后，研究人员针对二次规划、凸优化和非凸优化等优化问题提出了多种递归神经网络[14-16]。 因此本文采用递归神经网络解决控制分配中的优化问题。

2 控制分配策略

控制分配的代价函数定义为

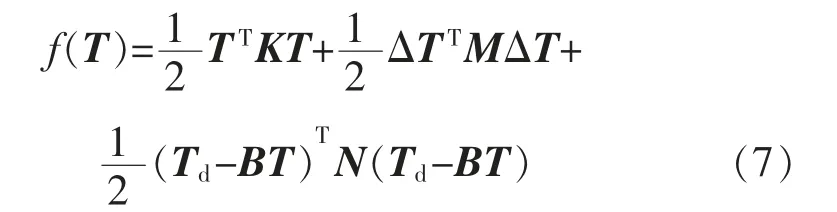
约束条件为

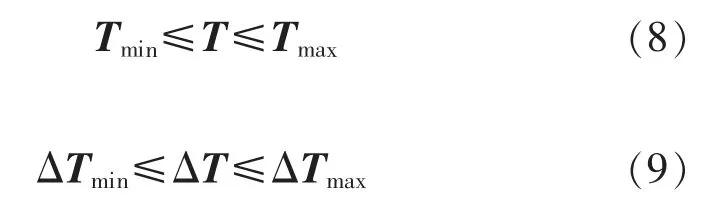
式中：K、M 和N 为非负定对角矩阵；ΔT 是推力的变化率，其计算方法为

T0是上一采样时刻推进器推力；代价函数等号右边的第一项是推力的二次优化项；第二项是推进器变化率的惩罚项；第三项是期望推力与实际推力的误差惩罚项，为了使实际推力尽可能的与期望推力相等；当期望推力超出约束范围时，惩罚项的作用是找到在约束条件下最接近期望推力的解。

结合式（8）～式（10），将问题转化为如下凸优化问题：

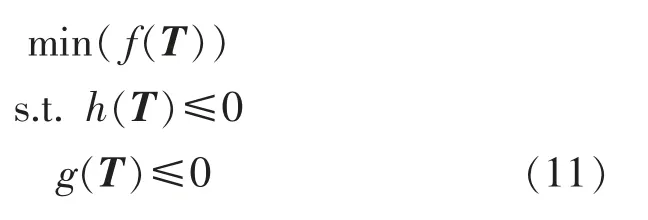
其中：

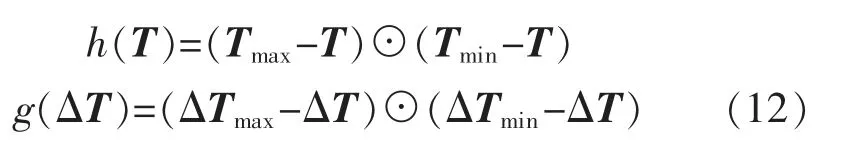
结合式（10），上式可以写为

式中：⊙为向量元素乘积；h（T）和g（T）是向量函数，且每个元素均小于0；f（T），h（T）和g（T）均是凸函数且二次连续可微。

上述凸优化问题的Lagrange 函数可以写为[17]

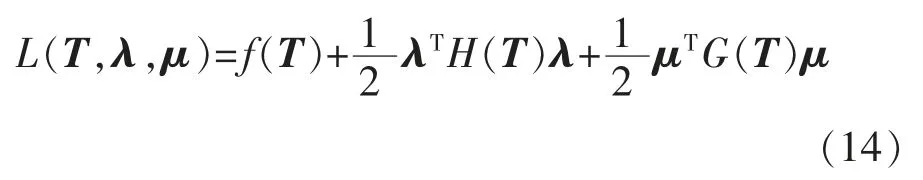
式中：H（T）=diag［h（T））］，G（T）=diag［g（T））］；λ 和μ 为乘子矩阵且矩阵内所有元素均大于0。 对于问题，显然至少存在一个T 满足：

即满足Slater 条件，因此下式为凸优化问题最优解的充要条件：

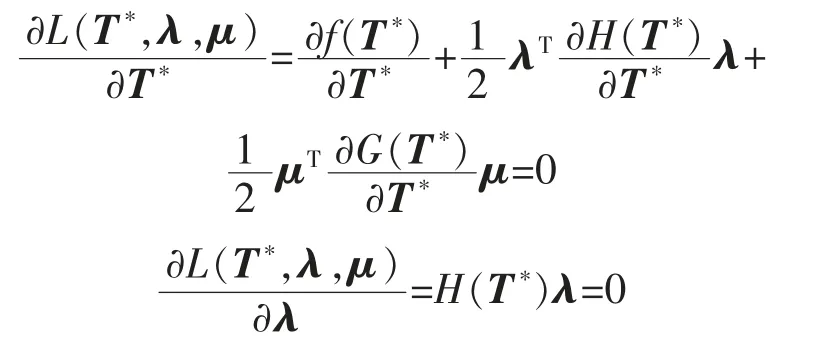
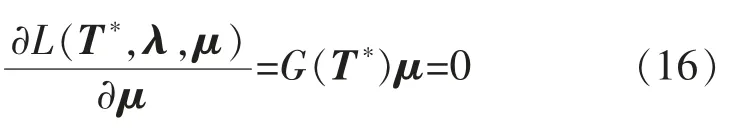
令神经网络的状态为

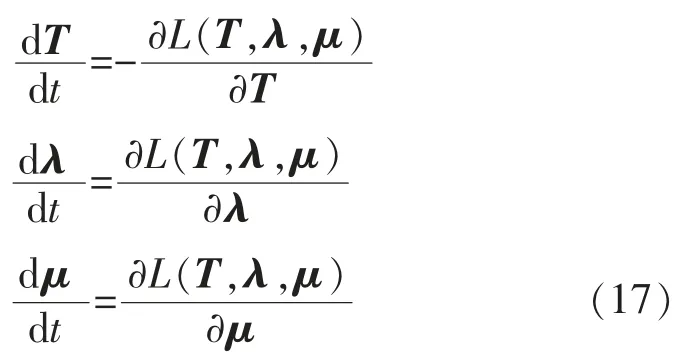
神经网络中的神经元λ 和μ 将稳态点控制在约束范围内，神经元T 使Lagrange 函数不断减小。当神经网络达到稳态时：

即为代价函数的全局最优解[18]。 图4 为基于神经网络的控制分配图，当控制系统输入六自由度期望推力Td时，控制分配系统开始工作，最终计算出优化解T。

图4 神经网络控制分配结构图Fig.4 Diagram of the neural network for control allocation

3 仿真结果

仿真开始时，令T=0，λ=I，μ=I，矩阵K、M 和N设为单位矩阵。 推进器饱和约束设为±1 kN，推进器变化率约束设为±0.1 kN。仿真采取图1 所示的控制模式，根据图4 搭建的递归神经网络Simulink 模型如图5 所示。

图5 的Simulink 模型输入1 是六自由度期望推力Td，输入2 是上一时刻推力T0，输出是经过神经网络计算的各推进器推力T。运行该神经网络，推力T 的计算结果如图6 所示。 可以看出，推进器推力在仿真时间的第1 s 就已经收敛。 但初始值不同，神经网络的收敛时间也不同，为了保证计算结果充分收敛，选5 s 作为一个计算周期。

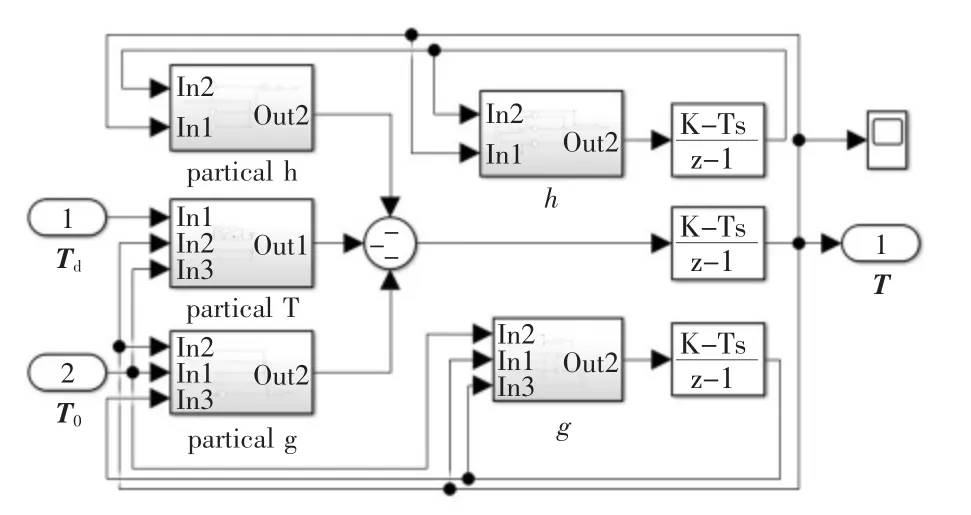
图5 递归神经网络Simulink 模型Fig.5 Simulink model of recurrent neural network

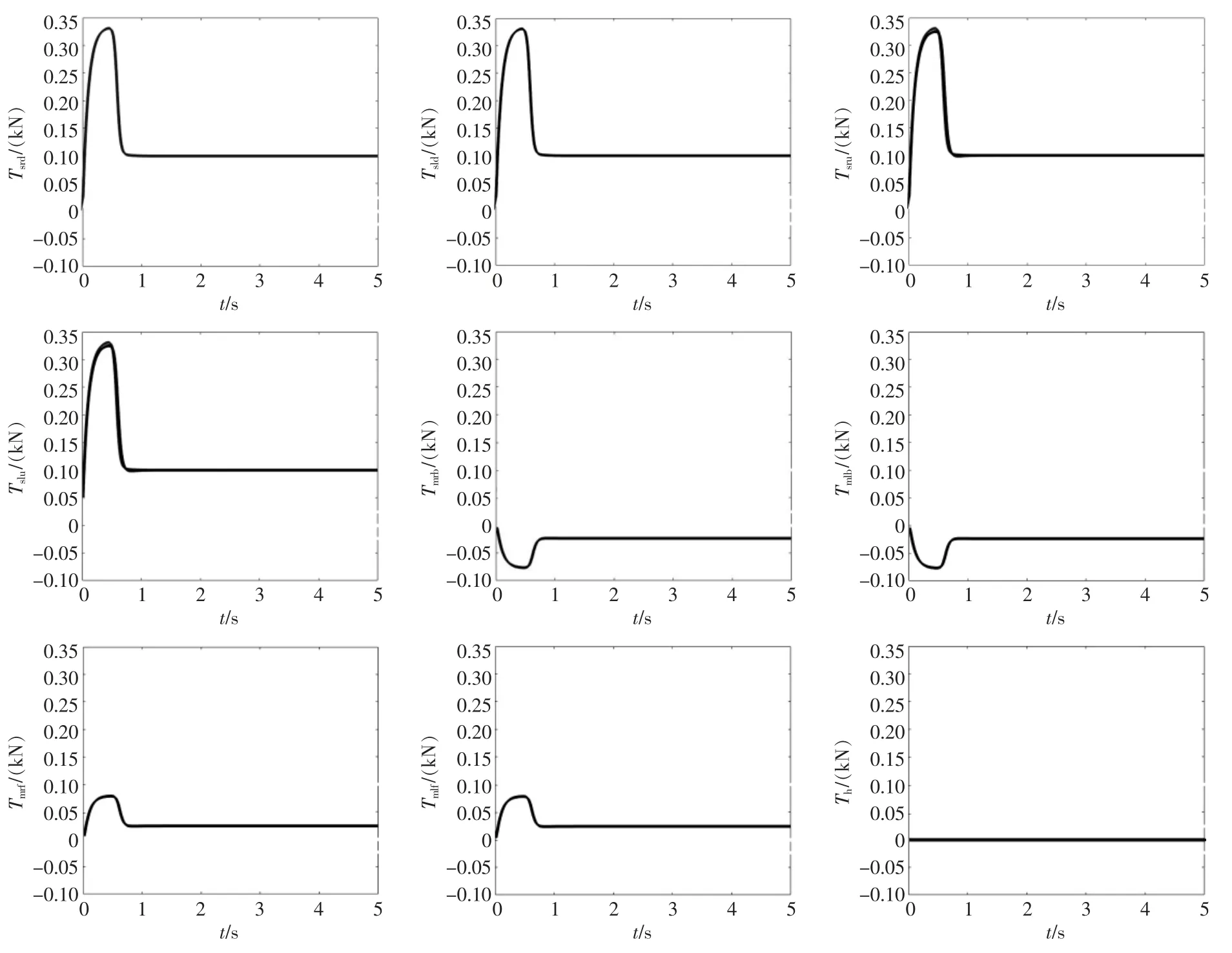
图6 推力计算曲线Fig.6 Thrust calculation curve

Simulink 的仿真模型如图7 所示。 图7 中的输入为6 维阶跃信号Td； 第一个子系统为重置子系统，其内部封装着图5 所示的递归神经网络，该子系统每5 s 对递归神经网络重置一次；第二个子系统为使能子系统，每5 s 取一个神经网络计算的结果作为推力输出；3 个示波器分别显示推进器推力T，推进器的六自由度合力Ta和推进器推力变化率ΔT。

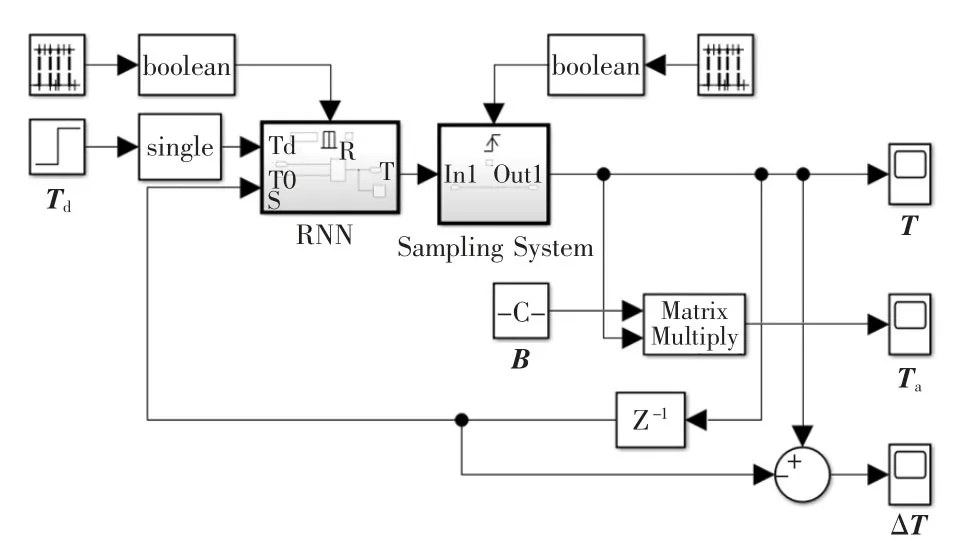
图7 仿真模型Fig.7 Simulation model

仿真时长设为120 s，0～60 s 的Td定义为Td1，值为［2，0，0，0，0，0］；60 s～120 s 的Td定义为Td2，值为［5，0，0，0，0，0］。 仿真结束后，3 个示波器输出如图8～图10 所示。

根据图8 可以发现，在60 s 内，当期望推力在饱和约束范围内时，控制分配下的六自由度合力可以很好地吻合期望推力；60 s 后，当纵向期望推力超出约束范围时，实际推力要小于期望推力，且在约束范围内最大限度的接近期望推力。 如图9 所示，负责提供进退推力的4 个艉推进器在约束下，可以有效地将推力限制在±1 kN 内。 根据图10 可以发现，该方法同样可以将推力变化率约束在±0.1 kN内。

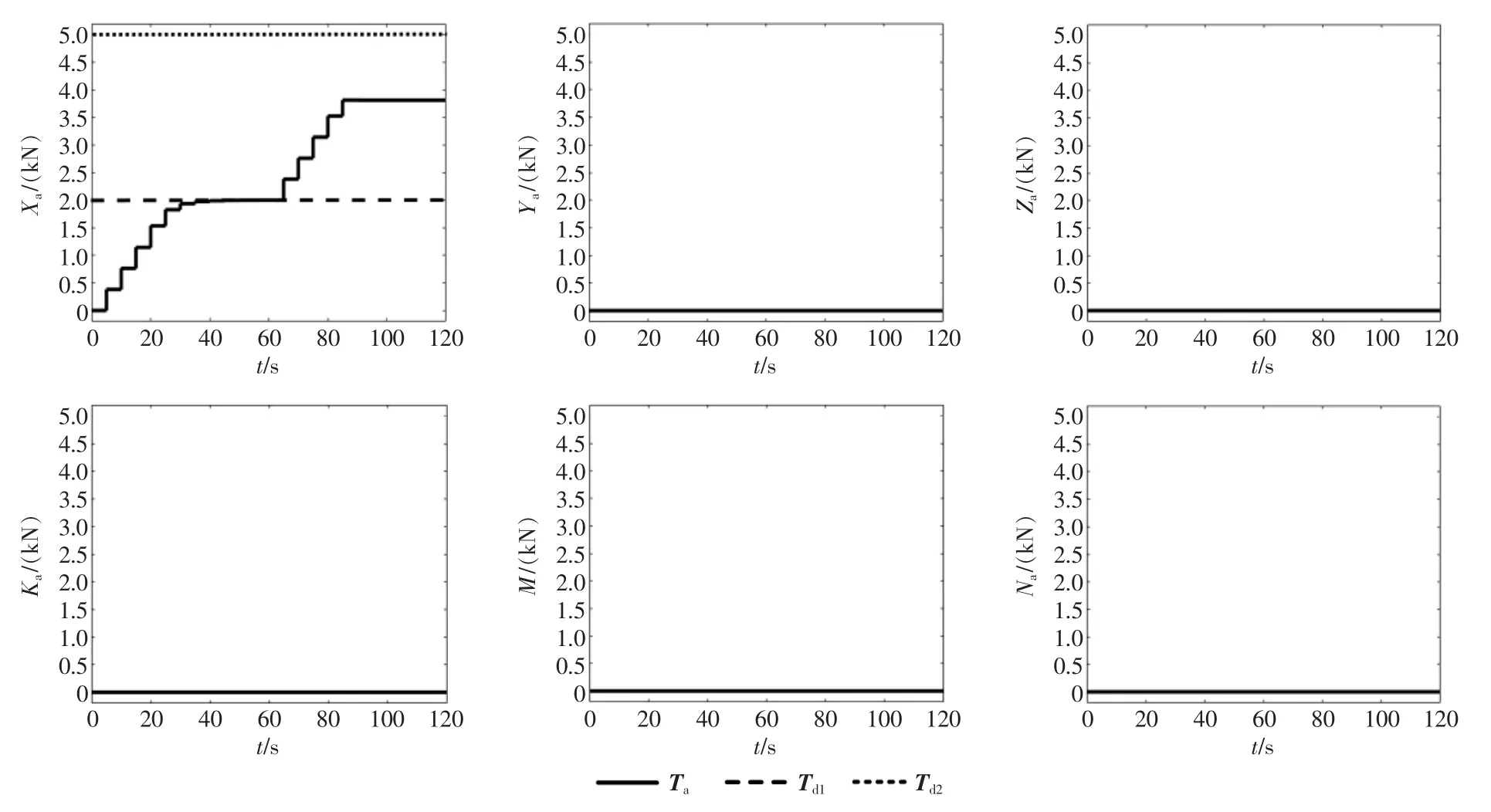
图8 六自由度合力曲线Fig.8 Six degrees of freedom net force curve

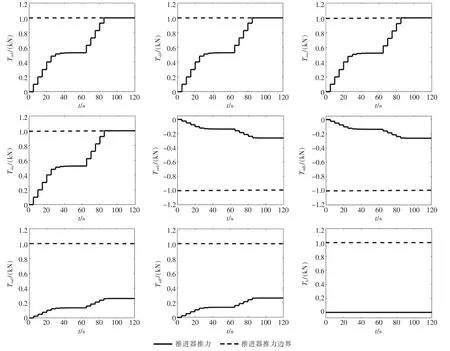
图9 推力曲线Fig.9 Thrust curve

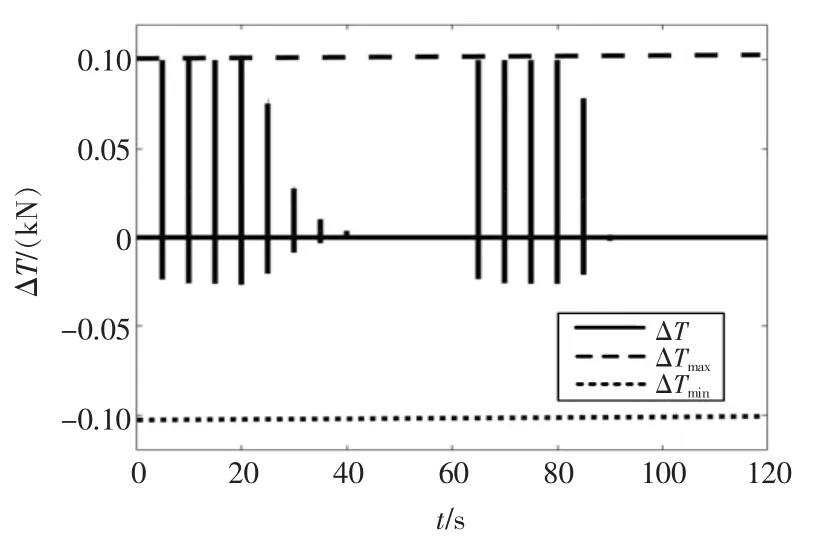
图10 推力变化率曲线Fig.10 Thrust rate curve

为了将递归神经网络配置在FPGA 上， 利用Simulink HDL Code 将仿真模型生成HDL 代码和测试文件，最后实现Simulink 与Modelsim 的联合仿真。 测试文件的仿真结果与Simulink 的运算结果之差如图11 所示。 从图11 可以看出Simulink 生成的测试文件准确，误差始终为零。

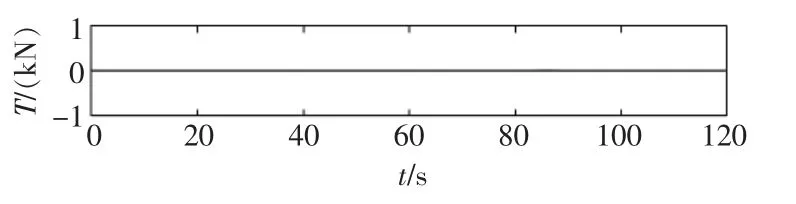
图11 联合仿真误差曲线Fig.11 Co-simulation error curve

需要注意的是，Simulink 的仿真时间与真实递归神经网络的运行时间不同。 对于式（11）这样只含不等式约束的凸二次优化问题，通常用有效集法求解。 本文用Matlab 编写有效集法的m 文件来求解，其求解时间与递归神经网络求解凸优化问题的时间如表1 所示。 通过对比可以发现递归神经网络的实时性更好。

表1 递归神经网络与有效集法求解问题时间Tab.1 Solving time of recurrent neural network and active set method

4 结语

本文对全海深载人潜水器“奋斗者”号的控制分配进行研究。 提出一种基于递归神经网络解决控制分配的方法，该方法可以有效地处理推进器饱和约束和推进器变化率约束。 通过“奋斗者”号载人潜水器半物理仿真平台试验验证，本算法稳定、可靠，计算时间明显优于传统求解优化方法，具有实时性好的突出优点。