纳米孔缺陷导致单层黑磷电荷局域极大抑制非辐射电子-空穴复合的时域模拟

卢浩然，魏雅清,2，龙闰,2,＊

1北京师范大学化学学院，北京 100875

2北京师范大学教育部理论与计算光化学重点实验室，北京 100875

1 引言

近年来，石墨烯和过渡金属硫化物等二维光电材料受到广泛关注。然而石墨烯的零带隙特性使其无法实现逻辑开关，难以在逻辑电路上应用1；而过渡金属硫化物载流子迁移率较低，使其在光电领域的应用受到限制2。与之相比，黑磷具有直接带隙，且载流子迁移率高，引起了人们的极大关注。黑磷是通过层内强sp3杂化共价键和层间弱范德华力构成有序排列的二维层状材料，其具依层数可调节的直接带隙3-7，高度的各向异性3,4和极高的电荷迁移率5,8。黑磷带隙大小随层数减小而增加，层数大于5及块体黑磷的带隙为0.3-0.35 eV，层数小于5时带隙在0.9-1.3 eV6之间，两层时带隙增约为1.36 eV，单层黑磷(monolayer black phosphorus，MBP)也称为磷烯，其带隙可达2.0 eV7。黑磷具有高度各向异性，能够产生晶向依赖的电光导效应，是制造中红外偏振器和偏振传感器的天然材料3。黑磷在室温下的理论电荷迁移率高达10000 cm2·V-1·s-15，实验值也达到了1000 cm2·V-1·s-18，远高于其他二维半导体材料(如二硫化钼，200 cm2·V-1·s-19)。特别地，由于二维黑磷具有良好的电流饱和效应和量子霍尔效应10，具有丰富的电子能带结构11，对紫外光、可见光和近红外光都有着极高的响应度，使得磷烯在光学12、电荷运输13和热电14等领域有着广阔的应用前景。

尽管黑磷具有以上优点，但黑磷的实际应用仍受到一些因素的影响。根据Shockley-Queisser极限效率15可知，单节p-n结太阳能电池光-电转换过程中，未被吸收或者以热量形式散失的能量约占66.3%，其中非辐射电子-空穴复合导致的电荷和能量损失的主要途径。近期实验报道了一系列二维黑磷载流子动力学性质16-18。He等人报道了二维黑磷载流子寿命长达100 ps16。Suess等人报道了少层黑磷的瞬态透射光谱上表现出180 ps和1.3 ns两个尺度的弛豫时间17。Peymon等人利用超快泵浦光谱研究了二维黑磷的光载流子动力学，结果表明相较于多层黑磷，单层黑磷具有更长的载流子寿命(约730 ps)，但该数值明显长于之前的报道，Peymon等将其归因于测试样品中缺陷的影响18。尽管这些实验提供了黑磷载流子寿命相关的重要信息，但并未对不同激发态寿命的物理过程给出令人信服的解释。因此，Long等人采用非绝热分子动力学结合时域密度泛函，研究了双空位缺陷对单层黑磷激发态动力学的影响，发现双空位可以将激发态载流子寿命延长至1.57 ns，而其在完美单层黑磷中为108 ps。该结果解释了Suess报道的两种弛豫时间尺度的起源19。随后，Zhang等人系统地研究了单个磷原子缺陷如何影响单层黑磷的电子-空穴复合动力学，包括磷空位、磷间隙和磷吸附原子。研究发现，只有磷间隙导致复合速率稍微加快，而磷空位和磷吸附缺陷不同程度地延缓了电子-空穴复合20。最近，Guo等人系统地研究了磷的同主族元素掺杂黑磷的非辐射电子-空穴复合动力学，发现复合时间随掺杂元素质量数增加而延长21。

然而这些实验和理论工作仅局限于微小的点缺陷和掺杂对黑磷电子结构和动力学的影响，为了进一步显著的调控黑磷的光电性质，构造大面积的缺陷是一种可能的途径，如纳米孔。由于纳米孔缺陷面积较大，更容易在黑磷中构建出具有特定形状或排列的缺陷体系。而且，尺寸较大的纳米孔比点缺陷对黑磷几何结构的影响要显著。根据构效关系，纳米孔缺陷应该对黑磷的电子结构和激发动力学有更为显著的影响。Cupo等人利用电子束光刻技术制备了具有不同半径的周期性纳米孔缺陷的单层黑磷，并研究了纳米孔尺寸大小和形貌对单层黑磷电子性质的影响，发现缺陷沿之字形方向边缘的自愈作用可以实现材料的半导体性质到金属性质的转变22。但是，他们没有研究纳米孔缺陷对激发态性质的影响，而载流子寿命又是影响黑磷光电器件性能的关键因素。因此，为了厘清载流子寿命和纳米孔缺陷之间的依赖关系，亟待原子尺度的从头算方法系统地模拟纳米孔缺陷如何调控单层黑磷的非辐射电子-空穴动力学。

根据Cupo的实验工作22，本文在单层黑磷中构造了半径为0.43 nm的周期性纳米孔缺陷体系(MBP containing nanopore defects，MBP-ND)。我们采用含时密度泛函理论结合非绝热分子动力学研究了室温下MBP和MBP-ND体系中声子诱导的导带底(conduction band minimum，CBM)和价带顶(valence band maximum，VBM)间的非辐射电子-空穴复合动力学。结果表明，纳米孔缺陷抑制了非辐射电子-空穴复合，使MBP-ND体系激发态寿命延长为完美MBP的约5.5倍，达到2.74 ns，而完美MBP的复合时间约为480 ps，与实验结果吻合较好17,18。研究表明，纳米孔缺陷使体系的带隙增大了0.22 eV，但并未引入隙态。此外，缺陷减小了CBM和VBM的波函数重叠，并抑制了P原子的热运动，使MBP-ND的非绝热耦合强度减小为完美MBP的约1/2。两体系中的电子自由度主要与440 cm-1处的声子振动模耦合，减弱的原子热运动降低了MBP-ND体系的电子-振动相互作用，抑制了P―P键的伸缩运动，导致相干时间延长为完美体系的约1.5倍。三者协同竞争，抑制了MBP-ND体系非辐射电子-空穴复合。该研究结果对指导黑磷光电器件设计，降低非辐射电荷、能量损失和优化器件性能有重要意义。

2 理论基础及计算方法

本文采用含时密度泛函理论结合从头算非绝热分子动力学，研究了MBP和MBP-ND体系的电子结构，明确了面内的P―P伸缩振动贡献了主要的非绝热耦合，诱发了量子退相干，导致了非辐射电子-空穴复合。

2.1 含时密度泛函理论

密度泛函理论使用电子密度替代波函数作为基本变量，采用单电子近似可将有相互作用的多电子问题转化为五相互作用的单电子问题23。基于密度泛函理论的第一性原理计算方法，是根据电子与原子核的相互作用原理及基本运动规律，运用量子力学原理，经过一些近似处理后直接求解薛定谔方程，得到目标体系基本性质的方法。将DFT推广到处理与时间相关的激发态时，就可用其处理多粒子体系的含时问题。实际应用时，体系的电子密度可表示为：

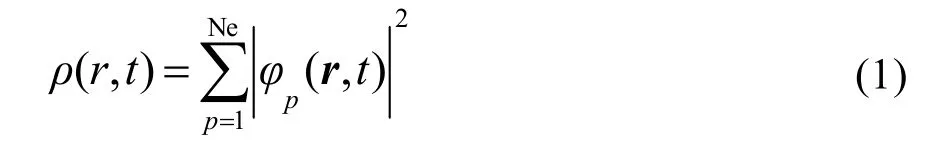
同时波函数φp(r,t)满足时域单粒子 Kohn-Sham(KS)方程24：

满足时域单粒子Kohn-Sham (KS)方程24：

其中Veff代表有效势；

利用变分法可得到时域单电子方程：

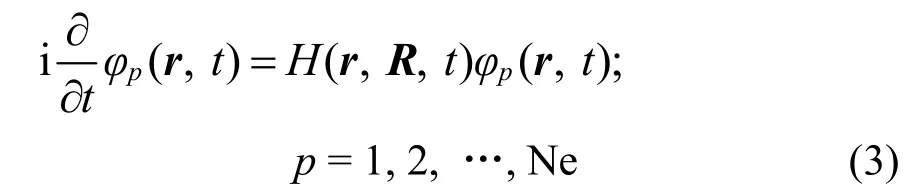
哈密顿量H是由总的电子密度决定的，因此这些方程式互相耦合的。以绝热KS轨道为基础扩展得到时间依赖的KS轨道：

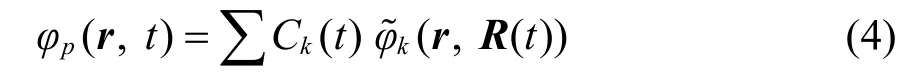
将(4)带回单电子方程(3)得到波函数系数随时间的演化方程：

εk是绝热状态k的能量，djk是状态k和j之间的非绝热(NA)耦合。NA耦合出现是因为电子波函数参数依赖于核坐标，反映了非弹性电子-振动相互作用。NA耦合强度可通过数值方法计算，即相邻时间步间隔的轨道k和j的重叠25

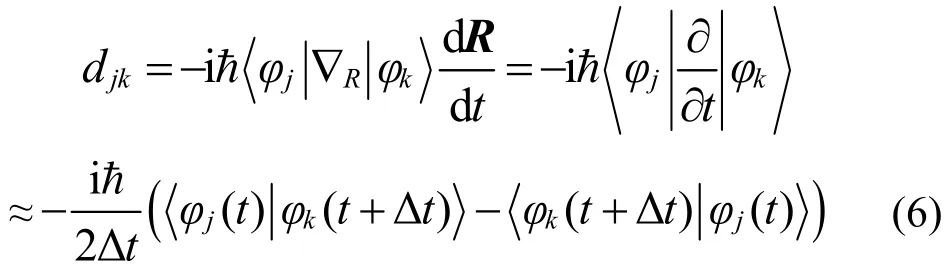
在含时KS理论的基础上，我们采用了退相干诱导的表面跳跃(decoherence-induced surface hopping, DISH)26,27技术。混合量子-经典28的模拟方法将较轻和运动较快的电子被量子力学处理，而较重且运动较慢的核通过经典力学描述。这种方法将电子-核波函数拆解为电子波函数和原子核的经典轨道，将核波包转化为空间中的点。然而在全量子力学的描述中，核波函数以Franck-Condon因子29的形式介入了电子态跃迁速率的表达式。退相干反映了与不同电子态相关的核波包在时间上发散的过程，经过退相干时间后波包重叠减小到零。若退相干过程无限快，可认为动力学是静止的，这种现象可用量子芝诺效应30来描述。退相干与Franck-Condon函数在时间域和能量域之间可以通过傅里叶变换联系起来。由于混合量子-经典方法中不存在核波包，因此退相干必须作为修正引入。DISH将退相干包含到量子-经典非绝热分子动力学中。当退相干发生时，产生随机数ζ，当ζ小于发生跳跃概率时，则轨道跳跃发生；当δ大于发生跳跃的概率时，跳跃禁止。DISH算法在跳跃发生后重新放缩核速度以确保量子-经典总能量守恒。若沿着某方向上核动能分量小于跳跃后电子态跃迁需要吸收的能量，则跳跃被禁止。DISH能够大致维持能量上下跃迁之间的平衡，确保了量子-经典系统在长时间内维持热力学平衡31。此外，经典路径近似的使用极大节约了计算量。这一方法已被证明对大多数纳米材料都是有效的，并得到了良好的结果32。

2.2 谱密度及退相干函数

在光学响应理论中，退相干时间被近似为纯退相时间。原子运动导致电子激发能量波动，波动值δEij是电子态i和j之间能量差，可用自关联函数(ACF)来描述。标准的ACF被定义为

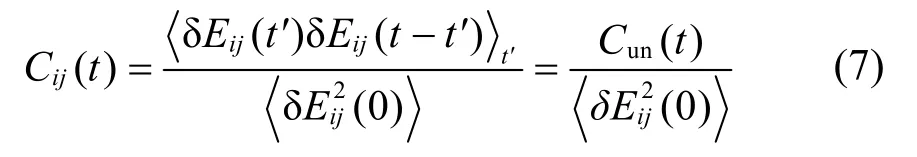
ACF的迅速衰减意味着纯退相过程很快。

经过傅里叶变换得到声子谱密度

它可以识别电子自由度与哪些频率的声子振动耦合，同时声子振动模式的振幅反映了在给定频率下电-声耦合的声子模的强度。

通过对光学响应函数进行二阶积累扩展33，可计算得到纯退相干函数

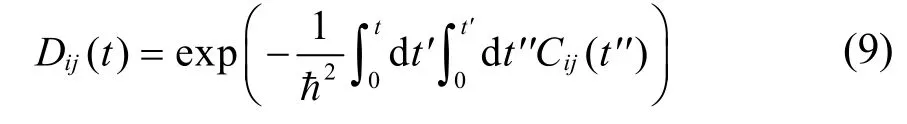
2.3 计算细节

MBP体系由140个磷原子(7 × 5 × 1)超胞代表，其周期性沿XY平面，并在平面法向Z轴方向添加厚度为2.00 nm的真空层以消除周期性层间的相互作用。在MBP体系靠近中心位置选取相邻的8个磷原子去除后形成纳米孔，纳米孔边缘处的悬挂键用氢原子饱和，得到MBP-ND缺陷体系。

利用Vienna从头算模拟软件包(VASP)34来进行几何结构优化、电子结构和绝热分子动力学模拟。利用Perdew-Burke-Ernzerhof (PBE)35来描述非局域电子交换相关的相互作用；利用缀加平面波(PAW)36描述电子和离子实的相互作用。平面波截断能为500 eV，K点网格均采用Monkhorst-Pack方法产生的2 × 2 × 1网格37分别对MBP和MBP-ND进行几何结构优化，随后采用4 × 4 × 1的网格对几何优化后的结构进行态密度(density of state，DOS)计算。将优化后的MBP与MBP-ND使用速率缩放方法升温至300 K；之后以1 fs为步长，在微正则系综下进行6 ps 绝热分子动力学模拟。最后，我们选取了2 ps 的绝热分子运动轨迹，计算了非绝热耦合，并将其平均带隙放缩至0 K下PBE带隙水平后，使用PYXAID程序模拟了两个体系的电子-空穴复合动力学30。

3 结果与讨论分析

3.1 几何与电子结构

黑磷属正交晶系，具有空间反演对称性。图1给出了0 K下MBP和MBP-ND优化后的几何结构。如图1a侧视图所示，MBP由磷原子组成的屈曲六边形构成，包含两个磷原子子层。每个磷原子具有sp3的电子构型并与临近的三个磷原子成键，其中两条P―P键在同一子层，另一条P―P键延伸至另一子层。通过在原始MBP中心处删除8个磷原子，再用H原子饱和缺陷边缘的悬挂键(图中蓝色原子为H原子)构成了MBP-ND(图1b)。优化的黑磷平面均保持平整，说明两个结构比较稳定。0 K时，MBP子层内的P―P键平均键长为0.2220 nm，层间的P―P键平均键长为0.2255 nm。如图1b所示侧视图所示，MBP-PD体系中被氢钝化的磷原子发生了相对明显的位置偏移。特别地，与缺陷中心最接近的四个被氢钝化的磷原子向缺陷中心移动，与之相连的子层内的P―P键平均键长增大至0.2225 nm，而子层间的P―P键平均键长则减小至0.2235 nm。其余四个被氢钝化的磷原子由于位阻较大，主要在子层平面上向缺陷方向偏移。距离缺陷较远的层内P―P键平均键长增长至0.2221 nm，层间P―P键平均键长减短为0.2248 nm。当体系升温至300 K时，两体系的黑磷平面均发生了轻微弯曲，原子核热运动增强，P―P键键长波动大。如表1所示，MBP体系中层内和层间P―P键的键长波动为0.0263和0.0180 nm。而MBP-ND体系中层内和层间P―P键的平均键长波动分别是0.0174和0.0152 nm。表明热运动造成了MBP体系的P―P键长更为显著的变化。就MBP-ND体系而言，纳米孔缺陷附近的P―P键长比其余部分键长波动明显，表明缺陷附近产生了更强的结构变化。

图1 (a) MBP和(b) MBP-ND的俯视图和侧视图Fig. 1 Top (upper panel) and side views (lower panel) of(a) MBP and (b) MBP-ND at 0 K.

表1 300 K下P―P键长波动范围Table 1 Fluctuation range of P―P Bond length at 300 K.

为了进一步表征热运动对几何结构的影响，我们计算了MBP和MBP-ND中的原子涨落的情况。我们使用弛豫过程中原子围绕平衡位置距离变化的标准差来描述原子涨落的大小，。其中σi为标准差，ri为i原子随时间演化位置，＜ri＞为弛豫平均位置。如表2所示，原始MBP中每个磷原子是等价的，MBP-ND中则存在缺陷边缘和杂质原子，分类计算了不同种类原子的涨落情况。MBP中原子振动标准差达0.061 nm，呈现出较大的原子涨落。MBP-ND中，H原子由于自身质量小、体积小振动稍强，缺陷边缘的P原子键长波动大，振动强度稍高于其他位置的P原子，但是总体上缺陷强烈抑制了MBP-ND中的原子涨落，使P原子的平均位置标准差降低至0.051 nm。可见，原子位移标准差的讨论与键长变化分析的结果是一致的。通常，被抑制的原子运动同时降低非绝热耦合强度和延缓量子退相干过程，两者对电子-空穴复合快慢的影响是相反的。

表2 MBP和MBP-ND室温下P和H原子的位置标准差Table 2 Standard deviations of position of P and H atoms of MBP and MBP-ND at room temperature.

图2a，b给出了MBP和MBP-ND体系的态密度图。在PBE水平上计算MBP带隙为0.75 eV，该数值与以前理论计算值19接近，但比实验值38小0.55 eV左右。引入纳米孔缺陷后，MBP-ND带隙增大到0.97 eV。特别地，缺陷并未在带隙中引入缺陷态，这应归因于氢钝化39消除了悬挂键。为了探讨MBP-ND带隙增大的原因，图2c给出了MBP和MBP-ND体系前线分子轨道杂化示意图(仅讨论成键的轨道)。MBP含有不等价的层间P―P键和层内P―P键，导致sp3杂化轨道发生能级分裂，其中层间P―P键较长(平均键长0.2255 nm)，原子轨道重叠较小，能级分裂小；成键时层内P―P键较短(平均键长0.2220 nm)，原子轨道重叠较大，能级分裂大。电子能级由低到高参与形成分子轨道，因此，两个体系的VBM由层间P―Pσ键成键轨道构成，CBM由层内P―Pσ键反键轨道构成。当体系存在纳米孔缺陷时，层间P―P键平均键长缩短至0.2249 nm (MBP: 0.2255 nm)，P原子轨道波函数重叠增大，成键时能级分裂大小由图2c中红色标记扩大至蓝色标记，导致层间P―Pσ键成键轨道VBM下降，从而带隙增加。图3侧视图的VBM电荷密度中，MBP-ND层间P―P键电荷密度分布增大支持了这一观点。由于电子态i和j的非绝热耦合djk可以写成，可见，非绝热耦合与带隙成反比。因此，带隙增加会降低非绝热耦合。CBM和VBM是参与非辐射电子-空穴复合过程的主要的始末电子态，两者的电荷密度分布将对复合过程有重要影响。对于MBP体系，CBM与VBM均匀分布在每个子层P中，这有利于两波函数重叠，增强非绝热耦合强度。在MBP-ND中，纳米孔造成了缺陷附近电子和空穴波函数的消失，显著降低了两波函数的重叠，进一步减小了非绝热耦合强度。如表3所示，MBP体系CBM-VBM间的非绝热耦合强度达0.805 meV，而MBP-ND体系的非绝热耦合强度约为MBP的1/2，数值为0.337 meV。小的非绝热耦合强度会抑制非辐射电子-空穴复合。

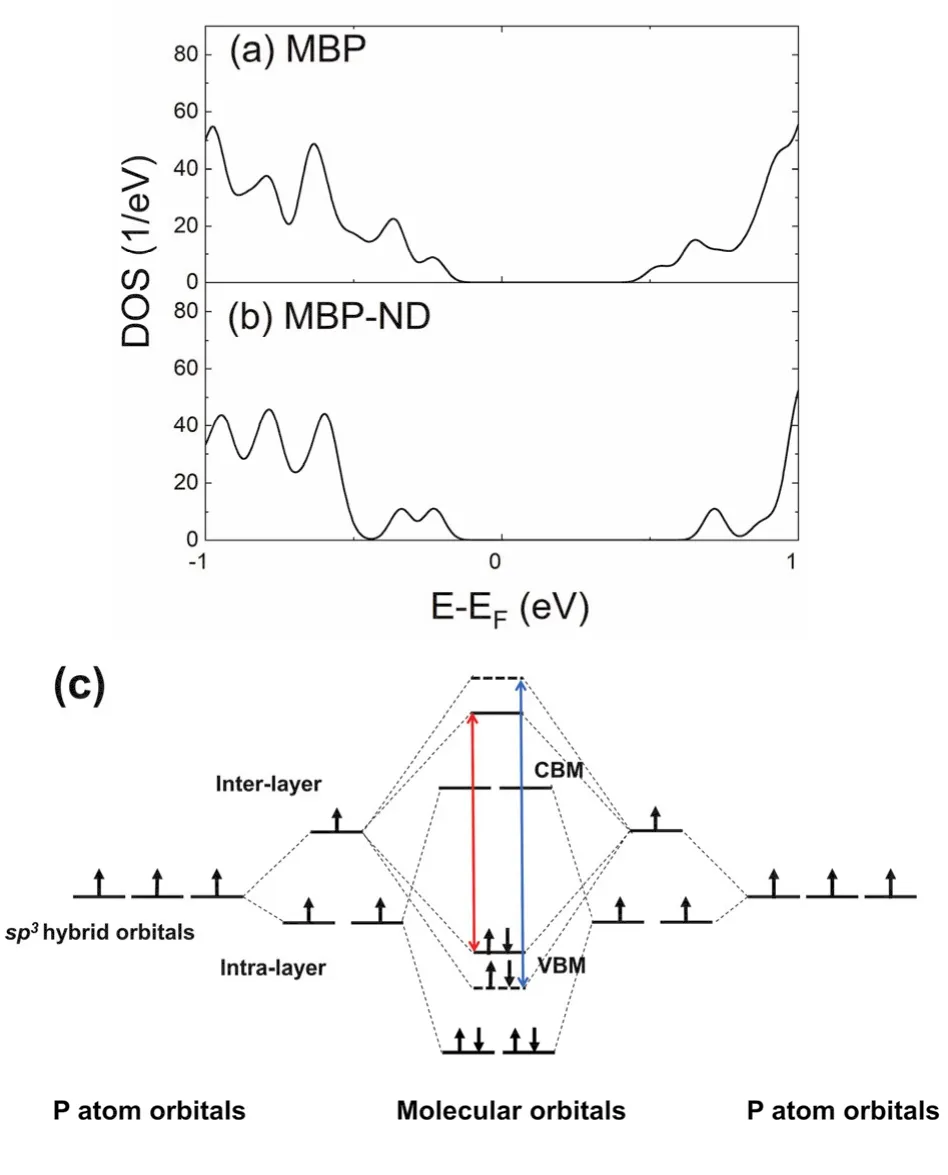
图2 (a) MBP与(b) MBP-ND的DOS图；(c) MBP和MBP-ND前线分子轨道示意图Fig. 2 Density of states (DOS) of (a) MBP and(b) MBP-ND; (c) the hybridization of frontier molecular orbitals in the MBP and MBP-ND systems.

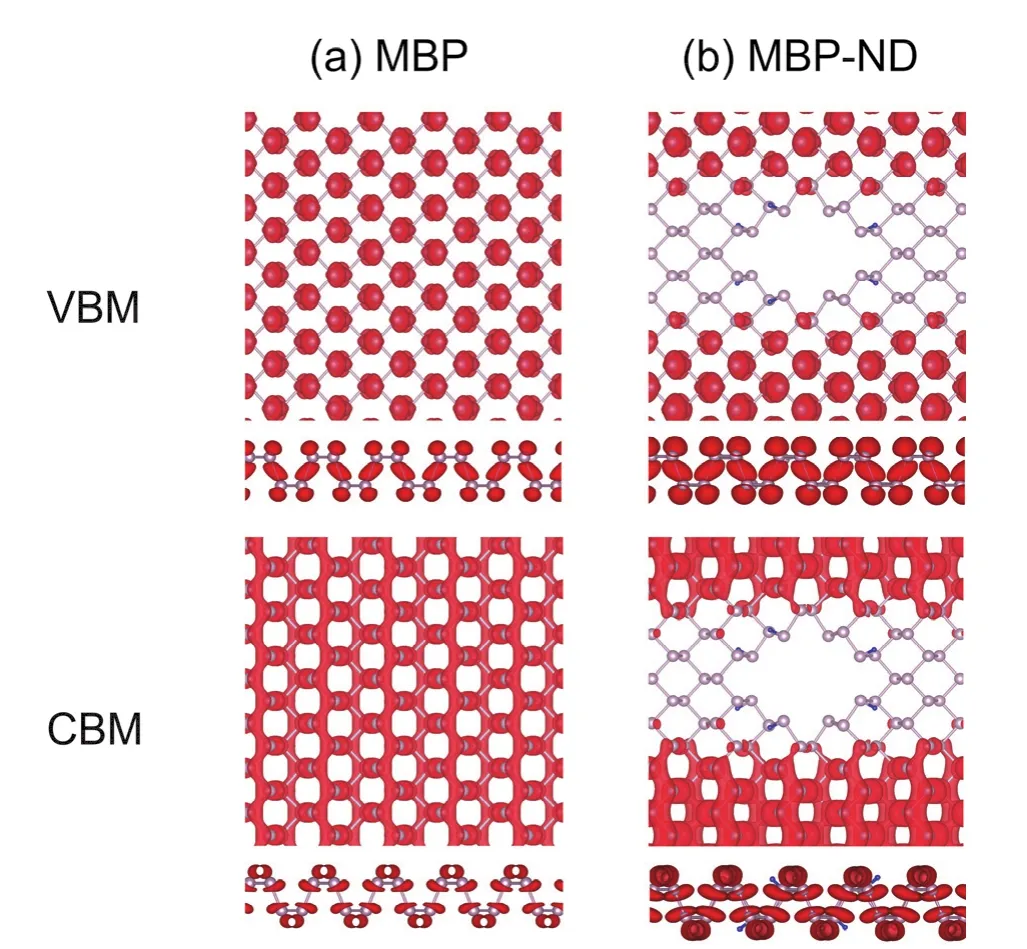
图3 (a) MBP和(b) MBP-ND中CBM/VBM电荷密度图Fig. 3 Charge densities of CBM and VBM in(a) MBP and (b) MBP-ND.

表3 MBP和MBP-ND的带隙、非绝热耦合、退相干时间和非辐射电子-空穴复合时间Table 3 Bandgap, nonadiabatic coupling,pure-dephasing time and nonradiative electron-hole recombination rime of MBP and MBP-ND.

3.2 电子-振动相互作用

电子-振动相互作用可导致弹性电声散射和非弹性电声散射，弹性电声散射可破坏CBM-VBM电子叠加态造成退相干；非弹性散射伴随着电子和能量损失。为了表征MBP和MBP-ND体系中电子-振动相互作用强弱，图4a给出了两者室温时2 ps微正则系综分子动力学轨迹包含的CBM-VBM能隙涨落随时间的变化。有趣地是，MBP比MBP-ND的能量涨落更为显著，表明MBP具有更强的电-声耦合。由表2可知，纳米孔缺陷体系中P原子的热运动受到不同程度的抑制，因而降低了MBP-ND体系能量涨落。为了更好地探究哪些具体的声子振动模式主导非绝热耦合，导致了非辐射电子-空穴复合，我们对VBM-CBM能隙波动的自相关函数做了傅里叶变换，得到声子谱密度图。如图4b所示，MBP和MBP-ND体系中电子自由度主要与440 cm-1处的声子模耦合，440 cm-1的声子模归属于平面内沿之字形方向上P―P键的B2g伸缩振动40，该频率提供了主要的非绝热耦合；此外，电子自由度也与350 cm-1处声子模有较弱耦合，该声子模归属于子层间P―P键指向平面外的Ag1伸缩振动，其对非绝热耦合起次要作用40。但是，由于缺陷降低了MBP-ND中电子-振动相互作用，使得440和350 cm-1的声子模频率的强度均大幅度降低。由于在两个体系中参与耦合的声子模的数目相同，频率的强度反映了量子退相干的快慢。因此，我们推测MBP的退相干时间比MBP-ND的退相干时间短。而退相干过程是影响非辐射电子-空穴复合动力学的又一重要因素。

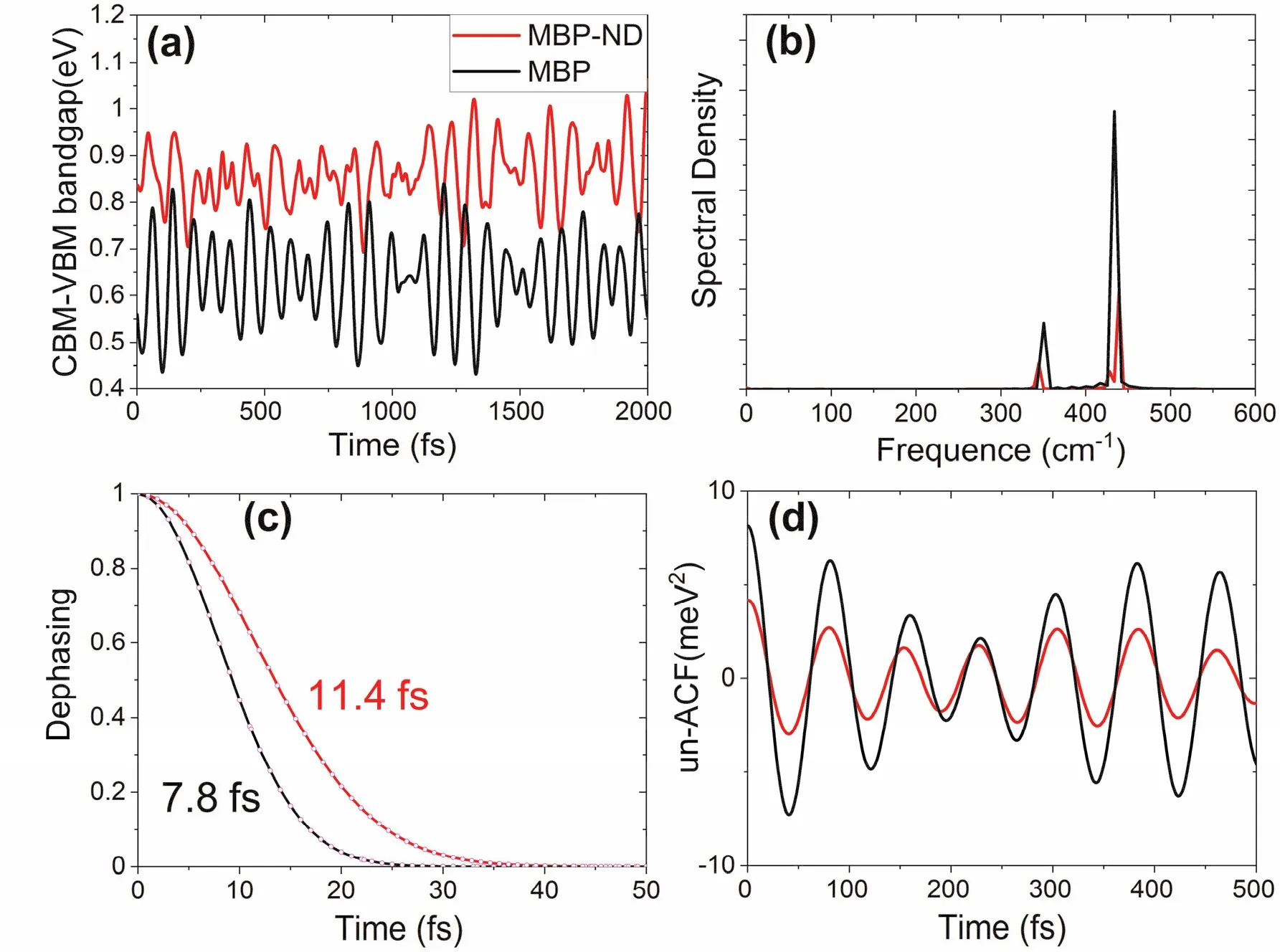
图4 MBP和MBP-ND体系的电子-振动相互作用：(a) CBM-VBM 带隙随时间演化关系，(b) 谱密度，(c) 纯退相位函数。实线为计算的数据，虚线为拟合的数据。(d) 非归一化的自关联函数Fig. 4 (a) The evolution of CBM-VBM bandgap, (b) spectral densities, (c) pure-dephasing function, and(d) unnormalized autocorrelated function (un-ACF) of CBM-VBM transition for the MBP and MBP-ND systems.

为了验证这一猜想，我们计算了两个体系CBM-VBM之间的量子退相干函数，图4c。利用高斯函数:f(t) =Aexp(-0.5(t/τ)2)拟合退相干数据，得到MBP和MBP-ND的退相干时间τ分别为7.8 fs和11.4 fs，MBP-ND的退相干时间约为MBP的1.5倍。根据量子芝诺效应41-43，长寿命的叠加态有利于量子动力学发生，即加快电子-空穴复合过程；反之，当退相干过程变快时，量子叠加态寿命减短，假设退相干过程无限快，则可认为量子叠加态时间足够短，动力学过程不再发生，电子-空穴复合过程被禁止。为了探究MBP-ND退相干减慢的原因，我们计算了VBM-CBM跃迁的非归一化的自相关函数(un-ACF)，如图4d所示。un-ACF是一种可用于分析信号中时域重复模式的便利工具。在累计量近似的条件下，通过积分un-ACF计算出退相干函数。un-ACF的初始值越大，累积积分增长越迅速，则退相干过程越快。两体系的un-ACF函数的振动周期均在76 fs左右，这表明参与退相干过程的主要声子模频率相近，见图4b，因此退相干时间差异源于声子模强度。在振荡周期相近的情况下，MBP的un-ACF函数具有更大的初值，根据方程(9)，MBP体系声子诱导的电子退相干过程更快。

3.3 非辐射电子-空穴复合

图5给出了计算得到的MBP和MBP-ND体最低激发态CBM的布居数随时间的演化图。2.1节“含时密度泛函理论和非绝热动力学”描述了计算方法的理论基础和数值计算细节。通过短时线性近似拟合指数衰减P(t) = exp(-t/τ) ≈ 1 -t/τ得到了表3中的非辐射电子-空穴复合时间τ。图5中的实线是计算的数据，虚线是拟合的数据。如表3所示，MBP体系的电子-空穴复合时间为480 ps与实验数据17,18吻合较好。而MBP-ND体系的非辐射电子-空穴复合发生的时间尺度为2.74 ns，表明缺陷延缓了非辐射电子-空穴复合的发生。非辐射电子-空穴复合受CBM-VBM带隙大小44、非绝热耦合45和退相干时间43三者共同决定。这里，时域的退相干等效于能量域的Franck-Condon因子29,43，而Franck-Condon因子显性地存在于描述量子跃迁速率的费米黄金准则中。短的量子退相干时间对应小的Franck-Condon因子和跃迁速率(长的跃迁时间)。相反，长的退相干时间对应大的Franck-Condon因子和短的跃迁时间。纳米孔缺陷在未引入隙态的情况下，使体系的能隙增大约0.22 eV，降低了非绝热耦合。纳米孔缺陷显著减少了MBP-ND中CBM和VBM的波函数重叠，同时抑制了体系中的原子涨落，进一步使MBP-ND中的非绝热耦合减小约为理想MBP的1/2。同时，被抑制的原子热运动又延长了退相干时间。带隙增加和非绝热耦合强度减小成功战胜了长的退相干时间，抑制了非辐射电子-空穴复合，将载流子寿命延长至2.74 ns。长寿命的激发态有利于降低非辐射电荷和能量损失，提高光电器件的性能。本研究工作表明构建合理数目和形貌的缺陷可以调控黑磷的激发态动力学，该结论可能同样适应于其它二维材料。

图5 非辐射电子-空穴复合过程中第一激发态布居数随时间演化图Fig. 5 The evolution of the first-excited state population characterizing the nonradiative electron-hole recombination.

4 结论

本文采用含时密度泛函理论结合非绝热分子动力学研究了完美单层黑磷和纳米孔修饰的单层黑磷的非辐射电子-空穴复合动力学。研究表明，纳米孔使得缺陷体系带隙增大了0.22 eV 而没有引入隙态，降低了电子和空穴波函数的重叠程度并抑制了原子核热运动，使得非绝热耦合强度较之完美体系减小为约1/2。但是，较慢的原子运动抑制了电子-振动相互作用，降低了P―P伸缩振动的强度，延缓了量子退相干过程，使得退相干时间较之完美体系延长约1.5倍。三者共同作用降低了缺陷体系的非辐射电子-空穴复合速率，将载流子寿命延长至2.74 ns，约为完美体系的5.5倍。完美MBP计算的约480 ps的激发态寿命与实验17,18十分吻合。该研究表明，制造合理数量和形貌的缺陷，如纳米孔，可以降低黑磷的非辐射电子-空穴复合，延长激发态寿命，提高光电器件效率。这一研究对理解和调控黑磷和其它二维材料的激发态性质有重要意义。