对接旧知,循“序”渐进,建模生长
2022-06-20蔡中婷
蔡中婷





摘要:“移多补少”是指研究具有相差关系的两个量,把多的量移给少的一部分,从而使两个量相等的一类问题。文章以“移多补少”拓展性学材开发为例,探究了提升学生思维能力的方法。
关键词:小学数学 促生长 “移多补少” 学材开发
一、对接旧知:唤经验
旧知是新知的基础,会对新知的学习产生影响。因此,在编写拓展性学材时,教师应该对接旧知,激活学生的学习经验。
课本衔接:
①第一行摆:
第二行摆:
第一行比第二行多_____个气球,第二行比第一行少_____个气球。
②明明有5张邮票,东东有12张邮票,东东和明明相差_____张邮票。
解决“移多补少”问题,讨论的是相差数和移动数之间的关系,有时候问题还涉及根据相差数和一个量求另一个量。因此,笔者设计了一组相差数问题,从象形图入手,再到文字表征,契合学生的认知规律,为之后“移多补少”的学习做好基础铺垫。
二、循“序”渐进:建模型
建构主义学习理论强调,教师的讲解并不能直接将知识传递给学生,知识必须通过学生主動建构才能获得。因此,教师必须构建序列型问题组,循“序”渐进,引导学生主动建构模型。
(一)从形入手,建表象
我们从形入手,给学生提供一个认知学习的“脚手架”,帮助学生建立知识表象,再逐渐过渡到抽象表征建模。
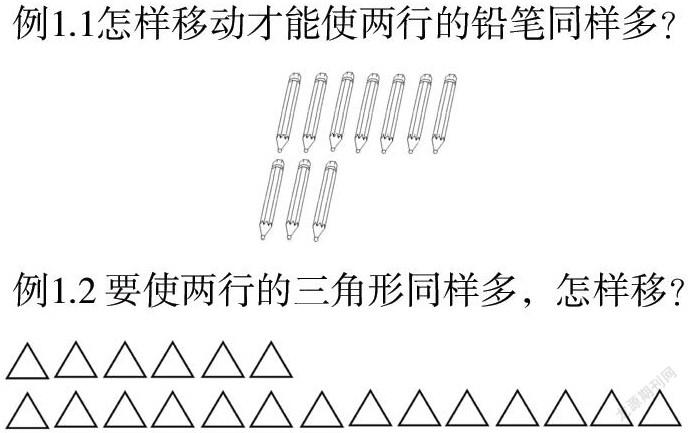
例1.1怎样移动才能使两行的铅笔同样多?
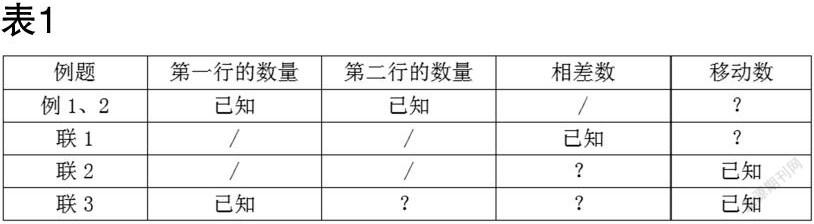
例1.2 要使两行的三角形同样多,怎样移?
上述2个例题构成一组,让学生在纸上“画一画”,如果有困难也可以借助小圆片动手“移一移”,在操作过程中,学生要先找到多出来的部分,然后把多出来的部分其中的一半移给少的。此时,教师的教学重点应落在追问上:“你是怎么移的?”获取学生思维层次。第一层次:移错,把多出来的部分全部移给少的;第二层次:知道不能把多出来的部分全部移给少的,会先一个一个少量移,结果正确但是不知道隐含的相差数和移动数之间的关系;第三层次:先找出相差数,再把多的部分平均分成两份,一份留给自己,一份移给少的,明白其中的隐含关系。通过三个层次的对比,教师分层引导学生对比、讨论,使学生初步建立“移多补少”的认知表象。
(二)动手操作,促认知
例2 动手剪一剪:把两张不一样长的纸条变成一样长,不能丢弃任何一部分纸条。
通过上述在象形图中移一移,学生已初步具备认知表象,但是部分学生对“移动数是相差数的一半”的认识不够立体,所以通过剪纸带的活动,教师将“移多补少”的方法进行半抽象化处理。学生剪出相差部分后,思考移动数时,不像之前的情况可以数出相差部分的数量尝试着移,有“试误”机会,而这里纸带的长度未知,无法“试误”,学生只能动手将多出来的部分对折,沿着折痕剪下后补给少的,两段才会同样长。“对折”这一操作巧妙地让学生感悟到多出来的部分必须平均分成两份,一份留给“自己”,一份移给少的,自然地过渡到“移动数是相差数的一半”的认知。
(三)从数到形,建模型
模型的建构从“形”到“数”,“形”为“数”提供表象支撑,“数”为“形”延伸理解深度。
例3.1 小明有10个苹果,小红有4个苹果,小明要给小红几个,他们才会同样多?
例3.2 小明比小红多6个苹果,小明要给小红几个,他们才会同样多?
之前的例题都给学生提供了辅助的脚手架——象形图,在图的帮助下学生逐渐建立起“移动补少”的认知表象。此时,教师可以适时抽离“脚手架”,以数代形,将信息的表征方式改为文字,将形象认知转化为抽象认知。不同层次的学生可能会有不同水平的解决方式:第一层次的学生可能会自己画出象形图,然后在图上移一移;第二层次的学生可能直接找“相差数和移动数之间的关系”来求“移动数”。
例3.3 小明有10个苹果,比小红多6个苹果,小明要给小红几个,他们才会同样多?
正确的做法有两种:第一种,先求出小红的苹果数量,再求出他们的差,再根据相差数求移动数;第二种,直接根据“小明比小红多6个苹果”得出相差数就是6,再根据相差数求移动数。大多数学生可能会“舍近求远”选择第一种做法。这就是一种思维惯性,即一定先求出另一个未知的量,两个量都已知后,在图上把两个量都画出来,在图上找相差数确定移动数。从内部结构来分析,“移多补少”模型的建立分为两个阶段:第一阶段是在实物图感知经验的基础上建立的,在学生的头脑中有着牢固的表象基础,这种形象支撑让学生更容易理解模型。第二阶段是直接找“相差数和移动数之间的关系”从而确定移动数,是建立在第一阶段基础上的一种理论概括,更具抽象性。它不仅仅是知识层面的拓展,更是一个从形象到抽象的拓展。
所以例3.3存在的目的就是打破思维惯性,让学生理解这个模型的本质是找到相差数从而确定移动数,如果相差数已知就不需要再去求相差数,这个“小插曲”能使学生建立的模型更加完善,对模型的理解也更透彻深入。
(四)逆向而行,固模型
逆向思维也叫“求异思维”,可以想成“反其道而思之”,让思维向对立面发展,从问题的相反面深入探索,进一步完善知识结构。如对例1进行逆向思考,形成可逆关系的一组题。
联1:要使上面一行比下面一行的铅笔多4支,可以怎么移?
联2:上面一行的铅笔移2支到下面一行后,两行的铅笔就同样多,原来上面一行比下面一行多几支?
联3:按要求摆一摆,画一画。要求:从第一行移动2个○到第二行,两行就同样多。
以上题组的内部结构分析如表1所示,联1是将例1、2的条件作等价变换,结构是和例题一致的,联2是例题的逆向结构,即已知移动数反过来求相差数,联3则是在联2的基础上的深化,已知移动数求相差数后,再根据相差数和其中一个量求另一个量。正向和逆向的双向思考,可以使该类型的内部结构清晰明了,更有助于学生建立认知网络结构,巩固模型。
三、多维拓展:促生长
(一)横向而行,拓宽度
1. 拓“对象”,由二元到多元
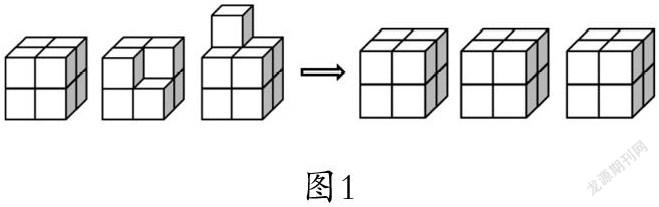
例4.1图1中一共有多少个小正方体?
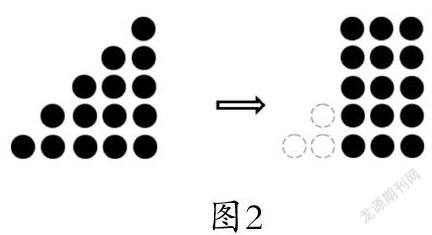
例4.2 图2中一共有多少个棋子?
例4.3 一分钟内,三个学生跳绳分别为80、75、85下,可以把这三个学生的成绩都看成1分钟()下。
例4.4 把下列加法算式改写成加数相同的加法算式。
①4+5+6= ②4+5+6+7+8=
①與原例题相比,对象拓宽,从2个增加到3个,但是解决问题的模型没变,仍然是找相差数后求移动数,但是思维难度加深
2.拓“解法”,由单一到多种
例5 兔哥哥采了6个蘑菇,兔弟弟采了4个蘑菇,兔妈妈把她采的10个蘑菇分给兔哥哥和兔弟弟,怎么分,两人拥有的蘑菇同样多?
这题可以用“移多补少”的方法,先将兔弟弟比兔哥哥少的2个蘑菇补齐,然后将剩下的蘑菇平均分,还可以将三人的蘑菇合起来,再平均分成两份分给兔哥哥和兔弟弟。一题多解能开阔学生视野,丰富学生的解题思路。
(二)纵向而行,拓深度
纵向对问题进行深度上的拓展,即对原问题进行半等价变化,如加强或减弱原问题的条件,可得到原命题的抽象或弱抽象命题,这就是一种半等价变化。
例6.1 哥哥比妹妹多9张邮票,哥哥给妹妹几张后,还比妹妹多3张?
例6.2 哥哥比妹妹多9张邮票,哥哥给妹妹几张后,哥哥反而比妹妹少3张?
例6.3 哥哥给妹妹5张邮票后,哥哥还比妹妹多2张,原来哥哥比妹妹多几张邮票?
例6.4 哥哥给妹妹5张邮票后,哥哥还比妹妹少2张,原来哥哥比妹妹多几张邮票?
这组例题在原例题的基础上,将问题从“同样多”变更为“还比妹妹多3张”,再将“多3张”变更为“少3张”,将问题半等价化拓展深度,通过对比寻“变”,而寻“变”过程中知“不变”,通过多维延伸拓展探寻出“不变”的本质。而例6.3和例6.4则是从逆向角度,同样将问题半等价化拓宽深度,再次在“变”中探寻到“不变”的本质特征,也算从另一个方向验证结果,正向和逆向双向贯通,更能加深学生对知识内部结构的深度理解。
总之,在编写拓展性学材时,教师应注重让学生经历学习序列,感受建模之路,促进学生知识和能力的生长。
参考文献:
[1]喻平.数学教学心理学[M].北京:北京师范大学出版社,2018.
[2]孔凡哲.数学学习心理学[M].北京:北京大学出版社,2012.
(作者单位:浙江省玉环市城北学校)
