爆破振动作用下高层建筑振速变化规律研究

2022-06-17雷兴海

工程爆破 2022年2期

雷振，李卓，雷兴海，游帅，贺路，黄聪

(1.贵州理工学院矿业工程学院，贵阳 550003；2.昆明理工大学公共安全与应急管理学院，昆明 650093；3.贵州大学矿业学院，贵阳 550025；4.贵州大学土木工程学院，贵阳 550025)

随着城市的快速发展，城市交通和住宅拥挤问题成为阻碍城市化进程的一大因素。公路和住宅区的扩(改)建，需要对露天岩土进行爆破开挖，爆破开挖会对周围建筑物产生振动影响，严重时会引起建筑物倾斜、破坏等重大工程问题。由此可知，在爆破施工的过程中，准确地判别和预测爆破振动对高层建筑的破坏影响，对安全施工和经济效益具有重大的实际意义[1-4]。

岩土爆破开挖以其高效、经济的优点被广泛地应用于工程实践中，振动效应作为严重负面效应之一，对工程的施工造成很大的影响[5-7]。目前，露天岩土爆破施工对邻近高层建筑的影响问题日益受到研究者们的关注。建筑物在爆破作用下的破坏机理，为爆破产生的地震波，经过爆源至建筑物之间的地面以及建筑物基底，传递到建筑物的内部，使建筑物结构产生振动[8]。张玉琦等[9]对爆破现场进行振动测试分析，得出地震波在高层建筑中传播，具有明显的高层放大效应，随着楼层的增加，波速先衰减后增大。于蕾[10]通过对低层住宅楼进行爆破振动监测，根据峰值振速的变化规律和爆破振动安全效果，得出爆心距较小时振动主频较高，振动频率大于10 Hz时，随楼层升高无明显的放大效应。王小红等[11]通过对远距离的高层楼房进行了爆破振动监测分析，得出水平方向的峰值振速，中间楼层振速最大，顶部楼层的振速大于低部层楼层，对于垂直方向峰值振速，顶部楼层峰值振速大于底部楼层。高愿[12]通过爆破振动监测数据的分析，总结出混凝土框剪结构高层建筑物随着楼层高度增高，径向振动速度呈减小的趋势；切向、垂向振动速度呈现先减小后增大的趋势。操鹏等[13]监测采石场附近一栋多层建筑物的爆破振动效应得出，爆破作用下，位于爆破远区的高层建筑物，其垂向峰值振速随着楼层的高度增加而增大，水平方向峰值振速随着楼层的高度增加而减小。陈至昊等[14]通过对地铁爆破开挖是对高层建筑的振动危害效应进行监测分析，指出三矢量振速峰值在接近建筑物顶部时出现局部放大效应，位移随楼层的升高逐渐增加。厉建华等[15]针对复杂爆破振动容易引发民事纠纷和造成安全生产事故的问题，通过分析不同振动速度对房屋非结构性损坏的影响规律,确定了振动速度的安全阈值。李顺波等[16]基于几何地震学的基本原理，建立了精确延时逐孔起爆振动峰值预测模型，通过与现场实测进行对比，预测振动峰值与实测振动峰值吻合良好。

综上所述，上述研究方法及研究内容的不同，结果各有自身的特点，对于不同的地质环境和不同结构的建筑物，其研究结果具有一定的局限性。由于爆破振动波的复杂性，不同地质条件下传播特性差别较大，有关露天岩土爆破作用下城市高层建筑的峰值振速变化规律的文献甚少。因此，本文从爆破振动波的传播特性以及建筑物本身的特性出发，研究露天岩土爆破作用下城市高层建筑的峰值振速传播规律，以实现安全、经济、环保的城市绿色爆破。

1 现场测试

1.1 爆破测试场地概况

测试场地位于贵州省贵阳市观山湖区宾阳大道旁山体和小区的高层建筑。高层建筑为框架钢筋混凝土结构，爆破施工时，选用2号岩石乳化炸药，装药结构为耦合连续装药。爆源的对面为城市高层建筑居民区，两者中间为贵阳市外围主干道，日常车流量多。因此，采用了控制爆破减少振动，并对爆破振动进行了实时监控。开挖岩性主要为中硬岩石，单耗为0.32 kg/m3，采用深孔控制爆破和逐孔起爆的方法进行开挖，孔径为0.09 m，孔距为2.5～3.0 m，排距为2.5～3.0 m，孔深为6～7 m。

1.2 测点布置

测试现场布置5个测点，每个测点布置1个传感器，测点布置在距离爆心水平距离为100～150 m的20层建筑内，平均每层高3 m，总高度为60 m。在第1、5、10、15、20层分别布置传感器，对应得测点分别为1#、2#、3#、4#、5#。

爆破振动测试方案：试验方案设计，根据楼房的高度和传感器的数量，每次5个测点布置在建筑物楼梯的转角处，靠近楼房的主立柱，距地面垂直高差分别为0、15、30、45、60 m，5个测点连成的直线与同一排炮孔所在的直线垂直。根据仪器的使用说明，在爆破前用石膏把传感器固定在混凝土地板上，以确保在爆破作用下传感器与建筑物同时振动，准确的测量出振动数据。传感器固定完成后，爆破时提前打开仪器，为了防止仪器的误触发，提前2～3 min开启仪器时间。每次测试严格要求测点的垂直方向保持在一条直线上，因爆破振源位置不同，每次测得振动速度不同。

2 爆破振动速度变化规律分析

2.1 垂向峰值振速

根据实验结果，随机选取4处不同爆源的垂向峰值振速进行研究，垂向峰值振速随楼层高度H变化如图1所示(Q为最大段药量，kg；R为爆心距测点的水平距离，m)。

图1 垂向峰值振速随楼层高度变化

由图1可知，随着楼层高度H的增加，垂向峰值振速v不断增大，在H=0～30 m时，增速较快。H为30～45 m时，增速减小。当H>45 m时，增速与H=30～45 m时相比明显加快。H=60 m处测点的振动峰值速度，约为H=0 m处测点的2.75～3.8倍。垂向峰值振速表现出明显的建筑物高层放大效应。

2.2 切向峰值振速

根据实验结果，随机选取4处不同爆源的切向峰值振速进行研究，切向峰值振速随楼层高度变化如图2所示。

图2 切向峰值振速随楼层高度变化

由图2可知，H=0～15 m时，切向峰值振速快速增加，增速为0.003 6～0.004 9 cm/s，H=15 m处测点的峰值振速，约为H=0 m处测点的1.65～1.84倍。H=15 m为峰值振速增加的拐点，当15 m45 m时，随着H的增加，峰值振动速度也相应增加，增速为0.001 9～0.003 3 cm/s，H=15 m处测点的峰值振速达到最大值。

2.3 径向峰值振速

根据实验结果，随机选取4处不同爆源的径向峰值振速进行研究，径向峰值振速随楼层高度变化如图3所示。

图3 径向峰值振速随楼层高度变化

由图3可知，H=0～15 m时，径向峰值振速随着H的增加而增加，峰值振速初值越大，增速越快。在H=15～30 m时，峰值振速随着H的增加而减小，峰值振速初值越大，减小越快。H=30 m时，峰值振速出现减小拐点，当H=30～45 m时，增速为0.001 5～0.003 4 cm/s。H=45 m时达到径向峰值振速最大值，随后径向峰值振速开始减小。

2.4 三维峰值振速对比分析

选取实验爆源单段炸药量为18 kg，爆心与测点水平距离为100 m的三维峰值振速进行研究，三向振速随楼层高度变化如图4所示。

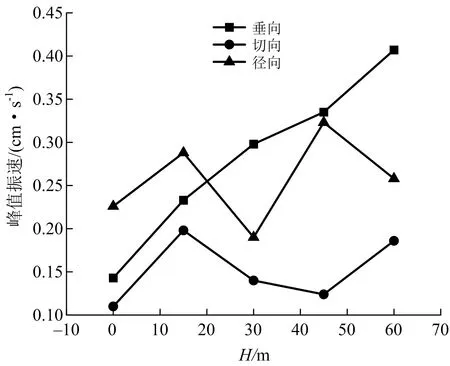
图4 三向峰值振速随楼层高度变化

由图4可知，在H=0 m时，径向峰值振速最大，垂向峰值振速次之，切向峰值振速始终小于垂向峰值振速和径向峰值振速。随着H的增加，垂向峰值振速与径向峰值振速出现交点。随后垂向峰值振速总是大于径向振速。在楼层顶部，垂向峰值振速为径向峰值振速的1.58倍。

根据现场测试结果及上述分析，建筑物顶部的垂向峰值振速远远大于建筑物每个测点的切向和径向峰值振速。

3 城市高层建筑垂向峰值振速计算分析

3.1 高层建筑垂向峰值振速计算公式

城市露天岩土爆破振动符合萨道夫斯基公式：

(1)

式中：v为质点振动速度，cm/s；Q为最大段药量，kg；R为测点距爆心的水平距离，m；k、α为与地质条件有关的参数。

由于建筑物的高度较高，对爆破振动的影响是一个不可忽略的重要影响因素，根据刘美山等[17]的研究和现场实验数据分析，提出基于萨道夫斯基公式的高度修正公式：

(2)

(3)

式中：h为测点距地面的垂直高度；β为与建筑物有关的参数。

3.2 高层建筑物垂向振速计算公式参数分析

通过现场实验数据，对公式(3)中的参数进行分析。对式(3)左右两边取对数，得到公式(4):

(4)

y=A+Bx1+Cx2

(5)

不考虑楼层高度时，利用Origin软件，通过实验数据(见表1)，对A和B进行拟合分析，不考虑楼层高度时1#测点的垂向峰值振速如表1所示。

表1 H=0时测点的垂向峰值振速

自定义拟合函数y=A+Bx1，对表中的数据进行拟合，拟合结果如图5所示。由图5可知，A=5.95，B=2.17，则k=e5.95=383.75。

图5 参数A和B拟合分析

当考虑楼层高度时，利用Origin软件，通过试验数据，对C进行拟合分析，自定义拟合函数y=Cx2-1.973 28，拟合结果如图6所示。由图可知，C=0.02，则β=C=0.02。将参数k=5.95，a=2.17，β=0.02代入式(2)中，可得：

图6 参数C拟合分析

(6)

4 数值模拟验证

4.1 模型建立及参数

以贵阳市观山湖区宾阳大道旁山体和小区的高层建筑受爆破振动影响实际工程为背景，构建与现场实验等比例的三维20层高层建筑模型，建筑层高3 m；x水平向共2跨，每跨5 m；z水平向共3跨，每跨6 m。柱、梁采用ANSYS中BEA M188单元，楼板采用SHELL181单元。经过创建单元，定义材料，定义截面，建立模型，划分网格等操作后，在柱最底面节点施加全约束，建模中单位制采用kg/m/s。

表2 高层建筑参数

图7 不同测点处梁截面等效应力

4.2 数值模拟分析

本次数值模拟采用时程分析法，通过在结构模型的底部输入爆破振动波加速度时程曲线，从结构的初始状态开始，随着爆破振动波载荷的施加，然后逐步进行积分计算，直至爆破振动作用时间结束。即通过积分运算，能够对建筑物的不同楼层速度值变化做定量的研究。通过Origin将实际波形处理为如图8所示的加速度形式，进一步导入模型求解并开展不同楼层速度变化分析。

图8 实测振动波速度、加速度

为验证现场测试结果精准性，对模型进一步开展数值模拟分析，提取不同楼层的速度值，并与现场所测值进行对比与分析(见图9)。

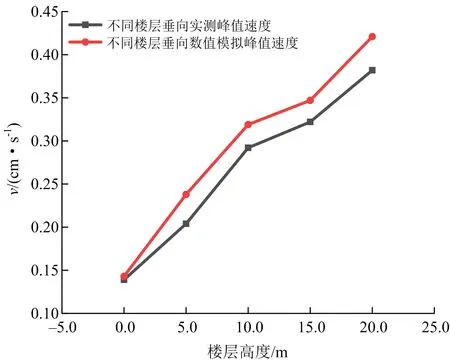
图9 实测、数值模拟峰值振动速度对比分析

对模型第1、5、10、15、20层提取对应节点的速度波形(见图9)，将其与实测的速度进行对比分析，研究结果表明两者误差在20%以内，图中数值模拟结果高于现场所测结果，其原因是建模过程中简化了主、梁等材料，忽略其内部裂隙等造成。

4.3 数值模拟验证

1)加速度验证。为保证本次数值模拟实验精度，在建筑底部通过ANSYS软件自带时间历程后处理提取加速度波形如图10所示，将其与实际导入的加速度波形图对比，发现其振幅变化大致相同，且加速度峰值均在10 m/s2左右波动，可说明本次数值模拟试验具有准确性。

图10 数值模拟节点加速度

2)速度验证。在模型第1、5、10、15、20层提取相对应节点的速度波形，垂向速度从0.142 cm/s增加至0.407 cm/s(见图11)，同理还发现其波形变化趋势基本与实测一致，将本次数值模拟结果与实际所测结果对比，经计算两者误差在20%以内。可较好说明数值模拟与实验结果保持一致。也表明在此类工程案例中，采用数值模拟方法对于高程建筑的速度变化规律研究具有较高的准确性。