μp -bent函数的进一步研究

汪莉婷，姜 妞，卓泽朋，2

（1.淮北师范大学 数学科学学院，安徽 淮北 235000；2.中国科学技术大学 网络空间安全学院，安徽 合肥 230027）

0 引言

布尔函数在编码理论、序列理论和组合设计中具有重要的研究与应用［1］.密码系统中使用的布尔函数要具有良好的密码学性质，如非线性度、代数免疫性［2］、平衡性、弹性［3］等，才能有效抵抗如差分攻击［4］、线性攻击等密码攻击.Rothaus［5］提出非线性度为2n-1-的n元布尔函数是Bent函数（n为偶数）.Bent函数具有最优的非线性度，在所有点处的谱值绝对值都相同，能有效抵抗线性攻击和最佳仿射逼近攻击，在序列、编码等设计中有着诸多应用［6］.关于Bent函数的构造一直是人们研究的重点，除Maiorana-Mcfar⁃land（M-M）构造法［7］和Partial Spread（PS）构造法［8］等直接构造方法外，利用已有的Bent 函数间接构造Bent函数也是常用的构造方法［9］，它可以得到更多具有良好密码学性质的布尔函数，如Carlet［10］提出Bent函数的一种间接构造方法，Zhang等［11］给出一类n+m-2 元Bent函数的二次构造，文献［12］给出n元Bent函数的级联构造.

进行密码分析时，通常假设布尔函数的所有输入向量在进行仿射逼近攻击或快速相关攻击时都是等概率的.如果布尔函数的所有输入的可能性不相等，那么其密码学性质取决于施加在函数域上的概率分布.有偏输入布尔函数与文献［13］提出的随机图理论有着联系，之后，文献［14］也对其理论基础进行讨论.Gangopadhyay 等［15］提出输入向量满足概率测度μp的布尔函数称为μp-布尔函数，并给出一些μp-Walsh-Hadamard 变换的基本性质和μp-bent函数的定义.Mandal等［16］在此基础上间接构造出一些μpbent函数.

本文在Gangopadhyay等人对μp-布尔函数的研究基础上，首先利用二次构造，分析三类不同的μp-布尔函数的μp-Walsh-Hadamard变换的性质，给出其为μp-bent函数的充要条件，并检验n=4 的对称函数的μp-bent函数的性质，之后通过级联方法分别构造1类n+1 元μp-bent函数和2类n+2 元μp-bent函数.

1 预备知识

整数集、实数集和复数集分别用Z、R和C表示，F2为2元有限域，满足1 ≤k≤n的正整数k组成的集合记为[n].当0 ≤p＜1 时，是概率测度为μp(x)的n-维汉明空间，其中概率测度μp(x)=pw(x)(1-p)n-w(x)，x∈Vn(p)，这里w(x)表示x的汉明重量，即令“+”表示Z、R和C上的加法，“⊕”表示F2上的加法.当不需要强调Vn(p)上的概率测度时，用F2n来表示此向量空间.

设a=(a1,a2,…,an)，b=(b1,b2,…,bn)∈F2n，则a·b=a1b1⊕a2b2⊕…⊕anbn，a*b=(a1b1,a2b2,…,anbn).

设复数z=a+ib，则的共轭复数记为，其中a,b∈R，i2=-1.

设函数f(x):Vn(p)→F2，x=(x1,x2,…,xn)，则称f(x)为n元μp-布尔函数，用Bn(p)表示所有n元μp-布尔函数的集合.

设F2n上所有重量为i的向量的集合为En,i={x∈F2n:w(x)=i} ，则En,i的势i∈{0 ,1,…,n} ，且

定 义1［15］设f∈Bn(p) ，则 函 数f(x)在 任 意 点u∈Vn(p) 处 的μp-Walsh-Hadamard 变 换 为

如果对于w(x)=w(y)，有f(x)=f(y)，那么布尔函数f称作是对称的.设对称函数f(x)∈Bn(p)，则函数f(x)在任意点u∈F2n处的μp-Walsh-Hadamard变换可表示为

其中w(x)=i，εi=f(x)，

定义2［15］设1 ≠p∈C，函数f∈Bn(p)，若对任意的u∈F2n，都有|Wf(p)(u)|2=(|ρ|2+1)n，则函数f(x)为μp-bent函数.

定义3设n+1 元布尔函数f(x,xn+1) =f1(x)⊕xn+1(f1(x)⊕f2(x))，其中f1,f2为n元布尔函数，x∈F2n，xn+1∈F2，则称函数f(x)为f1,f2的级联，记作f=f1‖f2.

2 μp-bent函数的构造

二次构造是构造Bent 函数的重要方法，接下来利用二次构造，给出1类r+s个变元的μp-bent 函数的构造，首先给出下面引理.

引理1设函数f1(x)，f2(x)∈Br(p)，g1(y)，g2(y)∈Bs(p).函数G(x,y)=f1(x)⊕g1(y)⊕(f1⊕f2)(x)(g1⊕g2)(y)，则函数G(x,y)在任意点(u,v)∈F2r×F2s处的μp-Walsh-Hadamard变换为

证明由定义1，函数G(x,y)的μp-Walsh-Hadamard变换为

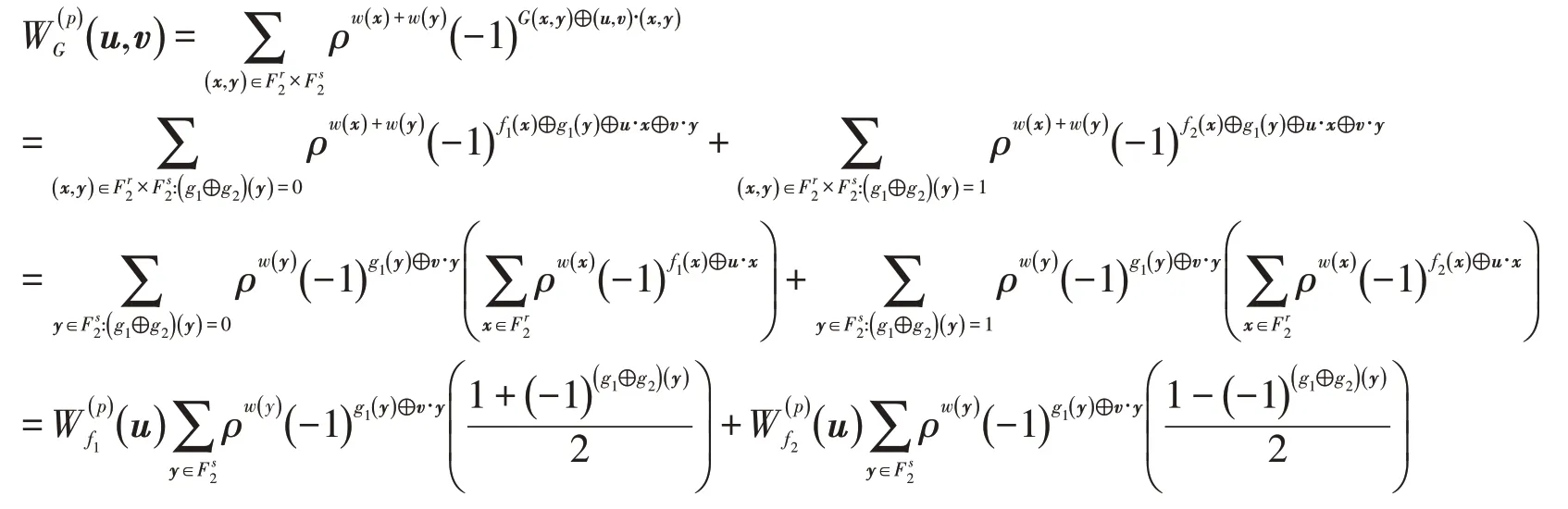
结论得证.

由引理1给出的等式，得到以下结论.

定理1设函数G(x,y)=f1(x)⊕g1(y)⊕(f1⊕f2)(x)(g1⊕g2)(y)，这里f1(x)，f2(x)是r元μp-bent 函数，g1(y)，g2(y)是s元μp-bent 函数，x∈F2r，y∈F2s，则对于任意的(u,v)∈F2r×F2s，函数G(x,y)为μp-bent函数当且仅当

证明令由引理1得

联立式（1）式（2）

当函数G(x,y)为μp-bent函数时，由定义2知，|z|2=( ||ρ2+1)r+s.同理有

根据定理1，下面给出1类r+s+1元μp-布尔函数的μp-Walsh-Hadamard变换.

引理2设函数f(x)，h1(x)∈Br(p) ，g(y)，h2(y)∈Bs(p) ，z∈F2.定义函数G(x,y,z)=f(x)⊕g(y)⊕(h1(x)⊕z)h2(y)，则函数G在任意点(u,v,w)∈F2r×F2s×F2处的μp-Walsh-Hadamard变换为

特别地，当z=0 时，得到如下推论.

推论1设函数f(x)，h1(x)∈Br(p)，g(y)，h2(y)∈Bs(p).定义函数G(x,y)=f(x)⊕g(y)⊕h1(x)h2(y).

（1-1）函数G在任意点(u,v)∈F2r×F2s处的μp-Walsh-Hadamard变换为

（1-2）设f,f⊕h1是r元μp-bent函数，g,g⊕h2是s元μp-bent函数，x∈F2r，y∈F2s，则对于任意的(u,v)∈F2r×F2s，函数G为μp-bent函数当且仅当

证明由引理2，（1-1）得证.根据定理1的证明过程，易证（1-2）.

例1当n=4 时，对于任意的x∈F24，设f(x)=x1⊕x2⊕x3⊕x4，则函数f(x)为μp-bent 函数当且仅当ρ=ib，0 ≠b∈R.

证明由文献［15］中定理9知，如果ρ=ib，那么f是μp-bent函数.因此，只需证明：若函数f(x)为μp-bent函数，则ρ=ib.

令ρ=a+ib，a,b∈R，设w(x)=i，f(x)=εi，0 ≤i≤4，则有

w( )x =i f( )x =εi 0 0 1 1 2 0 3 1 4 0

且f(x)在任意点u∈F24处的μp-Walsh-Hadamard变换为

当u=(0,0,1,1)时，

由μp-bent函数的定义得

故a=0，即ρ=ib.

下面用R(z)和I(z)来表示复数z的实部和虚部.

定理2设函数F∈Bn+1(p),存在函数f(x),g(x),h(x)∈Bn(p),使得F(x,y)=f(x)⊕y(g(x)⊕h(x)),x∈F2n,y∈F2，则

（2-1）函数F(x,y)在任意点(u,v)∈F2n×F2处的μp-Walsh-Hadamard变换为

（2-2）设ρ=ib，0 ≠b∈R，且f(x)，(f⊕g⊕h)(x)是2个n元μp-bent函数，则函数F( )x,y为n+1 元μp-bent函数当且仅当

（2-3） 函数F(x,y)为n+1 元μp-bent 函数当 且 仅 当和

证明由定义1有

故（2-1）得证.

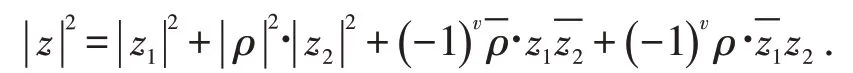
由ρ=ib和f(x)，(f⊕g⊕h)(x)是μp-bent函数可知

当F是μp-bent 函数时， ||z2=( ||ρ2+1)n+1，则，故z1=±z2.反之，当z1=±z2时， ||z2=( ||ρ2+1)n+1，因此（2-2）得证.

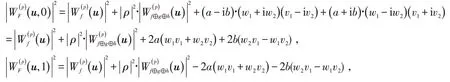
当F是μp-bent函数时，有

则

即

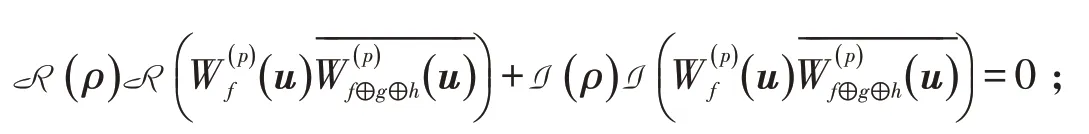
反之，易得F是μp-bent函数，故（2-3）得证.

在构造布尔函数的众多方法中，级联构造也是一种重要的构造方法，利用已有的布尔函数通过级联的方式构造出新的布尔函数，下面利用级联方法构造μp-bent函数.

定理2中，当f1(x)=f(x)=g(x)，f2(x)=h(x)，xn+1=y时，可以得到以下2个推论.

推论2设函数f=f1‖f2∈Bn+1(p)，其中ρ=ib，0 ≠b∈R，f1(x)，f2(x)是2个n元μp-bent函数，则函数f为μp-bent函数当且仅当

推论3设函数f=f1‖f2∈Bn+1(p)，则函数f为μp-bent函数当且仅当

与文献［16］相比，推论2和推论3中级联的函数更具一般性.将函数级联的个数由2个推广到4个，下面给出它们之间的谱值关系.

引理3设函数f=f1‖f2‖f3‖f4∈Bn+2(p)，即函数f(x,xn+1,xn+2)的代数正规型为

其中：f1,f2,f3,f4∈Bn(p) ，x∈F2n，xn+1,xn+2∈F2.则函数f在任意点(u,un+1,un+2)∈F2n×F2×F2处的μp-Walsh-Hadamard变换为

证明由定义1，函数f的μp-Walsh-Hadamard变换为

结论得证.

由上式的谱值关系，给出2类n+2 元μp-布尔函数为μp-bent函数的充要条件.

定理3设函数f=f1‖f2‖f1‖f2∈Bn+2(p)，其中ρ=ib，0 ≠b∈R，f1(x)，f2(x)是2 个n元μp-bent 函数，则函数f为μp-bent函数当且仅当

证明假设对于任意的x∈F2n，有f3(x)=f1(x)，f4(x)=f2(x).由引理3得

则

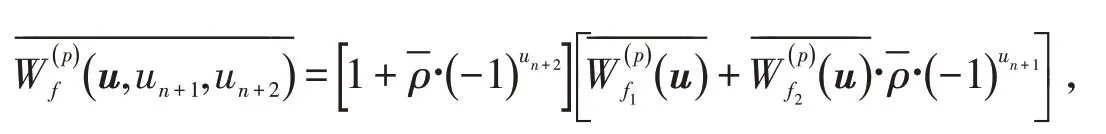
故

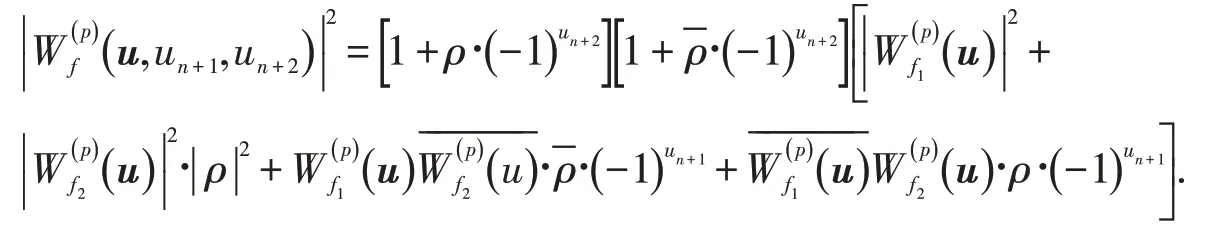
由ρ=ib，0 ≠b∈R 和f1(x)，f2(x)是μp-bent函数，得

当f是μp-bent 函数时，，又

相对于文献［16］，定理3中的函数f2与f1之间没有具体关系，更具有一般性.

定理4设函数f=f1‖f2‖f2‖f1∈Bn+2(p)，un+1,un+2∈F2其中ρ=ib，0 ≠b∈R，f1(x)，f2(x)是2个n元μp-bent函数，则当un+1≠un+2时，函数f为μp-bent函数；当un+1=un+2时，函数f为μp-bent函数当且仅当

证明假设对于任意的x∈F2n，有f3(x)=f2(x)，f4(x)=f1(x).由引理3得

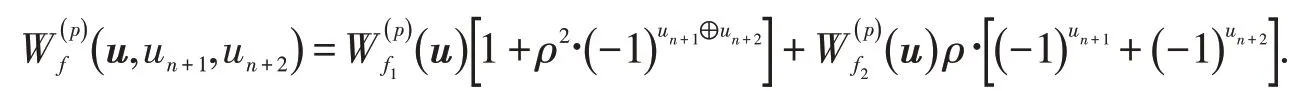
故

由ρ=ib，0 ≠b∈R 和f1(x)，f2(x)是μp-bent函数，得

当un+1≠un+2时, ||z2=(b2+1)n+2，则f是μp-bent 函数.当un+1=un+2时，若f是μp-bent 函数时，或ρ=±i；反之，易得f是μp-bent函数，结论得证.

3 结语

本文在已有的μp-bent函数研究基础上，给出几类间接构造的μp-布尔函数，当选取的初始μp-布尔函数不同时，输出的μp-布尔函数也不同，并通过分析μp-Walsh-Hadamard 变换的性质，得到构造后函数为μp-bent函数时的充分必要条件.在具体应用时，如何根据需要的密码学性质选择合适的构造方法构造出更加合理的Bent类函数是进一步研究的重点.