面板数据均值变点的累积和比值估计

张婷婷，魏岳嵩，董三英

（淮北师范大学 数学科学学院，安徽 淮北 235000）

0 引言

时间序列模型中变点的估计和检验已经得到广泛的研究，随着科技与经济的飞速发展，单个时间序列的分析与研究已经不再满足人们的需求，而面板数据能够提供更多有关模型的信息，从而提高估计的效率.因此将数据集扩展到面板数据上分析是有必要的.

许多专家和学者研究关于面板数据的变点问题，尤其是在经济学、社会科学、质量控制等领域做出诸多贡献.Bai［1］利用最小二乘法和拟极大似然法（QML）分别研究面板数据模型中均值和方差变点问题，证明变点估计量的一致性并给出其极限分布，并表明方差存在变点时，QML比最小二乘法有效.Chen等［2］在Bai的基础上，提出一种累积和法对面板数据模型均值变点进行估计，建立变点估计量的一致性并给出相应的收敛速度，降低文献［1］的计算复杂度.Badi等［3］将Bai的模型推广到非平稳的回归变量和误差项的情况，证明普通最小二乘估计量和第一差分（FD）估计量的相合性并得到其渐近分布.Li等［4］利用累积和（CUSUM）统计量检验面板数据模型中的方差变化.在消除波动性变化的情况下，Shi［5］证明基于平方过程的平方CUSUM 统计量的检验功效优于Li 的检验.Xu 等［6］得到加权平均差统计量的渐近分布.Horváth等［7］利用CUSUM法得到估计量的一阶和二阶渐近性质，并证明变点估计量的极限分布完全由共同因子决定.Chen 等［8］利用非参数局部平滑方法证明平滑变化的参数估计量的一致性.Chan 等［9］得到面板数据变点估计统计量的尾近似值.

本文研究面板数据模型中均值变点估计量的强相合性.文献［10］将一维数据模型推广到面板数据模型，利用累积和比值法来估计均值变点，得到变点的弱相合估计量，但没有给出估计量的收敛速度，本文在文献［10］的基础上，给出变点估计量的强相合性及其强收敛速度.

1 模型及假设

本文考虑的面板数据均值模型为：

其中，{Xij}j=1,2,…,T是独立同分布的平稳随机序列，N为序列的个数，每个序列有T个观测值.k0是所有序列的共同未知变点，且1 ≤k0＜T，当k0=T时，表示该面板数据均值未变化，Zij为面板数据，满足

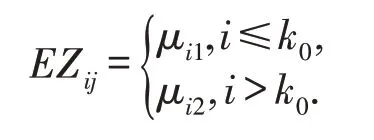
记变化量的跃度δi=μi1-μi2≠0，δi与Xij相互独立.

假设1EXij=EXi=0，，i=1,2,…,N，j=1,2,…,T.

假设2≥k，这里k0是变点的真实位置，k是变点的检测位置.

假设30，0＜α ＜1，即Tα趋向于无穷的速度快于N趋向于无穷的速度.

假设4 对任意的i=1,2,…,N，有Var(Xij)≤C＜∞，其中C为正数.

2 主要结论

对模型（1）的变点k0建立一个累积和比值估计量，即

引理1［11］设Y1,Y2,…,Yn是任意δ阶矩有限的随机变量序列，其中δ≥1，c1,c2,…,cn是任意非负的常数，则有

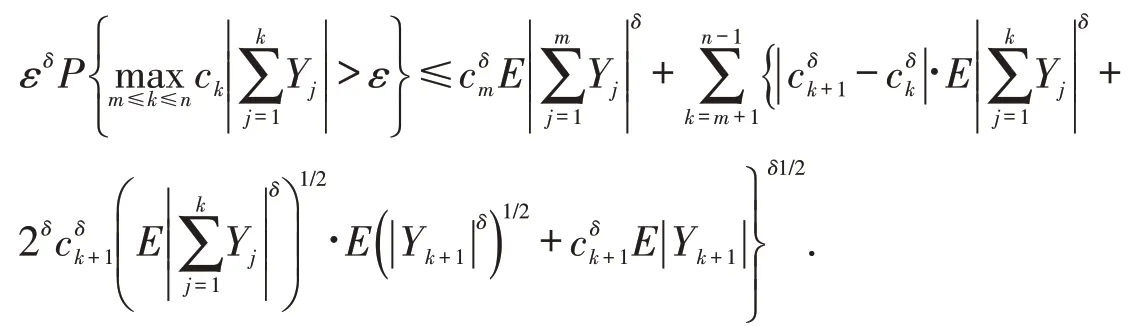
推论1若模型（1）中的假设1~4成立，则T充分大时有

证明先证明式（3）.令Yj=Xij-EXij，m=1，ck=ai1Tγ-1k-γ.

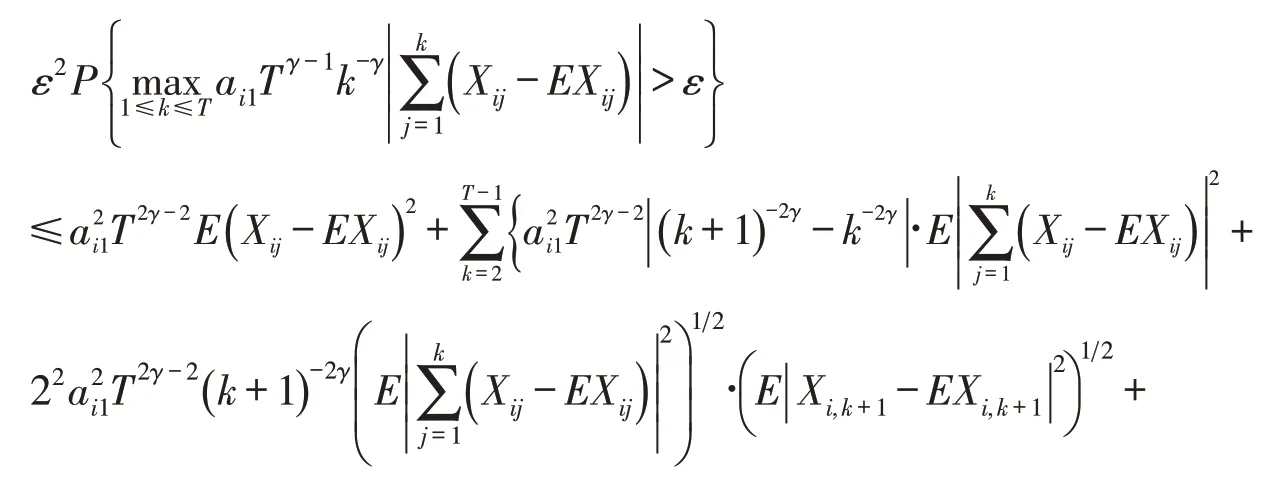
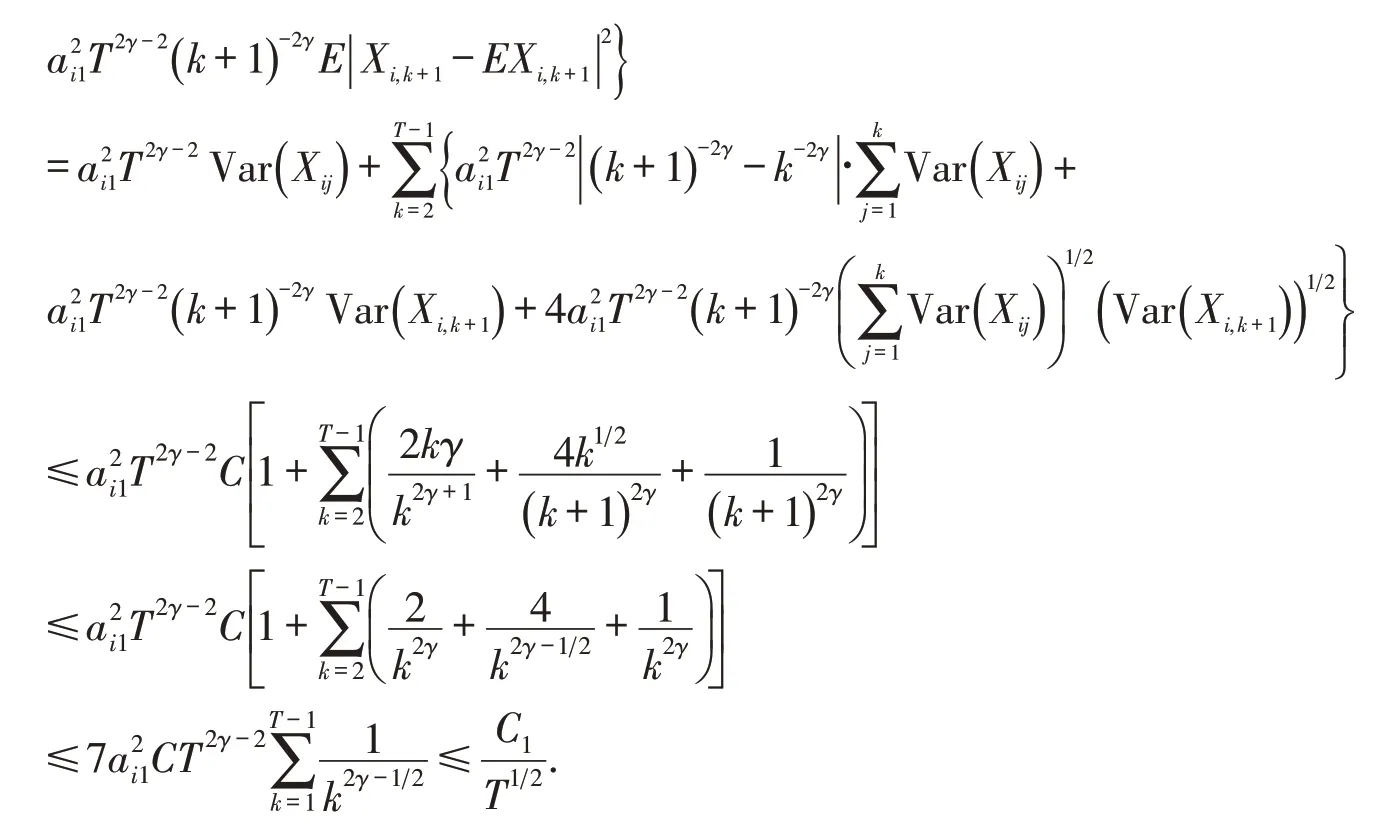
式（3）得证.

式（4）和式（5）同理可证.

定理1若模型（1）的假设1~4成立，则当T→∞,N→∞有θ̂→θ0,a.s.

证明由文献［10］可知，要证明由于

对于I1：记，由推论1，对任意的ε ＞0，T足够大时有

同理可证I2→0,a.s.即对任意的ε ＞0，T足够大时有

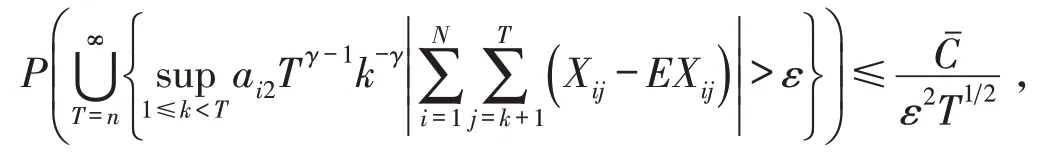
对于I3：对任意的ε ＞0，当T充分大时，有，所以有

即I3→0,a.s.得证.于是

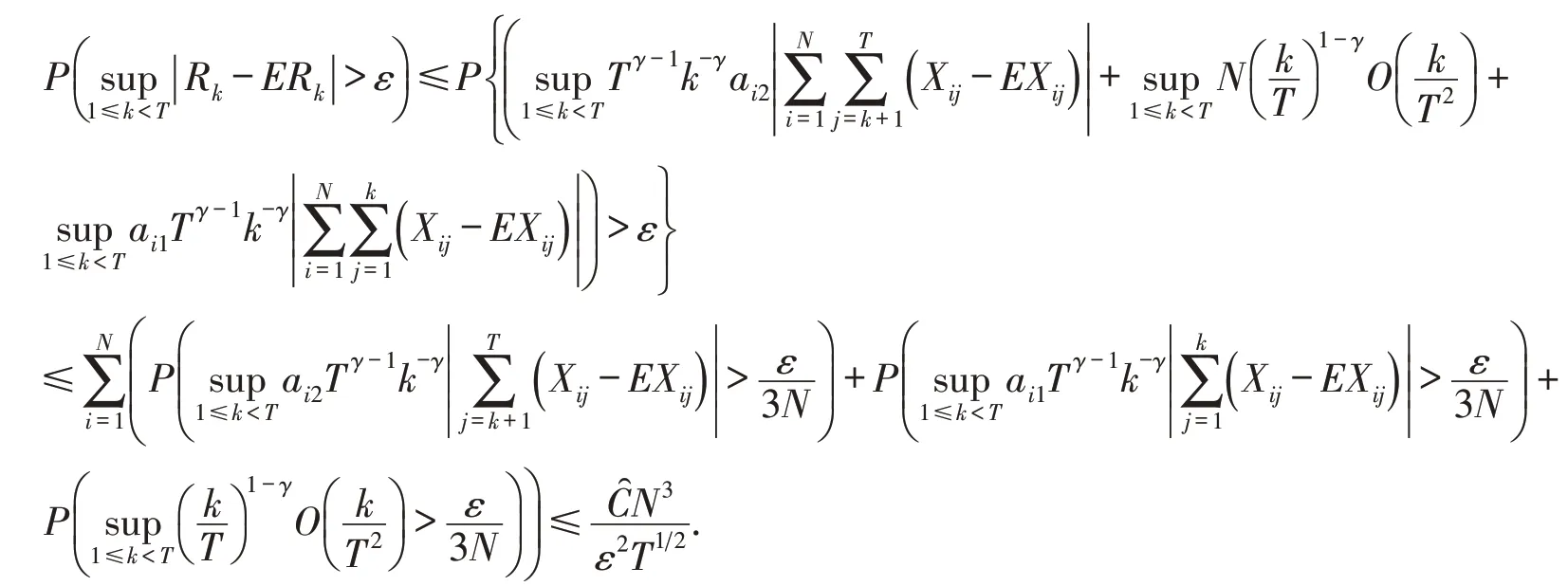
定理2若模型（1）的假设1~4 成立，则有其中T→∞,N→∞时自然数序列M(NT)↑∞.

证明由文献［13］知，要证明定理2，只需证对任意的ε ＞0，有

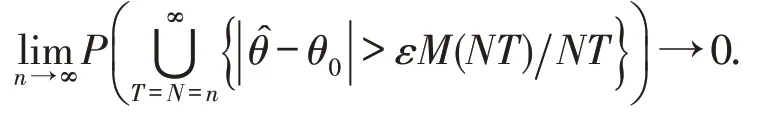
由于θ0∈( )γ1,γ2，其中0＜γ1＜γ2＜1，所以

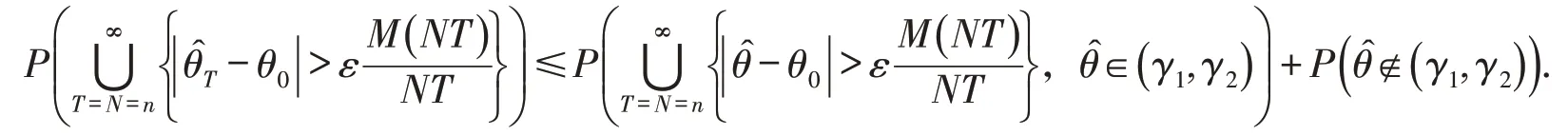
由定理1可知，当T→∞,N→∞时，，不妨设Ai ＞0，由文献［12］知

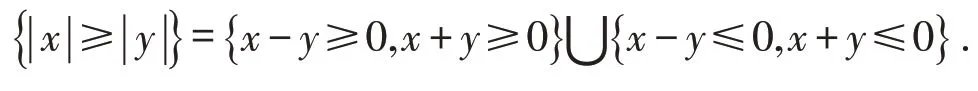
于是有

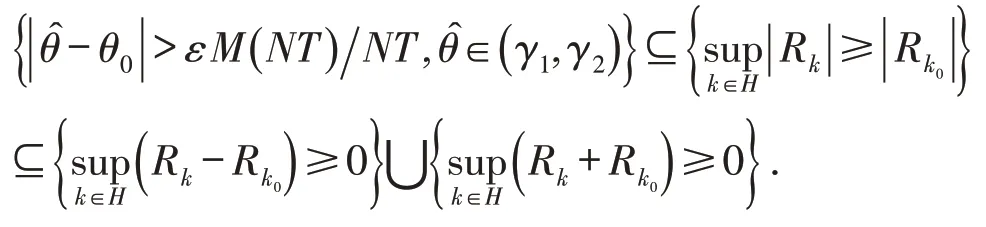
所以只需证明T→∞,N→∞时有

下证式（7），注意到

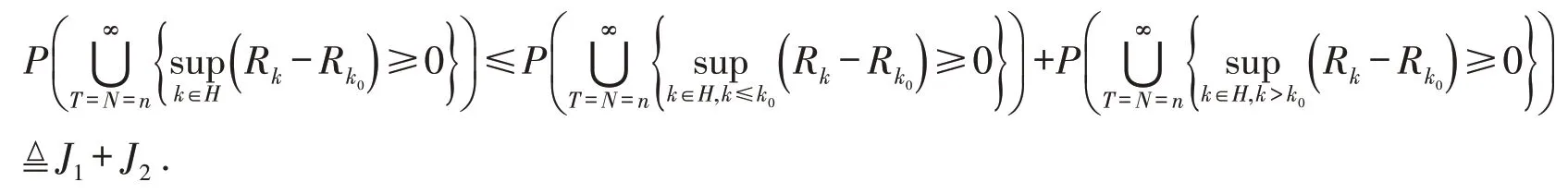
对于J1：

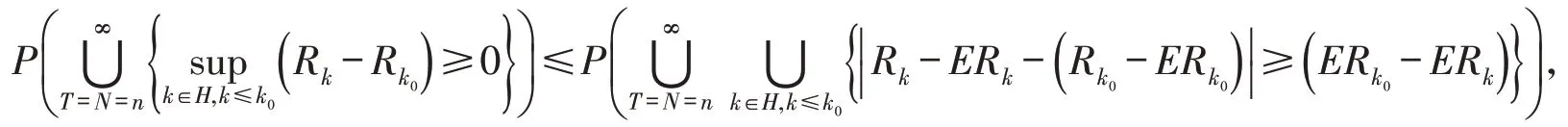
当Ai ＞0，k≤k0,k∈H时有，，又因为

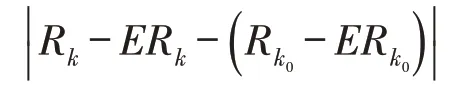
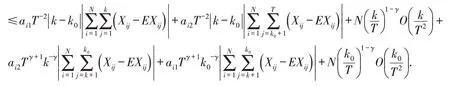
记Vij=Xij-EXij，于是

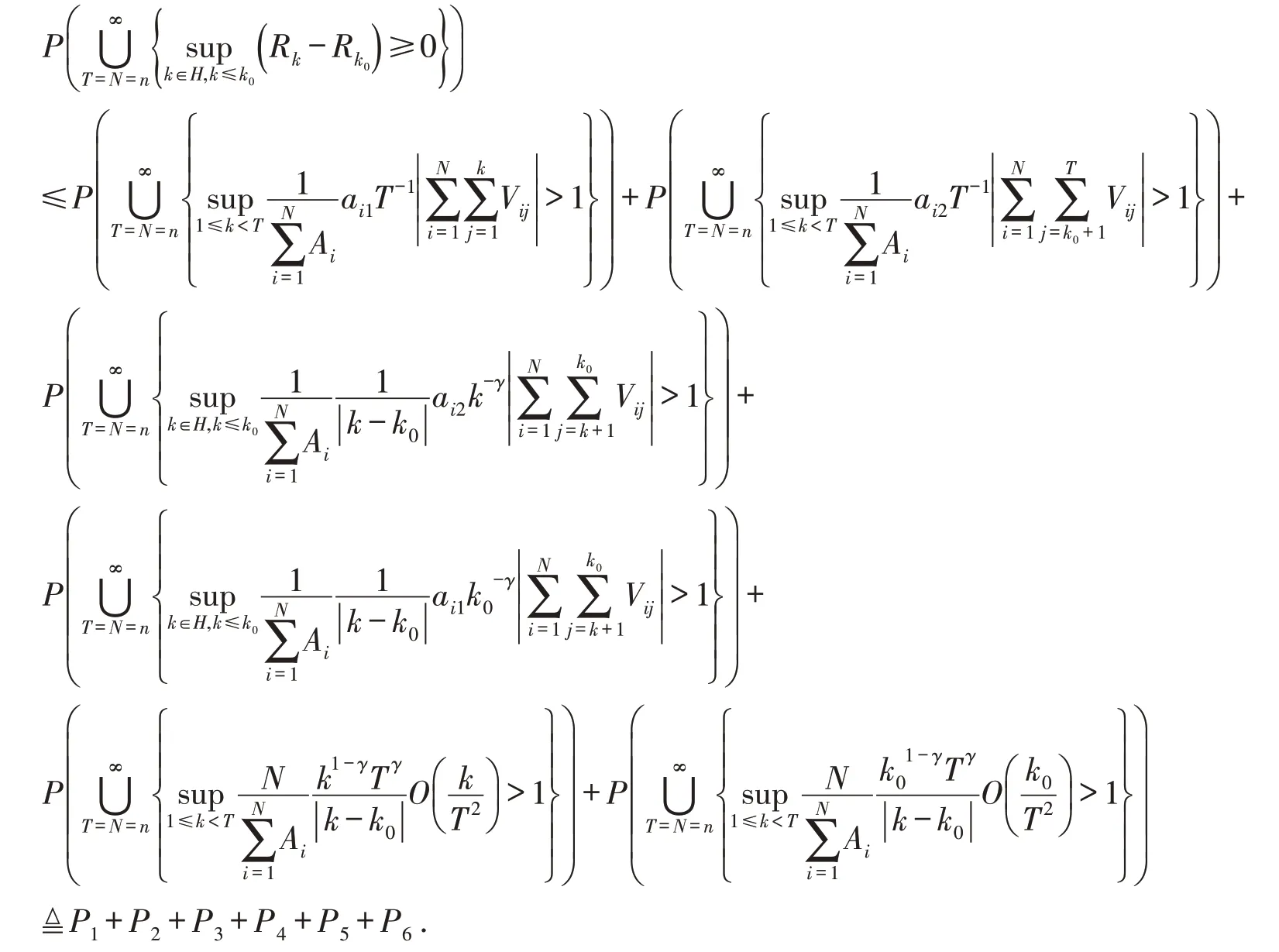
由定理1 可得，当n→∞，γ=0 时，P1→0，P2→0，由推论1 可得，当n→∞时，P3→0，P4→0，由式（6）和假设3可得，当n→∞时，P5→0，P6→0.

故N→∞，T→∞时，有J1→0.同理可得，J2→0.从而式（7）成立.式（8）同理可证.

综上，定理2得证.

3 结论

本文利用累积和比值法研究面板数据模型均值变点估计量的强相合性.当序列数和观测值数都趋向无穷时，定理1和定理2分别给出变点估计量的强相合性和强收敛速度.但这种方法在相依样本序列下并不适用，下一步可以考虑在相依样本序列下面板数据模型均值变点估计量的统计性质.