基于谱配点法的过渡曲面构造

邹 倩

（淮北师范大学 信息学院，安徽 淮北 235000）

0 引言

为探索更有效的曲面造型方法，Bloor 等研究用偏微分方程（Partial Differential Equation.简称PDE）构造曲面的方法，并将其引入CAD/CAM（Computer Aided Design/Computer Aided Manufacturing）领域，曾用PDE方法构造过渡曲面、自由曲面、N边域曲面[1-5].

过渡曲面构造在CAD/CAM中具有重要的地位.其目的是在相关曲面之间生成光滑的过渡曲面.过渡曲面的构造可以看作为如下问题：给定边界为∂Ω的有界区域Ω，求解该区域上满足给定边界条件的曲面X(u,v).典型的边界条件是以X和它的一些导数在∂Ω上的值的形式给出，给定导数的阶数取决于过渡曲面与原曲面的连续阶.

PDE 方法在几何造型中的最初应用就是构造过渡曲面[6-15].过渡曲面可以由椭圆型偏微分方程的边值问题得到，以一阶连续（G1或C1）的过渡曲面为例，只要给定边界曲线和一个跨界导矢，就可以构造出一张光滑的过度面.实际应用中，通常在三维欧氏空间构造一张曲面X=X(x(u,v),y(u,v),z(u,v)) ，x=x(u,v)是参数u,v的函数，参数(u,v)可以视作平面区域Ω中的点.X可以视作由Ω到三维空间R3中的映射X:Ω→R3，当u,v分别为常数时的v线，u线就定义为曲面上的坐标系[9].到目前为止，PDE几何造型方法主要针对调和方程和类双调和方程进行研究.

文献［7］给出四阶椭圆形偏微分方程一类周期问题（对一个自变量是周期函数）的差分解法及在带状过渡曲面、自由曲面设计中的应用，并通过实例讨论通过调整定解问题的参数以修改曲面形状的方法.文献［8］给出Helmholtz 方程的扩展方程：

并将其命名为bi-Helmholtz 方程.受文献［8］启发，由于偏微分方程组中的形状控制参数对PDE曲面的形状影响很大，而现有文献除对边界曲线控制和修改偏微分方程的系数外，对于直接交互式PDE曲面的设计技术较少，且常规的PDE 技术控制整个参数域，局部控制较弱.基于以上几点原因，为进一步提高PDE曲面造型的能力，本文对文献［8］提出的bi-Helmholtz 方程用谱配点法求解其边值问题来构造过渡曲面，并讨论形状控制参数对曲面形状的影响.

二阶bi-Helmholtz 方程：

及周期边界条件

四阶bi-Helmholtz 方程

及周期边界条件

其中X(u,v)=(x(u,v),y(u,v),z(u,v))为三维空间中的PDE曲面，u,v为曲面参数，F(u,v)是力源函数，其中力源函数常取为零，a,b,c为常数[8].

求解区域Ω={0 ≤u≤1,0 ≤v≤2π}，g0(v)和g1(v)为给定的边界曲线，s0(v)和s1(v)为对应边界曲线处的跨界导矢.

1 偏微分方程边值问题的谱配点法

在矩形域Ω=[0,1]×[0,2π]上，考虑如下的二阶bi-Helmholtz 方程.

在x方向上取Chebyshev 点，在y方向上取等距节点为相应节点集上的指数多项式，则插值多项式可写为： 上的Lagrange 多项式，为相应节点集

把式（5）带入式（6）可得

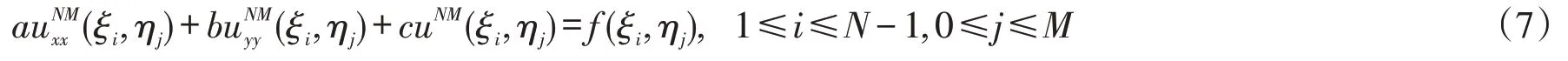
用Dx表示二阶的Chebyshev 微分矩阵，Dy表示二阶的Fourier 微分矩阵，U和F为如下(N-1)×(M+1)阶矩阵：

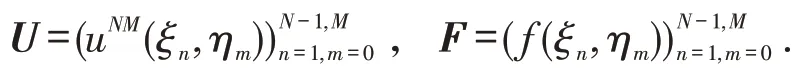
则式（8）可写成矩阵的形式：

标准线性方程组为

其中：I1为M+1 阶单位矩阵，I2为N-1 阶单位矩阵，和ˉ是从F和U的矩阵按列形式展开得到的长度为(N-1)×(M+1)的向量，⊗表示矩阵的张量积.

2 过渡曲面的构造

用偏微分方程边值的方法来构造过渡曲面，其具体步骤如下.

（1）首先根据过渡曲面与原曲面之间的连续阶来确定合适的偏微分方程.例如：若考虑两曲面之间进行GC0拼接，可采用二阶偏微分方程

若两曲面之间进行GC1拼接则需要四阶偏微分方程

（2）确定所需要的过渡曲线，把过渡曲线作为过渡曲面的边界，然后根据偏微分方程的阶数以及原曲面来确定应采用什么样的边界条件以及边界条件值.

（3）通过数值方法求解偏微分方程生成过渡曲面.

下面用实例来说明如何通过谱配点方法来求解bi-Helmholtz 方程构造所需的过渡曲面.

2.1 构造GC0 连续的过渡曲面

考虑(u,v)平面上一个圆与其上方一个球面的零阶过渡，假设(u,v)在区域Ω={0 ≤u≤1,0 ≤v≤2π}内，(x,y)平面上的圆以原点为圆心，半径为R；球的半径为r，球心在(0,0,z0)；取某与平面z=H(0 ≤H≤z0)的交线为过渡线，则其边界条件如下：

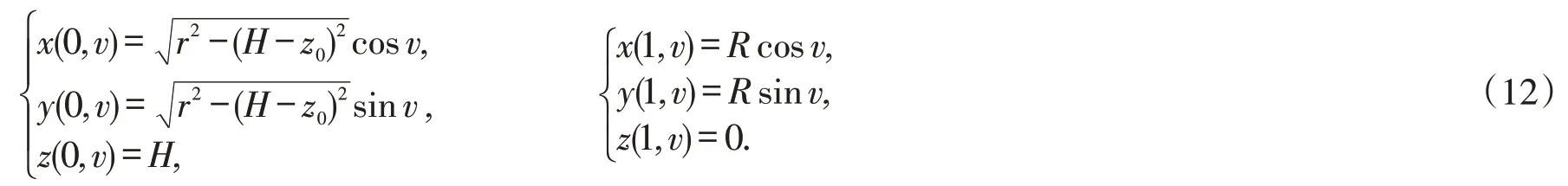
选择二阶bi-Helmholtz 方程式（10），其边界条件由式（12）给出，当r=2，R=3，z0=4 ，H=3，通过谱配点方法式（9）得到上述问题的解.由于Helmholtz 方程具有很好的光滑性，所得过渡曲面也具有很好的光滑性.如图1所示，比较图1（c）和图1（d）可得，当参数a增大时，曲面的形状由上往下向外部膨胀，但整体曲面还是向内凹曲面；比较图1（b）和图1（c）可得，当参数b增大的时候，曲面的形状向内部收缩；比较图1（b）和图1（f）可得，当参数c增大时，曲面的形状向外膨胀，并且曲面由内凹曲面变成外凸曲面.因此可以调节参数a,b,c来控制过渡曲面的形状.

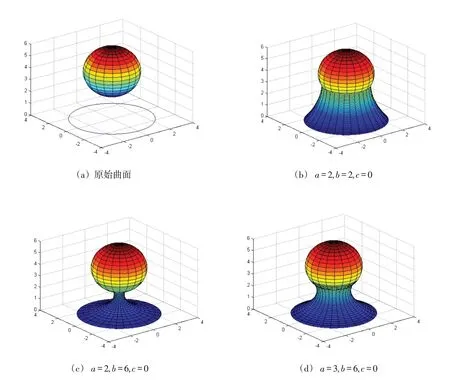
图1 过渡曲面

由上分析可知，不同的参数选取，曲面的形状有着明显的变化.因此可以通过改变形状参数的取值来改变过渡曲面的形状，而且可以通过3个形状参数a,b,c来调控过渡曲面的形状，因而可以更加灵活地调控过渡曲面.

2.2 两圆柱面间过渡面的构造

要求在2 个互相垂直的圆柱面之间构造一阶连续的过渡面，不妨设两圆柱面的表达式分别为x2+y2=r2和y2+z2=R2.

过渡线分别为x2+y2=r2，z=H和y2+z2=R2,x=h.其参数化方程为：

依据一阶连续过渡条件，可得切矢边界条件如下：

式中S1,S2分别为沿边界z(0,v)和z(1,v)的跨界导矢.

使用四阶bi-Helmholtz 方程式（11），通过谱配点法式（9）可以得到问题的解，当r=3，h=5，H=3，R=3，S1=-2，S2=3 时，所得曲面如图2所示.

图2 两圆柱面间的过渡面

3 结论

本文阐述二阶和四阶bi-Helmholtz 方程的一类周期边界问题的谱配点法解法及其在过渡曲面设计中的应用，它不同于传统的PDE方法中的二阶和四阶的偏微分方程，比传统的二阶和四阶偏微分方程有更多的形状参数，有3个形状参数a,b,c来调控过渡曲面的形状.因此在曲面设计时，可以更加灵活控制过渡曲面的形状，这样设计者可以更加方便地设计出想要的过渡曲面，对曲面设计具有重要意义.