随机丢包不确定的网络控制系统H∞滤波
2022-06-17马运强王宗跃
马运强,王宗跃,甘 泉
(1.安徽机电职业技术学院 电气工程学院,安徽 芜湖 241000;2.淮海技师学院 机电工程系,江苏 宿迁 223800)
0 引言
随着我国智能制造加快推进,基于点对点线路连接实现数据信号传输的经典控制系统已经很难满足当前大规模复杂工业控制系统的需求[1-2].运用网络技术将传感器、控制器和执行器等连接,而构建的网络控制系统(Networked Control Systems,NCS)已经成为当前工业领域发展的重点方向[3-4].NCS具有优化线路、易于装调维护、资源共享等优点,但是由于网络技术的介入,对控制系统的分析也带来新的挑战,网络通道资源有限,数据传输中易发生时延或丢包等现象,将造成控制信号丢失及性能指标降低等问题[5-7].针对网络控制系统存在随机丢包和外部信号扰动问题,将设计滤波器滤除干扰,恢复系统信号[8].网络控制系统常采用的滤波器包括H∞滤波器[7-9]、H2滤波器[10]、l2l∞滤波器[11].
近年来,关于网络控制系统的研究得到一定发展.王科举等[12]探究存在随机时延和丢包的网络控制系统控制器设计问题,引入线性变换方法将随机时延过程等效为无时延过程,设计一种新型丢包补偿方法,具有一定的抗干扰能力.Ren等[13]探讨多通道丢包与通信制约的网络化系统,由于网络通信限制采样周期内仅发送单个数据包,运用Markov链刻画网络数据包传输过程,但是结论不适用H∞滤波器.Liu等[14]利用随机伯努利序列建立不确定多数据包丢失的模型,研究一类不确定H∞滤波器设计问题,基于随机理论和线性矩阵不等式方法给出滤波器存在的不等式判据.张端金等[15]考虑双边数据丢失和随机时延的离散Delta控制系统,研究一类H∞滤波器设计方法,运用离散伯努利随机序列描述双边数据丢失现象,给出滤波误差系统H∞性能指标与滤波器增益之间的关系.
本文针对存在随机丢包及参数不确定的网络控制系统问题,提出一类H∞滤波器设计方法,引入随机变量θ(k)刻画网络数据丢包问题,θ(k)满足随机伯努利序列特征,运用矩阵不等式形式给出H∞滤波器存在的充分条件.
1 建立模型
考虑不确定的网络控制系统,其状态表达式:

其中,x(k)∈Rm为系统的状态数据,y(k)∈Rn为系统的测量数据,z(k)∈Rp为系统的估计数据,w(k)∈l2[0,∞)为能量有界的扰动输入信号.和ΔB为具有合适维数的不确定矩阵,和L1为具有合适维数的确定矩阵,不确定参数矩阵[ΔA ΔB]=MF(k)[N1N2],M,N1和N2为具有合适维数的确定矩阵,并满足FT(k)F(k)≤I.
考虑网络信号不稳定及堵塞等问题,传感器测量数据在传输中易出现丢包现象,引入随机变量θ(k)刻画网络数据丢包问题,θ(k)满足随机伯努利序列特征.θ(k)=1,表示控制系统传感器测量数据未发生丢包,滤波器接收数据为当前输入数据,yˉ(k)=y(k);θ(k)=0,表示控制系统传感器测量数据发生丢包,滤波器接收数据为零,0.随机变量θ(k)为0或1,θ(k)概率特性描述为:

综合所述,滤波器的接收数据为:

设计离散滤波器,其状态表达式:

其中,xf(k)∈Rm,yˉ(k)∈Rn,zf(k)∈Rp分别为滤波器的状态数据、接收数据和输出数据,Af,Bf和Cf为具有合适维数待确定的参数矩阵.
结合式(1)、式(3)及式(4),增广滤波误差系统模型,定义增广向量,滤波误差e(k)=z(k)-zf(k),滤波误差系统状态表达式:

考虑网络控制系统,目的是设计如式(4)描述的滤波器并使其满足:
1)当扰动输入信号w(k)=0,滤波误差系统(5)是随机稳定的,即
2)当扰动输入信号w(k)∈l2[0,∞)和零初始状态,对于任意正值γ,滤波误差系统具有H∞性能指标,即,那么,滤波误差系统是随机稳定的,并具有H∞性能指标.
2 滤波性能分析
定理1考虑网络控制系统,对于任意正值γ,若存在正定矩阵P和Q,使得不等式(6)成立:

那么,滤波误差系统是随机稳定的,并具有H∞性能指标.
证明取Lyapunov函数V(k)=xT(k)Px(k)+xfT(k)Qxf(k).函数V(k)的差分方程为:

将θ(k)BfC分块为θBfC+η(k)BfC,θ(k)Bf B2分块为θBf B2+η(k)Bf B2,其中,η(k)=θ(k)-θ.根据式(2)得E[η(k)] =0,E[η(k)2]=ξ,代入式(7),得:
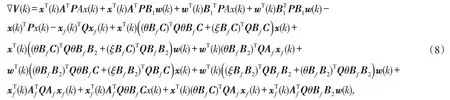
1)当扰动输入信号w(k)=0,证明滤波误差系统具有随机稳定性.式(8)等效为:
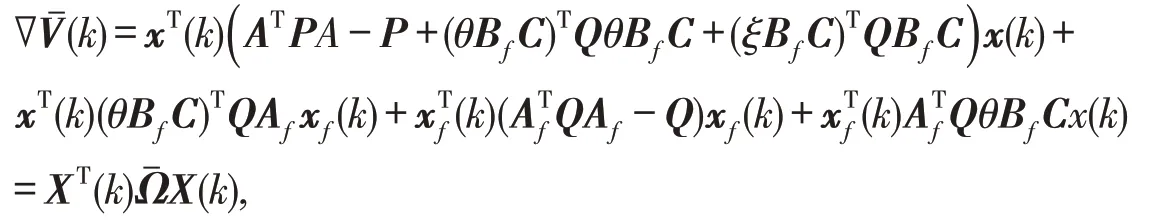
若定理1成立,那么不等式(6)隐含Ωˉ<0,即∇Vˉ(k)<0,得:


则滤波误差系统具有随机稳定性.
2)当扰动输入信号w(k)∈l2[0,∞)和零初始状态,证明滤波误差系统满足H∞性能指标.

其中,

由Schur补定理可知,不等式(6)等效于Ω <0 ,进而J(k)<0,即:

对式(9)累计求和,得:在零初始状态下V(0)=0,V(∞)>0,代入式(10),得那么,滤波误差系统具有H∞性能指标.

3 滤波器设计
定理2考虑网络控制系统,对于任意正值γ,正定矩阵P和Q,矩阵J,U1,U2和U3,滤波器式(4)存在的充分条件需使得不等式(11)成立:

那么,滤波器参数矩阵为:Af =J-TU1,Bf =J-TU2,Cf =U3.
证明式(6)含有不确定项F(k),无法直接求解滤波器相关参数,运用分解法,变形为:

根据文献[14]引理2得式(12)等价为:

根据Schur补定理得式(13)等价为:

由于式(14)含有非线性矩阵-P-1和-Q-1,运用线性矩阵不等式方法计算复杂.引用矩阵J,对式(14)左 乘G=diag[II I I JTJTJTII] ,右 乘GT.由 于P为 正 定 矩 阵,并 满 足(J-P)P-1(J-P)T≥0,展开得-JTP-1J≤P-J-JT,同理得-JTQ-1J≤Q-J-JT,代入式(14),得:
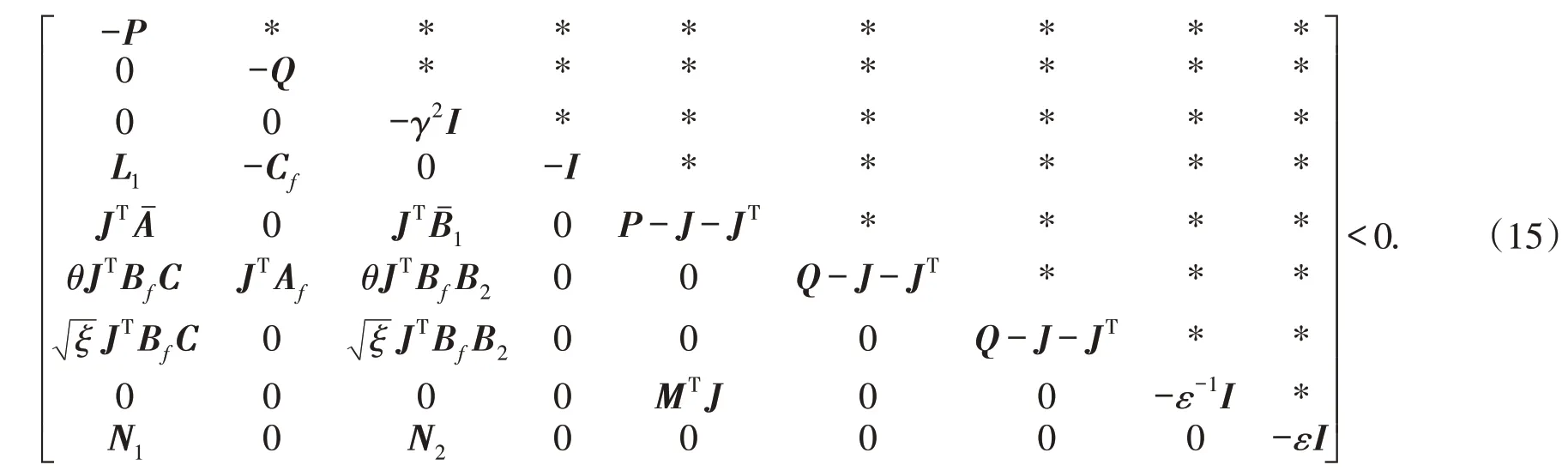
设参数变量U1=JTAf,U2=JTBf,U3=Cf,并代入式(15),化简得式(11),即证明定理2成立.
4 仿真示例
考虑网络控制系统,参数如下:
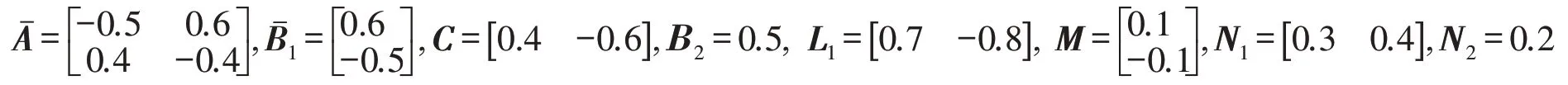
取控制系统的初始状态x(0)=[0.5-0.6]T,滤波器的初始状态xf(0)=[ 0 0 ]T,扰动信号w(k)=2e-0.5ksin(0.5πk),γ=1,丢包率θˉ=0.1,求得方差=0.3.运用Matlab 线性矩阵不等式工具箱计算不等式(11),求得H∞滤波器参数矩阵可行解为:

图1及图2为控制系统状态数据真实值x1(k)/x2(k)与滤波器状态数据估计值x1f(k)/x2f(k)的响应曲线图,从图1及图2可以发现:在离散采样次数较少时,滤波器估计值与控制系统的真实值存在一定的差值,随着离散采样次数的增加差值逐步降低,并趋于吻合,得出滤波误差系统是随机稳定的.图3为控制系统的估计数据z(k)和滤波器的输出数据zf(k)的响应曲线图,图4为滤波误差e(k)的响应曲线图,从图3及图4可以发现:在扰动信号输入下,滤波器的输出数据zf(k)较好地跟踪控制系统估计数据z(k),滤波误差e(k)最终收敛为零,得出滤波误差系统满足H∞性能指标.
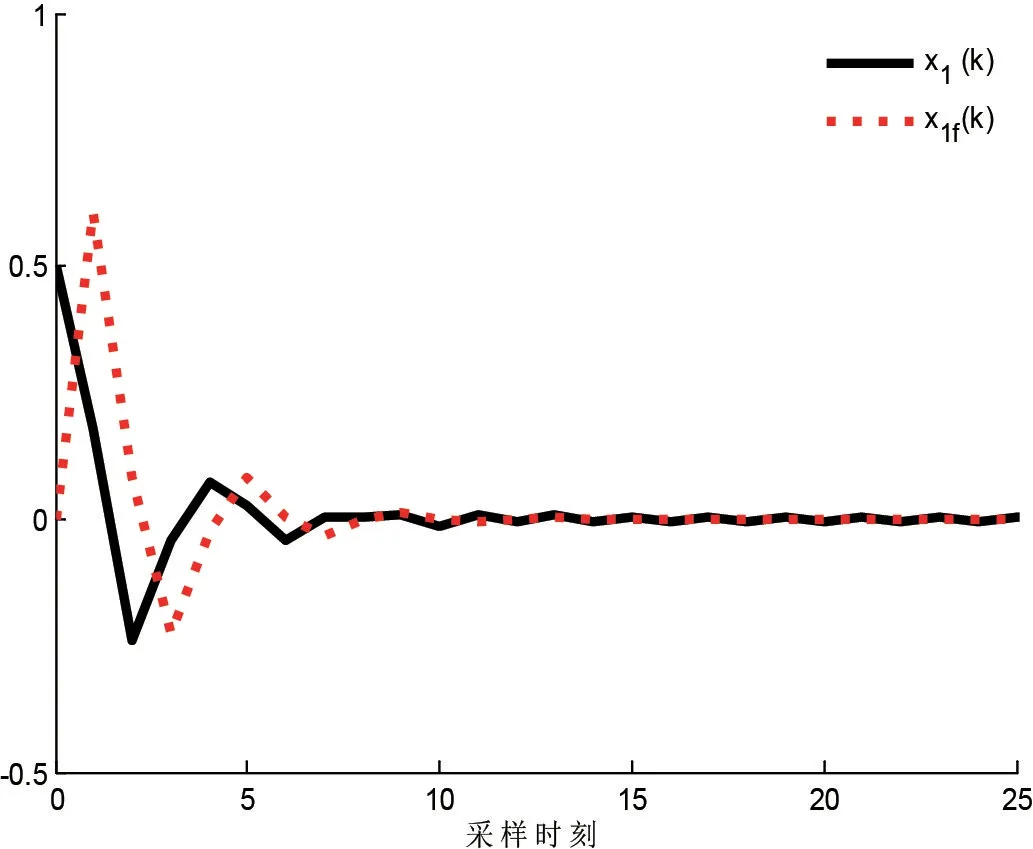
图1 真实值x1(k)与估计值x1f(k)
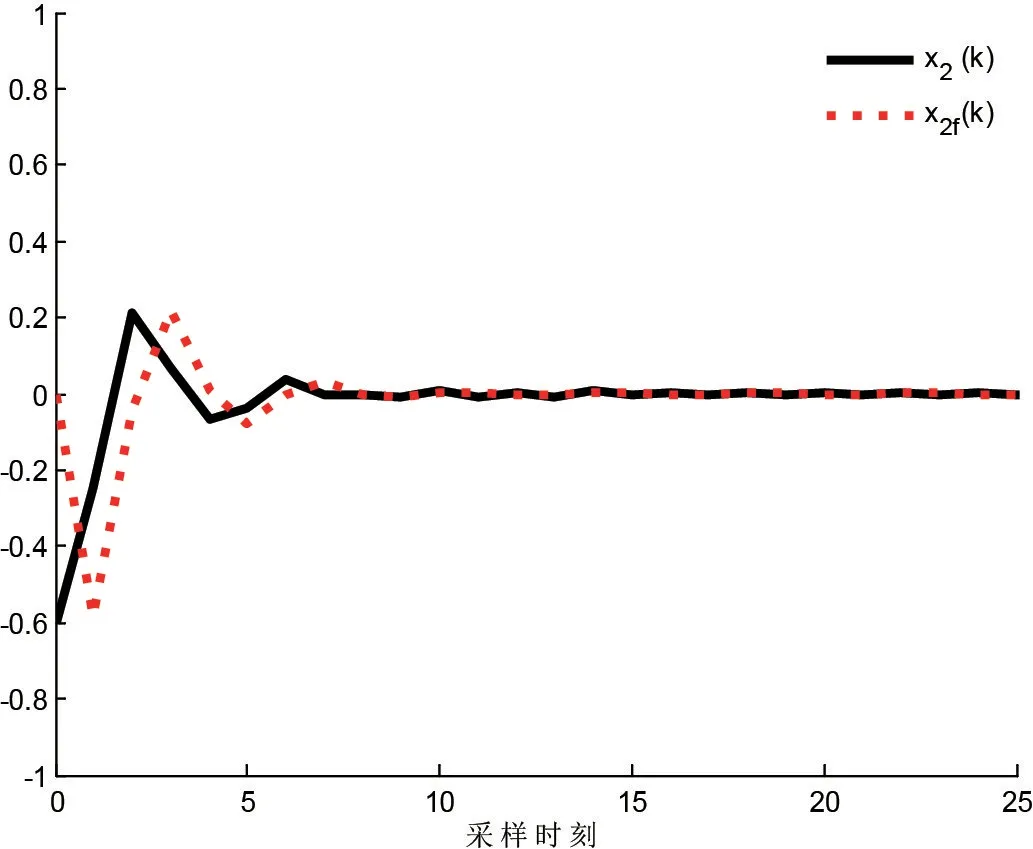
图2 真实值x2(k)与估计值x2f(k)

图3 估计数据z(k)与输出数据zf(k)
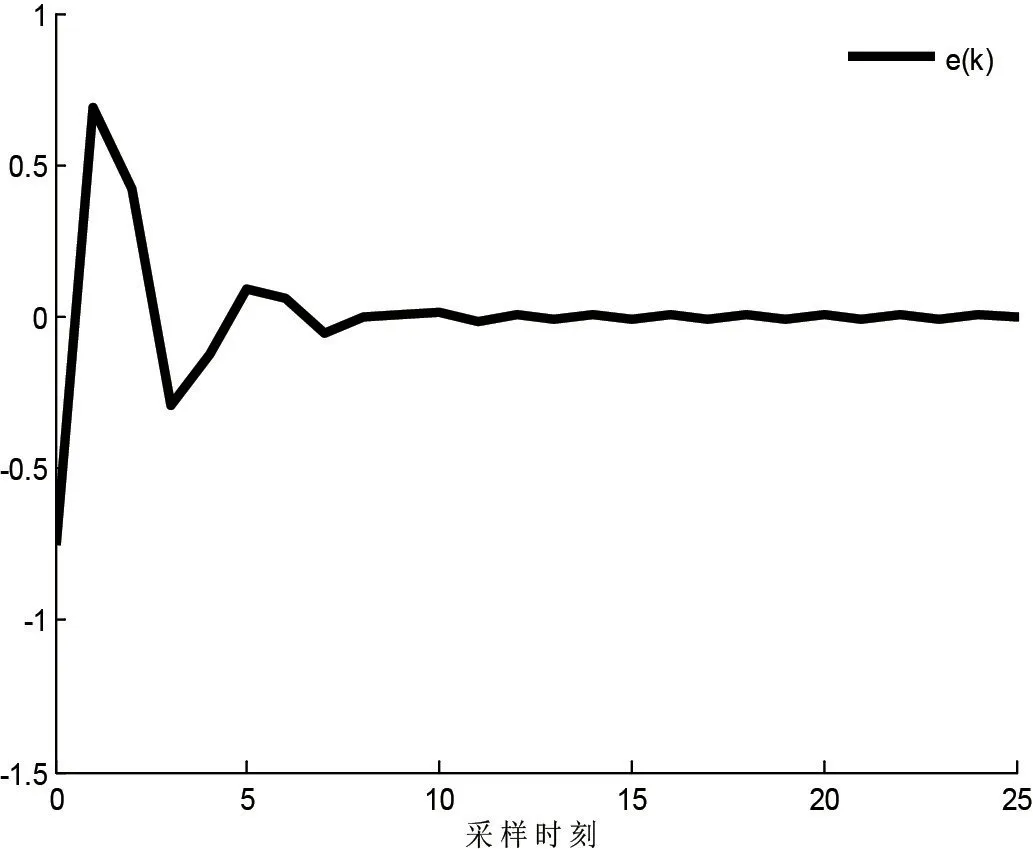
图4 滤波误差e(k)
5 结论
分析一类测量数据存在随机丢失不确定的网络控制系统H∞滤波器设计问题,引入随机伯努利序列构建随机丢包数学模型,运用变量分解法分离不确定参数.运用线性矩阵不等式方法推导出H∞性能指标与丢包率之间定量判据.最后,仿真示例阐述所设计的H∞滤波器输出数据较好地跟踪控制系统估计数据,具有H∞性能指标,为下一步探究大规模复杂网络控制系统提供参考.
