一类轨迹问题,从位似变换说起

广东省东莞市万江教育管理中心(523053) 温河山

位似变换是一种是放大或缩小物体的特殊相似,缩放因子在所有方向上都作相同的变换.如图1,以点O为位似中心,将线段AB进行位似变换,使新图形A′B′与原图形AB的位似比为即如图2,点P在AB上,连接并延长PO,交A′B′于P′,易证ΔA′OP′∽ΔAOP,AP与A′P′仍然是位似关系,且有

图1

结论一在位似变换中,某一点运动时,对应点的运动轨迹与该点的运动轨迹形状相同,只是大小不一定相同.

特殊地,当该点作直线运动时,对应点亦作直线运动.如图2,当点P在线段上从点A运动到点B时,对应点P′的运动轨迹为线段A′B′,运动方向是从点A′到点B′的方向.

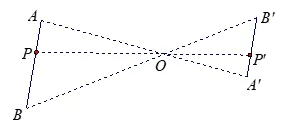
图2

在图2的基础上,将ΔOA′B′绕点O旋转某一度数得到ΔOA′′B′′,点P′相应地旋转到P′′的位置.如图3,连接AA′′、BB′′、CC′′,由∠A′OA′′=∠B′OB′′=∠P′OP′′得到∠AOA′′=∠BOB′′=∠POP′′,所以ΔAOA′′∽ΔBOB′′∽ΔPOP′′.我们不妨称这种变换为类位似变换,其旋转中心点O为类位似中心,称点P和点P′′为对应点,AB和A′′B′′为对应边,新图形与原图形对应边的比为类位似比,称类位似中心与对应点的夹角为类位似角.类位似变换的特点是保持对应边的比例关系不变,类位似角相等.类位似变换是位似变换与旋转变换的合体.

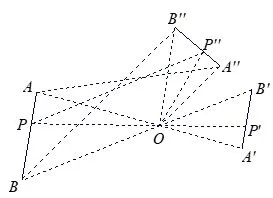
图3

结论二在类位似变换中,某一点运动的过程中,该点与类位似中心连线扫过的图形与其对应点与类位似中心连线扫过的图形相似.

特征分析类位似变换的特征为定角、定比、定中心.运动过程中,类位似角保持不变,比例关系保持不变,类位似中心保持不变,简称为“三定”.

例1如图4,点P以点O为类位似中心作类位似变换,类位似比为已知点P所经过的轨迹长为5,求对应点P′的轨迹长.

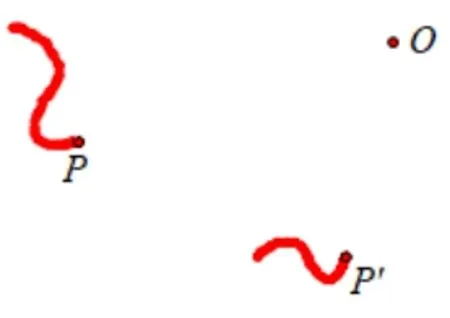
图4

简析点P所经过的轨迹长为5,∴对应点P′的轨迹长为

评析该例运用“三定”性质,直接解题.

例2如图5,正方形ABCD的边长为2,动点B′从点B出发,沿边BA向终点A运动,以CB′为边向上作正方形B′CD′A′.

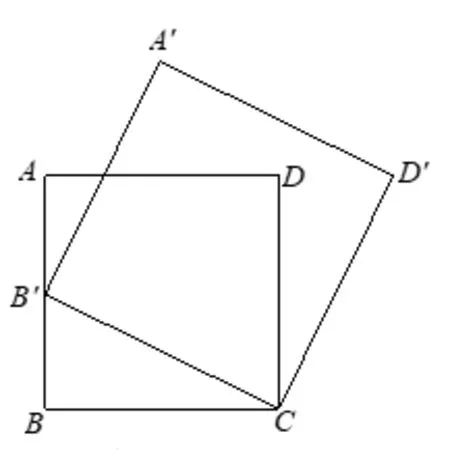
图5

(1)求运动过程中点A′经过的路径长.

(2)求运动过程中DA′的最小值.

(3)求运动过程中CA′扫过的面积.

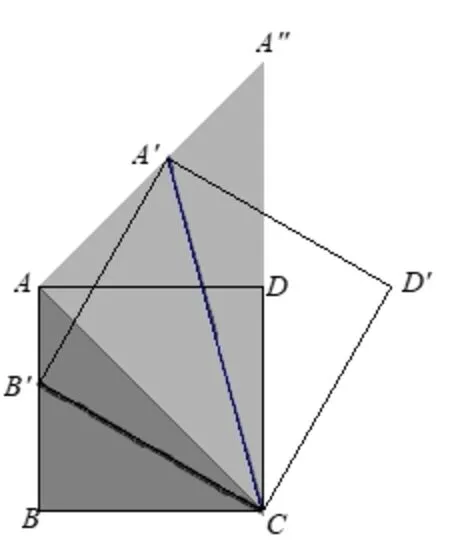
图6

简析(1)变换过程中保持∠B′CA′=45°不变,保持不变,类位似中心为点O,满足“三定”法则,属于类位似变换.过点A作A′′A ⊥AC,垂足为A,延长CD,交A′′A于点A′′.则有点A′的运动经过的路径长

(2)运动过程中DA′的最小值为点D到AA′′的距离,值为

(3)运动过程中CA′扫过的面积为

评析该类位似变换隐藏在以正方形为背景的问题中,由于问题动点在线段上运动,其对应点的运动轨迹也是一条线段,通过动点的起点找到对应点的起点,再通过动点的终点找到对应点的终点,连接对应点的起点和终点即得到对应点的运动轨迹,从而清晰地还原运动过程.

例3(1)如图7,点O为坐标原点,⊙O的半径为1,点A(2,0).动点B在⊙O上,连结AB,向上作等边ΔBAC,求OC的最大值.

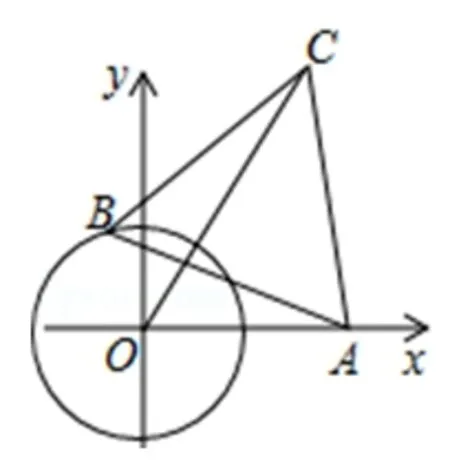
图7

(2)如图8,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.

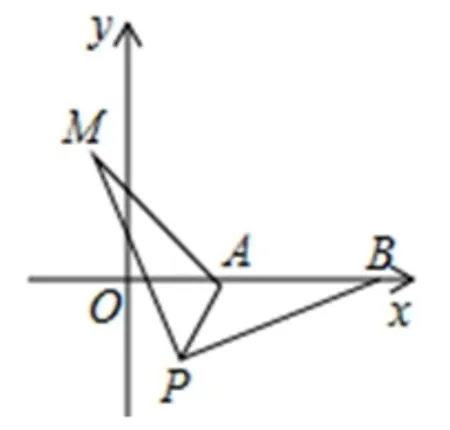
图8

简析(1)如图9,问题符合“三定”原则,属于类位似变换问题.类位似比为1.点C的运动轨迹是圆,其圆心O′是点O的对应点,求得其坐标为O′(1,),故OC的最大值为3.实际上,OC的最小值为1.

图9

(2)如图10,问题(2)是(1)的变式.点B是类位似变换中心,类位似比=点P运动轨迹⊙A的半径为2,对应图形⊙A′的圆心A′是点A的对应点,坐标为(2,3),半径为故AM的最大值为+3.如图11,构建一线三等角模型,可得到此时点P的坐标为

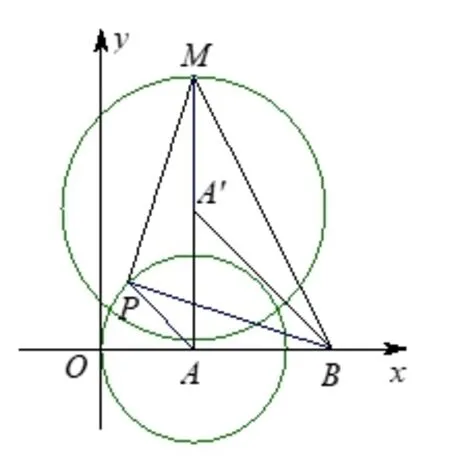
图10

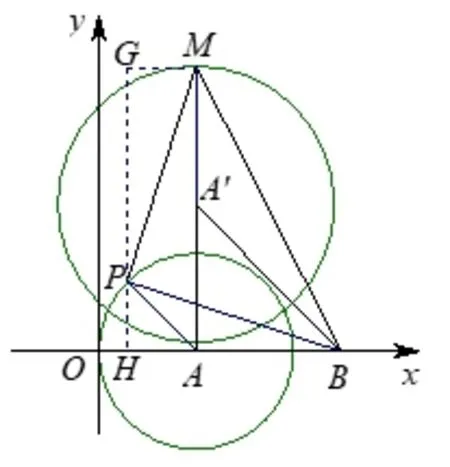
图11

评析该问题中动点运动轨迹为圆,故类位似变换后的轨迹也是圆,可将动点的圆心进行类位似变换得到轨迹的圆心,将动点圆的半径大小乘以位似比即得到轨迹圆的半径大小,从而确定轨迹圆的位置和大小,进而解决问题.

教学反思(1)类位似变换具有“三定”特征,分别是“定角”“定中心”和“定比”;反过来,具有“三定”特征的图形变换就是类位似变换.类位似变换实质上是位似变换和旋转变换的合体,因此同时具有相似和旋转的性质.主要包括图形的形状相同,但大小可能不同(也可能相同).不但如此,某一点在运动变化过程中,该点与类位似中心连线扫过的图形与其对应点与类位似中心连线扫过的图形相似.

(2)组合思维把多项貌似不相关的事物通过想像加以连接,从而使之变成彼此不可分割的新的整体,往往可以得到意想不到的结果.组合是一种创新,使得组合之后的事物“整体具有单个事物所不具备的新质”,增加了新的功能.在数学教学中也常可见此类思维.比如菱形和矩形组合成正方形,平行线与角平分线组合成等腰三角形模型等等.而通过原事物的性质研究往往就可以轻松地研究组合事物的性质.