例谈函数零点问题中的“找点”方法
——一节函数零点问题研究课纪要
2022-06-17北京市第一七一中学100013王桢宇
北京市第一七一中学(100013) 王桢宇
导数在高考数学试题中占有重要地位,也是对于学生“数学运算”素养考查的重要载体,本文旨在通过一道北京高考模拟试题,探讨突出“数学运算”的课堂设计,尤其是呈现学生对于“找点”问题的多角度思考.
1 试题再现
(2021 朝阳区高三第一学期期末试卷,第20 题)
已知函数f(x)=lnx−(a+2)x+ax2(a ∈R).
(I)当a=0 时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(II)求f(x)的单调区间;
(III)若f(x)恰有两个零点,求实数a的取值范围.
2 参考答案
(I)略(II)略
(III)由(II)可知:
①当a≤0 时,f(x)在内单调递增,在内单调递减,当x=时,f(x) 取得最大值=
(i)当−4 ln 2−4≤a≤0 时,所以f(x)在(0,+∞)上至多有一个零点,不符合题意.
(ii) 当a <−4 ln 2−4 时,因为f(1)=−2<0,f(x) 在内单调递减,所以f(x)在内有唯一零点.因为a <−4 ln 2−4<−e,所以−a >e 且因为=−ln(−a)+1+<1−ln(−a)<1−ln e=0,>0,且f(x)在内单调递增,所以f(x)在内有唯一零点.所以当a <−4 ln 2−4 时,f(x)恰有两个零点.
②当0 ③当a=2 时,f(x)在(0,+∞)上单调递增,所以f(x)在(0,+∞)上至多有一个零点,不符合题意. ④当a >2 时,f(x)在内单调递增,在内单调递减.因为当x=时,f(x)取得极大值所以f(x)在(0,+∞)上至多有一个零点,不符合题意. 综上所述,实数a的取值范围是(−∞,−4 ln 2−4). 本题通过讨论参数范围,判断函数单调性,进而确定零点个数,当a <0 时,函数在单调递增,单调递减,若函数存在两个零点,则需>0,可得a <−4 ln 2−4,在此基础上应用零点存在定理,则需在两个区间,分别找到使函数值为负的点,显然x=1 对应的函数值为负,则本题的难点集中在区间上找点的问题,明确该问题为: 已知函数f(x)=lnx−(a+2)x+ax2(a ∈R),若a<−4 ln 2−4 时,求证:∃x0∈f(x0)<0. 为了引导学生探究不同的运算方案,进行比较和归纳,笔者精心设计,在教学时充分调动学生的积极性,师生进过尝试、否定、证实等探究活动,得到以下解题思路. 方法1(常规数值找点) 方法2(指、对互换找点) 在找点过程中,函数是对数函数时,常借助对数与指数的关系化简,过程如下: 因为a <−4 ln 2−4<−4,所以ea 因为a <—4 且ea ∈所以1−ea+e2a >0,f(ea)=a(1−ea+e2a)−2ea <0,所以∃x0=ea ∈ 方法3(取值范围放缩) 因为x ∈所以通过对其取值范围放缩,重构函数解析式,实现找点目的. 方法3.1因为x ∈且ax2<0,所以 错解举例: 课堂上,问题的解决其实并非一帆风顺,多次经历了错解,反思,修正.在此也举一错解,及其调整过程,还原学生思维变化全貌. 在完成方法3.1 后,同学A 提出了自己的解法,他认为,lnx,ax2两项均为负值,—(a+2)x为正值,方法3.1 去掉了ax2实现放缩,那么能否去掉lnx呢? 经过尝试有了一些想法,所以邀请其板演,过程如下: 因为x ∈且lnx <0,所以f(x)=lnx−(a+2)x+ax2<−(a+2)+ax2. 令−(a+2)+ax2=0,可得x2=当a<−4 ln 2−4<−4 时,所以则令此时大家都发现了问题,找到的点并不在区间内,学生A 也不好意思的说,算出x2是满足区间的,感觉x也该满足,为了抢先发言,没有计算到最后就举手了. 错解分析: 首先有同学怀疑,条件是a <−4 ln 2−4,但同学A 用a <—4 求范围,会不会影响结果,很快大家发现,y=在a <—4 时是递减的函数,a <—4 时则a <−4 ln 2−4 自然也大于继续研究,令g(x)=−(a+2)+ax2,这是一个开口向下的抛物线,图像关于y轴对称且g(0)>0,y轴右侧的零点显然在函数值恒正,不存在使g(x)<0 的点.出现这样的结果,说明我们放缩的尺度没有掌控好,过大了,那么在此基础如何进行调整呢,可以预见的是,需要减小放缩的幅度.经过大家的热烈讨论,学生B 给出了解决方法: 方法3.2因为所以lnx <所以f(x)=lnx−(a+2)x+ax2<−ln 2−(a+2)x+ax2.令g(x)=−ln 2−(a+2)x+ax2,这是一个开口向下的抛物线,对称轴为x=>0,且g(0)=−ln 2<=>0,(a<−4 ln 2−4),使得g(x0)<0,同时f(x0)<0. 方法4(函数关系放缩) 为了简化函数解析式形式,学生提出了构造放缩关系消去二次项ax2的想法,实践如下: 因为x 为了继续消去参数a可以令x0=ea,故f(ea) 方法5(删项放缩) 方法5.1(常规数值找点): 因为ea ∈代入函数g(x) 可得:g(ea)=ln ea−aea=a(1−ea)<0,所以∃x0=ea ∈<0,则f(x0)<0. 方法5.2(不等式放缩找点): 令g(x)=lnx—ax,可以利用众所周知的不等式lnx≤x—1(见人教A 版普通高中教科书94 页练习2[1])得:g(x)=lnx—ax 通过师、生对本题的探索与思维碰撞,越发觉得这是一道难得的锻炼学生思维能力的好题,尤其是在多种不同解法产生原理和思路的过程中,逐渐对导数中的找点问题有了更为深入的认识和感悟.师生共同总结常见找点方法如下: (3)指数与对数运算关系找点: 利用两个恒等式loga ax=x及=x转化 (4)对函数放缩找点: 通常借助ex >x >lnx(x >0),ex >x+1(x ̸=0).(见人教A 版普通高中教科书99 页“综合运用”第12 题)[1]等常见恒不等式进行放缩或分组放缩.或者借助零点存在的区间或一些明显成立的不等式对含x的项进行部分放缩,也可删去部分可以不参与运算的项,简化解析式形式. 导数“找点”计算,涉及到方程、不等式,参数讨论,求导运算、四则运算以及估算等能力,追求本质、简单、自然的解题方法,不仅是课堂教学的重要环节,更是培养“数学运算”核心素养的必由之路,教师教学中要舍得把课堂留给学生,让学生切身感受猜想、失败、修正、成功的历程,让思维擦出闪亮火花,照亮未来的科学之路.3 明确问题,突出本质
4 尊重学生,解法多样
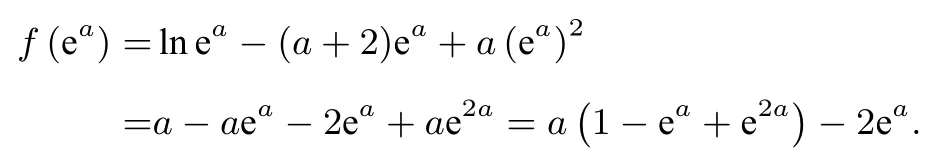
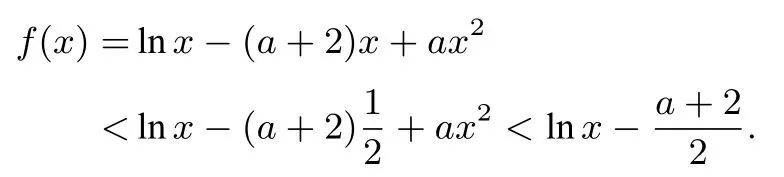
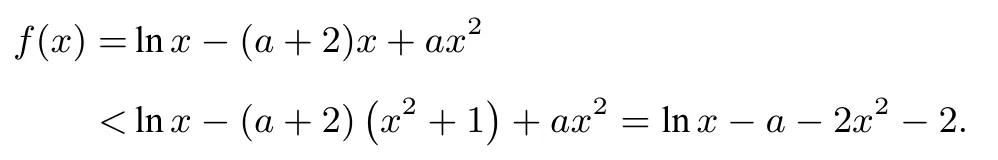
5 反思沉淀,总结提升
