以2021年广东省一道中考题为例——谈对于尖子生初高中衔接的教学

广东省广州市白云广雅实验学校(510430) 袁 宏

2021年广东省中考已经落下帷幕,但是2021年广东省这套数学试题是备受争议的一套试卷,分开每道题目来看,试卷出的不错,考查的知识点比较全面,难度也适中,但是组成一套试题学生感觉就比较难.学生之所以反馈难,本文作者认为主要有两个方面的原因:

第一,中等难度的题目太多,并且整套试题的计算量比较大;第二,考查学生的动手画图能力比较多,方法比较灵活多样,并且省中考时间和广州市中考时间比少了30 分钟.基于这两个原因,学生做不完是常态.本文以23 题为例来介绍题目解法的多样性,并且指出在初三后期的教学中对学有余力的优等生可以安排初高中衔接的内容.

2021年广东省中考试题23 题: 如题23 图,边长为1 的正方形ABCD中,点E为AD的中点,连接BE,将ΔABE沿BE折叠得到ΔFBE,BF交AC于点G,求CG的长.

本题考查的是正方形中的翻折问题中的求线段的长度问题,学生对求线段的长度这类题目在初三后期已经积累了一些方法,例如可以利用勾股定理、三角函数、相似三角形的性质以及等面积法等这些常用的方法来求线段的长度.

认真分析本题题干和观察图形,不难发现题目中有很多的平行线和直角,可以考虑尝试用勾股定理或是相似三角形的性质来求线段CG的长度.但是若是考虑直接用勾股定理来求线段CG的长度,我们要去说明CG在直角三角形中,但是由题意我们不难发现BF与AC是不一定垂直的,所以想用勾股定理直接求线段CG是不太可取.观察图形,不难发现这个图形给我们的感觉是残缺、不完整.我们可以尝试把图形补全,例如延长线段BF,交边CD于一点或是交边AD的延长线于一点,如下图1、图2.

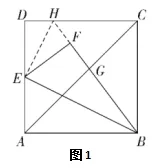
由相似三角形的知识,我们可以利用“X”的三角形相似,利用对应边的比值相等,求出要求的线段CG的长度.若是利用图1来求,需要求出CH的长度,若是利用图2来求,可以求出DM的长度.这两条线段我们都可以根据题意求出来.接下来给出图1的详细解法.

解法一延长线段BF,交边CD于一点H,连接EH,如图1-1.由翻折可得,ΔABE≌ΔFBE,AE=FE,AB=FB,∠EFB=∠EAB=90°,∠AEB=∠FEB,又 ∵E为AD的中点,∴DE=AE=FE,又∵∠EFH=∠EDH=90°,∴在RtΔEDH和RtΔEFH中,∴RtΔEDH≌RtΔEFH(HL),∠DEH=∠FEH,又∵∠DEA=180°,∴∠HEB=90°,∠DEH+∠AEB=90°,又∵∠DEH+∠DHE=90°,∴∠AEB=∠DHE,∴RtΔEDH∽RtΔEAB,∴又 ∵DA=又∵四边形ABCD是正方形,AD=1,∴AC=CD//AB,∴ΔCHG∽ΔABG,又∵AG=AC−CG=

本题目要求线段CG的长度,认真观察图形,不难发现点G是直线AC和直线BF的交点,若我们能够求出这两条直线的解析式,点G的坐标就很容易求出,这样线段CG的长度也就求出来了.而要想求两条直线的解析式,我们就要建立适当的平面直角坐标系,根据条件求出直线解析式,然后再联立解析式把点G的坐标求出即可.所以接下来我们给出解本题的另一种方法,即建系求交点的方法.

解法二以点A为坐标原点,分别以AB,AD所在直线为x轴和y轴建立图3所示平面直角坐标系.此时三点C,B,E坐标分别为C(1,1),同时易得直线AC的解析式为:lAC:y=x,由正切值的二倍角公式可得,又∵tan ∠ABM=

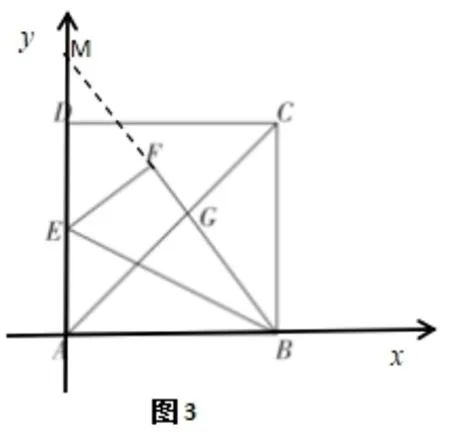
设直线BF的解析式为:lBF:y=kx+将点B(1,0)代入直线BF的解析式中,得,联立两直线的解析式,解得∴交点又∵四边形ABCD是正方形,AD=1,∴∠BAC=45°,

对比以上两种解法,可以看到,利用建系的方法来求点坐标是比较容易想到并且也是比较容易求的,但是在这种方法中唯一一个知识点,二倍角的正切值这个知识点是学生要熟悉的,否则利用建系这种方法来解此题还是有些困难.所以本人认为在初三平时的教学中可以给学生拓展渗透一些高中知识,尤其是在后期复习阶段可以让学生熟练高中的一些结论,对于中考时可以借助高中的知识来解决一些题目是非常快捷简便.

据笔者多年带毕业班的体会,多总结一些可以用到的高中的常用的知识,在平时教学中给学生拓展,有些是可以不必深究道理,可以直接告诉学生结论,让他们在平时的学习中慢慢渗透,学会熟练应用.一些常用的知识点列举如下:

1、两点间的距离公式:已知两点A(x1,y1),B(x2,y2),则线段AB的长度为:

此结论可以在学生学习勾股定理一章时给学生拓展补充,学生比较容易理解和接受,并且这一结论在初中阶段的学习中也会经常用到.

2、中点的坐标公式:已知两点A(x1,y1),B(x2,y2),点C是线段AB的中点,则点C的坐标为

这一结论可以在学习平面直角坐标这一章节知识时给出补充,通过列举具体的实例,学生是容易得到这一结论,并且也容易理解和记忆.并且这一结论在后期与中点有关的问题时都可以用上.

在一次函数这一章中,也有一些非常实用的知识可以给学生拓展.

3、两直线平行时满足的条件: 已知两条直线l1:y=k1x+b1,l2:y=k2x+b2,当l1//l2时,则有k1=k2.

4、若上述两直线互相垂直时,可以得到k1·k2=−1.

这两个知识点在学习一次函数这章时可以给学生拓展补充,在后期的综合题目中可以选择用这两个知识点来解决,非常快捷.

例如,2019年梧州的一道考题:直线y=3x+1 向下平移2 个单位长度,所得直线的解析式是( )

A.y=3x+3 B.y=3x−2

C.y=3x+2 D.y=3x−1

本题我们利用知识点3 很容易得到平移之后的直线的k=3,直接设出平移之后的直线的解析式为:y=3x+b,然后再选择一个特殊点如(0,1)向下平移2 个单位后对应点为(0,−1),将这个对应点带入所设的解析式中,就可以求出b=−1,所以本题的答案很容易就得到是D.若是不用知识点3 我们常规解法用待定系数法,要设两个系数,并且要选两个点带入求出两个系数,增加了计算量,本题只是一道选择题,可以直接用高中的一些结论性的知识点来解决,非常快捷方便.

5、这个知识点是前面我们用过的三角函数正切值的二倍角公式的一般形式,两个角的和或差的正切.不过在初中阶段我们给出的角度都是在锐角的范围.若已知两个锐角,∠A,∠B,则tan(∠A±∠B)=

这两个公式用处我们可以通过上面的一题的第二种解法可以感受到,非常有用.在求一些特殊角的正切值时也是非常方便的.

如可以利用上述公式求tan 15°,tan 75°.

分析可得，

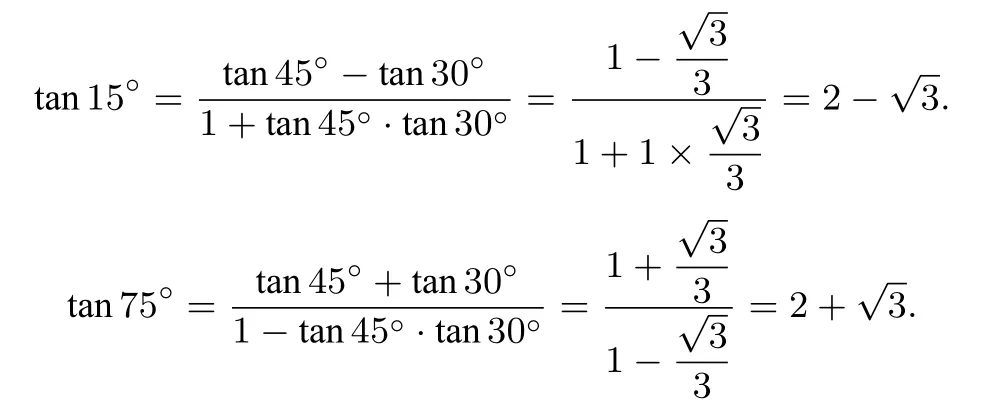
6、点到直线的距离公式: 已知直线l的解析式为:y=kx+b,可变形为kx−y+b=0,或是更一般的表达形式:Ax+By+C=0(A,B,C为常数).直线外一点P(a,b),则点P到直线l的距离为:d=

7、初中阶段学习的勾股定理的推广: 余弦定理.对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积,若三边为a,b,c三角为A,B,C,则有以下结论:a2=b2+c2−2bccosA或b2=a2+c2−2accosB或c2=b2+a2−2bacosC.

8、正弦定理: 在任意一个三角形中,各边和它所对角的正弦值的比相等且等于这个三角形外接圆的直径.即:=2r(r为三角形外接圆的半径).

这两个定理都是三角形中的两个基本定理,是建立了三角形中的边和角之间的关系,在求三角形的边长或是角度是非常有用的.

除了高中这些常用到的知识点外,对于尖子生我们还可以对他们拓展一些初中被删除掉,不做为必学的知识点.补充学习这些知识点的时候,可以让学生利用已学的知识点给出详细的证明,加深对所学知识的应用,而不至于死记硬背知识点.常用到的有以下圆中的一些知识点:

9、证明四点共圆的结论:在一个四边形中,若满足四边形的对角互补,则一定可以得到四边形的四个顶点在同一个圆上.

还有圆幂定理:相交弦定理、切割线定理、割线定理、弦切角定理四个常用定理.

10、相交弦定理:若圆内任意弦AB、弦CD交于点P,则PA·PB=PC·PD;

11、切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项;

12、割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等;

13、弦切角定理:圆的切线与圆相交的弦相交所形成的夹角称为弦切角,弦切角的度数等于它所夹的弧所对的圆心角度数的一半,等于它所夹的弧所对的圆周角的度数.

以上的四个定理是圆幂定理的四个结论,也是比较常用的几个结论,可以用一节课的时间让学生来学习推导一下,拓展学生的视野,开阔学生的思路.

除了以上的几个常用的知识点外,还有一些常用的解题方法,如建立平面直角坐标系解决一些几何问题或是代数综合性的题目,平时的教学中也需要给学生渗透一些.这样学生在步入高中学习时就不会感觉那些知识很突兀,慢慢感受到高中学习是在进一步加深知识点的学习,不会认为数学是一门很难学的学科,从心理上可以接受它,从而摆脱了学习数学的恐惧心理.