立足基本图形 积累活动经验 发展核心素养——2021年重庆市中考压轴题第26题的探索

广东省广州市第二中学(510530) 代本富

1 题目呈现

(2021年重庆中考数学第26 题) 在ΔABC中,AB=AC,D是边BC上一动点,连接AD,将AD绕点A逆时针旋转至AE的位置,使得∠DAE+∠BAC=180°.

(1)如图1,当∠BAC=90°时,连接BE,交AC于点F,若BE平分∠ABC,BD=2,求AF的长;

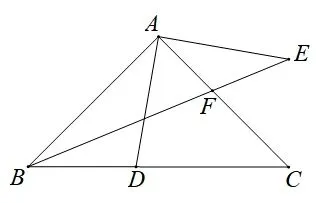
图1

(2)如图2,连接BE,取BE的中点G,连接AG,猜想AG与CD存在的数量关系,并证明你的猜想;

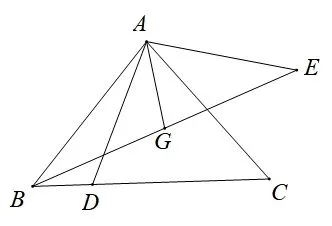
图2

(3)如图3,在(2)的条件下,连接DG,CE,若∠BAC=120°,当BD >CD,∠AEC=150°时,请直接写出的值.

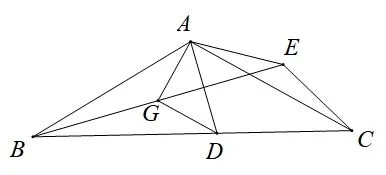
图3

2 试题评析

本题是以几何变换(旋转)为背景的中考压轴题,将一些常见的基本图形结构叠加,考查全等三角形的判定和性质,等边三角形的判定和性质,相似三角形的判定和性质,解三角形等知识,涉及的知识面广,要求学生积累丰富而有效的数学活动经验,才能识别基本图形,合理添加辅助线,明确解题思路,从而进行逻辑推理和运算.考查学生推理能力、模型思想、几何直观、运算能力等基本素养.本题视角众多,解法多样,不同层面的学生都可以尝试求解,符合课程标准和教材对核心知识的教学要求,有利于有效评价和引领教学.

本题三个问题设置环环相扣,层层递进,从一个特殊状态求值,到一般位置探究变化中的不变关系,最后再给一些特殊条件,导边导角,挖掘丰富的基本图形结构,利用计算进行推理.

第(1)问是一个特殊状态,蕴含角平分线、“手拉手”等常见的基本图形结构,可利用全等或相似解决问题.

第(2)问是共顶角顶点且顶角互补的两个等腰三角形结构,关键条件是中点,可利用中点条件由因导果,也可利用几何直观猜出两倍关系,执果索因,由基本活动经验利用中点问题常见处理策略(如倍长中线、构造中位线等)来解决.

第(3)问把前两问的结论综合在一起,使得题目中出现的线段和角都具有特殊性,且蕴含丰富的基本图形,例如由等边ΔADE,可考虑构造手拉手全等;由∠ABC+∠AEC=180°,识别出“对角互补”四边形基本图形,可考虑构造辅助圆导边导角.

3 解法荟萃

基于以上对图形结构的分析,下面给出每个小问的几种构图破题思路:

(1)思路1(“手拉手”+“角平分线”): 如图4,过点F作FH⊥BC于点H,易证ΔABD≌ΔACE(SAS),则CE=BD=2,∠ACE=∠ABD=45°,所以∠BCE=90°,由BE平分∠ABC得∠1=∠2,AF=HF,又由∠1+∠5=∠2+∠3=90°,得∠3=∠5=∠4,所以CF=CE=2,AF=FH=

图4

思路2同上可证CE=BD=2,∠BCE=90°,可得FH//EC,则设FH=x,则由得解得

思路3(“手拉手”+相似): 如图5,同上可证CE=BD=2,∠1=∠2,∠BAF=∠BCE=90°,则所以故

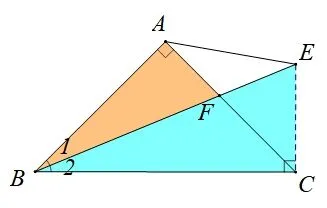
图5

评析本题直接计算AF长度的条件不够,立足基本图形分析,首先利用一个常见的“手拉手”全等结构导边导角,得到CE=2 及∠BCE=90°,然后思路1 利用角度发现CF=CE=2 是关键;思路2 直接从计算的角度去思考;思路3 结合角平分线,识别一个基本的相似三角形,求得目标.

(2)思路1(倍长中线): 如图6,延长AG至点M,使GM=AG,连接EM,易证ΔABG≌ΔMEG(SAS),则EM=AB=AC且AB//EM,所以∠AEM+∠BAE=180°;又由∠DAE+∠BAC=180°,可得∠DAC+∠BAE=180°,故∠AEM=∠DAC,可证ΔDAC≌ΔAEM(SAS),所以CD=MA=2AG.

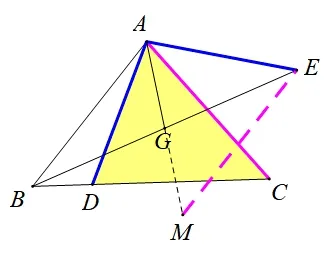
图6

思路2同理,如图7,延长AG至点M,使GM=AG,连接BM,证ΔDAC≌ΔMBA(SAS)也可.

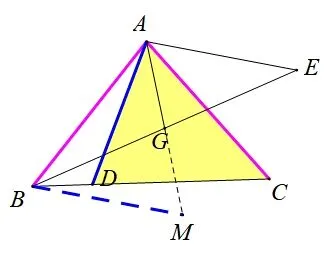
图7

思路3(加倍→构造中位线): 如图8,延长BA至点M,使AM=AB,连接EM,同上由∠DAE+∠BAC=180°,可得∠DAC+∠BAE=180°,故∠DAC=∠EAM,可证ΔDAC≌ΔEAM(SAS),所以CD=EM=2AG.

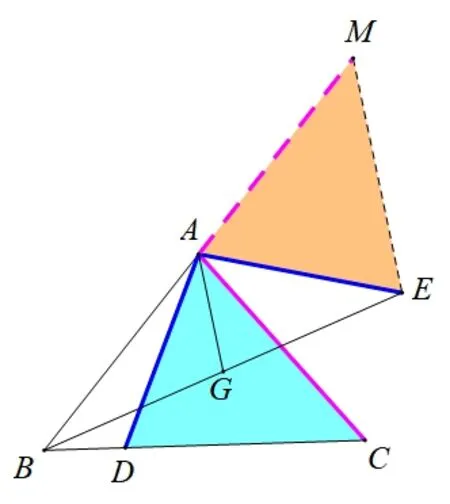
图8

思路4同理,如图9,延长EA至点M,使AM=AE,证ΔDACΔMAB(SAS)也可.

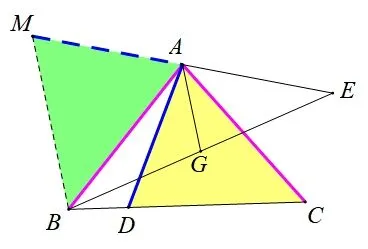
图9

思路5(加倍→构造中位线): 如图10,延长DA至点M,使AM=AD,连接CM,取CM中点N,连接AN,同上由∠DAE+∠BAC=180°,可得∠DAC+∠BAE=180°,由∠DAC+∠MAC=180°,故∠BAE=∠CAM,可证ΔBAE≌ΔCAM(SAS),所以CD=2AN=2AG.

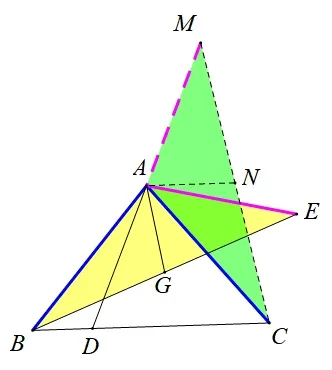
图10

思路6同理,如图11,延长CA至点M,使AM=AC,连接DM,AM,取DM中点N,连接AN,同上由∠DAE+∠BAC=180°,可得∠DAC+∠BAE=180°,由∠DAC+∠MAD=180°,故∠BAE=∠MAD,可证ΔBAE≌ΔMAD(SAS),所以CD=2AN=2AG.

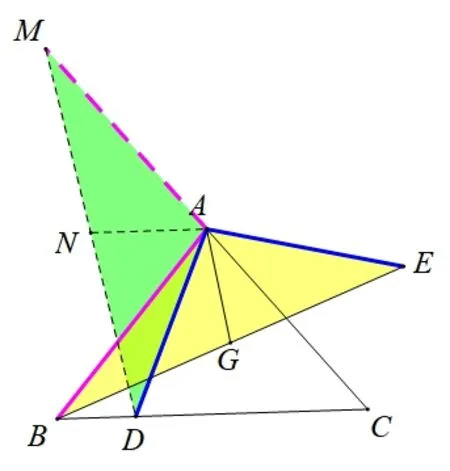
图11

思路7(半分→构造中位线): 如图12,取AB中点M,连接MG,同上由∠DAE+∠BAC=180°,可得∠DAC+∠BAE=180°,又由中位线易证∠GMA+∠BAE=180°,AE=2MG,则∠GMA=∠DAC,由可证ΔGMA∽ΔDAC,所以即所以CD=2AG.

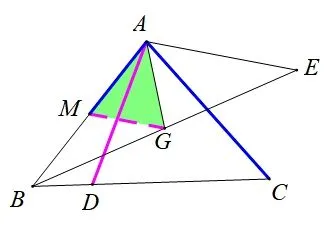
图12

思路8同理,如图13,取AE中点M,连接MG,同上由∠DAE+∠BAC=180°,可得∠DAC+∠BAE=180°,又由中位线易证∠GMA+∠BAE=180°,AB=2MG,则∠GMA=∠DAC,由可证ΔGMA∽ΔCAD,所以,即所以CD=2AG.

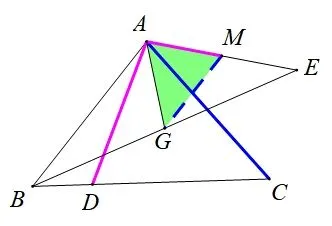
图13

思路9(半分→倍长中线): 如图14,取CD中点N,连接AN并延长至点M,使NM=AN,连接DM,易证ΔANC≌ΔMND(SAS),则DM=AC=AB且DM//AC,所以∠ADM+∠DAC=180°;又由∠DAE+∠BAC=180°,可得∠DAC+∠BAE=180°,故∠ADM=∠BAE,可证ΔADM≌ΔEAB(SAS),所以CD=2DN=2AG.

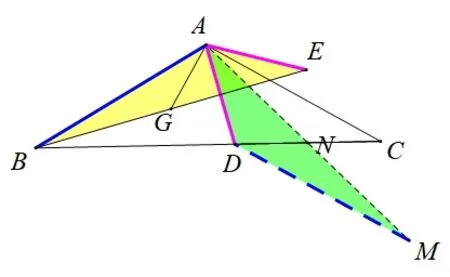
图14

思路10同理,如图15,取CD中点N,连接AN并延长至点M,使NM=AN,连接CM,证ΔEABΔMCA(SAS)也可.

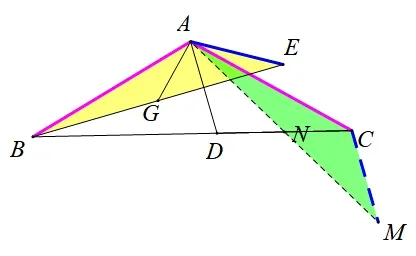
图15

评析上述解法异曲同工,首先都需要将条件“∠DAE+∠BAC=180°”转换为“∠DAC+∠BAE=180°”,再利用线段两倍关系以及中点常见的处理策略(即倍长中线或构造中位线等)积极构造全等.事实上,不管取哪条线段的中点(或倍长)本题都能得以解决,不同层面的学生都可以尝试求解.立足基本图形分析,在复杂多变的几何图形中,关键是会识图,能构图,这需要平时积累丰富的基本图形结构以及基本的活动经验,能做到“慧眼识珠”,善于寻找或构造常见的基本图形.

(3)思路1(“手拉手”): 如图16,延长BA至点M,使AM=AB,连接EM,CM,DE,因为∠BAC=120°,所以∠DAE=∠EAM=60°,则ΔACM、ΔAED均为等边三角形,由(1)可证得ΔDAC≌ΔEAM(SAS),所以∠AME=ACD=30°,则ME平分∠AMC,所以ME垂直平分AC,故CE=AE=DE,所以∠EAC=∠ECA=15°,所以∠CAD=∠EAM=45°,所以∠BAD=∠ADB=75°,所以BA=BD,所以BE垂直平分AD,所以DG=AG=设DG=x,则CD=2x,如图17 解ΔADC可得,BD=BA=故

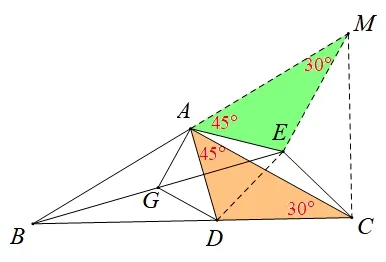
图16

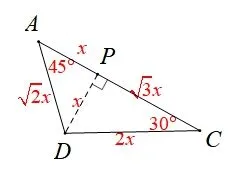
图17

思路2(辅助圆): 如图18,由∠ABC+∠AEC=180°,可知A,B,C,E四点共圆,所以∠AEB=∠ACB=30°,同上可证ΔAED为等边三角形,所以∠DEB=∠AEB=30°,所以BE垂直平分AD,所以BA=BD,DG=AG=∠ACE=∠ABE=∠CBE=∠CAE=15°,∠CAD=45°,设DG=x,则CD=2x,如图17 解ΔADC可得,BD=BA=AC=故

图18

评析该问图形结构蕴含丰富,思路1 构造一个等边三角形ΔACM,与已有等边三角形组成“手拉手”全等结构,然后导边导角,推导出系列基本图形结构,如顶角为150°的等腰ΔAEC、顶角为30°的等腰ΔABD、等腰RtΔCDE、等腰RtΔAGD、以及含特殊角的ΔACD等,然后主动设元,表示相关线段长,从而获解;思路2 需识别“四点共圆”结构,利用辅助圆导边导角,从而发现一些基本的图形结构,然后解ΔACD求得相关线段长.本题题目中出现的线段和角都具有特殊性,所以无论最后是解ΔACD,ΔABC,ΔAEC或其他均可获解,解法众多,有兴趣的读者可自行尝试.以上解法最后落脚的基本图形是一致的,即一题多解,多解归一,是利于发展学生核心素养的.

4 解题感悟

《义务教育数学课程标准(2011 版)》指出:“数学活动经验的积累是提高学生数学素养的重要标志.帮助学生积累数学活动经验是数学教学的重要目标,是学生不断经历、体验各种数学活动过程的结果”[1].2021年重庆市中考压轴题第26 题的三个问题设置环环相扣,层层递进,是一道凸显数学核心素养的试题.完整解答本题需要学生真正理解数学知识,积累丰富而有效的数学活动经验.

几何压轴题图形本身可能是复杂的,多变的,也可能是“不完整”的,多角度分析题目背景,把握应用题目条件,结合图形进行分析是破题关键.在日常教学中,需要师生共同归纳总结常见的几何模型,但又不能拘泥于模型,要引导学生读图,识图,最终能构图,引导学生通过对基本图形结构的分析,深刻理解模型的关键条件,透析数学问题的本质,这有助于学生遇见图形展开丰富的模型联想,从而主动的去构建模型,让所添辅助线更具目的性.更好的感悟背后所蕴含的数学思想,知道如何应用到其他情境中去,发展学生数学核心素养.

另外教学过程中应有意识的选择一些经典的,复杂的,具有代表性的几何图形,以此引导学生自己总结提炼出一些反复出现的,经典的,应用广泛的基本图形结构,并应用基本图形分析法,帮助学生更好的探索解决问题的思路,猜想结果,发展学生的直观想象素养;培养学生从复杂的图形中分离出基本图形的能力,强化数学建模意识,让学生学会把陌生的、复杂的问题化归为熟悉的、简单的问题,这也正是培养学生数学学科核心素养的关键所在.