微尺度下H形分布流道充模流动不平衡特性

2022-06-16安晓玉杨朝龙

高分子材料科学与工程 2022年3期

徐斌，杨波，安晓玉，杨朝龙

(1. 西南科技大学制造过程测试术教育部重点实验室，四川绵阳 621010；2. 中车唐山有限责任公司，河北唐山 063000 )

随着微纳米技术的快速发展，作为微/纳制造领域的研究前沿和热点，微注塑成型技术已取得了显著的进步，主要集中在模具设计、成型工艺以及聚合物熔体的流动特性等方面[1,2]。相对于传统注塑制品，微注塑制品与流道凝料的质量之比大幅减小，高效化和精密化的工业生产迫切要求采用一模多腔注塑成型。

一模多腔注塑成型时，流道虽然对称布置，但容易出现充填不平衡，会对制品的质量、尺寸和性能等产生重要影响，导致制品品质不一致。研究表明，注塑充填不平衡的形成机理是对称分布的分流道中熔体的剪切梯度引起剪切摩擦热（黏性耗散热）分布不对称，导致受温度影响的流变分布不对称引起熔体流动速度分布不同[3,4]。微注塑成型的典型特征是高注射速率与高模具温度，而且微尺度效应(Micro scale effects)作用显著[5]。当聚合物熔体进入对称分布的微尺度分流道后，受高注射速率、壁面滑移、表面张力等因素影响，其流变行为发生显著变化。且微尺度对流换热与传统注塑不同，由于表体比显著增大，熔体的热量极易散失，进而改变熔体在流道内的温度、速度和压力分布[6,7]。目前对微注塑充填不平衡已初步开展了实验研究，如：Xu 等[5]开展了微注塑充填不平衡实验，发现注塑充填不平衡随微圆柱特征尺寸而变化，与工艺参数有关，其中模具温度与注射速率对充填不平衡影响明显。并设计了3 种不同形状转角来改善充填不平衡。郭幼丹等[8]对多型腔微注塑成型过程中玻纤增强聚丙烯(GFRPP)熔体在流道中的纤维取向、温度和流动速度偏移现象进行模拟和分析，结果表明，GFRPP 在不同的注射速率下熔体的纤维取向、流动速度、温度分布会产生偏移，导致流道系统和型腔充填不平衡。

目前对影响微尺度流动的关键因素与充填不平衡的形成机理还缺乏深入研究。本文借鉴传统注塑充模流动理论，采用注塑常用的H 形分布一模八腔对称流道，利用数值模拟探究壁面滑移、对流换热及尺度效应这3 种关键因素对充填不平衡的影响规律。

1 数学模型

1.1 熔体充模流动的基本方程

1.1.1 连续性方程：对于微注塑成型熔体充模流

动，其流动形式仍然属于连续介质力学的范畴[9]。根据熔体不可压缩的假设，黏性流体力学的连续方程式可简化为

等式左边第1 项为压力项，第2 项为表面黏性力项。

1.1.3 能量方程：当型腔尺寸降至微米量级时，熔体的流动行为仍然遵循能量守恒定律[9]。设熔体为不可压缩的广义牛顿流体，则能量方程式简化为

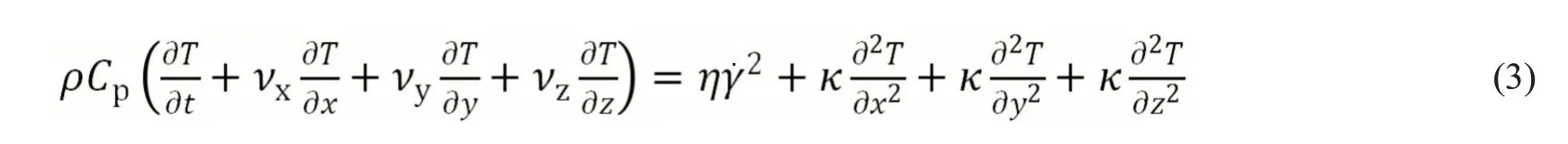
1.2 黏度模型

由于Cross 模型能在较宽的剪切速率范围内准确地表征黏度的变化，因此选用Cross 模型

式中γ——分别为熔体的剪切速率和温度；n——非牛顿指数；η0——零剪切黏度；λ——松弛时间。同时，为了考虑温度对黏度的影响，采用WLF 模型，WLF 表达式为

式中：T*=D2+D3p，A2=A2+D3p。D1，D2，D3，A1，A2为模型常数。选用日本宝理公司生产的M90-44 型聚甲醛(POM)，利用Rosand-RH7 型号双料筒高分辨率毛细管流变仪测得口模直径1000μm下POM 材料的黏度实验数据，其黏度随剪切速率变化曲线如Fig.1。通过Matlab 进行拟合，得到黏度模型参数见Tab.1。M90-44 型POM 材料的参数如Tab.2。

Tab. 1 Viscosity model coefficient

Tab. 2 Material parameters

Tab.3 Test data of wall slip of POM

Tab. 4 Simulation experiment parameters are set horizontally

Fig.1 Relationship curves between viscosity and shear rate of POM

1.3 壁面滑移

在微注塑过程中，通过大量实验证明[10]，由于吸附-解吸附或缠结-解缠结的存在，壁面滑移对微注塑是不可忽略的。根据聚合物挤出成形加工中的滑移理论，壁面处的熔体滑移速度是切应力的函数。因此，应用Nvaier 滑移定律来描述熔体壁面滑移特性，其表达式为

1.4 熔体与壁面间对流换热

由傅里叶传热定律,垂直流动方向的法向热流密度为

1.5 初始条件与边界条件

2 数值模拟

2.1 几何模型建立及网格划分

完整流道系统如Fig.2(a)。流动不平衡的产生主要发生在分流道中，型腔部分在计算时会产生不收敛，因此对三维模型进行简化，由于对称性，仿真时只保留一半的流道系统，且在注塑过程中，主流道内剪切速率低，熔体温度保持不变，故在仿真时省略主流道。在Workbench 中划分网格，网格单元采用四面体网格，网格数量95804，如Fig.2(b)所示。

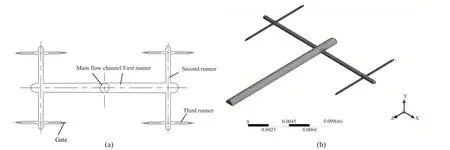
Fig.2 Flow passage system layout and grid division

2.2 单因素实验设计

以单因素法，在考虑壁面滑移、对流换热条件下将Tab.4 中的变量自由组合进行仿真模拟实验。

3 结果与讨论

根据聚合物流变理论，在相同的长径比下，设置3 种尺寸的流道系统。流道系统1：一级分流道直径1000μm，二级分流道直径500μm，三级分流道直径250μm；流道系统2：一级分流道直径500μm，二级分流道直径250μm，三级分流道直径125μm；流道系统3：一级分流道直径350μm，二级分流道直径175μm，三级分流道直径87.5μm。各流道长径比均为16。设置边界条件和材料参数，仿真结果如Fig.3 所示。从图中可以看出，从主流道到浇口，由于剪切摩擦的作用，流道表面熔体的温度逐渐升高，在浇口处熔温达到最大值。浇口处熔体温度变化最明显，在同一侧二级分流道上对称分布的2 个分流道距浇口100μm处取截面，温度分布如Fig.3(b)和Fig.3(c)所示。从图中可以看出，截面处出现了左右温度分布不对称现象，分流道中心处温度较低，越靠近壁面温度越高，且相对称截面温度分布不一致。由于2 个截面对称点上温度差变化规律相同，现以流道内侧点1、2 温度差作为充填不平衡的评价指标。

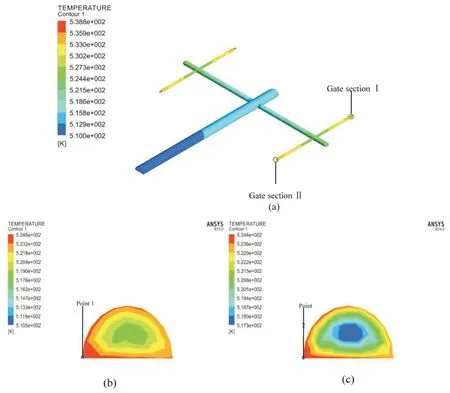
Fig.3 Temperature distribution of the whole runner system and gate section under the insulation boundary

3.1 壁面滑移对充填不平衡的影响

设熔体入口温度为500 K 和510 K 2 种情况，设置绝热、对流换热系数h=1000 W/(m2·K)、对流换热系数h=2500W/(m2·K) 3 种边界条件。统计所有情况下点1 与点2 的温度差，绘制成如Fig.4，Fig.5，Fig.6 曲线图。

从Fig.4，Fig.5，Fig.6 可知，3 种温度边界条件下，随着剪切速率的升高，无壁面滑移与考虑壁面滑移的2 种情况下，对称点间的温度差异总体呈上升趋势，这是因为熔体与壁面剪切摩擦生热，导致流道内熔体温度升高。而在流道尺寸、剪切速率、熔体入口温度相同的情况下，考虑壁面滑移的温差ΔT比不考虑壁面滑移的ΔT小，即壁面滑移能降低流道内对称点间的温度差异。

如Fig.6，在对流换热系数h=2500 W/(m2·K)边界下，当熔体温度为500 K 时，Fig.6(a)中，流道系统1内，考虑壁面滑移时对称点温差(ΔT)的最大值为11.543 K，ΔT的最小值为1.025 K；不考虑壁面滑移时，ΔT的最大值为33.3 5 K，ΔT的最小值为21.341 K。2 种情况下，不考虑壁面滑移的最大温差较考虑壁面滑移时高出21.807 K，最小温差高出20.316 K。流道系统2 内，考虑壁面滑移时，ΔT的最大值为1.326 K，ΔT的最小值为0.783 K；不考虑壁面滑移时，ΔT的最大值为32.36 K，ΔT的最小值为20.428 K。2 种情况下，不考虑壁面滑移的最高温度较考虑壁面滑移时高出31.314 K，最低温度高出19.645 K。流道系统3 内，考虑壁面滑移时，ΔT的最大值为1.176 K，ΔT的最小值为0.537 K；不考虑壁面滑移时，ΔT的最大值为31.98 K，ΔT的最小值为19.037 K。2 种情况下，不考虑壁面滑移的最高温度较考虑壁面滑移时高出30.804 K，最低温度高出18.5 K。当熔体温度为510 K 时，如Fig.6(b)，其变化规律与熔体温度为500 K 时一致。其中Fig.4，Fig.5即绝热边界、对流换热系数h=1000 W/(m2·K)边界中壁面滑移对对称点温度差的影响规律与Fig.6 一致。从以上数据可以看出，壁面滑移能较大程度地降低温度差异，有利于微注塑过程，改善充填不平衡。

根据已有的研究发现，在对称分布的模具流道内高速注射时，造成充填不平衡的原因是流道内熔体与壁面产生剪切摩擦热导致熔体温度分布不对称[3,4]。而熔体黏度对温度具有较高敏感度，壁面滑移的加入，使得与壁面接触的熔体其流动速度不再为0，增加了熔体的平均流速，减少了流道内的剪切摩擦热，使熔体的平均温度降低，导致对称点间的温度差减小，因此考虑壁面滑移更加有利于充填平衡。

3.2 壁面滑移条件下流道尺度效应对充填不平衡的影响

在微米级条件下，聚合物熔体具有强烈的尺度效应。熔体的流变特性、黏性耗散作用的强度等都会随流道尺寸的改变而变化。因此在微注塑过程中，考虑熔体的尺度效应是必不可少的。已知考虑壁面滑移有利于充填过程，而在微米量级注塑时，微注塑过程中存在明显的尺度效应，会影响熔体的流动性。因此设计了3 种不同尺寸的流道系统，分别进行仿真分析，探究考虑壁面滑移的同时，流道尺度效应对充填不平衡的影响。统计对称点的温度差如Fig.4，Fig.5，Fig.6。从图中可以看出，尺度效应对对称点间温度差异有着显著的影响，在考虑壁面滑移条件下，从Fig.4(a)，Fig.5(a)，Fig.6(a)可得出，当熔体入口温度为500 K 时。绝热边界条件下，流道系统1，2，3 内的温差ΔT的最大值分别为0.312 K，0.122 K，0.098 K，ΔT的最小值分别为0.081 K，0.077 K，0.072 K；对流换热系数h=1000 W/(m2·K)边界条件下，流道系统1，2，3 内的温差ΔT的最大值分别为25.234 K，4.913 K，3.656 K，ΔT的最小值分别为5.146 K，0.742 K，0.985 K；对流换热系数h=2500W/(m2·K)边界条件下，流道系统1，2，3 内的温差ΔT的最大值分别为11.543 K，1.326 K，1.176 K，ΔT的最小值分别为1.025 K，0.783 K，0.537 K。Fig.4(b)，Fig.5(b)，Fig.6(b)中，熔体温度为510 K 时，其变化规律与熔体温度500 K 时一致。从以上数据可以得出，在考虑壁面滑移的同时，尺度效应会影响流道内对称点间的温度差异，且随着流道尺寸的减小，对称点温差ΔT也在减小，充填不平衡得到改善。

Fig.4 Influence of wall slip on temperature difference at symmetry point under adiabatic boundary conditions

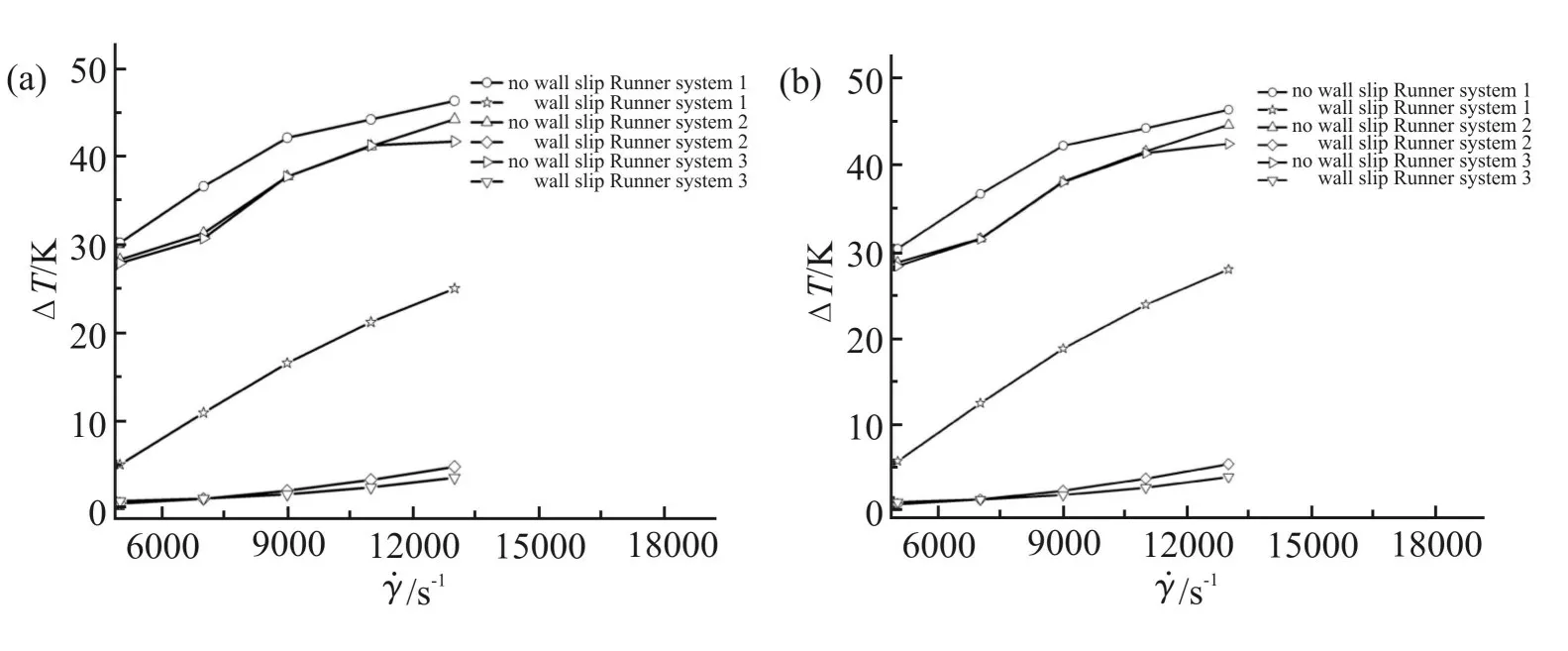
Fig.5 Influence of wall slip on temperature difference at symmetry point under boundary condition of convection coefficient h=1000 W/(m2· K)

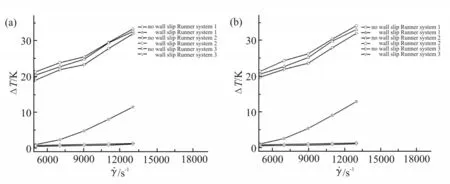
Fig.6 Influence of wall slip on temperature difference at symmetry point under boundary condition of convection coefficient h=2500 W/(m2· K)

这是因为当熔体温度、剪切速率及热边界条件不变的情况下，壁面的剪切应力保持不变，由式(6)可得，壁面滑移速度也不变，但剪切平均速度逐渐减小，此时壁面滑移体积流量与剪切速率体积流量比值随着流道尺寸的减小而增大，表明壁面滑移对流体的流动影响较大。而壁面滑移有利于减小剪切摩擦热，因而对称点间的温度差异越小。即流道尺寸在一定范围内缩小有利于微注塑过程，改善充填不平衡。

3.3 对流换热对充填不平衡的影响

在实际的加工生产中，熔体在注塑过程中与壁面存在对流换热，会导致一部分热量的散失，因此设置熔体温度为500 K，510 K，模具温度为413 K，考虑绝热边界及表面传热系数分别取1000 W/(m2·K)，2500 W/(m2·K)边界。通过比较绝热边界与对流换热边界条件下对称点温升变化来反映对流换热对微注塑充填不平衡的影响。统计单因素试验下的数据得Fig.7，Fig.8。

从Fig.7，Fig.8 可以看出，考虑对流换热边界会显著提高流道内对称点间的温度差，加剧了充填不平衡。如Fig.7(a)，在不考虑壁面滑移的情况下，当熔体温度为500 K 时，流道系统1 内，绝热壁面下对称点温差(ΔT)的最大值为0.312 K，ΔT的最小值为0.081 K。对流换热系数取2500 W/(m2·K)时，ΔT的最大值为33.35 K，ΔT的最小值为21.341 K。2 种情况下，考虑对流换热边界时的最大温差较绝热边界时高出33.038 K，最小温差高出21.26 K。流道系统2 内，绝热壁面下ΔT的最大值为0.122 K，ΔT的最小值为0.077 K。对流换热系数取2500 W/(m2·K)时，ΔT的最大值为32.64 K，ΔT的最小值为20.428 K。2种情况下，考虑对流换热边界时的最大温差较绝热边界时高出32.518 K，最小温差高出20.351 K。流道系统3 内，绝热壁面下ΔT的最大值为0.098 K，ΔT的最小值为0.062 K。对流换热系数取2500 W/(m2·K)时，ΔT的最大值为31.98 K，ΔT的最小值为19.037 K。2 种情况下，考虑对流换热边界时的最大温差较绝热边界时高出31.882 K，最小温差高出18.975 K。Fig.7(b)中，熔体温度为510 K 时，其变化规律与熔体温度500 K 时一致。Fig.8 中，在考虑壁面滑移的情况下，其变化规律与Fig.7 中不考虑壁面滑移一致。从以上数据可以得出，考虑对流换热会大幅度增加流道内对称点间温度差，严重加剧充填不平衡。

Fig.7 Influence of convective heat transfer boundary on temperature difference at symmetry point without wall slip

Fig.8 Influence of convective heat transfer boundary on temperature difference at symmetry point with wall slip

出现上述情况的原因是绝热边界条件下，流道内的热量来源是熔体与壁面间的剪切生热。而在考虑了对流换热情况下，一方面在高剪切速率下，熔体与壁面产生剪切摩擦热；另一方面微注塑过程中靠近壁面处的熔体与壁面有热交换，导致一部分热量的散失，使流道内靠近壁面处的熔体温度与流道中心处的熔体温度差异增大，流经分流道分岔口后，对称浇口间温度分布更不均匀。因此在同种条件下，考虑对流换热会加剧充填不平衡。

而对流换热系数值的不同，其影响充填不平衡程度也不相同。从Fig.7，Fig.8 分析，当h=1000 W/(m2·K)时与h=2500 W/(m2·K)时，对称点温度差异的不同。如Fig.8(a)，考虑壁面滑移的情况下，当熔体温度为500 K 时，流道系统1 内，h=2500 W/(m2·K)时，ΔT的最大值为11.543 K，ΔT的最小值为1.025 K；h=1000 W/(m2· K)时，ΔT的最大值为25.234 K，ΔT的最小值为5.146 K。2 种情况下，h=1000 W/(m2· K)时的最大温差较h=2500W/(m2· K)时高出13.691 K，最小温差高出4.121 K。流道系统2 内，h=2500W/(m2·K)时，ΔT的最大值为1.326 K，ΔT的最小值为0.783 K；h=1000W/(m2·K)时，ΔT的最大值为4.913 K，ΔT的最小值为0.742 K。2 种情况下，h=1000 W/(m2·K)时的最大温差较h=2500 W/(m2·K)时高出3.587 K，最小温差低出0.041 K。流道系统3内，h=2500W/(m2·K)时，ΔT的最大值为1.176 K，ΔT的最小值为0.537 K；h=1000 W/(m2· K)时，ΔT的最大值为3.656 K，ΔT的最小值为0.985 K。2 种情况下，h=1000 W/(m2·K)时的最大温差较h=2500W/(m2·K)时高出2.48 K，最小温差高出0.448 K。Fig.8(b)中，熔体温度为510 K 时，其变化规律与熔体温度500 K 时一致。Fig.7 中，在不考虑壁面滑移的情况下，其变化规律与Fig.8 中考虑壁面滑移一致。从以上数据可以得出，h的改变会影响对流换热程度，h越低，流道内对称点间的温度差反而升高，充填不平衡越明显。

相同的，在h=1000 W/(m2·K)，2500 W/(m2·K) 2种情况下，流道内的热量来源主要是摩擦剪切生热以及熔体与壁面间对流换热散失热量的差值。当剪切速率不变时，产生的摩擦剪切热是定量的。而当系数h减小时，根据垂直流动方向的法向热流密度公式(7)可知，法向热流密度减小，即熔体与壁面间对流换热散失的热量更少，导致流道内温度降低程度更小，熔体平均温度更高，因此对称点间温度差异更大，加剧了充填不平衡。

3.4 对流换热条件下流道尺度效应对充填不平衡的影响

与绝热边界不同，对流换热边界有热量损失，在此情况下微尺度效应对注塑过程的影响有所差异，因此为了探究对流换热条件下流道尺度效应对充填不平衡的影响，设置了3 种不同尺寸的流道进行对比分析，统计对称点温度差如Fig.7 和Fig.8。

从图中可以看出，微尺度效应对流道内温度差有着显著的影响。如Fig.7(b)，当不考虑壁面滑移及熔体温度为510 K 的情况时，绝热边界条件下，流道系统1，2，3 内的温差ΔT的最大值分别为0.498 K，0.374 K，0.202 K，ΔT的最小值分别为0.428 K，0.177 K，0.118 K；h=1000 W/(m2·K)边界条件下，流道系统1，2，3 内的温差ΔT的最大值分别为46.765 K，44.986 K，42.787 K，ΔT的最小值分别为30.562 K，28.946 K，28.512 K；h=2500 W/(m2· K)边界条件下，流道系统1，2，3 内的温差ΔT的最大值分别为34.314 K，33.245 K，32.165 K，ΔT的最小值分别为21.459 K，20.697 K，19.818 K。Fig.7(a)中，熔体温度为500 K 时，其变化规律与熔体温度510 K 时一致。Fig.8 中，在考虑壁面滑移的情况下，其变化规律与Fig.7 中不考虑壁面滑移一致。从以上数据可以得出，在考虑对流换热边界条件下，尺度效应会影响流道内对称点间的温度差异，且随着流道尺寸的减小对称点温差ΔT也在减小，充填不平衡得到改善。

这是因为当熔体的入口温度、剪切速率相同时，微流道的尺寸减小，导致其表体比相对增大，熔体与壁面间热传递的面积相对增加，即在壁面处的热量损失相对增多，而在剪切摩擦热定量的情况下，熔体平均温度随微流道半径尺寸的减小而逐渐降低，减小了对称点间温差，充填不平衡得到改善。