浅谈函数中任意性与存在性的问题分类

汕头市东厦中学(515000)李舜

函数的“任意性”与“存在性”问题,是高中数学常见的一个知识点,也是近几年高考的热点与考点.此类问题经常与函数导数、方程、不等式等相结合,考查学生分类讨论、数形结合、化归与转化等数学思想,综合性强,题型灵活多变.可有单函数、单变量问题;双函数、单变量问题;双函数、双变量问题等.对于这类问题,可利用函数导数的相关知识,借助图像理解,把不等关系或相等关系转化为函数的值域或最值问题来讨论.

对这类问题的研究,笔者整理了八种典型的类型,并结合实例进行辨析,供参考.

(一)若∀x ∈D,有a ＜f(x)恒成立⇔a ＜f(x)min;若∀x ∈D有a ＞f(x)恒成立⇔a ＞f(x)max.

这种类型属于单函数、单变量问题,在平时的解题中经常遇到,属于常见题型,一般可以用参变分离的方法来做.对f(x)进行求导,解得最值.

例1已知两函数f(x)= 7x2-28x - c,g(x)=2x3+ 4x2-40x,对任意x ∈[-3,3],都有f(x)≤g(x)成立,求实数c的取值范围.

分析本题对于形如∀x ∈D,f(x)≤g(x)的问题,有两种方法:第一,可以先构造函数h(x)=g(x)-f(x),再转化为∀x ∈D,h(x)≥0;第二,可以利用参变分离来做.

解析设h(x)=g(x)-f(x)=2x3-3x2-12x+c,问题转化为x ∈[-3,3]时,h(x)≥0 恒成立,故只需hmin(x)≥0.令h′(x)=6x2-6x-12=6(x+1)(x-2)=0,得x=-1或2.由导数知识,可知h(x)在[-3,-1]单调递增,在[-1,2]单调递减,在[2,3]单调递增,且h(-3)=c -45,h(x)极大值=h(-1)=c+ 7,h(x)极小值=h(2)=c -20,h(3)=c-9,所以hmin(x)=h(-3)=c-45,由c-45 ≥0,得c≥45.

(二)若∃x ∈D,有a ＜f(x)成立⇔a ＜f(x)max; 若∃x ∈D,有a ＞f(x)成立⇔a ＞f(x)min.

这种类型也属于单函数、单变量问题,与类型一具有可比性,也是常见题型,可以采用参变分离的方法,对f(x)进行求导,解得函数的最值.

例2已知两函数f(x)= 7x2-28x - c,g(x)=2x3+ 4x2-40x,存在x ∈[-3,3],使f(x)≤g(x)成立,求实数c的取值范围.

分析对于本题形如∃x ∈D,f(x)≤g(x)的研究,可以构造函数h(x)=g(x)-f(x),再等价为∃x ∈D,h(x)≥0.

解析据题意,存在x ∈[-3,3],使f(x)≤g(x)成立,即为:h(x)=g(x)-f(x)≥0.在x ∈[-3,3]有解,故只需hmax(x)≥0,由例1 知hmax(x)=c+7 ≥0,于是得c≥-7.

(三)若∀x1∈A,∀x2∈B,都有f(x1)≤g(x2)⇔

fmax(x)≤gmin(x).

这种类型是双变量、双函数问题,学生一开始接触的时候会比较茫然,此时可以画出函数图像进行引导,利用数形结合的思想,得出解题思路.

例3已知两函数f(x)= 7x2-28x - c,g(x)=2x3+ 4x2-40x,对∀x1∈[-3,3],∀x2∈[1,4],都有f(x1)≤g(x2),求实数c的取值范围.

分析它与例1 虽然都是不等式恒成立问题,但却有很大的区别,对∀x1∈[-3,3],x2∈[1,4],都有f(x1)≤g(x2)成立,不等式的左右两端函数的自变量不同,x1,x2的取值在各自定义域上具有任意性,因此要使不等式恒成立的充要条件是:fmax(x)≤gmin(x).

解析因为

f(x)=7(x-2)2-c-28,x ∈[-3,3],

所以f(x)∈[-c-28,-c+147],因为

g′(x)=6x2+8x-40=2(3x+10)(x-2),x ∈[1,4],

所以g(x)∈[-48,32],因为fmax(x)≤gmin(x),所以147-c≤-48,即c≥195.

(四)若∃x1∈A,∃x2∈B,使得f(x1)≤g(x2)⇔fmin(x)≤gmax(x).

有了以上三种类型的分析与探讨,则第四种类型也变得容易理解.同样地可以利用函数图像进行分析,对图像位置进行平移,得出临界条件.

例4已知两函数f(x)= 7x2-28x-c,g(x)= 2x3+4x2-40x,∃x1∈[-3,3],∃x2∈[1,4],使得f(x1)≤g(x2),求实数c的取值范围.

分析∃x1∈[-3,3],∃x2∈[1,4],使得f(x1)≤g(x2),只需f(x)的最小值不大于g(x)的最大值.

解析由例3 得,在定义域内,fmin(x)=-c -28,gmax(x)=32,因此只需fmin(x)≤gmax(x),即-c-28 ≤32,所以c≥-60.

(五)若∀x1∈A,∃x2∈B,使得f(x1)≤g(x2)⇔fmax(x)≤gmax(x).

例5已知两函数f(x)= 7x2-28x-c,g(x)= 2x3+4x2-40x,∀x1∈[-3,3],∃x2∈[1,4],使得f(x1)≤g(x2),求实数c的取值范围.

解析由例3 得,在定义域内,fmax(x)=-c+ 147,gmax(x)= 32,因此只需fmax(x)≤gmax(x),即-c+147 ≤32,所以c≥115.

(六)若∃x1∈A,∀x2∈B,使得f(x1)≤g(x2)⇔fmin(x)≤gmin(x).

例6已知两函数f(x)= 7x2-28x - c,g(x)=2x3+ 4x2-40x,∃x1∈[-3,3],对∀x2∈[1,4],使得f(x1)≤g(x2),求实数c的取值范围.

解析由例3 得,在定义域内,fmin(x)=-c -28,gmin(x)=-48,因此只需fmin(x)≤gmin(x),即-c-28 ≤-48,所以c≥20.

(七)若∃x1∈A,∃x2∈B,使得f(x1)=g(x2)⇔f(x)的值域与g(x)的值域交集非空.

解析由例3 得,在定义域内,f(x)∈[-c-28,-c+147],g(x)∈[-48,32],因此只需f(x)的值域与g(x)的值域交集非空.我们可以利用补集的思想,先算两值域交集为空集时的情况,再求其补集即可.即-c+ 147＜-48 或-c-28＞32,解得c ＜-60 或c ＞195,所以本题答案为-60 ≤c≤195.

(八)若∀x1∈A,∃x2∈B,使得f(x1)=g(x2)⇔f(x)的值域是g(x)的值域的子集.

例8已知两函数f(x)= 7x2-28x - c,g(x)=2x3+ 4x2-40x,若对于∀x1∈[-3,3],总∃x2∈[1,4],使得f(x1)=g(x2)成立,求实数c的取值范围.

解析由例3 得,在定义域内,f(x)∈[-c-28,-c+147],g(x)∈[-48,32],因此只需f(x)的值域是g(x)的值域的子集.因此只需满足

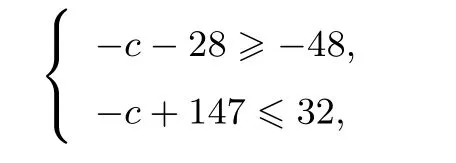
解得c ∈∅.

由上述例题可以看出,此类型题含有两个函数,两个变量,且两个变量没有关联,在各自的区间内取值具有任意性.任意性与存在性的综合问题成题形式多变,如果一味拘泥于结论,则会让思维僵化.解题时应灵活运用数形结合的思想,转化为函数最值或值域问题加以解决.其中,求函数最值或值域的方法多样,可涉及函数导数、分离常数、分类讨论、数形结合等多种手段与思想,对学生的能力是一种极好的考察.特别声明,本文所阐述的类型结论都是在默认最值存在的前提之下,当给定区间为非闭区间或函数非连续时,其最值可能无法去到,此时须确定其上或下确界,并考虑等号能否取得.