课程思政融入统计学教学的探索
2022-06-15吴爱娟贾鲁军
吴爱娟 贾鲁军
(1.北京工商大学嘉华学院 北京 101118;2.中国人民大学 北京 100872)
0 引言
在全面推进高校课程思政建设的背景下,通过《统计学》的教学,寓价值观引导于知识传授和能力培养之中,使得知识学习与思政教育同向同行,培养出具有正确世界观、人生观、价值观、创新能力及爱国的大学生。
1 大学思政教育的必要性和意义
当今时代是高速发展的信息化社会,大学生的思想活跃,容易接受一些新思想,为了大学生身心的健康成长,对其进行思政教育是很必要的。作为一名大学教师,笔者深知思政教育的重要性,一直在思考如何把思政教育糅合到所讲授的《统计学》课程里,挖掘《统计学》中的思政元素、撰写思政教学案例,教学效果良好,总结出来以抛砖引玉。
2 《统计学》课程思政建设探索
在当今信息化、大数据时代,统计学的学习显得尤为重要。《统计学》的学科特点是与数据有关,基于统计学的这一学科特点,我们深入挖掘思政元素,对思政建设进行了探索。
2.1 激励学生大量的阅读,拓宽知识面
2.1.1 寻找与强国差距,鞭策自我
《统计学》开篇给学生们介绍无处不在的统计学时,我们列举很多生活中、社会经济中的例子,比如各国科技研发投入额,我国各年科技研发投入额,感叹科技发展速度迅猛的同时也要意识到我国和强国之间的差距,借此教育引导学生珍惜学习时光,心无旁骛求知问学,增长见识,丰富学识,以建设、报效祖国。
2.1.2 学习统计学家们的创新思维
在推断统计中讲解假设检验时,为引入假设检验的思想和概念,用“女士品茶”引例,介绍“女士品茶”的故事背景,要鼓励我们的学生要像统计学家费歇尔那样,时刻抱有勇于创新的精神,沿着求真理、悟道理、明事理的方向前进。
2.1.3 阅读的力量
在讲解《统计学》第一章统计学概述时,抛给大家问题:毛泽东一生究竟读了多少书?
读过哪些书?该问题的解决需要搜集数据、整理数据,引入学习统计学的必要性的同时让同学生感受到了伟人的阅读史、体会到阅读的力量及博览群书的重要性。
《统计学》学业评价中有一项是读书笔记或者读书心得,鼓励大家去阅读各种统计读物、统计学发展史和统计学家的传记,以增长见识。
2.2 提高学生的思想道德修养
在讲解《统计学》中的抽样调查及数据整理时,给同学们布置实践作业:首先分组,5~8位同学一组,根据自己感兴趣的生活现象,撰写一份调查问卷。鼓励同学们撰写有关家风家规、中国文化等方面的调查问卷。
通过该作业,让学生了解到有家风家规家庭的比重、家风家规的重要性。同时让学生了解到中国文化的根本精神、中国文化的博大精深、中西文化的差异、中西文化各自的优劣等。
2.3 培养热爱祖国、奉献祖国的大学生,对中国特色社会主义道路及制度充满自信
2.3.1 数据展示中国的理论、制度的优越性
在讲解《统计学》中的时间序列时,抛给大家任务:请搜集中华人民共和国作为强国的数据及能够体现中国飞速发展的数据。比如同学们搜集历年GDP、人均GDP、全国邮电业务总量、中国共产党党员人数、汽车总量、大学生毕业人数等。通过这一任务的完成,既让大家知道了时间序列的定义、发展水平、发展速度及增长速度的概念和计算等知识点,又让学生切身体会到中国的强大,对中国特色社会主义道路及制度充满自信。
在这一任务的完成中,可能有的同学会搜集北京市历年雾霾日数,从数据中我们可以看到雾霾天数是历年减少的,相信我们政府在党的正确领导下一定能治理好我们的生存环境。当然,我们也要意识到治理环境的道路是艰难的,不能急于求成。各大经济强国都经历过雾霾困扰,英国用了近30年来治理它。
2.3.2 借助推断统计增强中国特色社会主义道路的自信
在推断统计中讲解假设检验时,可以搜集各大强国失业率和我国失业率,进而检验各国之间失业率有无显著性差异;可以搜集近两年雾霾天比例在政府治理后有无显著性提高等,用数据说话,借助推断统计,增强中国特色社会主义道路自信、理论自信和制度自信。
3 《统计学》课程思政案例撰写举例
举例一:加强道路自信、制度自信——两个总体比率差的假设检验。
(1)背景:新中国成立以来,党和国家各项事业取得辉煌成就,中国人民实现了从站起来、富起来到强起来的伟大历史性飞跃。取得这些伟大历史性成就的重要原因,就在于我们党带领全国各族人民探索形成了一条根植于中国大地、反映中国人民意愿、适应时代发展要求的中国特色社会主义道路。
讲解假设检验时,通过身边有趣的例子来阐述假设检验的思想和方法,大大激发学生的学习热情,同时增强中国特色社会主义道路自信和文化自信,对其进行思政教育是很必要的。
(2)目的:理解假设检验的思想;会对两个总体比例差做假设检验;通过实际举例,增强学生对中国特色社会主义道路自信、理论自信、制度自信和文化自信。
(3)实施:首先,利用几分钟时间让学生讨论一下体现一个国家制度优越性的指标有哪些?其次,回顾:小概率原理。最后,通过引例,从有趣性和常见性两个角度提出两个实际问题,通过启发式教学解决这两个问题,进而引入假设检验的思想和有关的基本概念的教学。
举例二:阅读中国著名的概率统计学家传。
(1)背景:《商务统计》课程中的知识点历来是学生学习的难点,学习兴趣下降,原来的考核方式:考勤分+作业分+期末闭卷考试分,导致不及格率很高。促使老师们进行课程改革,其中包含考核评价改革。考核评价朝着更多元、更全面进行改革。其中一项考核方式就是通过小组搜集有关的数学史、名家资料,写出感悟或者答辩,进而获得一定的平时表现成绩。
目前,随着我国经济的快速发展,部分学生的家庭经济条件优渥,没有生活压力,从小过着饭来张口、衣来伸手的生活,缺乏吃苦耐劳、奉献精神等。
(2)目的:实现学生考核评价多元化、全面化,通过小组搜集名家资料,写出感悟或者答辩进而获得平时表现成绩;通过阅读数学史、数学家的资料,感受到数学的有趣性、有用性,激发学生的学习兴趣;厚植爱国主义情怀,提醒学子们在进行科学研究时要以国家为担当,追求自己的理想与人生价值。
(3)实施:第一步,给学生布置阅读任务。开学初,对《商务统计》课程的两个班分成15个小组(每个小组人数为5~10位),各小组搜集我国概率统计方面的名家资料,写出感悟。期中时班级交流感悟,来完成任务获得相应的成绩。第二步,期中验收。他们搜集的概率统计学家有许宝騄、陈希儒、陆传荣、戴世光等,全方位地了解了他们生平,包括各自的学术研究成果。下面以中国概率统计学家的先驱许宝騄先生为例(见表1)。

表1
(4)总结:通过阅读名家资料,激发了学生的学习兴趣;通过小组合作完成任务,既提高了成绩又增强了团队合作意识、培养了阅读和查阅资料的能力、训练了写作和演讲能力;数学家们鞠躬尽瘁、死而后生的精神感动着我们,他们严谨的治学精神、一丝不苟的工作态度、吃苦耐劳的精神激励着我们;学生意识到“科学无国界,但是科学家有国界”,厚植了爱国主义情怀。
举例三:二项分布的应用——大学生要讲诚信、要具有真才实学。
(1)背景:大学生是国家未来的建设者和接班人。大学生要在增长知识见识上下功夫,教师教育引导学生珍惜学习时光,心无旁骛求知问学,增长见识,丰富学识,沿着求真理、悟道理、明事理的方向前进等。目前,校园中作弊、平时混日子靠运气考试及格的现象屡见不鲜了,因此有人断言“当今大学生成绩水分高、不具备真才实学、诚信出了问题等”,基于此,我们做这一教学案例,借此教育学生要守诚信、要具备真才实学的同时也体会到概率统计的有用性和有趣性。《商务统计》课程中的二项分布是生活中很多随机现象遵循的,若能让学生学会用它们解决实际问题,体会到它们的有用性,更能激发他们学习这部分内容的积极性。
(2)目的:掌握二项分布;能够把二项分布应用于实践,分析解决实际问题;用概率统计知识教会大家要讲诚信、要具备真才实学,体会到概率统计的魅力及有用性;理解“小概率原理”。
(3)实施:首先介绍二项分布产生的背景:贝努利试验及n重贝努利试验。其次用引例:连续抛掷一枚均匀骰子,求4次抛掷中6点恰好出现3次的概率,引入二项分布的定义,最后用二项分布来解决实际问题:例1碰运气能过英语四级吗?例2根据某高校教务处的调查,表明有四分之一的同学在考试中会作弊,考虑一个有20个学生的班级。若你在一次课程考试的监考中发现恰有12人作弊,此时你是否怀疑该教务处调查结果的准确性?
(4)分析讨论:二项分布产生的背景是什么?二项分布B(n,p)中的参数n和p分别指什么?实际问题中如何建模出二项分布来?
二项分布产生的背景是贝努利试验,即结果只有A和,且每次试验中A发生的概率P(A)=p。在n重贝努利试验下记A发生的次数为X,则
例1碰运气能过英语四级吗?
假设英语试卷100分,60分及格。除了15分作文和15分翻译外,其余70道题均为选择题,每道题有4个可供选择的答案,每题1分。问:单靠运气能通过英语四级考试吗?
假设不考虑写作和翻译所占的30分,且每道选择题都是单选题,即只有一个正确答案。做了70个选择题相当于做了70次贝努利试验,把作对记作A,则。

则靠运气通过英语四级考试的概率是
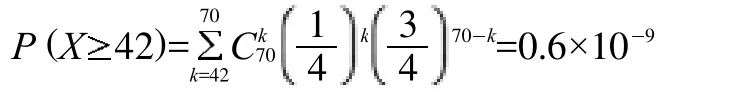
一亿个想碰运气的考生中,仅有大约0.6个能通过英语四级考试!因此我们学生要珍惜学习时光,心无旁骛求知问学,增长见识,丰富学识,不要想着走捷径,靠运气。
例2根据某高校教务处的调查,表明有四分之一的同学在考试中会作弊,考虑一个有20个学生的班级。若你在一次课程考试的监考中发现恰有12人作弊,此时你是否怀疑该教务处调查结果的准确性?
观察20个学生考试相当于做了20次贝努利试验,把“作弊”记作A,则。
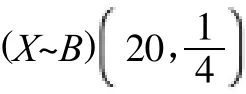
则12人作弊的概率是
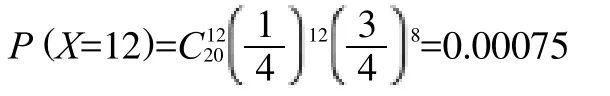
该概率不足千分之一,是一个小概率。在一次观察中,小概率事件发生了这是不正常的,所以我们有理由怀疑教务处调查结果的准确性。
由例2,我们引入了“小概率原理”:在一次试验中,小概率事件几乎不发生。为以后假设检验的学习提供了基础。
(5)结论:通过这些例子,学生掌握了二项分布,能够把二项分布应用于实践,分析解决实际问题。同时用概率统计知识教会大家要讲诚信、要具备真才实学,要在增长知识见识上下功夫,教育引导学生珍惜学习时光,心无旁骛求知问学,增长见识,丰富学识,沿着求真理、悟道理、明事理的方向前进等。
