蜻蜓非均匀柔性前翼扑动飞行的气动性能研究1)
2022-06-13刘笑尘何心怡何国毅孙书美
刘笑尘 何心怡 何国毅 王 琦 孙书美
(南昌航空大学飞行器工程学院,南昌 330063)
引言
扑翼飞行器相比于固定翼飞行器具有隐蔽性、机动性和灵活性等特征,满足现在现代化战争的需求,可以更好的运用于军事侦查和精确打击[1].在以美国为引领的多个国家[2],扑翼飞行器的研究在近来二十几年当中掀起了一股浪潮[3].虽然有关于扑翼的研究文献越来越多,但是大部分的工作集中于刚性扑翼在非定常条件下气动规律的研究,在真实情况下,扑翼无论其尺寸大小都具有一定的柔性因此柔性翼结构变形引起的流场和气动参数变化的研究具有重要意义.
在自然界中,一些动物通过翅膀、鳍、尾部、躯干等结构的摆动来获得推力以及升力是非常普遍的现象.Liu等[4]发现适当的组合柔性扑翼频率和弯曲度可以显著改变推力的产生和压力分布,提供更高的气动效率.Chen等[5]在得出改进后的UAM 非定常气动模型后,计算得出柔性翼相比于刚性翼来说减小了负升力.文献[6]在流体和结构相互作用领域的发现表明,柔性机翼可以比刚性机翼产生更多的升力.Addo-Akoto等[7]通过对比柔性翼与刚性翼气动参数,结果表明柔性翼产生的力表现出了明显的相位延迟.以上均为对于扑翼固定柔性的研究,但是柔性对于扑翼气动参数的影响,还包括展向柔性[8-11]和弦向柔性两个重要的领域[12-13].张云飞等[14]对于展向柔性的研究表明沿展向引入柔性改变了扑翼有效攻角,适当的展向柔性可以减小阻力,过大的展向柔性增加阻力.文献[15]研究了在低雷诺数条件下,扑翼的展向柔性和弦柔性对扑翼性能的影响,引入一定的展向柔性可以增加推进效率.被动的柔性变形在很多的实验中被证明是可以增加运动效率[16-19].值得一提的是,飞行类动物的翅膀柔性不是均匀分布,而且这种不均匀分布反而提高了推进效率[20].Wood[21]发现当水翼的前1/3 部分的柔性比较小,后2/3 部分的柔性比较大时,推进效率是最高的,也就是不均匀的柔性分布的推进效率要优于均匀柔性分布.
随着扑翼发展,当需要尺寸在15 cm 以下的飞行器进行作战任务时,微小型扑翼飞行器(flapping micro aerial vehicle,FMAV)就起到了至关重要的作用.卓越的飞行本领使得蜻蜓成为了研究微小型扑翼飞行器最适合的仿生对象.Hamamoto等[22-23]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,表明柔性翅膀的变形对气动特性具有较小的影响.郑光鹏[24]对于蜻蜓翅二维截面进行流固耦合计算,得出翼型越薄变形越大,扑动频率越大产生的推力和升力越大,适合于大前飞速度.徐明等[25]通过主动控制二维蜻蜓翼截面的变形,计算了二等蜻蜓翼型截面周期性的动态柔性变形引起的气动力响应,发现在下拍过程中,动态柔性变形显著提高升力和推力.郝淑文[26]利用Matlab 编程建立了适合求解柔性翼气动效能的程序,发现扑动平面与水平面的夹角在一定范围内增大,可以提高推力和升力系数.孟令兵等[27]基于计算流体力学/计算结构力学(CFD/CSD)的双向流固耦合方法,通过C++编程计算了前缘具有较大刚性的蜻蜓后翼平板模型在同一前飞速度下的气动参数,发现了柔性翼降低了飞行阻力提高推力.蜻蜓翼飞行性能的研究大多数集中在均匀柔性分布下的二维柔性截面对于气动性能影响的论述,但是蜻蜓的飞行是一个三维问题.本文就弦向柔性对于蜻蜓前翼气动性能的影响展开研究.在前人对于扑翼流固耦合研究的基础上,根据三维蜻蜓翼模型来探究均匀柔性分布和变柔性情况下对于蜻蜓前翼气动性能参数的影响,对比柔性翼在两种柔性分布方式下相对于刚性翼的优劣势.
1 扑翼模型与函数
1.1 几何模型建立
通常蜻蜓的两侧翼距离较大,相互干扰的作用较小,文献[28]研究了蜻蜓悬停时的身体同侧的前后翼并没有很大的相互干扰作用,故本文选取了一个蜻蜓右前翼,模拟单独的蜻蜓翼挥拍过程中的柔性变形,忽略蜻蜓翼之间的相互干扰.
蜻蜓前翼具有非常复杂的微观结构,由于文献[29]通过数值模拟方法,表明凹凸不平的褶皱结构并不影响扑翼整体的气动响应,故而本次计算过程中将蜻蜓前翼简化成具有相同轮廓的柔性平板模型,根据蜻蜓前翼的尺寸参数[30],建立蜻蜓前翼的几何模型如下图1 所示,几何参数包括:平均弦长C为8 mm,展长L为40 mm,厚度 σ 为0.18 mm 以及几何面积S为284.1 mm2.

图1 蜻蜓前翼平板模型Fig.1 Plat model of dragonfly forewing
1.2 扑动函数
确定扑动函数需要确定两个因素:扑动幅值和扑动频率.扑动幅值以及扑动频率依照蜻蜓的飞行特点进行确定,在实际飞行过程中,蜻蜓扑动幅值在10°~ 60°以及扑动频率在30 Hz~ 50 Hz[31].在具体设置蜻蜓前翼的扑动函数时,根据文献采用20°扑动幅值和43 Hz 扑动频率[30].给出扑动示意图如图2以及扑动函数为
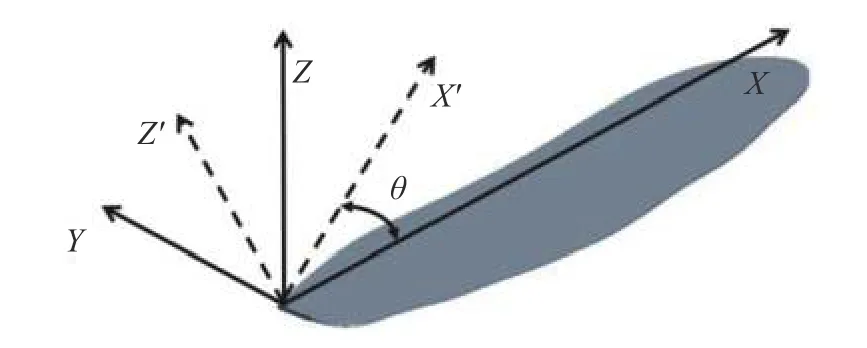
图2 前翼扑动示意图Fig.2 Schematic diagram of front wing flutter

根据扑动角度函数先转化为弧度制再进行求导,得到其扑动角速度函数

1.3 柔性分布函数
蜻蜓前翼从前缘到后缘的柔性分布模式有两种.(1)连续均匀分布:蜻蜓前翅的柔性从前缘端到后缘端都是相同的;(2)连续变化分布:本文将蜻蜓前翼的柔性从前缘端到后缘端按函数规律变化,包括线性函数,平方函数.
在变柔性分布中定义蜻蜓前翼前缘杨氏模量17 GPa[27],定义后缘杨氏模量3.8 GPa[30].通过Position 场函数,调用前翼随体坐标系中y坐标.因此前后缘的y坐标和杨氏模量构成两对坐标点,得出(0.002,17)和(-0.006,3.8).线性函数表达式通过两点即可得到,将二次函数顶点置于前缘处,并求解通过两点的函数,即可得到平方函数的表达式.整个蜻蜓前翼根据柔性分布函数发生柔性变化:
均匀柔性分布
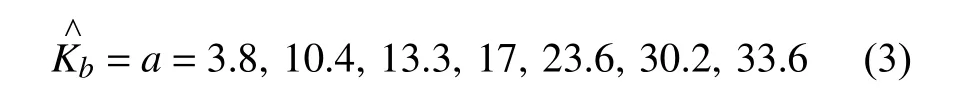
线性函数柔性分布
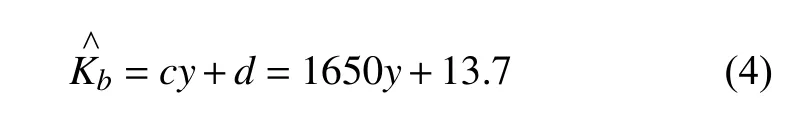
平方函数柔性分布
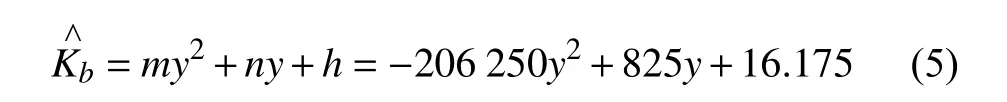
2 研究方法
2.1 计算方法
采用STAR-CCM+计算流体力学软件,对蜻蜓前翼扑动模型进行双向流固耦合分析.
刚性翼的扑动研究较较为简单,主要采用动网格技术[30]实现对蜻蜓前翼扑动的仿真计算.柔性翼由于变形较大导致网格剧烈变化,因此在流固耦合的基础上采用重叠网格和网格自适应技术.
将外流场和重叠区域均设置为流场域,流场域选择隐式非稳态求解,湍流模型选择Spalar-Allmaras湍流模型[32].在流场域中,设置重叠保护和单元网格质量校正,来提高扑动过程中的流域网格质量,重叠区域设置为浮动,可以跟随前翼固体模型一起运动.
将前翼结构设置为固体区域,在固体域中采用隐式非定常固体应力求解模型,添加扑动函数和杨氏模量函数使蜻蜓前翼实现运动及柔性分布.
将固体区域中的前翼表面和重叠区域中的前翼表面设置为映射接触面,用于数据传递.在求解器中添加流体结构耦合(双向),再在固体运动的基础上添加固体变形位移即可实现在扑动过程中叠加变形,变形后的结构重新计算气动力,数据在此界面上一直相互传递,由此来实现双向流固耦合.
2.2 控制方程
流体控制方程包含连续性方程和运动方程,其中连续性方程如下
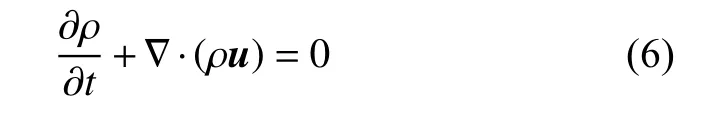
运动方程
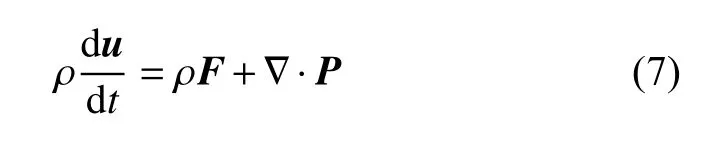
式中,ρ 为密度;u代表流体微团的速度矢量;F表示作用在单位质量上的质量力;P为应力张量.
固体控制方程一般由牛顿第二定律导出,如下

式中,ρ 是固体密度;σ 是柯西应力张量;F是体积力矢量;d是固体域当地加速度矢量;流固耦合需要流体域和固体域之间交换数据,该过程必须满足一些物理量的相等和守恒,即满足方程如下
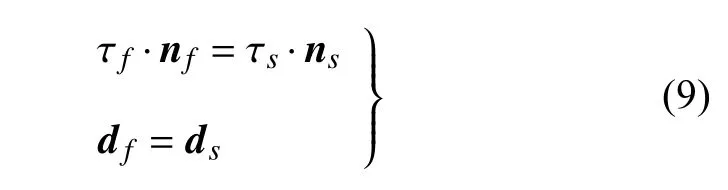
式中,τs和 τf分别代表固体域与流体域力大小;ns和nf则接触表面的法向单位向量;ds和df代表固体域与流体域微团位移矢量;第一项表示交界面上的流体域与固体域力相等,第二项表示位移相等.
3 计算前处理
3.1 流场区域网格划分
建立一个长方体外流域,其尺寸大小为30C×30C×25C,如图3(a)所示.将靠近蜻蜓前翼翼根的面的边界条件设置为对称面,将左面和上下面设置为速度入口边界条件,上下边界使用速度入口条件可以减少边界对流场的影响[33],右面的边界条件设置为压力出口.
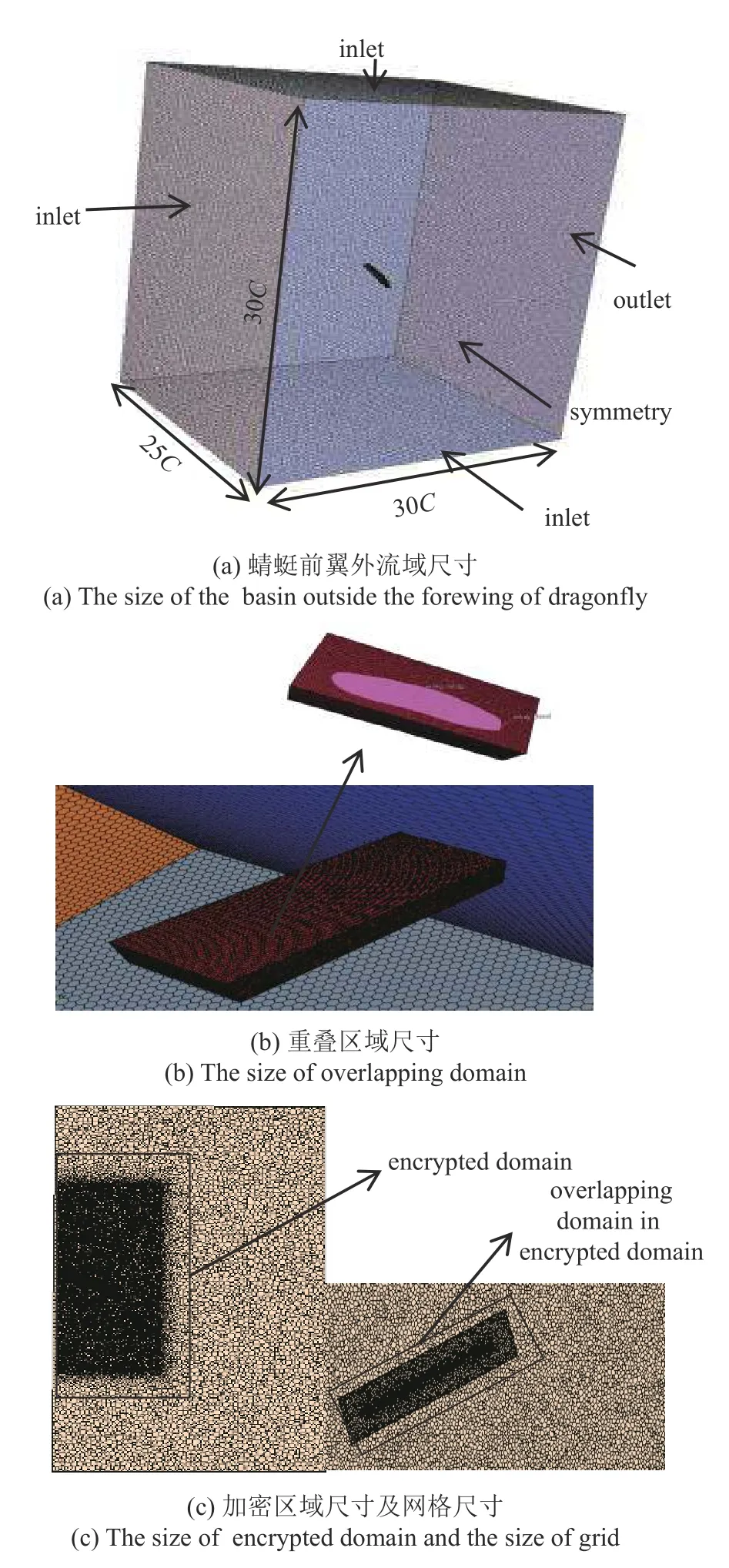
图3 流体区域尺寸及网格Fig.3 The size of fluid domain and mesh
流域网格划分采用多面体网格生成器和网格重构方法来提高网格质量.在流体域中增加体控制设置为加密区域,使得蜻蜓前翅在扑动过程中始终处于加密区域,采用多面体网格方法合理设置加密区域的尺寸大小和网格尺寸,保证了扑动时计算的精确性.
重叠区域采用多面体网格和网格重构方法划分网格,区域大小如图3(b)所示,翅翼的边界层网格采用4 层棱柱层网格.加密区域尺寸及重叠区域在加密区域中的相对网格尺寸如图3(c)所示.
3.2 固体域网格划分
CSD 的数值方法之一是有限元法,将三维蜻蜓前翼的翼根为固定面,翼面为交界面,采用四面体网格和薄体网格的方法离散化蜻蜓前翼,即可得到固体求解时的有限元网格,固体域网格如图4 所示.

图4 蜻蜓前翼平板模型网格Fig.4 Mesh of forewing plat model
3.3 数值方法验证
为了验证本文方法的数值计算扑翼运动的正确性,选取了文献[34]扑翼运动模型,并将计算结果同文献结果对比.对比结果如图5 所示,升力系数曲线随时间的变化的趋势极为近似,数值大小较为接近,因此该方法可以用于数值分析扑翼运动的气动特性.

图5 升力系数随时间变化规律与文献[34]对比结果Fig.5 The variation law of lift coefficient with time is compared to the results in Ref.[34]
3.4 网格无关性验证
本文在来流速度为3 m/s、扑动频率为43 Hz、扑动幅值为20°情况下,采用三套网格对蜻蜓前翼升力系数进行监测如图6 所示,Case A 网格数为160 万,Case B 网格数为230 万,Case C 网格数为280 万.可以看出来升力系数曲线图基本一致,考虑到计算效率以及计算结果准确性,本文选用230 万网格数进行计算.
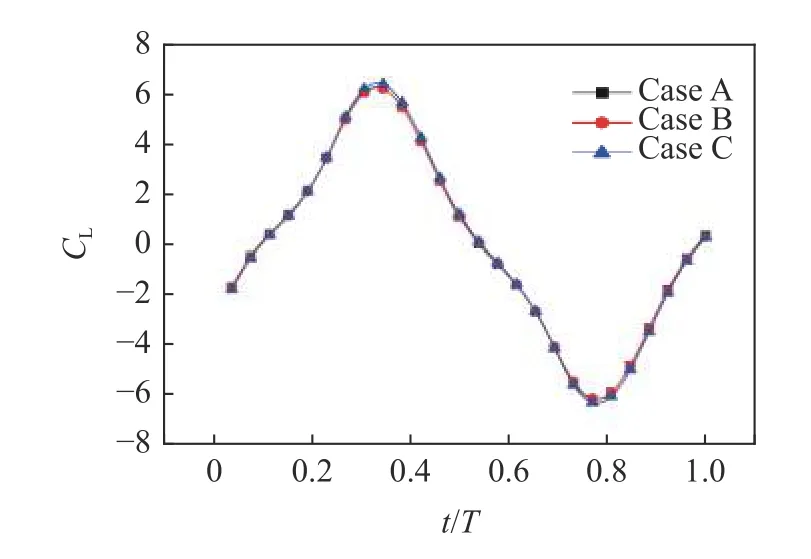
图6 网格无关性验证Fig.6 Verification of independence of grid number
4 不同柔性分布下柔性翼结构变形结果与分析
4.1 不同柔性分布下柔性翼扑动过程
在均匀柔性分布条件下,蜻蜓前翼虽然都是在上扑结束和下扑结束时刻到达变形最大值,但是杨氏模量的变化导致前翼出现了不一样的变形规律.例如在扑动过程中:(1)当杨氏模量较小时,如图7(a)所示,翼尖在0T时刻达到最大下弯变形,在T/2时刻达到最大上翘变形,0T时刻虽然翼根部位处于最大上扑动角度状态,但是翅翼整体处于最大下弯变形状态;(2)当杨氏模量较大时,如图7(b)所示,翼尖在0T时刻达到最大上翘变形且在T/2 时刻达到最大下弯变形,0T时刻翼根处于最大上扑动角度状态,翅翼整体处于最大上翘变形状态.
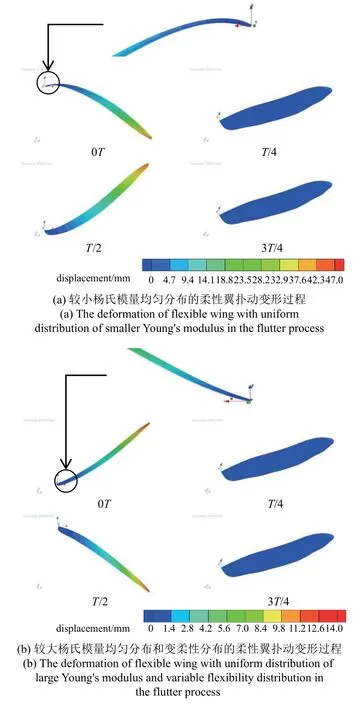
图7 柔性翼扑动变形过程Fig.7 The deformation of flexible wing during flapping
在变柔性分布条件下,在扑动过程中蜻蜓前翼变形规律与杨氏模量较大时的翅翼变形规律保持一致,如图7(b)所示.
4.2 不同柔性分布下柔性翼结构变形数值监测方法
采取在监测点监测变形量的方法,更容易准确得出柔性翅的翼尖变形量和扭转变形量即扭转角度.在翼尖处放置一个监测点F,用来监测翼尖在z 轴的变形量.分别在距离翼根20 mm (翼中部位)和36 mm 处(翼尖部位)的前,后缘放置4 个监测点分别命名为A,B,C,D监测前后缘在z轴的变形量,监测点位置如图8 所示.

图8 蜻蜓前翼的监测点位置Fig.8 Location of monitoring points on the forewing
4.3 不同柔性分布下柔性翼数值变形结果及流场分析
翼尖点F 的监测变形量随时间的变化如图9 所示,可以发现:(1)均匀柔性较大的前翼翼尖变形和均匀柔性较小、变柔性分布的翼尖变形的规律相反,和前文的扑动变形过程相对应;(2)变柔性分布时,二次函数分布时翼尖点最大变形量较小,这是因为二次函数柔性分布时在靠近前缘部位,杨氏模量的减小速度较慢,因此到达翼尖位置时杨氏模量大于一次函数柔性分布.
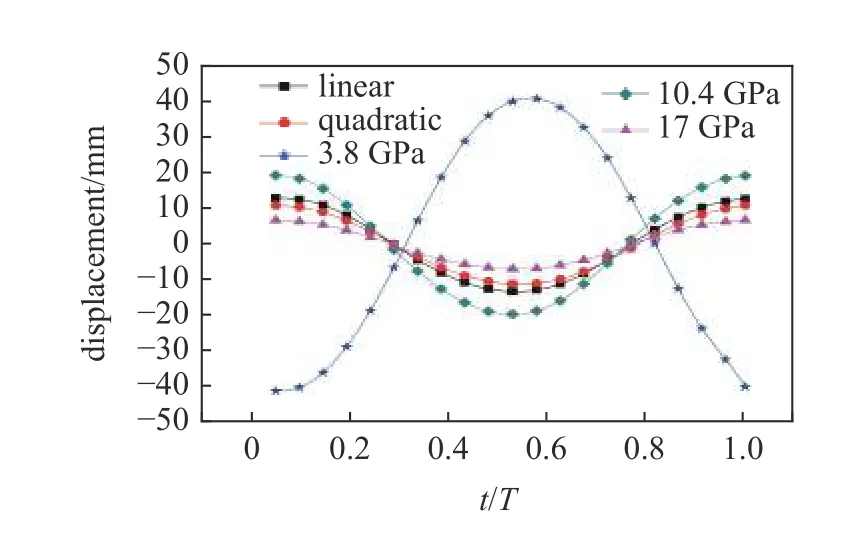
图9 不同柔性分布下柔性翼的翼尖变形Fig.9 Tip deformation of flexible wing with different flexibility distributions
选取杨氏模量为3.8 GPa 均匀柔性分布和杨氏模量为10.4 GPa 均匀柔性分布的柔性翼在一个周期的初始时刻翼尖部位的压力云图,如图10 和图11所示.

图10 杨氏模量为3.8 GPa 均匀柔性分布压力云图Fig.10 Pressure contours of uniform flexible distribution with Young's modulus of 3.8 GPa
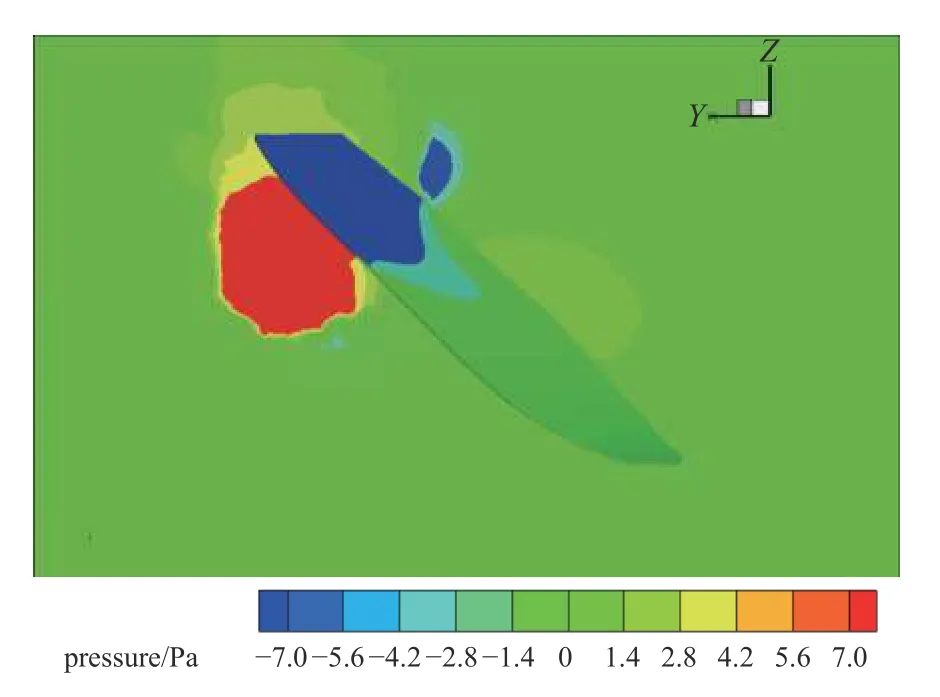
图11 杨氏模量为10.4 GPa 均匀柔性分布压力云图Fig.11 Pressure contours of uniform flexible distribution with Young's modulus of 10.4 GPa
从杨氏模量为3.8 GPa 均匀柔性分布的压力云图可以看出,上翼面压强大于下翼面压强是导致翼尖变形量在初始时刻为负位移的原因.
从杨氏模量为10.4 GPa 均匀柔性分布的压力云图可以看出,上翼面压强小于下翼面压强从而导致翼尖变形量在初始时刻为正位移变形.
可见柔性过大会导致翼尖会发生相反的柔性变形规律.
根据监测点A,B,C,D位移可以得到后缘减前缘即(B-A和D-C)的差值,示意图如图12 所示.当差值为正时,表示后缘点在前缘点上方,此时扭转角度为负,当差值为负时,表示后缘点在前缘点下方,此时扭转角度为正.

图12 后缘点与前缘点差值示意图Fig.12 Schematic diagram of difference between trailing edge point and leading edge point
再根据监测点之间的差值代入扭转角公式可以得出蜻蜓前翼在翅翼中部和翼尖部位的扭转角度.整个翅翼伴随着扑动过程也一直在按照余弦函数规律做扭转振荡运动,差值最大值时刻对应的也就是扭转角度曲线最大幅值时刻.
翅翼扭转角度曲线的周期和扑动周期一致,因此确定幅值后也就得到了扭转曲线,初始时刻的最大幅值如下表1 所示.其中β1代表的是在翼中部位20 mm 处的扭转角,β2代表的是在翼尖部位36 mm处的扭转角.扭转角为正则此刻迎角为正,扭转角为负则此刻迎角为负.

表1 蜻蜓前翼0T 时刻的扭转角幅值Table 1 Torsional angle amplitude of dragonfly forewing at 0T
在均匀柔性分布时:(1)扭转振荡幅值随着杨氏模量的增加逐渐减小,杨氏模量较小时在初始时刻的扭转角度为正,与其他柔性分布相反,也是因为扑动过程的变形规律相反造成;(2)翼中和翼尖部位扭转振荡幅度不同,随着杨氏模量的增加,又基本保持一致.
在变柔性分布时,翼尖部位的扭转幅度大于翼中部位,说明翼尖部位后缘的上翘和下弯变形略微大于翼中部位的后缘.
5 不同柔性分布下蜻蜓前翼气动特性分析
5.1 不同柔性分布下蜻蜓前翼的升力系数
从升力系数变化规律如图13 所示,对比可以发现:(1)在均匀柔性分布时,柔性较大的翅翼升力系数曲线变化趋势滞后于刚性翼半周期,这是因为从结构变形来看,将下扑运动离散之后,每个瞬时时刻刚性翼相对于来流做向下扑动运动,柔性较大的前翼相对于来流来说做向上变形运动,从而导致了半个周期的刚性翼向下运动,变为了向上变形运动;(2) 在变柔性分布时,柔性翼和刚性翼的变化趋势相同.
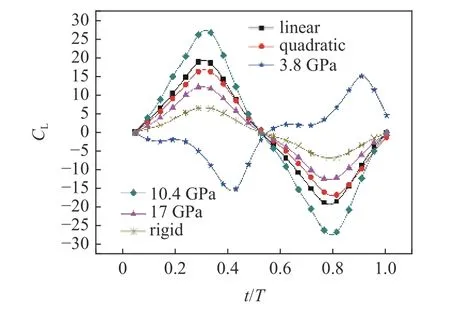
图13 不同柔性分布下柔性翼的升力系数Fig.13 Lift coefficients of flexible wings with different flexibility distributions
两种柔性分布情况下,因为运动为单自由度的扑动运动,扑动过程上下对称,所以只提高了升力系数峰值,并未改变正升力系数在一个周期内的时间占比,并没有提高平均升力系数.
为了探究柔性翼如何提高升力系数峰值,本文选取线性函数柔性分布的柔性翼和刚性翼下扑过程中流场的等涡量图如图14.

图14 翅翼下扑过程中流场的等涡量图(左列为柔性翼,右列为刚性翼)Fig.14 Iso-vorticity diagram of the flow field in the plunging process(flexible wing on the left and rigid wing on the right)
从0T到T/2 时刻,后缘涡在后缘远离边缘地方逆时针方向向翼面上方内卷,且向翼尖部位汇集.在汇集到翼尖后,上翼面涡达到最强时又逐渐向后缘脱落.此现象和鲍锋等[35]对于单自由度扑翼涡PIV 实验研究发现的规律较为一致.这是因为在扑动过程中翼尖的线速度最大,动压大导致翼尖处静压最小,使得涡向翼尖汇集,形成堆积涡从而又影响了翅翼展向上速度分布,在下扑达到最大速度时柔性翼与刚性翼的速度分布呈现了堆积涡形状如图15.
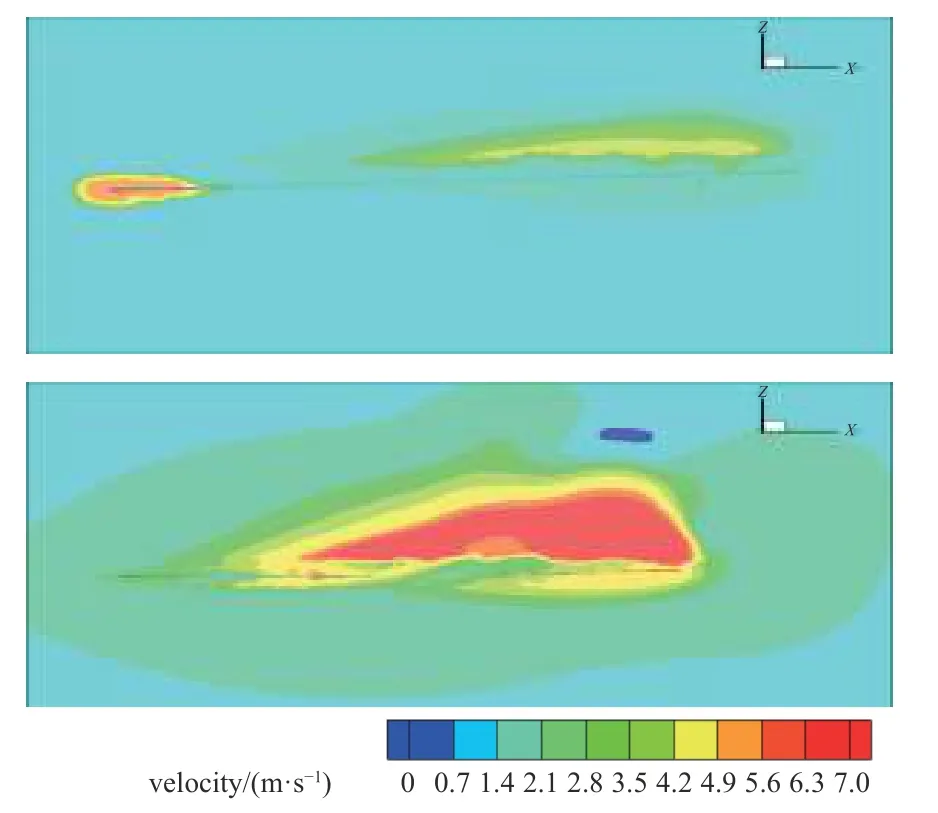
图15 T/4 时刻速度云图(上为刚性翼,下为柔性翼)Fig.15 Velocity cloud chart at T/4 (rigid wing up and flexible wing down)
从柔性翼流场的等涡量图可以看出:柔性翼堆积涡现象显著,从而导致上下翼面速度差增大,根据伯努利原理得出上下翼面的压强差增大,从而导致升力的明显增加,但是前缘涡脱落较快,这种现象对于升力具有消极的作用[33],导致柔性翼升力系数下降速度相比于刚性翼较快.
从刚性翼流场的等涡量图可以看出:在下扑过程中翼根部位始终有涡的存在,此现象和文献[36]对于三维刚性扑翼在单自由度下的二维截面涡量云图显示一致,由于在实际情况中蜻蜓身体的存在,因此在下扑时翼根处向上卷起的涡会给予躯体一个小的升力,但是对于翅翼的升力基本没有影响.
文献[37]对于飞蛾悬停实验的研究表明,扑翼飞行中大约有2/3 的升力取决于前缘涡.因此本文选取杨氏模量为10.4 GPa 均匀分布的柔性翼和刚性翼在升力系数峰值时刻,距离翼根不同位置处(6 个等距截面)的涡量云图来观察前缘涡.如图16 所示:柔性翼的前缘涡从翼根到翼尖逐渐扩散且扩散程度大于刚性翼,且前缘涡的强度在靠近翼根的三分之二位置以内(即靠近翼根的前4 个截面)明显强于刚性翼.
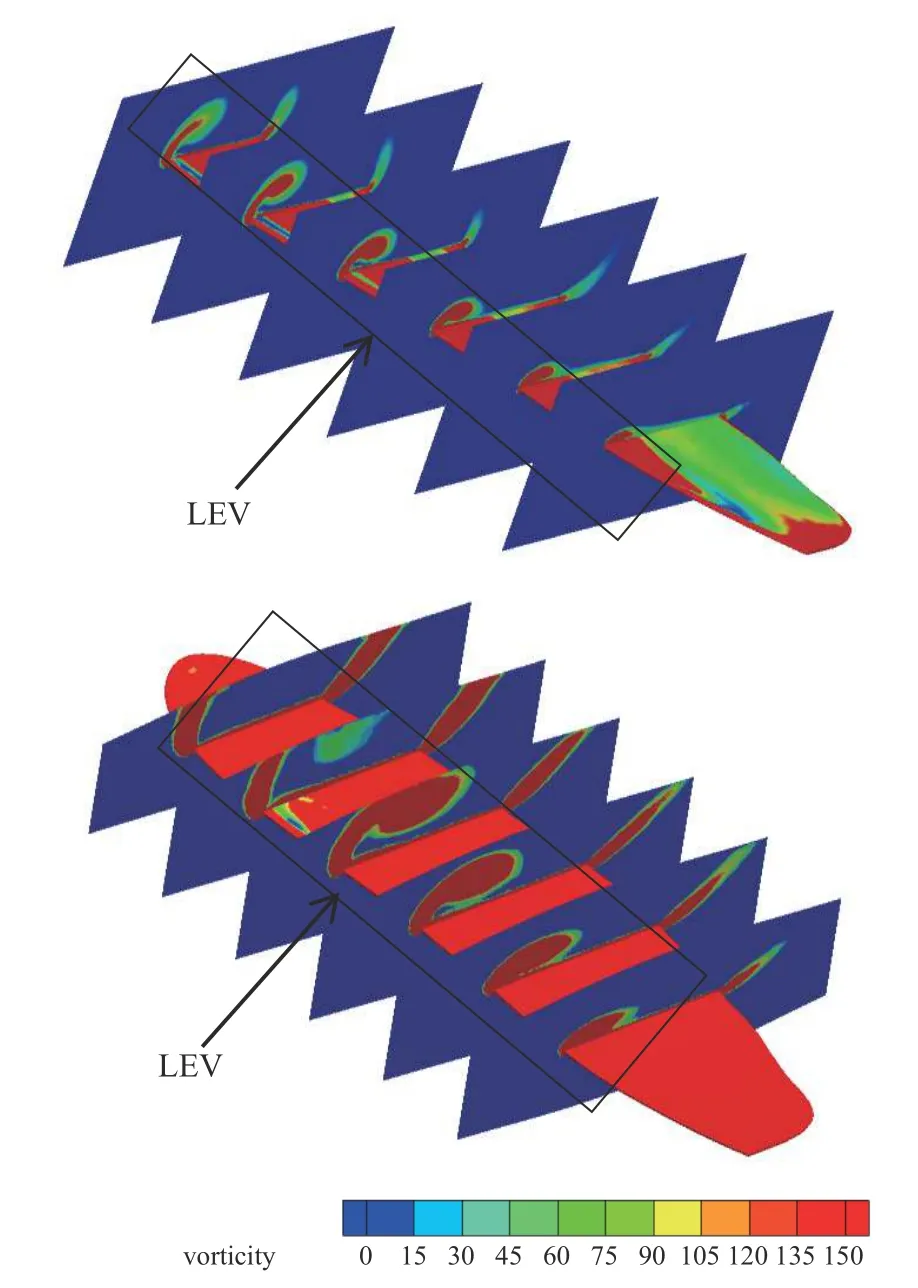
图16 T/4 时刻翅翼二维截面涡量云图(上为刚性翼,下为柔性翼)Fig.16 2D section vorticity cloud at T/4 (rigid wing up and flexible wing down)
根据扭转角做余弦函数的变化过程可以看出:沿展向柔性翼会发生弦向的周期性扭转振荡并改变了原有振荡的形式,这一振荡过程会使得前缘涡增强[38].因此导致在扑动速度最大时刻(即升力系数达到峰值时刻)做周期性扭转振荡的柔性翼的前缘涡要强于刚性翼,从而相比于刚性翼来说提高了升力系数峰值.
5.2 不同柔性分布下蜻蜓前翼的阻力系数
在均匀柔性分布的情况下,翅翼的阻力系数在不同杨氏模量的变化曲线如图17 所示.阻力系数曲线随着杨氏模量的增加:(1)最大阻力系数先减小后增加;(2)最大推力系数逐渐减小;(3)曲线的上下波动的程度逐渐减小,随后保持基本一样的波动幅度;(4)推力产生时长先小于刚性翼,随后逐渐增大.
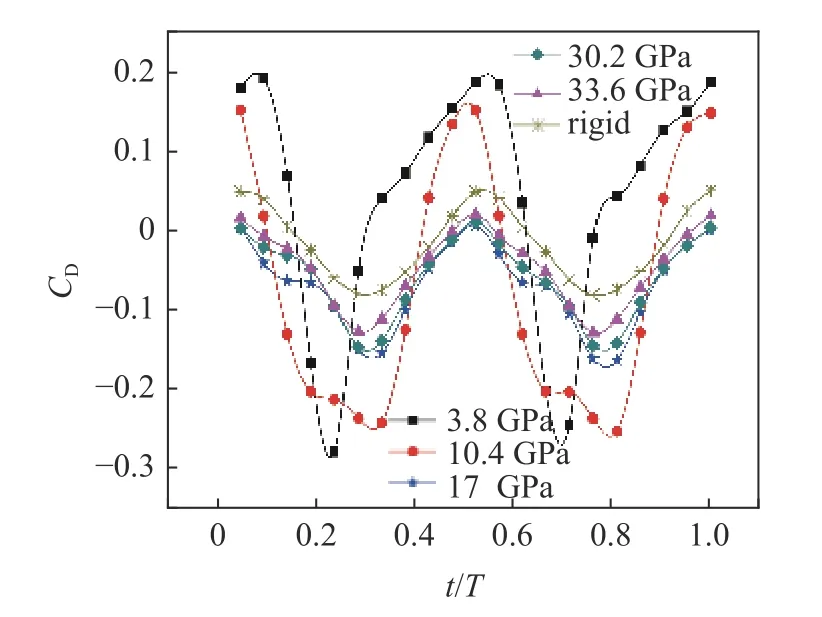
图17 均匀柔性分布下柔性翼的阻力系数Fig.17 Drag coefficient of flexible wing with uniform flexible distribution
总体来说,在一定刚度范围内,刚度的增加可以减小阻力,增加推力及产生推力时长(例如17 GPa,30.2 GPa 和33.6 GPa)这与高鹏聘等[39]对于柔性翼在不同刚度下的水动力特性试验研究发现的结果较为一致.
在变柔性分布情况下,翅翼的阻力系数如图18所示,相比于刚性翼来说:(1) 提高推力系数峰值;(2)明显增加推力在一个周期内的时间占比;(3)并不会较大增加阻力系数峰值.
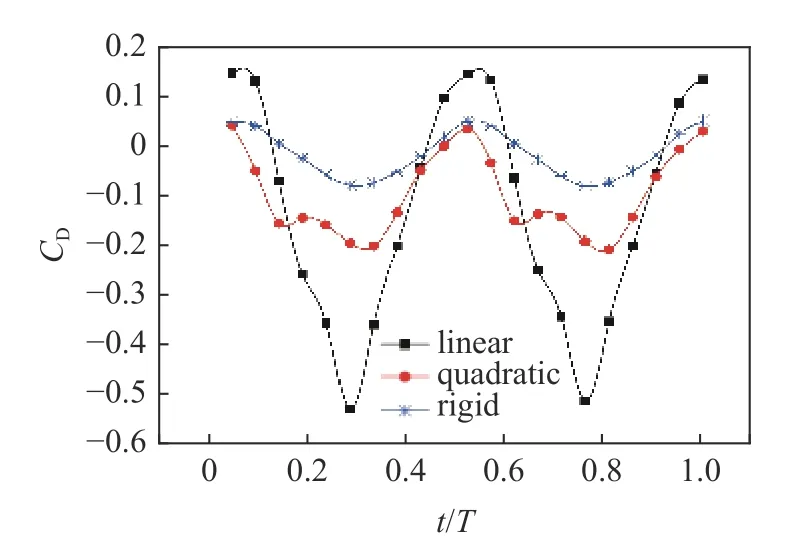
图18 变柔性分布下柔性翼的阻力系数Fig.18 Drag coefficient of flexible wing with variable flexibility distribution
相比于均匀柔性翼来说,既获得了3.8 GPa 均匀柔性分布时的高推力系数峰值,又综合了17 GPa 均匀柔性分布时的推力在一个周期内大的时间占比.因此表明刚柔并存的蜻蜓前翼在扑动时可以更好的提高推进效率.
为了探究阻力曲线变化中两次推力峰值产生的原因,将在推力系数峰值时刻对柔性翅翼尾涡运动进行分析.因为三维翅翼在扑动过程中,靠近翅翼后缘的第一对脱落涡距离翅翼最近且比后方的涡量大得多[35],也就对翅翼推力影响较大,所以本文主要研究靠近翅翼后缘的第一对脱落涡.虽然涡的结构为三维,但在一个近轴平面上,涡的旋转速度主要在流向平面[35],因此距离翼根36 mm的YZ平面上的脱落涡在一定程度上反映了整体涡系变化.
翅翼在下扑和上扑过程中规定涡量 ω 逆时针为正,顺时针为负,涡量最大(颜色最亮)为逆时针涡的涡心,涡量最小(颜色最深)为顺时针涡的涡心.
从图19 可以看出,在下扑过程中脱落的涡②与上一周期上扑过程中脱落的涡①在翅翼后缘形成一对反卡门涡街.从图20 看出,在上扑过程中脱落的涡③与下扑过程脱落的涡②再次形成一对反卡门涡街.在涡③完全脱落时涡①基本消散,这是因为涡在移动过程中的摩擦和碰撞导致涡量消散的较快[30].

图19 柔性翼下扑推力系数峰值时刻涡量云图Fig.19 Cloud diagram of vorticity at peak moment of thrust coefficient of flexible wing during upnward flapping

图20 柔性翼上扑推力系数峰值时刻涡量云图Fig.20 Cloud diagram of vorticity at peak moment of thrust coefficient of flexible wing during upnward flapping
因此每半个周期的脱落涡均可以和上半周期的脱落涡形成一对反卡门涡街来为蜻蜓前飞提供推力,这也导致了阻力系数曲线中会出现两次推力系数峰值.
从图21 中可以看出,在上扑推力系数峰值时刻刚性翼尾缘会产生上下两对反卡门涡街,此现象和文献[40]的仿蝌蚪刚性游动的尾迹出现上下两条反卡门涡街现象较为一致,但两对反卡门涡街的涡量强度较低,产生的推力相比于柔性翼来说较小.
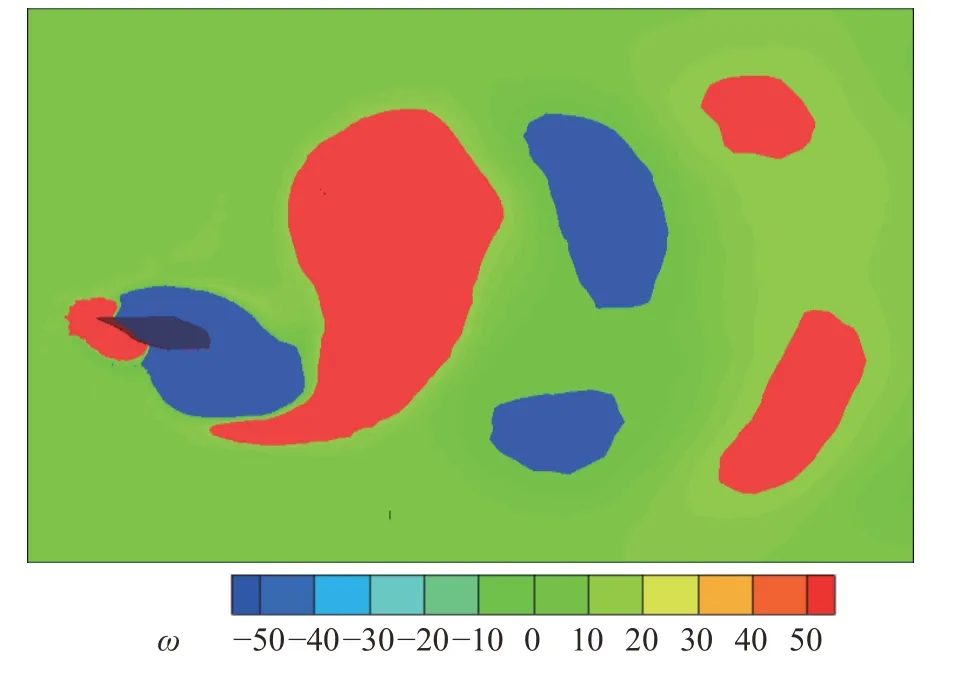
图21 刚性翼上扑推力系数峰值时刻涡量云图Fig.21 Cloud diagram of vorticity at peak moment of thrust coefficient of rigid wing during upnward flapping
从图22 和图23在T/4 时刻的流场带有速度显示的等涡量图可以看出来,无论翅翼是柔性还是刚性,均会出现连续的上下交替排列的后缘尾涡向来流方向发展且逐渐减弱.根据张志君等[41]对于5 种翼型(NACA0014,NACA2414,NACA4414,NACA8414,S1223-RTL)的仿生扑翼气动性能的研究,发现NACA8414 和S1223-RTL 产生了明显的后缘尾涡,有助于推力的产生.由此可得,因为柔性翼的后缘涡较强,即此刻(推力系数峰值时刻)产生的推力相较于刚性翼来说较大.

图22 T/4 时刻柔性翼流场的等涡量图Fig.22 Iso-vorticity diagram of flow field of flexible wing at T/4

图23 T/4 时刻刚性翼流场的等涡量图Fig.23 Iso-vorticity diagram of flow field of rigid wing at T/4
5.3 不同柔性分布下蜻蜓前翼获得的动量增量及加速度
根据动量定理,在一定时间内,外力作用在质点上的冲量,等于质点在此时间内动量的增量.积分形式表达式如下

通过Matlab 编程拟合并求解阻力曲线在一个周期内的积分,积分为负时表示推力作用在翅翼上的冲量大于阻力作用,获得的动量增量为负,加速度方向和前飞方向一致,加速度为正.翅翼获得的动量增量以及加速度表达式如下
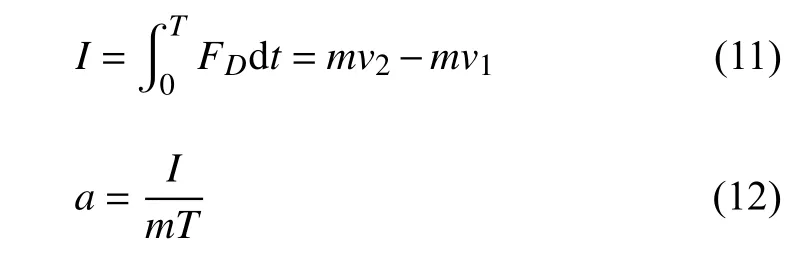
式中,FD为阻力;T为扑动周期;m代表蜻蜓前翼质量.
根据动量定理和加速度表达式计算得出在不同杨氏模量分布下动量变化和加速度变化的结果如下表2 所示.(1)均匀柔性分布时,随着杨氏模量的增加动量增量先增加后减小,加速度也先增加后减小;(2)变柔性分布的翅翼相比于刚性翼来说,显著提高了动量增量以及获得了较高的加速度;(3)在翅翼做单自由度的扑动运动情况下,线性函数变柔性分布时可以为蜻蜓提供较大的前飞动量增量以及加速度.
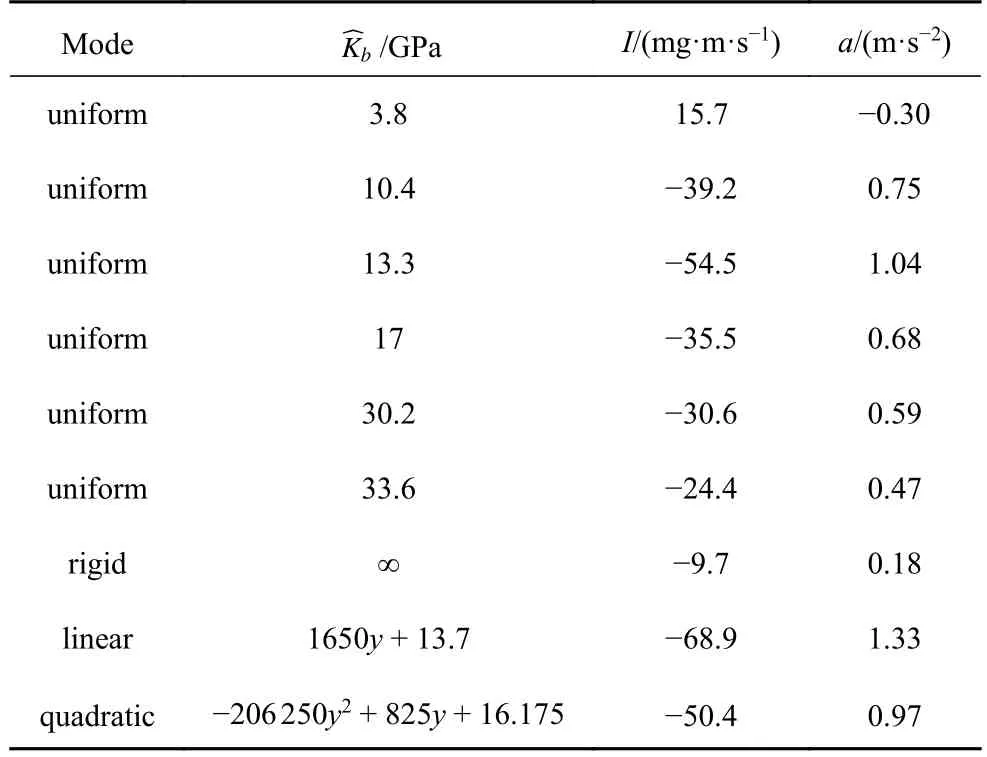
表2 蜻蜓前翼周期内的动量增量及加速度Table 2 Momentum increment and acceleration in the period of dragonfly's forewing
5.4 不同柔性分布下蜻蜓前翼在一个周期内时均推力系数
一个周期内的时均推力系数表达式如下

通过Matlab 编程计算得出在不同杨氏模量分布下的时均推力系数如表3 所示.其中时均阻力系数为负值时表示一个周期产生的净阻力为推力反之为阻力.
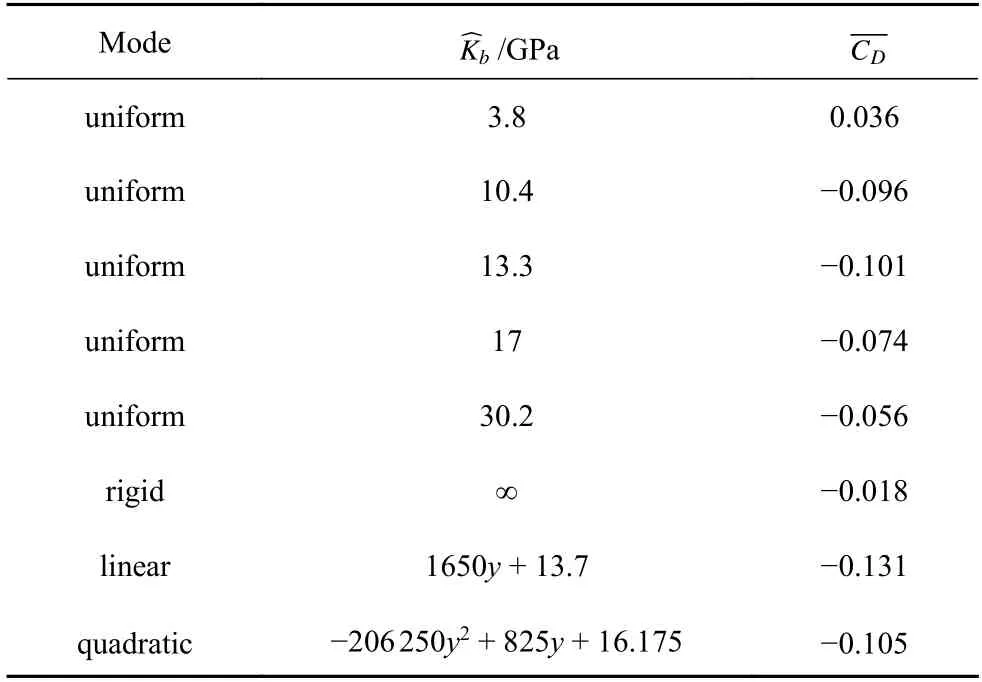
表3 蜻蜓前翼不同柔性下的时均推力系数Table 3 Average thrust coefficient of dragonfly forewing under different flexibility
在均匀柔性分布时,杨氏模量较小时,并不会帮助蜻蜓获得更好的推力,反而增加了阻力.随着杨氏模量的增加,时均推力系数先增加后减小.这种变化规律与钱靖等[42]对于翼型后缘薄板不同杨氏模量下产生的平均推力系数仿真结果规律一致.
在变柔性分布时,时均推力系数相对于刚性翼来说得到了显著提高.再次证明了刚柔并存的蜻蜓前翼使得蜻蜓获得更好的气动性能.
6 结论
本文基于流固耦合探究了两种柔性分布方式对于蜻蜓前翼气动性能的影响.
均匀柔性分布时,杨氏模量较小时,翅翼翼尖的变形趋势会与杨氏模量较大的均匀柔性分布相反且导致升阻力系数变化趋势滞后刚性翼半周期.
两种柔性分布方式下的柔性翼相比于刚性翼来说均可以显著提高升力系数峰值.其一,由于柔性翼在扑动过程中产生的堆积涡使得上下翼面压差增大.其二,由于柔性翼扑动过程中会产生扭转振荡使得前缘涡增强.
两种柔性分布方式下的柔性翼相比于刚性翼来说均可以显著提高推力系数峰值.其一,柔性翼扑动在后缘产生的反卡门涡街的涡量强度要强于刚性翼.其二,柔性翼较强的尾缘涡有助于推力的产生.
在一个周期内,柔性翼在均匀柔性分布下,随着杨氏模量的增加,给予蜻蜓的动量增量增量先增加后减小,加速度先为减速后为加速且加速大小先增加后减小.在变柔性分布下,柔性翼相对于刚性翼来说,给予蜻蜓的动量增量较大,可以提供给蜻蜓较大的前飞加速度.
时均推力系数在均匀柔性分布下,随着杨氏模量的增加,先增加后减小(其中杨氏模量较小时的时均推力系数体现为阻力).在变柔性分布下,时均推力系数相比于刚性翼显著增大,其中线性函数分布时,时均推力系数显著提高.
