复杂大气入流下海上风机力学特性研究1)

2022-06-13徐顺赵伟文万德成

力学学报 2022年4期

徐顺赵伟文万德成

(上海交通大学船舶海洋与建筑工程学院,船海计算水动力学研究中心(CMHL),上海 200240)

引言

近年来,传统化石能源的不可再生性以及对环境造成的污染,使其难以满足当今社会对能源的巨大需求.风能由于其无污染、可再生及储量大等特点逐渐成为最具发展潜力的新能源之一[1].2021 年全球风能报告指出[2],2020 年新增装机容量高达93 GW,同比增长53%.风能技术的不断进步,促使风机尺寸逐渐向大型化发展,并导致大气边界层(atmospheric boundary layer,ABL)复杂来流对风机的运行性能、疲劳载荷等方面产生恶劣影响.因此,研究大气边界层内风机的运行性能和力学特性具有重要意义.

目前,生成满足大气边界层复杂来流统计特性的方法主要有两种[3]:人工合成和域前模拟.人工合成的基本思想是在入口平面处基于严格的数学推导给出入流风速的计算公式.宁旭[4]采用谐波合成法生成了符合高雷诺数湍流能谱分布的随机风速序列,并将其应用于风机数值模拟.Huang等[5]提出了“DSRFG”方法,该方法生成的脉动风速场严格满足连续性条件且能够并行计算生成不同空间位置的风速时程.Castro 和 Paz[6]在“DSRFG”方法的基础上,通过引入时间尺度参数考虑了脉动风速场的时间相关性.但是,人工合成法给定的风速不能严格满足NS 方程,需沿下游发展一段距离才能获得符合统计特性的大气湍流风场.Xie等[7]对传统2D 涡方法进行了参数化研究,提出了改进的2D 涡方法,将符合湍流统计特性的下游自适应距离由原来的5h减小到3h(h为计算域的高度).

域前模拟的基本做法是预先生成一个符合大气湍流统计特性的风场,并将其作为计算区域的入口边界条件.在域前模拟中,生成大气湍流风场的方法主要有两种:利用湍流激发装置以及依靠表面粗糙度.在实验中经常利用湍流激发装置(如粗糙元、网格板等)来促使大气湍流风场的生成[8-10],后来有部分学者将其应用于数值模拟中.Phuc等[11]利用尖劈和粗糙元构建了数值风洞,其数值模拟出的湍流风场统计特性与实验值符合良好.周桐等[12]利用尖劈和粗糙元等湍流激发装置数值模拟了大气边界层入口湍流,与“CDRFG”方法对比,该方法生成的流场结构更加合理.但是,该方法模拟出的湍流风场特性高度依赖于湍流激发装置附近的网格分辨率,且激发装置与流场相互作用机理机制尚不明确.

另一种域前模拟方法是直接依靠计算域底部的粗糙度,无需进行复杂的网格划分,直接长时间大范围数值模拟出大气边界层湍流风场,如美国国家可再生能源实验室研发的风机气动性能数值计算软件“SOWFA”便基于此方法生成复杂大气入流[13].Lee等[14]研究了不同表面粗糙度和稳定性的大气入流及风机尾流对下游风机疲劳载荷的影响,结果表明表面粗糙度和上游风机尾流对风机疲劳载荷影响显著.Ning 和Wan[15]基于LES 结合致动线模型,研究了不同大气稳定性下尾流弯曲效应及其对下游风机气动性能的影响.白鹤鸣等[16]基于“SOWFA”软件,对对流大气边界层下错列排布三风机进行数值模拟,发现垂向错列可以有效提升后排风机的功率,且不会恶化其气动性能.李德顺等[17]利用LES 结合致动线模型的方法对一台处于中性大气入流下的外场试验机组进行了叶根载荷分析,发现叶根挥舞载荷对大气中的湍流结构响应明显.Johlas等[18-19]通过结合“SOWFA”和“OpenFAST”[20],对大气复杂入流下浮式风机的尾流场进行了分析,并对比了不同浮式支撑平台对风机尾流场和平台六自由度运动的影响.

以上研究中,大都采用域前模拟中的依靠地表粗糙度的方式来生成风机的大气复杂入流,但其中却少有文献重点关注风机的力学特性响应.因此,本文采用域前模拟的方法,通过定义典型海面粗糙度,直接长时间大范围数值模拟真实环境下中性大气边界层复杂入流.并结合LES 和致动线模型,对中性大气复杂入流下的海上固定式风机进行数值模拟,并以均匀入流计算结果作为参考基准,定量分析大气复杂入流对风机气动性能和叶根载荷的影响.

1 数值方法

1.1 致动线模型

风机叶片利用致动线模型进行模拟,该方法无需求解叶片表面边界层,能大幅降低计算成本并获得较为精确的结果.其最早由Sørensen 和Shen[21]提出,基本思想是利用致动线上的致动点代表沿着径向离散化的风机叶片,然后基于叶素理论计算致动点的体积力,并将其反作用于流场以体现风机叶片对流场的作用.致动点上的体积力可采用下式计算

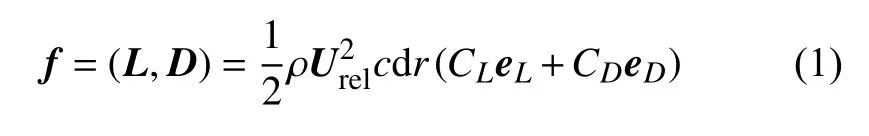
式中,L和D分别代表叶片半径r处叶素的升力和阻力,ρ 为空气密度,Urel为相对入流风速,c为叶片半径r处二维翼型的弦长,dr为叶素的宽度,CL和CD分别为升力系数和阻力系数,可根据攻角确定,eL和eD为升力和阻力方向的单位矢量.

图1 显示了叶片半径处二维翼型的速度矢量,其中相对入流风速可由下式确定

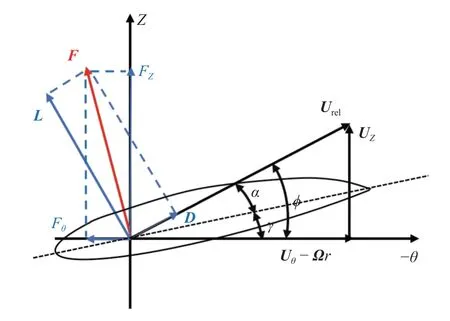
图1 二维翼型的速度矢量Fig.1 Velocity vectors of two-dimensional airfoil

式中,Uz和Uθ分别为入流风速的轴向速度和切向速度,Ω 为转子角速度.

另外,若直接将致动点上的体积力作用于流场,会造成数值奇异性,在此采用高斯核函数进行体积力光顺投影,光顺后的体积力表达式如下

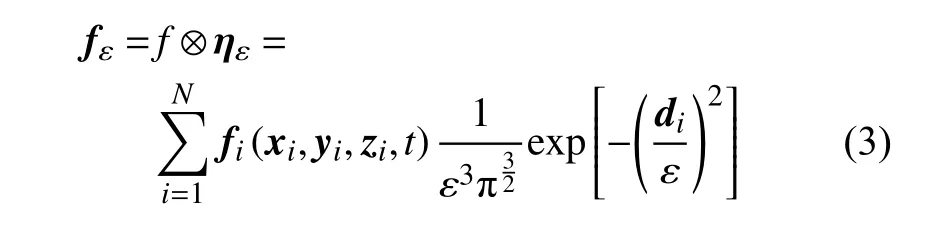
式中,N为叶片上致动点的数目,(xi,yi,zi) 表示第i个致动点的位置,di为致动点距离投影点的距离,ε 代表投影的宽度,本文取 ε ≈2Δx[22],Δx为叶片附近的网格尺寸.

1.2 控制方程

本文采用大涡模拟方法,对中性复杂大气入流下的海上固定式风机进行数值模拟,空间过滤后的流场的控制方程如下

式中,动量方程右端第一项为修正压力梯度项,第二项为背景压力梯度项,用以克服计算域底部表面粗糙度并驱动大气湍流的生成,第三项为考虑地球自转的科氏力项,第四项代表温度引起的浮力项,第五项为流体应力张量项,采用“Smagorinsky”亚格子模型封闭,第六项为风机叶片体积力源项,由致动线模型计算得出,在域前模拟阶段忽略此项.另外,还需要求解位温输运方程以获得位温场

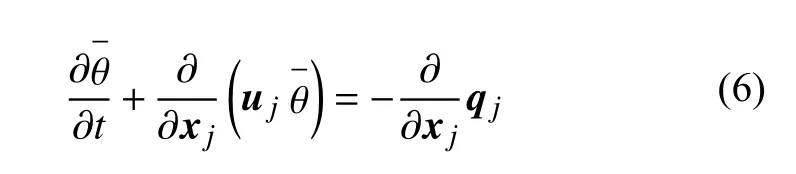
式中,热通量qj由下式计算

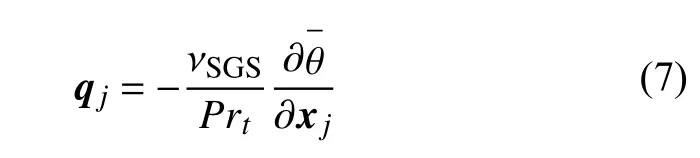
式中,Prt为普朗特数,在中性和对流大气边界层中取 1/3,关于控制方程更详细的说明可查阅参考文献[23].对于均匀入流下的风机,其流场的控制方程未考虑科氏力项和温度项的影响,也不需要背景压力梯度驱动流体流动,在此不再重复赘述.

1.3 局部坐标系

在本文的结果分析中,需要对风机转子气动力和力矩以及叶片根部的力和力矩进行结果分析,两者所采用的坐标系不同,在此进行简要说明.

风机转子气动力和力矩采用的是轮毂局部坐标系,如图2(a)所示,其坐标原点为转子轴与旋转平面的交点,x轴为沿着轮毂中心线指向下游方向,z轴垂直于轮毂中心线并与叶片具有相同的方位角,y轴根据右手螺旋定则确定.

图2 局部坐标系示意图Fig.2 Local coordinate systems

叶片根部的力和力矩基于叶片局部坐标系,如图2(b)所示,其中i代表叶片编号.y轴平行于弦线并指向叶片后缘,z轴为沿着桨距轴指向叶尖,x轴根据右手螺旋定则确定.另外,两个局部坐标系均会随着叶片旋转.

2 算例设置

2.1 风力机参数

本文所采用的研究对象为美国国家可再生能源实验室(National Renewable Energy Laboratory,NREL)开发的5 MW 风机,其是一种传统迎风向可变桨距和转速的3 叶片风力机.该风机的额定风速为 1 1.4 m/s,对应的额定功率和额定转速分别为5 MW 和12.1 r/min,该风机的主要参数如下表1 所示,关于该风机更详细的数据可参考文献[24].

表1 NREL 5 MW 风机主要参数Table 1 Main parameters of NREL 5 MW wind turbine

2.2 大气入流算例设置

考虑真实复杂大气入流的海上固定式风机数值模拟需要分两阶段进行:域前模拟和主模拟.在域前模拟阶段,需要长时间大范围的依靠底面粗糙度来生成真实的大气湍流风场.如图3 所示,计算域的四周侧壁均采用周期性边界条件,以达到通过减小计算域尺寸降低计算量的目的,计算域顶部设置为滑移边界条件,底面采用“Moeng”壁面模型[25],表面粗糙度设置为0.001,对应典型低粗糙度的海面情况.计算域的长度、宽度和高度分别设置为3000 m×3000 m×1000 m,三个方向的网格分辨率为10 m×10 m×10 m,对应的网格数量为900 万.轮毂高度处的风速设置为风机的额定风速 1 1.4 m/s,入流风向设置为240°(西南方向入流)以避免在周期性边界条件中同一高度处的涡结构几乎同时到达下游边界时又同时传入上游边界时“卡死”现象的出现.

图3 域前模拟计算域及边界条件(单位:km)Fig.3 Calculation region and boundary conditions of precursor simulation (unit:km)

对于初始位温的设置,从底部至700 m 高度设置300 K 均匀分布,700 m 至800 m 高度设置逆温反转层,其中的温度线性增长到308 K,800 m 至1000 m 高度的温度以 0 .003 K/m 的速率线性增长.为了使生成的大气湍流达到准平衡态,域前模拟阶段的计算时间为19 000 s,计算步长为0.4 s,保留最后1000 s 的计算数据作为主模拟阶段的输入.

主模拟阶段的计算域和背景网格的分辨率与域前模拟阶段相同,但北面和东面侧壁边界修改为零梯度边界条件以防止下游风机尾流循环进入上游边界,如图4 所示.另外,为了更加精确的捕捉风机尾流区域的流场细节,对风机附近的区域进行了二级网格加密,加密后风机附近的网格尺寸为2.5 m×2.5 m×2.5 m,总网格数量约为1400 万.时间步长的设置需要满足CFL 收敛性条件

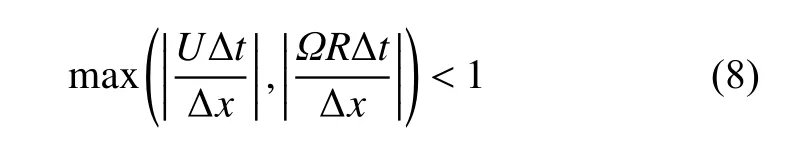
图4 主模拟计算域布置 (单位:m)Fig.4 Successor simulation calculation region (unit:m)

式中,U=11.4 m/s,为轮毂高度入流风速;R=63 m,为转子半径;Ω=12.1 r/min,为入流风速下的转子转速;Δx=2.5 m,为风机叶片附近的网格分辨率.代入上式,可得 Δt＜0.031 s,因此,本文的时间步长设置为0.02 s.计算时长为1000 s,对应于域前模拟阶段的流场数据保存时间,并利用最后350 s 的计算数据进行结果分析.本课题组在风机数值模拟方向具有扎实的研究基础,关于风机附近网格划分策略的详细细节可参考文献[26-28].

2.3 均匀入流算例设置

如图5 所示,均匀入流算例计算域的长度、宽度和高度分别设置为 1 0D×3D×3D,D为转子直径126 m.风机距离上游边界为 2D,同样,与主模拟做法相一致,背景网格的尺寸为 1 0 m×10 m×10 m,并对风机叶片附近区域采取二级网格加密策略,加密后的网格尺寸为 2 .5 m×2.5 m×2.5 m,网格数量约为320 万.另外,上游边界为速度入口边界条件,对应于11.4 m/s 的均匀入流,入流风向为270°(西侧方向入流),下游边界为自由流出边界条件,四周壁面为周期性边界条件.时间步长为0.02 s,计算时间为400 s,并利用最后350 s 的计算数据进行结果分析.

图5 均匀入流计算域布置Fig.5 Calculation region of uniform inflow

3 结果分析

3.1 气动功率

图6 显示了计算结果最后350 s 中性大气入流和均匀入流下海上固定式风机的功率时历曲线.可以看出,均匀入流下的转子气动功率输出较为稳定,但大气复杂入流下转子功率输出变化十分复杂,转子功率在t=25 s 附近开始存在一个较低值,且持续时间超过50 s,这是由大气复杂入流中的大尺度低速气流导致.另外,随着时间的增加,气动功率值迅速增加至6 MW 附近,在t=90 s 附近又存在较大的下降梯度,随后又逐渐增加,并在均匀入流风机的气动功率值附近振荡.

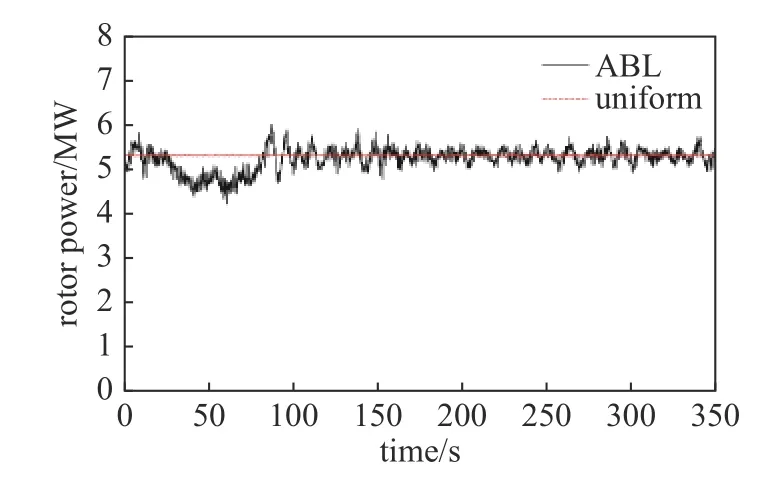
图6 功率对比Fig.6 Comparison of rotor power

在数据统计特性方面,分别统计了气动功率的最大值、最小值、平均值、均方根和标准差,如表2所示.可以看出,两种工况的气动功率均方根值差异不大,分别为5.22 MW 和5.30 MW,因为气动功率的均方根值主要由平均风速决定,两种计算工况的平均风速均在11.4 m/s 附近.但是,大气入流中的复杂湍流会引起气动功率振荡幅值的极大增加,进而引起标准差的增加,其值约为均匀入流气动功率标准差的4 倍.

表2 气动功率统计值Table 2 Aerodynamic power statistics

3.2 轴向推力和偏航力矩

轴向推力和偏航力矩属于风机转子的气动力和力矩,其局部坐标系为轮毂坐标系,其中轴向推力沿轮毂坐标系x轴,偏航力矩绕z轴.图7(a) 和图7(b)分别显示了大气入流和均匀入流两种工况下风机转子的轴向推力和偏航力矩对比曲线.与气动功率输出类似,均匀入流下风机的轴向推力稳定在600 kN 附近,而复杂大气入流下的轴向推力输出无论是变化幅度还是变化梯度均较大,这同样归因于复杂大气入流下的大尺度湍流来流.

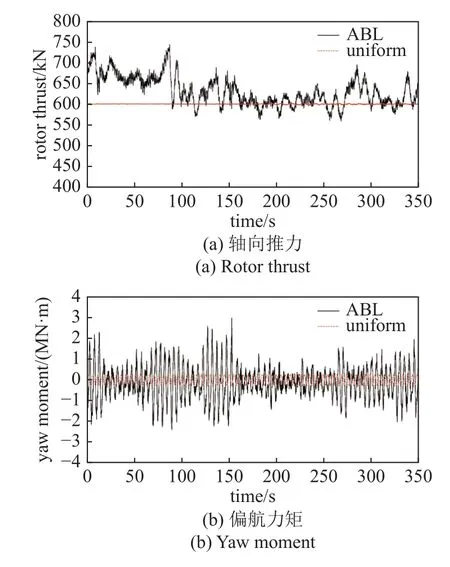
图7 轴向推力和偏航力矩对比Fig.7 Comparisons of rotor thrust and yaw moment

当风机转子的其中两个叶片位于塔架同一侧时会导致盘面受力的横向不对称性,并由此产生偏航力矩.因此,即便在均匀入流下,风机偏航力矩也会随叶片旋转作周期性变化,变化周期对应于叶片旋转周期.然而,复杂大气入流下的流场扰动会使得风机的偏航力矩随时间呈现明显区别于均匀入流工况的复杂变化,明显加剧偏航力矩的周期性变化幅度,并显著增加其均方根值,如图7(b)所示.因此,在风机偏航优化控制中需重点关注复杂大气入流带来的不利影响[29].

表3 显示了两种入流工况下轴向推力和偏航力矩的统计值.虽然轴向推力的均方根值差异不大,但复杂大气入流下的轴向推力标准差与均匀入流相比增大了约53 倍.另外,针对偏航力矩,复杂大气入流的流场扰动极大的增加了其幅值,偏航力矩的最大值和最小值分别增加到均匀入流的10 倍和8 倍,并导致均方根和标准差的比值为均匀入流的4.3 倍,相关文献[4]也表明复杂入流下各类结构载荷的标准差值较均匀入流时均有大幅增加.

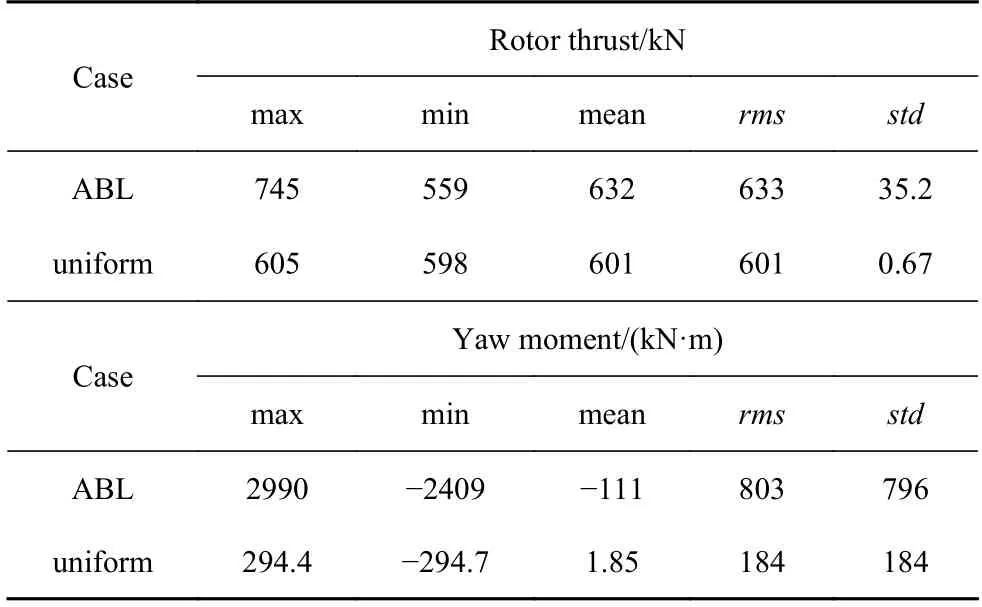
表3 轴向推力和偏航力矩统计值Table 3 Statistics of rotor thrust and yaw moment

3.3 摆振剪力和弯矩

摆振剪力和弯矩的参考坐标系为风机叶片局部坐标系,其中摆振剪力沿x轴,摆振弯矩绕y轴.图8分别显示了摆振剪力和弯矩的对比曲线由图8(a)可以看出,均匀入流下叶根部位的摆振剪力随叶片旋转作周期性变化,变化周期对应于叶片旋转周期.另外,大气入流下的摆振剪力也近似作周期性变化,但是,由于复杂大气入流下的高强度湍流结构及速度沿垂向分布的不均匀性,导致摆振剪力的变化幅度较为剧烈且随机.摆振弯矩主要由摆振剪力引起,两者的变化趋势基本一致,在此不再重复赘述.

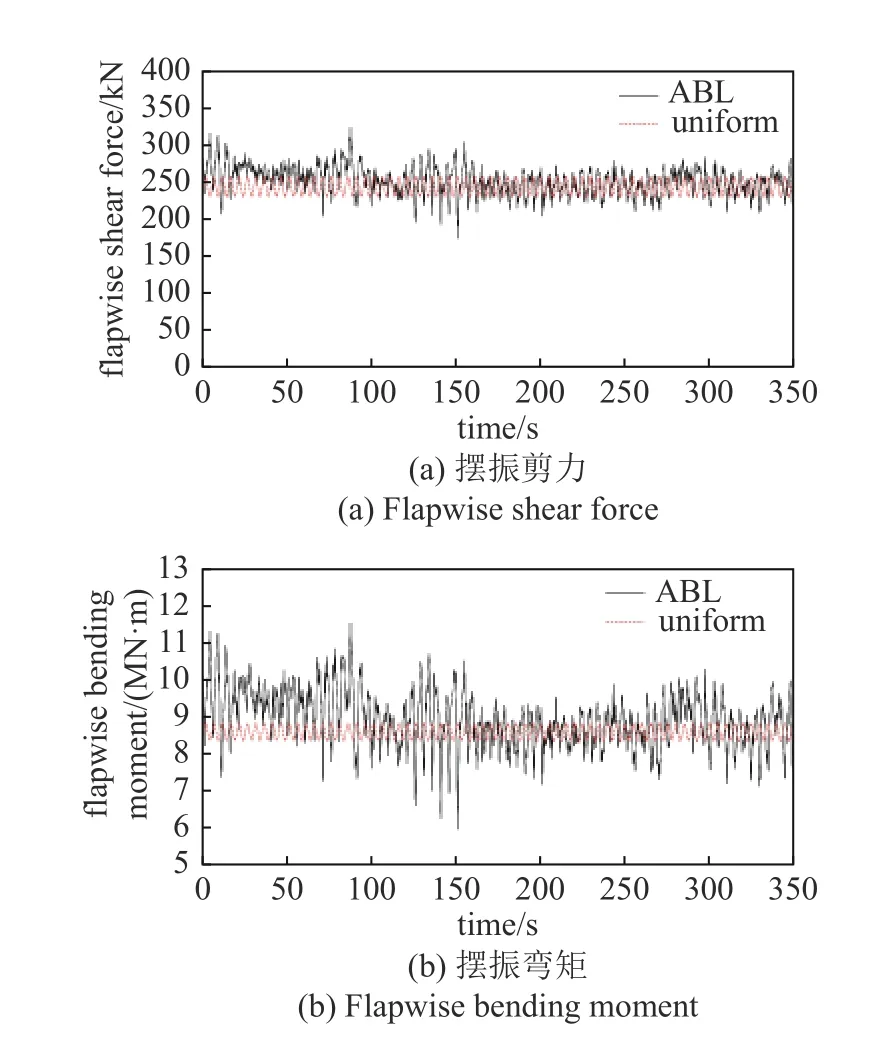
图8 摆振剪力和弯矩对比Fig.8 Comparisons of flapwise shear force and bending moment

表4 给出了摆振剪力和弯矩的统计值,可以看出,复杂大气入流和均匀入流工况下摆振剪力和弯矩的均方根值差异不大.但是,由于复杂大气入流的流向风速在垂向上存在速度梯度,当风机叶片旋转至轮毂平面上方时,摆振剪力和弯矩值较均匀入流增大;反之,较均匀入流减小,这导致了摆振剪力和弯矩标准差值的显著增加.

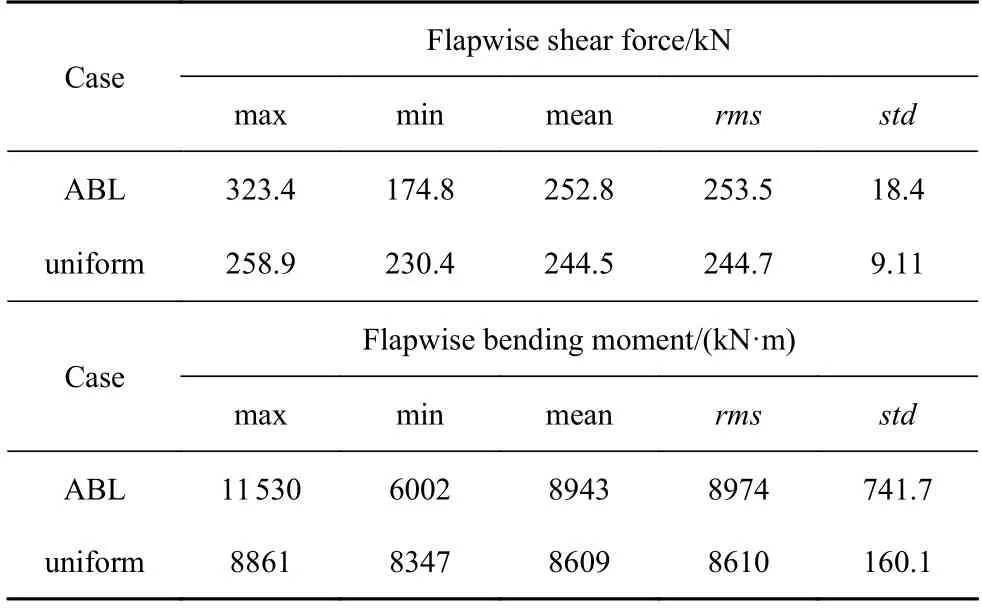
表4 摆振剪力和弯矩统计值Table 4 Statistics of flapwise shear force and bending moment

3.4 速度云图

图9 显示了复杂大气入流下某时刻的流场速度云图.由图9(a)可以看出,轮毂高度处的来流速度同时存在大尺度的高速和低速的气流团结构,并且在风轮旋转平面处存在明显的不对称性,使得偏航力矩振荡幅值急剧增加.由于风机吸收了入流风的能量,导致风机盘面后方的尾流区域存在明显的速度损失.本文并未对轮毂进行建模,因此在轮毂中心处存在一条狭长的高速气流,该气流随着向下游传播迅速和低速风机尾流相互掺混.另外,尾流膨胀和蜿蜒效应也清晰可见.

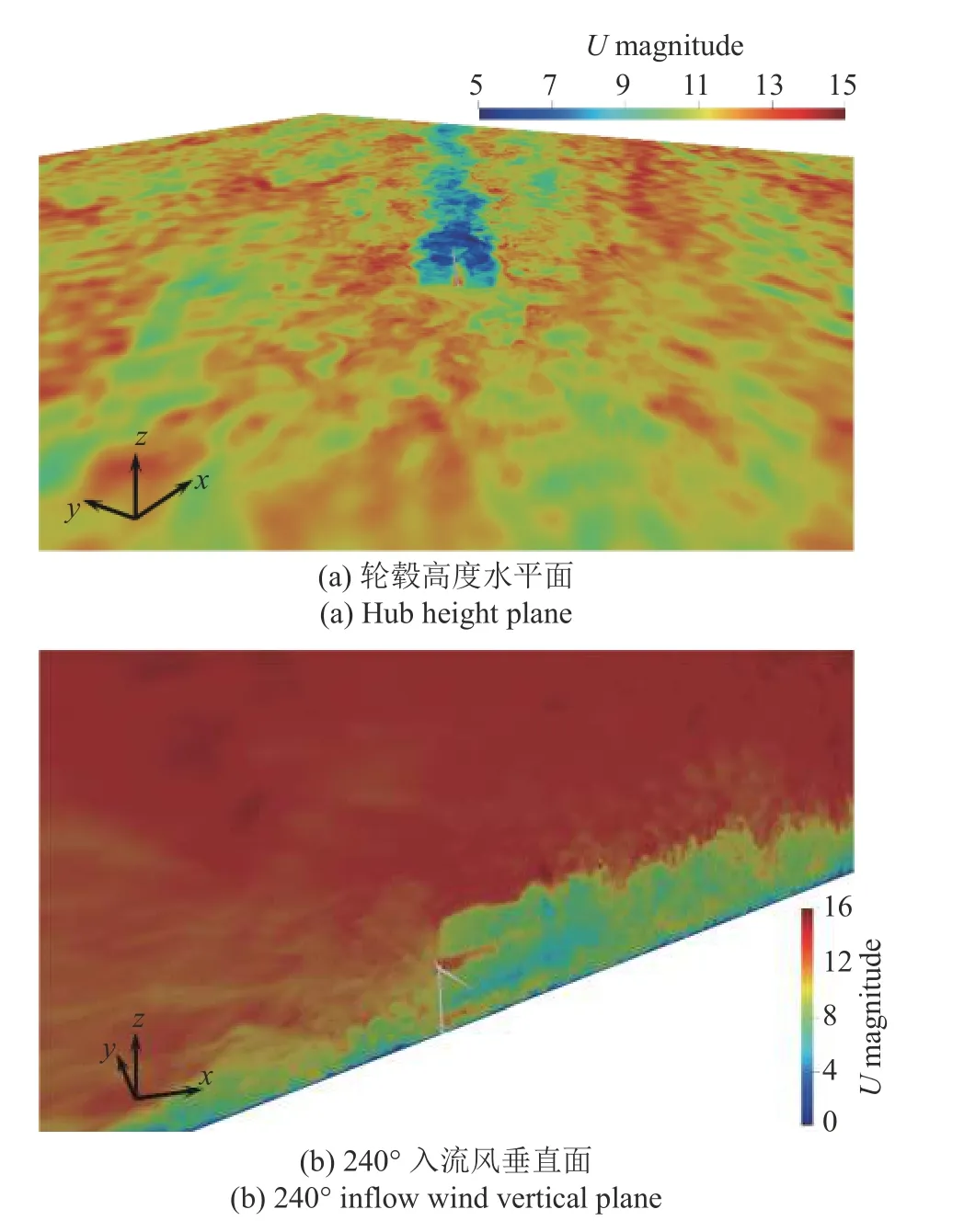
图9 瞬时速度尾流场Fig.9 Instantaneous velocity wake field

图9(b)展示的是240°入流风垂直面的瞬时尾流速度云图,可以看出,由于海面的阻滞作用,在靠近计算域底部高度处存在着大尺度低速气流结构.另外,在轮毂高度附近存在大尺度低速羽流结构,其与计算域底部的大尺度低速气流团相互作用会显著增加叶片摆振剪力和弯矩的振荡幅值.在风轮旋转平面下游,可以明显看出风机尾流与外部大气之间的掺混作用.但由于海面低粗糙度的作用,使得中性复杂大气入流的环境湍流强度较高地表粗糙度时低,导致风机尾流速度随下游流向距离恢复较慢.

3.5 尾涡结构

第三代涡识别方法能够合理回答涡的六大要素问题,并定量化表示涡的特性.因此,本文采用第三代“Liutex”涡识别方法[30],对中性复杂大气入流下海上固定式风机的尾涡结构进行可视化识别.根据图10 可以看出,由于中性大气入流的复杂湍流场,导致在风机上游就已形成多尺度湍流涡结构.风机叶片的旋转会诱导出清晰可见的叶尖涡,该叶尖涡与复杂大气入流涡结构的相互作用引起叶尖涡的迅速破碎,并与小尺度环境涡结构相互掺混向下游传播.另外,风机尾涡的膨胀效应也清晰可见.